「量子もつれ」って何？

ベルの不等式とアスペの実験

　2022年のノーベル物理学賞はアスペ(Aspect)、クラウザー(Clauser)、ツァイリンガー(Zeilinger)に送られました。

　ノーベル賞のweb→The Nobel Prize in Physics 2022

　量子力学の（ある意味非常識な）性質を証明する実験に対してです。この講演では、これらの実験とその基礎である「ベルの不等式」について話していきます。

カーソルまたは▶などのクリックで前後に進むことができます。

$\def\ket#1{\left|#1\right>}\def\mtx#1#2{\left(\begin{array}{#1}#2\end{array}\right)}$

量子力学の「非常識」

最初に、

「量子力学のどこに驚いて欲しいか」

を話しておこう。

我々が感知できる世界は、いわば「世界の切り口」だけです。

実験や観測は、世界の一部を見せてくれるだけです。特に量子力学は「見えている切り口」が「世界のほんの一部」だということを思い知らせてくれます。

　さらにこの世界は、「決定論的」ではないです。

どういうこと？？
それを今から説明していきましょう。

量子力学の前に古典力学

現代において「古典力学」とは「量子力学ではない」という意味です

（「現在はやってない」という意味ではない）

「古典力学」は、割と「常識的な世界」です。その常識的な世界との量子力学的世界の差を知るための簡単な例として、棒磁石を古典的に、次に量子力学的に考えてみましょう。

古典的な「磁石の向き」はアプリ「磁石を回す」でわかるように、２つの角度が「変数」になってます。

しかし、量子力学的な状態に関してはそうではないのです。そのことを示す実験をまず紹介しましょう。

この講演で話す実験は、（説明の都合上）実際と違う点があります。

シュテルン・ゲルラッハの実験

↑長いので、以下「シュテルン・ゲルラッハ」→「SG」と略す。

銀の原子が不均一な磁場中でどう動くかを見るという実験です。（なお、実際の実験は複雑なので、かなり単純化して話をします）
不均一な磁場中で、磁石は力を受けます。
どういう実験なのかはアプリで説明。

「不均一」がなぜ必要なの？と思った人は▼を見ること。
　　　　

　均一な磁場中では、N極に働く力とS極に働く力は同じ大きさで向きが逆なので、全体として働く力は0です。

　　　　

　不均一な磁場中では、N極に働く力とS極に働く力の大きさが変わるので全体に力が働く。

実際の実験の結果

　Stanford Encyclopedia of PhilosophyのStern-Gerlach Experimentのページ←画像あり。

ビームは「二つ」に分かれる！

　銀原子という「微小な磁石」が古典的な「磁石」なら、結果は連続的になるはず。

↑こうなるべきじゃね？

いや、むしろ↑こうなるべきじゃね？

磁石は回らないの？と思った人は▼

磁石は回らないの？

　磁石がだろうがだろうが、あるいはだろうがだろうが、上向きの磁場がかかっているなら全部になるのでは？

と思うのはごもっともなのだが、この回転は起こってない。もし回るのなら、全部同じ方向を向きそうだが、実験結果は二つの結果を示しているのである。
実際に何が起こるかを計算してみると▼

　実は原子が磁石になっているのは（広い意味で）「自転運動」をしているからである。自転している物体に回すような力を加えると、回転軸が変わる（歳差運動）。

のように力が加わると のように回る。
よって、単純に磁場を掛けるだけでは、原子の向きを↑に揃えることはできない。

銀原子の状態は「量子化」されている。

　この実験の銀原子の状態は「磁石が上向きの状態」と「磁石が下向きの状態」の二つがある。中途半端な状態はない。

状態が連続的（アナログ）なものではなく、離散的（デジタル）なものになってしまうことを「量子化」されている、と言います。
ややこしいんですが、「量子力学では状態が量子化されている」というのは間違いで、量子力学だけど状態が連続的な場合もあります。

なんか変だな？

ここで「ちょっと待って、なんか変だよ！？」となって欲しい。

変だと思ったかな？

当然の疑問１：とはないの？

当然の疑問２：磁場の方向変えたらどうなるの？

磁場の掛け方変えたら？

さっきの向きを上下方向として、進行方向から見て左右方向に磁場を掛けたら？

上下方向→ 左右方向→

予想してみてください。

  1. 銀原子は上と下を向いているから、左右方向には力を受けないはず。だから、分離しないだろう。
  2. 今度は、左右方向に二つ（奥側と手前側）に別れるだろう。
  3. その他（自由回答）
結果は次のページ

結果

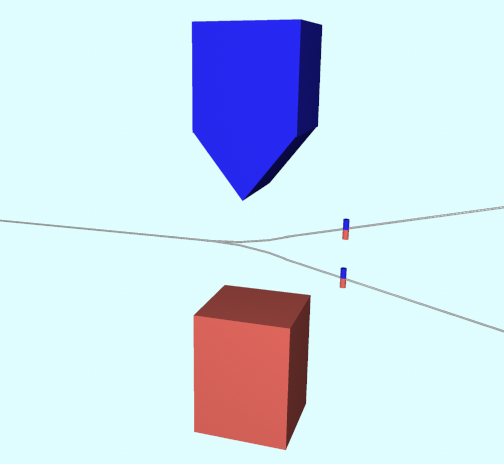上下方向　　左右方向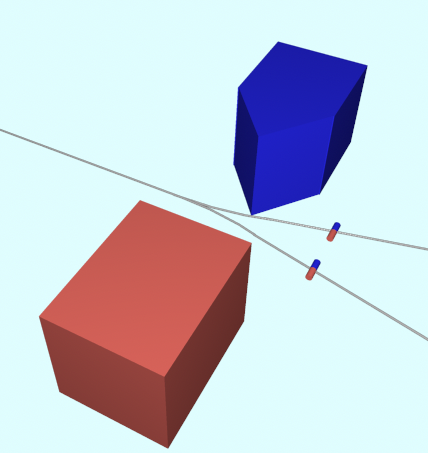

どの方向に磁場を掛けても、
その磁場の方向の正負の向きの二つに分かれる。

これからわかること

始状態の銀原子は

「上向き・下向き」の二つの状態の和でもあるし、

「左向き・右向き」の二つの状態の和でもある！？

＜疑問＞

(A)「上向き」の銀原子に、左右方向の磁場掛けたらどうなるの？

(B)「上向き」の銀原子に、もう一回上下方向の磁場掛けたらどうなるの？（左右→左右は？）

(A)の答えは▶に、(B)の答えは▼にある。

上下方向を２回続けた結果

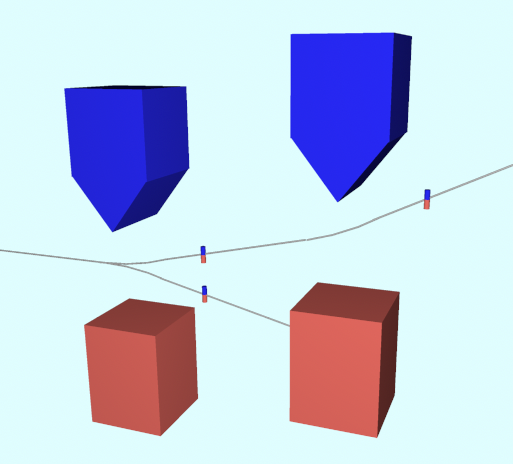左右2回なら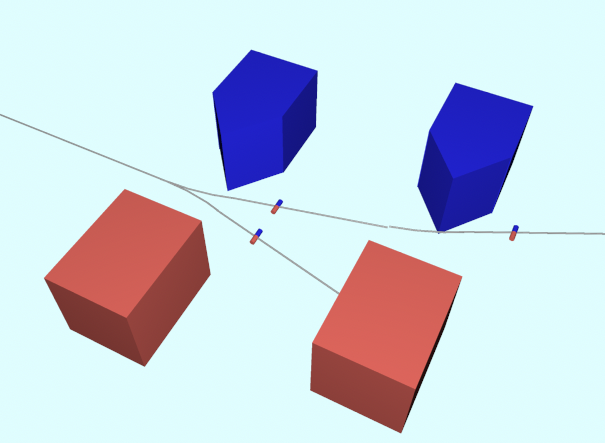

↑こうなる。

すでに「正の向き」だけを選別した結果なので、再実験しても「正の向き」しかなく「負の向き」は入ってない。

上下方向→左右方向と続けた結果

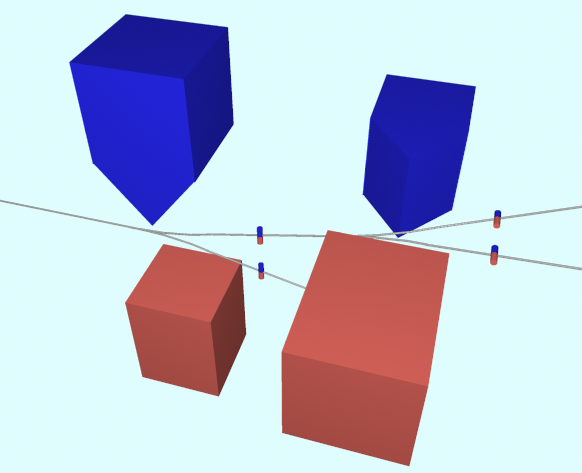
↑こうなる。

「上向き」の銀原子の中には、「左向き・右向き」の二つの状態が（重ね合わされて）入っている。

じゃあ、この結果に、$z$方向の磁場掛けたらどうなるの？

こうなる。→

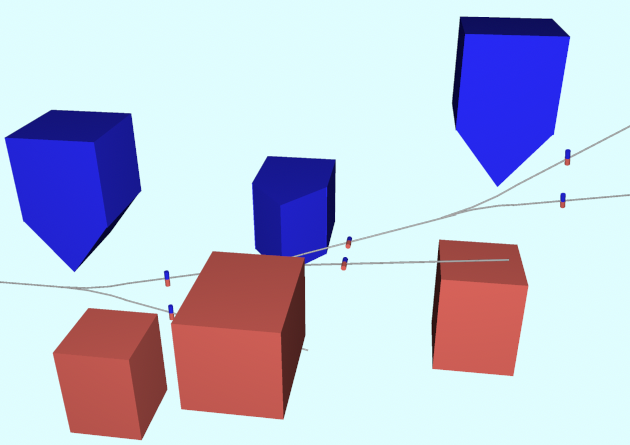
「右向き」の銀原子の中には、「上向き・下向き」の二つの状態が（重ね合わされて）入っている。

以上からわかること

「右向き」の銀原子の中には、「上向き・下向き」の二つの状態が（重ね合わされて）入っているし、

「上向き」の銀原子の中には、「左向き・右向き」の二つの状態が（重ね合わされて）入っている。

いったん「ある軸で正の向き」になればその後は「正」のみになるが、別の角度の実験装置を通すと、またその軸の「正または負」の向きに。

　銀原子は「磁石」のようなぐるぐる回せる物体であるというよりは、「（古典力学では回転の角運動量に対応する）不連続な量（スピンと呼ぶ）」を持っていると考えたほうがよい。

　この性質を、銀原子はスピン${1\over2}$を持つと言う銀原子の角運動量は$\pm{1\over2}\hbar$。

量子力学的に「状態」を記述する

　ここで状況を整理し、量子力学では「状態」をどのように考えるかを述べよう。

　量子力学的状態は、「重ね合わせ」になれる

たとえば、上向きの状態を$\mtx{c}{1\\0}$、下向きの状態を$\mtx{c}{0\\1}$と表すならば、左右方向を向いた状態は、$\mtx{c}{{1\over\sqrt{2}}\\\pm{1\over\sqrt{2}}}$のようになるだろう。

${1\over\sqrt{2}}$にする理由は、「長さ」を1にするため（詳しい説明は後でします）。

量子力学的状態は「足し算」ができる

　=　　+　？？

横向き状態は、上向き状態と下向き状態の「和」になっている。

　古典力学から考えると変だが、実験はそれを示している。


このあたりが最初に言った量子力学の「非常識」（のはじまり）なのです。

物理屋が使う「状態」を表す記号

「状態」は足し算できるそうだから、そのための記号を作ろう。
上向きの状態を$\ket{\uparrow}$、下向きの状態を$\ket{\downarrow}$、

右向きの状態を$\ket{\rightarrow}$、左向きの状態を$\ket{\leftarrow}$、

のように表現する。

実は$\ket{\rightarrow}={1\over\sqrt{2}}\left(\ket{\uparrow}+\ket{\downarrow}\right)$になっている。
一般的な状態は、
$\alpha\ket{\uparrow}+\beta\ket{\downarrow}$
のように「適当に係数を掛けて足したもの」で表現されている。
$\ket{\leftarrow}$と$\ket{\rightarrow}$では、係数$\alpha$と$\beta$の絶対値が等しい。

世界の状態が「状態の足し算で表現できる」というのは、逆に「そんな簡単でいいの？」という気分になってくるが、世界は意外と単純なこともある。

$\ket{\rightarrow}={1\over\sqrt{2}}\left(\ket{\uparrow}+\ket{\downarrow}\right)$なら、$\ket{\leftarrow}$は？


$\ket{\leftarrow}={1\over\sqrt{2}}\left(\ket{\uparrow}-\ket{\downarrow}\right)$です。引き算もありです。

上向きの状態は$\ket{\uparrow}=\mtx{c}{1\\0}$、下向きの状態は$\ket{\downarrow}=\mtx{c}{0\\1}$

左向きの状態は$\ket{\leftarrow}=\mtx{c}{{1\over\sqrt{2}}\\-{1\over\sqrt{2}}}$、右向きの状態は$\ket{\rightarrow}=\mtx{c}{{1\over\sqrt{2}}\\{1\over\sqrt{2}}}$

一般の状態は$\ket{?}=\mtx{c}{\alpha\\\beta}$で$\left|\alpha\right|^2+\left|\beta\right|^2=1$（長さが1になるように）

古典力学的磁石の状態


$(\theta,\phi)$で、いろんな$\theta,\phi$で状態が指定される。

量子力学的磁石の状態


$\alpha_\uparrow\ket{\uparrow}+\alpha_\downarrow\ket{\downarrow}$で、いろんな$\alpha_\uparrow,\alpha_\downarrow$で状態が指定される。

$\alpha_\leftarrow\ket{\leftarrow}+\alpha_\rightarrow\ket{\rightarrow}$で、いろんな$\alpha_\leftarrow,\alpha_\rightarrow$で状態が指定される。

$\alpha$は複素数の定数。

上の二つの表現は、どちらでも同じこと（$\ket{\leftarrow}=\alpha\ket{\uparrow}+\beta\ket{\downarrow}$のように表現されているから）。

古典的状態は実数変数二つで、量子力学的状態は複素変数二つで表現される？厳密にはちょっと違う（量子力学での変数は実数１個少ない）。

本質的な違いは変数の数だけではない（後述）。

ちょっと「高い視点から」見てみよう。

　$\ket{\uparrow}$と$\ket{\downarrow}$は赤の他人である。

↑を架空の空間の中で$\ket{\uparrow}$と$\ket{\downarrow}$は直交していると見る。

　$\ket{\leftarrow}$は、$\ket{\uparrow}$と$\ket{\downarrow}$の足し算である。

↑を架空の空間の中で$\ket{\uparrow}$と$\ket{\downarrow}$の混ざったベクトルが$\ket{\leftarrow}$だと見る。

　図で描くと 、のような感じ。

「現実空間」では、正向きと負向きの角度が180度だが、「架空の空間」では90度（直交）。「赤の他人」＝「直交」に注意。

この架空の空間を「状態空間」と呼ぶ。

　状態空間の中でになっているので、


$\ket{\rightarrow}$は$\ket{\uparrow}$の${1\over\sqrt{2}}$倍と$\ket{\downarrow}$の${1\over\sqrt{2}}$倍の和

となる。

状態の重ね合わせの意味

　銀原子1個だけを送ったとしよう。

こうなるのか？

違う（我々は「半欠け銀原子」を見たことがない）。

100回実験すると、が50回ぐらい、 が50回ぐらい起こる。

量子力学は決定論じゃない

　量子力学では、観測することによって状態が収縮する。

　この「観測する」は「測る」という動作を行うかどうかとは関係ない。SG実験のときのように「状態によって違う経路を取るように実験装置を設定して行き先を見る」ことも立派な「観測」である。

　この場合に「観測」という操作を行う前はどっち向きとも決まってない状態であったものが$\ket{\uparrow}$か$\ket{\downarrow}$かの決まった状態へと変わってしまうことが大事（常識に反するが、事実）なのである。

しかも、どちらに収縮するかを「予言」することはできない。
↑ここが古典力学からの大きな飛躍

量子力学的状態は古典力学的状態とは違う。


  • 状態は複数の状態の重ね合わせである。
  • 「観測」により、状態は重ね合わせのうち、どれかが選ばれる。
  • どれが選ばれるかは、確率的にしかわからない（前もって予言する方法はない）。

本当か？「確率的にしかわからない」のは人類がバカで量子力学という不完全な物理しか知らないからではないのか？

「前もって決まっているが我々は確率しか計算できない」と「そもそも決まってない」を区別する方法はあるか？

それが「ベルの不等式」である。

Einstein–Podolsky–Rosenのパラドックス

1935年、アインシュタイン／ポドルスキー／ローゼンは「量子力学による物理の記述は完全とみなせるのか？」というタイトルの論文を発表した。以下のような主張である。

量子力学の「観測するまで状態は決まってない」というのが本当なら、状態は複数の状態の重ね合わせであり、「観測」によりすぐに状態が決定する。

では「互いに離れた場所にある状態が関連しあっているならば、状態の収縮」は離れた場所にも瞬時に伝わるのか？

それは「局所実在性」に反しないか？？

アインシュタインたちは「局所実在性」は正しいと信じていたので、これを持って「量子力学は不完全だ」と言いたかったらしい。

つまり、

本当か？「確率的にしかわからない」のは人類がバカで量子力学という不完全な物理しか知らないからではないのか？

と。

　アインシュタインたちが考えた思考実験をスピンで考えてみる。

アインシュタインの考えた思考実験、および実際の実験よりも話を単純にしてます。

アニメーションで見てみよう。

アニメーションの解説が▼。まずは↑を実行して眺めて欲しい。

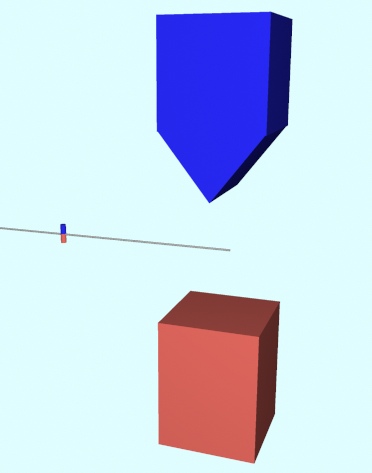
　真ん中の装置○から、それぞれ逆向きのスピンを持つ二つの粒子が発射され、両側に設置されたSG実験装置に向かう。

　二つの粒子は、両サイドで待ち構えているSG装置に届き、そこでSG装置の正の向きか負の向きか、どちらかの状態になる。

　SG装置を通り抜けた後は、それぞれのSG装置の方向の正負どちらか向きのスピンに変わって進んでいく。

　SG装置はマウスまたは指でつかんで回すことができるので、いろいろやってみよう。

　以上は古典的な考え方をした場合なので、「それぞれの場所で別々にスピンの向きが変わる」という現象が起きていることに注意。

　まずは古典的にはスピンがどのように変化していくかについて、確認できたろうか？

これはわりと「ふつ〜」に思える現象だ。

　古典的な場合「スピンの向きの変化」は各々のSG装置の場所で起こっている。

ことに注意しよう（あたりまえじゃん、と思うかな？）。

　では、量子的に考えよう。またアニメーションに行って、「古典的波動」と書いているところをクリックして「量子的」に変えよう。

アニメーションに関する解説が▼

　真ん中の装置○から、「まだ向きが確定してないスピン」が発射され、両側に設置されたSG装置に向かう。

　まず近い方のSG装置に「まだ向きが確定してないスピン」が到着する。

　近い方のSG装置で
状態が確定して、そのSG装置の中で見た上向き（$\ket{\bigtriangleup}$と書く）か下向き（$\ket{\,\bigtriangledown}$と書く）のどちらかになる。

　このとき同時に遠い方（右）のSG装置付近を飛ぶ粒子も状態が確定する。

　遠い方のSG装置に到着した粒子もまた、
そのSG装置の中で見た上向き（$\ket{\bigtriangleup}$と書く）か下向き（$\ket{\,\bigtriangledown}$と書く）のどちらかになる。

　こうして両方の粒子の状態が確定した。

　アニメーションで、「量子的」な場合について、左右のSG装置をいろんな角度にして実験を繰り返してみて欲しい。

  • SG装置を通過後の粒子のスピンはSG装置の方向の正負どちらかを向くこと
  • 片方のSG装置に届いたときにスピンの状態は（左右一斉に）変化することアニメーションではじわっと変化しているけど、当然この時間は一瞬です。
  • 実験結果の可能性は「両方△」「左は△、右は▽」「左は▽、右は△」「両方▽」の４通りがあるが、SG装置の角度によってどれが起こるかの確率が変化すること

を、じっくりと確認しよう。

この確率の相関が大事。

量子力学的状態とエンタングルメント

　ここでの量子力学的状態について考えてみる。今は「逆向きスピンが左右に飛ぶ」と考えた。左の粒子の状態には添字${}_L$を、右の粒子の状態には添字${}_R$をつけて表すことにしよう。

　発射したときの重ね合わせ状態は、左と右のスピンの向きが逆だという条件つき重ね合わせなので、

　単に左が$\alpha_1\ket{\,\uparrow\,}_L+\alpha_2\ket{\,\downarrow\,}_L$で右が$\beta_1\ket{\,\downarrow\,}_R+\beta_2\ket{\,\uparrow\,}_R$なのではなく、

${1\over\sqrt{2}}\left(\ket{\,\uparrow\,}_L\ket{\,\downarrow\,}_R\pm\ket{\,\downarrow\,}_L\ket{\,\uparrow\,}_R\right)$になっている。

ここで足し算にするか引き算にするかは、実は意味が違う（ここでは立ち入らない）。

　この${1\over\sqrt{2}}\left(\ket{\,\uparrow\,}_L\ket{\,\downarrow\,}_R\pm\ket{\,\downarrow\,}_L\ket{\,\uparrow\,}_R\right)$のような状態を「エンタングルした状態」と呼ぶ（「エンタングル」は「絡まる」とか「もつれる」とかいう意味）。

　これに左側で観測を行うと、

結果が$\ket{\,\uparrow\,}_L$だったら右側は$\ket{\,\downarrow\,}_R$になってしまう。

結果が$\ket{\,\downarrow\,}_L$だったら右側は$\ket{\,\uparrow\,}_R$になってしまう。

この「状態の収縮が伝播する」現象が、さっきのアニメーションで見た「●→-」とスピンの状態が変わる現象である。

　今ではこの「状態の連鎖」は「EPR（アインシュタイン・ポドルスキー・ローゼン）相関」と呼ばれている。

状態の収縮は超光速で起こるのか？

アインシュタインたちは、先のアニメーションで見せた「左側で観測を行うと遠く離れた右側の状態が確定する」という現象が起こるなんて信じられない、と考えました（人間の直感では、確かにそう思える）。
　しかも重要なことは「観測の結果どのように収縮するかは、確率でしかわからない」ということ。

最初の状態が決まっていれば、後の状態も全部決まる
というのが「決定論」ですが、たとえばシュテルン・ゲルラッハの実験でいえば「銀原子が二手に分かれる」ところは計算できるが、

１個の銀原子が出たとき、上に行くか下に行くか？

という問いに対しては、５０％の確率ですねという返事しかできない。

そんなのが物理と言えるか？というのがアインシュタインたちの意見。

果たして

結果は最初から決まっているーーー
のか
観測するまでは決まってなかったーーー
のか

それを区別する方法ってないですか？

その答えがベルの不等式

いよいよ、ベルの不等式

　ベルは、

もしも我々が知らないだけでスピンの状態は最初から決まってるのなら、この不等式が満たされなくてはならない

という不等式を求めた。

On the Einstein Podolsky Rosen Paradox(1964)

　実験によりこの式が成り立ってなければ最初から決まっているという考えを捨てなくてはいけなくなる。

　ベルがこの不等式を出した時点では「思考実験」だった。

もしも「最初から決まっている」のなら

↑の$\ket{\bigtriangleup}_L$は「左のSG装置から見て上向きスピン」を意味する（装置は回るので、実際は上とは限らない）。
$\ket{\bigtriangledown}_R$は右側の装置から見て下。
観測する前から、状態はこの図の「どこかの点」にあるはず。
だが、バカだから知らない？

先の図を四角で描いたもの

二つのSG装置が逆向きを向いていれば、

　発射される粒子は逆向きスピンを持っているから、結果は常に一致

二つのSG装置が同じ向きを向いていれば、

　発射される粒子は逆向きスピンを持っているから、結果は必ず逆

隠れた変数があると言う人の主張

　SG装置の配置により、いろんな図が描ける。量子力学信者は「どの状態になるかは最初は決まってない」と言うが、実はこの図のどこか一点にあるが、我々がそれを知らないだけなのでは？？？
この主張は、同じ状態に対して３種類の測定を行うことで否定できる。
　アニメーションで見せたように、逆向きスピンが左右に走る場合を考える。左側と右側でどのようなSG装置を待ち構えさせるかは実験する人が選ぶことができるので、三つの角度$\theta_a,\theta_b,\theta_c$のうち二つを選んで実験することにする。

アインシュタイン的（実在論的）考え

　実験する前から結果がSG装置を通った装置から見て上（△）か下（▽）になるのかが決まっているのだとすると、すべての状態を「３種類の角度について△か▽か」で８通りの状態に分類できる。

　量子力学の不思議な性質である、状態の収縮が起こるならば、「片方の装置の設定がもう片方の装置での測定に影響を与える」ことになるので、↑のような単純な分類はできない。

　量子論以前の考えでは、観測をやる前から結果がどうなるかは決まっている。つまり左の図のどこかが「現在の状態」である。
　実験することによって「あ、Aは△だ」とか「あ、Cは▽だ」とかがわかる。
　実験を繰り返すたびに「図の中の違う場所」が「現在の状態」なので▽△は確率的になる。。。。

↑と考えると何が言えるか？

　アニメで見た実験のように、二つの粒子が逆向きスピンを持って飛んでいく場合に左図の３つの角度での実験を、

　実験装置を、、、の三通りにして行ったときの結果を考える。

左でAが△、右でBが△ 左でA△、右でCが▽ 左でC△、右でBが△
$P(A+,B+)$ $P(A+,C-)$ $P(C+,B+)$

のそれぞれの場合の確率を考えてみる。

3種類の実験の詳細例は▼

左で角度Aの実験、右で角度Cの実験

左で角度Aの実験、右で角度Bの実験

左で角度Bの実験、右で角度Cの実験

≦ ＋
右辺の和は

である。つまり$P(A+,B+)\le P(A+,C-)+P(C+,B+)$である。

実験前から結果は決まっている（我々が知らないだけ）と考える限り。

量子力学での結果

　量子力学での計算では、このベルの不等式は破れる。

　簡単のため、三つの角度を

$\theta_A=0,\theta_B={\pi\over3},\theta_C={\pi\over6}$（それぞれ、0,30,60度）

としよう。

この「角度」は「状態の空間の角度」なので、実際の装置の角度はこの2倍

　詳しい計算は▼に書くが、$P(A+,B+)={3\over8},P(A+,C-)={1\over8},P(C+,B+)={1\over8}$なので、

　ベルの不等式は${3\over8}\le {1\over8}+{1\over8}$となって満たされない。

　量子力学の計算によれば、二つのSG装置の角度が$2\theta$だけずれると、「状態」の角度は$\theta$となり、一方が$\bigtriangleup$だったとき、もう片方も$\bigtriangleup$になる確率は$\sin^2\theta$（直交成分の長さの自乗）、もう片方が$\bigtriangledown$になる確率は$\cos^2\theta$（平行成分の長さの自乗）である。

　AのSG装置が先に「観測」するとして、Aにおける粒子が△を向く確率は${1\over2}$、このときBに来た粒子が△を向く確率は（直交成分の長さの自乗を計算して）$\cos^2{\pi\over3}={1\over4}$なので左$\bigtriangleup$右$\bigtriangleup$の確率は${1\over8}$。

　AとCの場合のAが△を観測する確率は${1\over2}$、このときCが▽になる確率は（CのAに平行な成分の長さの自乗を計算して）$\sin^2{\pi\over6}={3\over4}$なのでA$\bigtriangleup$C$\bigtriangledown$の確率は${3\over8}$。

　CとBの場合のCが△を観測する確率は${1\over2}$、このときBが△になる確率は（BのCに直交する成分の長さの自乗を計算して）$\sin^2{\pi\over6}={1\over4}$なのでC$\uparrow$B$\downarrow$の確率は${1\over8}$。

アスペたちの実験

　2022年のノーベル物理学賞を受賞したアスペらは、実際にこの実験に近いこと（偏光を使ったものもあるし、粒子のスピンを使ったものもある）を精密に行い、実際にベルの不等式が成り立ってないことを実験的に証明しました。

　Clauserたちの論文Experimental Test of Local Hidden-Variable Theories(1972)

　Aspect（アスペ）たちの論文Experimental Test of Bell's Inequalities Using Time-Varying Analyzers

我々はこれをどう解釈すべきなのか？

　ベルの不等式という、話だけ聞いていると当たり前に成り立ちそうな不等式は成り立たない。

　たとえ不完全に見えても、量子力学は我々の知る最善の理論である。

　「最善」ということの意味は実験で測れるものを完璧に再現するということ。そして古典論はその点で失格である。

　我々は「状態$\ket{\psi}$」そのものを「見る（観測する）」ことはできないし、その状態は「観測」によって（常識外れな）変化をしてしまう。

　最初に述べたように観測は、世界の一部を見せてくれるだけで、我々は観測できる事実からそれを説明する理論を作らなくてはいけない。

「ベルの不等式は満たされない」も、観測されている事実である。

よくある質問

量子力学的状態（あるいは波動関数）って、実際にあるものなんですか？

あなたの「実際に」という言葉の定義を教えてくれ。話はそれからだ。


重ね合わせ状態を観測できますか？

重ね合わされている状態のどちらにいるかを判別するような観測をしたら、結果はどちらかに収縮してしまうから、そういう観測をしたら重ね合わせ状態は見れない（ｚ軸スピンをはかったらｚ軸正と負の重ね合わせは壊れる）。

よくある質問続き

　状態の収縮が超光速なら、これを使って超光速通信はできませんか？

　今日の話を思い起こそう。あなたがどっちかの実験装置のそばにいて、自分の実験結果だけを見て、「あ、今あちら側の実験装置のSG装置の角度は何度だな」と判定できるだろうか？（あちらで偏光が通ったかどうかはこっちにはわからないことに注意）

　判定できるのは「こちらとあちらの実験結果全部を突き合わせをした後」だ。つまり「あちらの実験結果」を何か（電話？）で知らせてもらった後でないと、あちらの実験装置の角度はわからない。これでは超光速通信にならない。

おわりに

今日は、ノーベル賞を話題に、量子力学がどのように「常識やぶり」かという話をしました。

アインシュタインらが「常識からして量子力学は間違い」と主張したら、実は「常識のほうが間違ってた」ということがわかりました。こういうとが科学の世界では普通に起こるものです。

↓が「新しい常識」

量子の世界では状態は重ね合わせが計算できる「ベクトル」であり、観測により「状態」は不連続変化して収縮する。

　日常スケールで作られた＜常識＞はスケールが違えば成り立たない。

世界は不思議に満ちている。