光の質量に関するFAQ
相対論の話をしていると「光の質量」に関係したことで、あまりにも多く同
じ質問が(そのたびに説明しているにもかかわらず何回も何
回も)出るので、まと
めて書いておくことにした。
FAQその1:
光って質量
がないのに運動量があるの?
or
光って運動量があるのに質量がないの?
|
運動量というとmvすなわち(質量)×(速度)と覚えてしまうとこういう疑問が出るのは当然だが、運動量というものをもっと広く定義してあげないとだ
めなのである。
説明その1
ニュートン力学では運動量p=mvで、エネルギーE=mv2/2だった。だから運動量とエネルギーの関係は
2mE=
p2
となる。この式をみれば、m=0ならp=0になってしまいそうだ。
ところが相対論ではこの式は形をかえて、
p2 c2 + m2 c4 =E2
という式になる。この式は、E=mc2+εとして、εがmc2より十分小さければ、ε2を
無視するという近似では
2mε= p2
となって、非相対論的な式と同じになる(相対論的エネルギーは非相対論的エネルギーに比べmc2だけ言わば「下駄がはかされてい
る」)。
p2 c2 + m2 c4 =E2の
方にm=0を代入すると、p2 c2 = E2 となるが、この場合はp=0にはならない。p=E/cが解(pは運動量の絶対値を表しているとして、正だとしよ
う)である。
ところでこのp2 c2 + m2 c4 =E2で
特にp=0の場合の式が有名なE=mc2なのだが、元の式であるp2 c2 + m2 c4 =E2の方を見ずにE=mc2の方だけを見て「光もエネルギーがあるから質
量がある」と思っている人もいるようである。正しい式(p2 c2 + m2 c4 =E2)で考えれば、E≠0でも、m=0になっても問題ないことがわかる。
つまりエッセンスは「相
対論的な話をするのなら相対論的なエネルギー・運動量・質量の関係p2 c2 + m2 c4 =E2を使って話をしろ」と
いうこと。
説明その2
ニュートンは運動量と力の関係を
と書いている(ニュートン本人がこんなふうにライプニッツの記号を使って書いたわけではない)。これは別の書き方をすれば
F
dt = dp
であり、
ある「もの」に力が働けば、その「もの」の運動量が力に時間をかけた分だけ増えるということ。
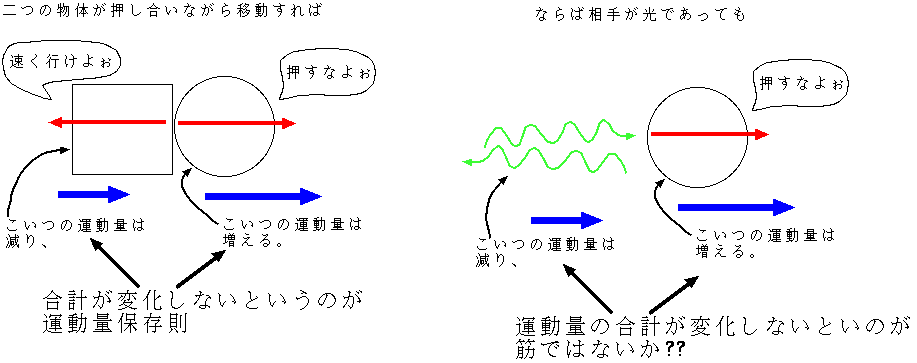
また、作用反作用の法則(二つの物体の間に働く力は向きが逆で大きさが同じ)とこの運動方程式を組み合わせると、「二つの物体の間に力が働
いていて、そ
れ以外には力が働いていなかったならば二つの物体の運動量の和は変化しない」という、所謂運動量保存則を導くことができる(左の図参照)。これはつまり、
ある「もの」に力が働いて運動量が増えたとすると、その力を働かせた「もの」の運動量は、ちょうどその分だけ減る。結果として二つの「もの」の運動量の
和は保存する。
ということ。高校物理の範囲ぐらいだと、ここで書いた「もの」というのは質量を持った物体に限っている。しかし、運動量保存則という便利な法則を使うため
には「力を働かせる」という作用があるものにはみんな運動量があるほうがいい。
光だって力を作用させることができる。たとえばコンプトン効果というのは光が電子を押すという現象である。だから、光にも運動量がある。
「光に力なんてない」と日常的感覚で思う人がいるかもしれないが、実際にはちゃんとある。その辺の電灯の光も、あなたや床や机や、光があたる物体を押し
ているのである。ただし、30Wの電球が出せる力は、その光を全部別の物体が受け止めたとしても、10-7ニュートンである。こん
なに小さいので普段認識せず「光に力なんてない」と思いこんでしまっているのである。思いこみは禁物だ。
そんな力があるなんて信じられない、という人のために、光が力を出せることを納得できる方法をもう一つ。光というのは電磁波である。電磁波とは、電
場と磁場が組になって波として進行するものである。電場は電荷にクーロン力を及ぼし、磁場は電流(あるいは、動く電荷)にローレンツ力を及ぼす。これを疑
う人はいない
だろう。光の正体である電磁場が力を出せるのだから、光も力を出せるに決まっている。
つまりエッセンスは「力を出せるものには運動量がある!」ということなのだ。
なお、実際に光の運動量を式で求める時には、クーロン力やローレンツ力が電荷にかかることによって、電荷の運動量がどれだけ増えるかを計算し、その時に
それに応じて減る量(電場と磁場で書かれる)を求める。
FAQその2
光は質量がないのに、なんで重力場
中で曲がるの??
|
これもちゅ〜〜とはんぱに一般相対論の話を聞いた人がよく考え込んでしまう疑問。重力を「質量×重力加速度」と機械的に覚え込んでしまうと、こういう疑
問がわくわけだけど、当然ながら、物事は相対論的に考えなくてはいけないのである。特に、一般相対論的に考えなくてはいけない。
というわけで、一般相対論において重力場中で物が落ちるというのはどういうことなのか、を考えてみよう。
注意事項として、一般相対論において、重力と他の力(電磁力とか分子間力とか)とは全く違う種類の力と考えられている。極端な言い方をすれば、
一般相対論の文脈において、重力は「力」ではない
のである。では何かというと、
一般相対論の文脈において、重力は時空の曲がりの影響である
と言える。
時空の曲がりというのも注意深く考えなくてはいけない。まず時空のうち時間の方への影響を述べておくと、
高
いところの方が時間がたつのは速い。
ということがある。この表現も誤解されやすいのでもう少しちゃんと書いておこう。そもそも「時間がたつのが速い」と言われても「速い遅いは誰が判断するん
だよっ」という問題があるわけである。とりあえず、誰かが決めてやらなくてはいけない。ブラックホールなど、一般相対論的に考える時は、「無限遠で静止し
ている人の時計と比較する」という形を取ることが多い。つまり、いろんな高さにある時計から、無限遠にいる人が「時報」を受け取るわけだが、その時報と時
報の間隔を無限遠で調べると、自分が持っている時計の時報と時報の間隔よりも長くなっている。
無限遠というのはつまり「一番高いところ」なので、この人から見ると、他の時計はみな遅れているように観測されるのである。無限遠から見ると、低いとこ
ろでは時間自体が遅くなっているので、その場所の光も(無限遠から見ると)スピードが遅くなることになる。
こう書くと「光の速さは一定ではなかったのか???」と文句を言う人がいるので先回りして弁明しておくと、特殊相対論の光速度不変の原理は、一般相対論
においては
光
が存在している場所の時間と空間の尺度で測れば、光の速度は一定
というふうに修正される。無限遠の時間の尺度と光が存在している場所の時間の尺度は違うので、無限遠にいる人からみたら光の速度が遅くなっても、しょうが
ない・・・・というか、そうなって当然なのである。
時空が曲がるとなぜ光が落ちるのかというと、幾何光学におけるフェルマーの原理(光は到着時間が最短になる光路を選択する)にしたがって光が進行するか
らである。
ある場所からある場所に光を届かせたいとする。どういう道を通れば最短時間で到着できるだろう?
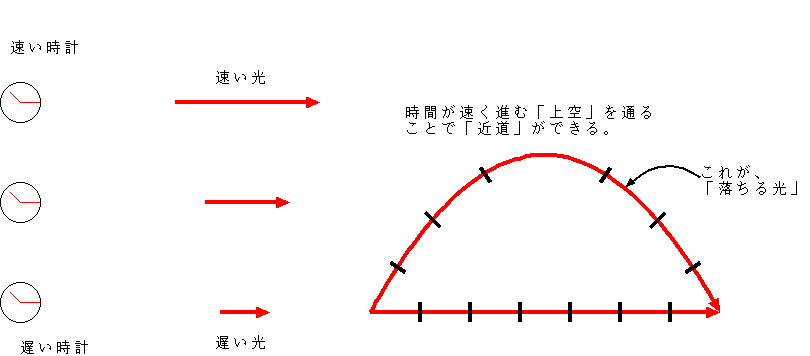
途中で水だのガラスだの、屈折率が違う媒質を通らない限り、「直線!」という答えになりそうだが、上で書いたように、光の速度が高さによって違うと、
「ちょっと高いところまで登って、光速の速い場所を通ることで時間が節約する」という戦略をとった方が、単にまっすぐ進むよりも速く到着できることにな
る。これが「光が曲がる」理由である。
なお、フェルマーの原理が成立する理由は実は「光が波だから」という点に集約される。つまり、
光が重力場中で曲がる理由に質量のあるなしは関係ない。
波であること、
波の速度が高さによって違うことが
大事である。時空の曲がりは時間だけでなく空間も曲げ、空間の曲がりも光の曲がりに寄与するが、フェルマーの原理で光路が決まるという点では同様で
ある。
質量のある物質が重力場中で進路を曲げる理由に関しても、物質を
(量子力学的に)物質波と考えれば同じ理屈で説明できることになる。ちなみに物質波に対してフェルマーの定理を適用するということは、本質的には力学にお
いて最小作用の原理を適用するのと同じことなので、別に量子力学を使わなくても、最小作用の原理を使えば物体の運動は計算できる。このあたりはややこしい
ので省略する。
FAQその3:
という誤解もたいへん多い。しかし、アインシュタイン方程式
Rμν - gμνR/2
=κTμν
を見てみるとわかるように、重力を作るのは(空間を曲げるのは)質量ではなくエネルギー運動量テンソルTμνなのである。
FAQその1に書いたように、光は質量はなくてもエネルギーや運動量はあるのだから、ちゃんと空間を曲げる(重力を作る)。