勝手に科学解説
2002年5月31日初版発行 早川書房 ISBN4-15-208418-9
この項は書評・感想というより、『かってに科学解説』というつもりで書く。そういうわけだから読んでない人は読まないように。以下の文中、緑のイタリックで示したのは「海を見る人」からの引用である。
本文の描写を見ていくとわかる通り、＜歪んだ円筒世界＞は回転による遠心力（擬似重力）が働いて外側が下になっている。これに対し、楕円体世界では自身の万有引力によって、楕円体（ではないがだいたいそういう形）の中心が下になる。カオスの谷はちょうど遠心力と万有引力がつりあって無重力状態になるところであるらしい。
検算はとにかく答えだけでいいからさっさと教えろという人は、ここまでジャンプ。
そこでこれを検算するとともに、これらの世界がどんな形をしているのかをグラフで表してみよう。実際の状況にそった計算をするのは難しいので、ここでは近似として、楕円体世界が作る重力は中心に質量が集中していると考えて計算したものと等しいと考えよう。具体的には、楕円体世界の質量をM、万有引力定数をG、中心から、外側へ向かう距離（左の図で言うと横軸）をｒ、北へ向かう距離（左の図で言うと縦軸）をｚとすると、万有引力による重力ポテンシャルが
-GM／(r^2+z^2)^(1/2)
で表せるということである。「え、いつでもこうじゃないの？」と思ってはいけない。楕円体世界は球対称ではなく南北に押しつぶしたような形になっているから、これとは多少ずれるはずなのである。このポテンシャルはｒやｚが小さいほど小さい。つまりｒやｚが小さいほうへとひっぱりこむ力を表している。
これに遠心力によるポテンシャル
-r^2ω^2/2
を加える。
この力はｒが大きいほど小さいので、外へ放り出す力になっている。
あともう一つ、円筒世界からも重力が働くはずである（もし円筒が完全な円筒なら重力は打ち消されるが、括れの部分で対称性が破れているから、そうはいかないはず）。これも面倒なので無視しよう。
楕円体世界の半径をaとしよう。r=a、z=0の場所で、重力は０になる。これは、
GM/a^2-aω^2＝０
が成立する、ということだ。そこでGM=a^3ω^2として代入しつつ、ポテンシャルを整理すると、
-(a^3／(r^2+z^2)^(1/2)+r^2/2)ω^2
となる。これが一定になるという条件をおく。ということはrとｚの間になんらかの関係がつくということだから、zをｒの関数だと考えろ、ということ。これで(r,z)面の上に線が引ける。
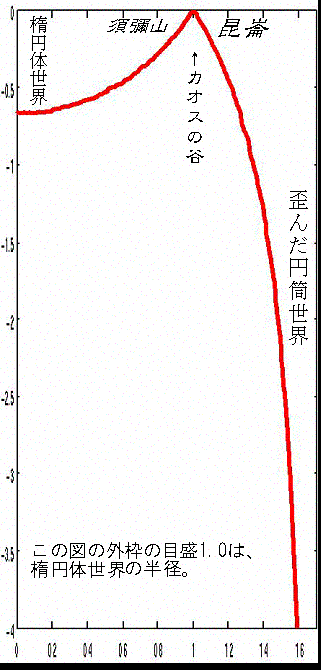r=aでz=0であるという条件をつけると、上の定数が3a^2ω^2/2だということなので、これをとくと、
z=±sqrt(4a^6-9a^4r^2+6a^2r^4-r^6)／(r^2-3a^2)
という解が出た。これをグラフにしたのが左の図である。グラフの中ではa=1にしてある。
というわけで、グラフの赤線が等ポテンシャル面だということになる。この図の原点（左上の0）が楕円体世界の中心である。原点でのｚはaの2/3倍である。また、このグラフをどんどん下に伸ばしていくと、ｒ=sqrt(3)×aになるとグラフはタテにまっすぐになり、それ以上ｒは増えない。このような状況は、作品中の
＜楕円体世界＞と呼ばれてはいるが、厳密には楕円体ではない。縁が微分不可能な稜線になっているのだから、むしろ凸レンズに近い。凸レンズはその縁を砂時計の内面に接している。凸レンズの直径はその厚さの一・五倍。砂時計の括れの内側の直径ももちろんそれに等しい。砂時計の内面は凸レンズから離れるにつれ、円筒に漸近していく。その円筒の直径は括れ部分の一・七倍になる。
という描写にぴったり一致する。いや、一致しすぎている（後述）。この直後には
凸レンズの外面と砂時計の内面は一組のポテンシャル面を形成している。視覚的な高低差にもかかわらず、ポテンシャル的には二つの世界のどの場所もほぼ同じ高さなのだ。
という文章がある。このポテンシャル面というのがまさに左の図の赤線なのである（実際の円筒世界を考えるには、この図が左の縦線（実際にはここには＜光柱＞がある。図に書き込んでおくの忘れた）を中心にぐるぐるまわした時にできる形を思い起こせばよい。
「視覚的な高低差にもかかわらず、ポテンシャル的には二つの世界のどの場所もほぼ同じ高さなのだ」という意味がわかりにくいかもしれないので少し解説を加えておく。重力はこの赤い線と垂直に働く。ただし、＜歪んだ円筒世界＞の上では図の右、つまり外側に。＜楕円体世界＞の上では図の上、つまり中心側に。つまりこの赤い線（要はこの世界の地表なわけだが）の上に立つと、つねにそれに垂直な方向を「上下」と認識するわけである。つまりこの赤い線にそって動くかぎり、重力の方向には動かないので、「坂を登っている（降っている）」という自覚がない（というか、登っていないのである）。主人公である族長が崑崙に登っていると思わぬうちに登ってしまっている、という描写がある。この図の下の方から上の方に移動したと思えばよい。その時、「ｚが小さくなる」という意味では「登っている」のだが、あくまで重力と垂直に動いているという意味では、全く登っていないので、こういうことになるわけだ。
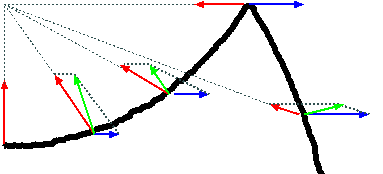さて、「計算したらこうなりました」だけじゃあまりに愛想がないので、なんで上のグラフのような結果が出てくるのか、図的に解説をしておこう。まず万有引力であるが、これは楕円体世界の中心に向う力で、遠くにいくほど弱くなる。左の図に描かれた赤の矢印のような感じである。一方遠心力は青で描いた矢印のように、常に外側を向き、外にいけばいくほど強くなる。このような二つの力が足された結果を、図では緑の矢印で描いた。この赤青緑の力をみると、なぜ上のような結果が出たかがわかってくる。楕円体世界の上（図では左の方）では赤い力の方が強いから、だいたいその中心へ向かう力が働くことがわかる。しかし青い力も（図の左端の＜光柱＞があるあたりを除けば）０というわけではないので、楕円体世界の上でも遠心力（図の青い力）は働き、その分、楕円体世界の上の人が感じる『下』（緑矢印の向く方向）は、外にそらされることになる。つまりほんとの中心ではなく、少し須彌山側によったところを『下』と感じるわけだ。これは上のグラフの方でも確認できる。
円筒世界の上では青い力の方が圧倒的だから、『下』はつまり外である。ところが楕円体世界に近いところでは赤い力も働くので、その付近での『下』は少し赤道よりにずれることになる。それがグラフの線の傾きに表れているのである。カオスの谷ではちょうどこの力はうまくつりあって０になるようになっている。地面（黒の線）と合成された重力（緑の矢印）が常に直角であることに注意して欲しい。
ちなみに、重力の大きさがどんな感じになっているか、計算してみたのがこのグラフ。このグラフの横軸はｒ。＜楕円体世界＞および＜歪んだ円筒世界＞の表面における重力加速度のグラフである。横軸はｒで、a=1として表してある。縦軸の方は重力加速度だが、r=sqrt(3)aのところ（つまり＜歪んだ円筒世界＞の表面部分）で重力加速度が9.8（つまり我々の地球での値）になるように調節した。
グラフを見ると、北極ではちょっと強い重力が働くことになるのがわかる。主人公たちは物語の終わりにおいてやっとカオスの谷を越えたところであるが、この後はどんどん重力が大きくなっていくわけだ。
ところで上で「一致し過ぎている」と書いたが、その理由はここでは二つの近似を行ったからである。思い出しておくと、
・楕円体世界は球じゃないのに、球対称な重力場を仮定した。
・円筒世界にも質量はあるのに、それを無視した。
という二つだった（無意識にもうちょっとやっているかも）。それなのにこううまく一致したのはなぜだろう。考えられるのは、
(1)小林泰三も同じ近似をした。
(2)この近似は非常にいい近似であり、「差が出るはず」と思っている私が間違っている。
(3)実は近似でなく、そういう設定である。つまり円筒世界はほんとに質量が無視できるぐらい小さい。また楕円体世界は外から見ると球ではないが、実はほとんどの質量は球対称に分布している。
(4)その他、思いもつかない理由。
などが考えられる。さてどれだろう。たぶん(2)か(3)じゃないかなぁ？
最後の方で「おや？」と思わせるところがある。
日本列島？
もしかしてこれって地球なんかい。どこにあるんだ自由の女神は（ってそれは違うでしょ）。そこでここでもちょっと検算をしてみよう。上の計算で楕円体世界の質量がどれくらいであるかは計算できる。まず本文中に、崑崙の高さが５０００キロぐらいとある。つまり、sqrt(3)a-aが5000キロぐらいということになる。ということはaはだいたい683０キロぐらいと思っていいだろう。上で、GM=a^3ω^2ということがわかっている。ωはまだわからないが、円筒世界上での重力が１ｇだということにすれば、sqrt(3)aω^2が9.8ぐらいになるということから、ω＝0.00090。dだいたい7000秒で一周する各速度である。これから、a^3ω^2を計算してGで割ると、3.9×10^24キログラムとなる。
地球の質量はだいたい6×10^24キログラム。少し小さいが、もともと球である地球を凸レンズ型に削った（削ったんかどうかしらんけど）と思えばそう悪い数字でもない。ちなみに、地球の半径は6400キロなので、aが6830キロというのと、そう悪い数字ではない。
＜かたもの細工＞と＜やわもの細工＞は地球つぶして＜楕円体世界＞にして、周りを＜歪んだ円筒世界＞で包んでこの世界を作ったわけね。なんでそんなことをしたのか、脱出プロジェクトって何なのか。そこは私にもよくわからないのだが。
この世界は、ブラックホールの表面近くに住む人の話である。そこでブラックホールの表面ではどのような運動をするのか、を考えよう。ここからしばらく、ブラックホールの近くでは空間が曲がっているというのはいったいどういうことか、ということを解説する。例によって、ややこしい計算はいいから結果を先に見たい人は、ここまでジャンプ。
今回、調子にのって「ブラックホールの近くで空間が曲がっているってのはいったいどーゆーことやねん」という話をくどくどと数式も使って書いたので「そんなん、かなわんわぁ」という人は、迷わず、ここまでジャンプしてほしい。実際「海をみる人」の解説をするだけなら、こんなにくどくどと書く必要はなかったなぁ、と書いた本人が思っているぐらいだから。
「前々から、空間が曲がっているってどういうことか、なんか実感できんかってん」という人は読んでみてください。これで絶対わかる、、、、などとは保証いたしませんが。
相対論の本などを見ると、ブラックホールを表す計量として、
ds^2 = -(1-a/r) dt^2 + dr^2/(1-a/r) + r^2 (dθ^2 + sin^2θ dφ^2)
という式が書いてある。これは、曲った空間の中で、長さがどのように定義されているかを表している。このaを０にした式
ds^2 = -dt^2 + dr^2+ r^2 (dθ^2 + sin^2θ dφ^2)
は平坦な空間の式である。この式を見ると、
「θやφやｔは変化せずに、ｒからｒ＋ｄｒまで移動すると、その距離はdrである」
とか、
「rやφやｔは変化せずに、θからθ＋ｄθまで移動すると、その距離はrdθである」
ということがわかる。どういう計算をするかというと、上の場合なら、dθ=dφ=dt=0(dθというのはθの変化量を意味する）としてからdsを計算する。下の場合ならdr=dφ=dt=0とするだけで後は同じ。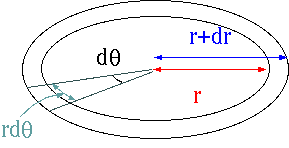
この結果自体は極座標をとっていれば普通のことである。たとえばｔ、ｒを変化させず、θはずっとπ／２に固定しておいて、φだけを０から２πまで変化させたとする。すると上の式から計算すると距離は２πｒという答えになる。これはつまり、半径ｒの円周をぐるっと回ると２πｒの距離だということを示している。特に、円周2πｒの円と円周2π(r+dr)の円を二つ持ってきて中心があうように重ねると、二つの円の隙間はdrになる。当たり前である。しかしそれが当たり前でなくなるのが空間が曲がっている場合なので、この当たり前の結果を覚えておいてほしい。
なお、rもθもφも変化せずにtだけ変化する、というのはその場に静止していることを意味する。このときはdt=idsとなる。この場合のisというのはその物体にとっての時間となる。止まっている場合なら、『座標の時間』tと『物体の固有時間』sは等しいが、もし物体が動いていると(つまりdrとかdθとかが0でなければ)、その分idsは小さくなる。つまり、物体が動いていると固有時間は遅くなる。ウラシマ効果というやつである。
ところがブラックホールの近くではそうなっていない。違いはdr^2の前の1/(1-a/r)とdt^2の前の(1-a/r)である。
dtの方の係数は、場所によって時間の経過が違うことを意味している。r=∞においてはids=dtなので、曲がってない空間の場合と同じとなる。つまりブラックホールから遠いところでは、時間とidsは一致する。ところがrが小さくなると(1-a/r)が小さくなっていく。それはつまり、r=∞にいる人に比べ、ブラックホールの近くにいる人の時間が1/sqrt(1-a/r)倍だけ遅く進むことを意味するのである。
ｄｒの方の係数は何を意味するかというと、この座標系（シュワルツシュルト座標系）の場合、
「θやφやｔは変化せずに、ｒからｒ＋ｄｒまで移動すると、その距離はdr/sqrt(1-a/r)である」
ということになってしまうのである。つまり、ｒはシュワルツシュルト座標系の中では距離という意味を持っていないのである。実際の距離は1/sqrt(1-a/r)がかけ算されている文だけでかいのである。ところがシュワルツシュルト座標系でも、
「rやφやｔは変化せずに、θからθ＋ｄθまで移動すると、その距離はrdθである」
の方は同じである。つまり、半径方向だけ、長さが変なことになっているわけである。
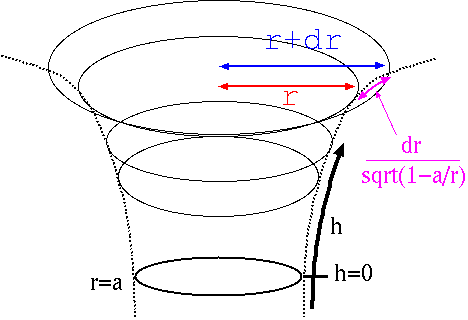
実際には３次元の空間の話なのであるが、例によってそれを絵に描くのは難しいので、赤道部分だけを考えていく。ブラックホールを中心とする円周2πｒの円を考える。その外側には円周2π（r+dr)の円がある。ところが、この二つの円の間の隙間は、ｄｒより大きい。具体的には、dr/sqrt(1-a/r)となる。こういう状況は平面では起こらないが、曲がった面の上でなら起こる。右の図を見てほしい。ブラックホールの解説書というとやたらにこの漏斗状の図が出てくるが、その意味することはこういうふうに、長さが変になっていますよ、ということなのである（念のため註：同じような図で、重力ポテンシャルを書いた図もある。だいたい同じ形なのだが、一応別物である）。
ところでr=aになると、本当の長さであるところのdr/sqrt(1-a/r)は無限大になってしまいそうだ。しかしこの時は実はｄｒの方も０になっている。つまり、この漏斗が垂直になってしまって、いくら下にさがってもｒが変化しなくなっている状態（図を参照のこと）なのである。
よく「ブラックホールの周りでは空間が曲がっている」と言葉で言うのだが、何がどう具体的に曲がってるんだか、理解するのは難しい。そこで少しでも具体的に「曲がっているなぁ」と思えそうな説明をしてみた。なお、上では２次元で考えて、円の重なりで考えたのであるが、実際のこの世は３次元なので円の重なりでなく球の重なりで表現すべきである。そして、球と球の隙間が単純な予想より長い、というイメージを想像してくれればいいのである（ちなみに、たいていの人間はそんなものを想像すると大脳がばらける）。
さて以上からわかるように、ブラックホールの表面を考える時、ｒはあまりよい座標ではない（ほんとの意味の長さとあまり関係がないから）。そこで、図に書いたｈのように、r=aを出発点にして、上向きに、ほんとうの長さにしたがって増えていくような目盛り（というか、座標）を選ぼう。つまり、ｒの代わりにｈを座標として使う。さらに、hはaよりも十分小さいということにして、近似してしまうとどうなるかを計算しておく。すると、時空の計量を表す式はこうなる。
ds^2 = -h^2/(4a^2)× dt^2 + dh^2+ （a+h^2/(4a))^2 (dθ^2 + sin^2θ dφ^2)
さて、ここまできたところで、時間に関係する部分を考える。物体が止まっている場合を考えると、この式は、ids=h/(2a)×dtまで簡単にできる。このidsは上にも書いたように、そこにいる物体（人でも可）にとっての時間である。そしてdtは何かというと、r=∞にいる人の時間である。まぁ今は、ブラックホールの表面近くだけの話をしているので、r=∞なんて遠くはどうでもよい。大事なことは、ｈと時間の経過idsが比例することである。つまり、ブラックホールの近くでの時間は、地平線（r=aまたはh=0）からの高さhに比例するのである。ただし、この式はｈが小さい（表面近い）ところでしか使えない式であることに注意しなくてはいけない。
というわけで、低いところほど時間が経過するのが遅く、逆に高いところほど時間の経過が速い、という場所が、ブラックホールの表面近くでは実現するわけである。
このｈという座標ではかって、主人公『わたし』のすむ村はカムロミの住む浜の村の１００倍の高さの場所にあることになる。カムロミは、１階と２階で２０分の１ぐらい時間の経過が違う、と言っている。浜の村はかなりh=0に近いはずなので、上の近似が使えるとしよう。そうすると、高さと時間のすすみ具合が比例する。ということは、逆に考えると、カムロミの村の地下２０階にあたる部分では、時間が停止する。つまりh=0は、カムロミの村の地下２０階（もちろんそんな家はないだろうけど）にあたるということがわかる。ということをそのまま外挿すると、『わたし』の住む村は地上２０００階あたりにあるということになるが、これは少し怪しい。hが小さいという近似からはずれる可能性があるからである。
「海を見る人」の中には、主人公が
ところで、ここから海までの距離を知ってますか？ ここから、海までだいたい二百五十キロメートルほどですが、実際には例の時空変換のおかげで、それよりもかなり短い距離を歩くだけで到達できます。逆に、ここは海抜五キロメートルぐらいですが、実際に浜に降りるには十キロメートルも下らなくてはなりません。
と述べるところがある。ここで単に「距離」と書かれている距離と、「実際に」という枕言葉つきで書かれている距離と、二種類の距離があるようである。おそらくこれは上のrとｈに対応するのであろうと考えられる。
たとえば「海抜五キロメートル」はｒ、つまり上の漏斗図で言うと半径方向の『距離』なのであろう。そして、「十キロメートル」はh、つまり上の漏斗図の漏斗に沿って降りていく距離（実際に歩く時の距離はこっちなのである）なのであろう。念のために注意しておくと、rとhはスケールが違うだけで、どちらも上下方向であるという点に違いはない。水平方向は漏斗図で言うならば円の円周方向である。
「時空変換のおかげで、それよりもかなり短い距離を歩くだけで到達できます」の意味は実はまだよくわからない(^^;)。ここでの距離は横向きの移動を含むので、rdθの方になるのではないかと思うのだが、としたらどないなるんかな？？？
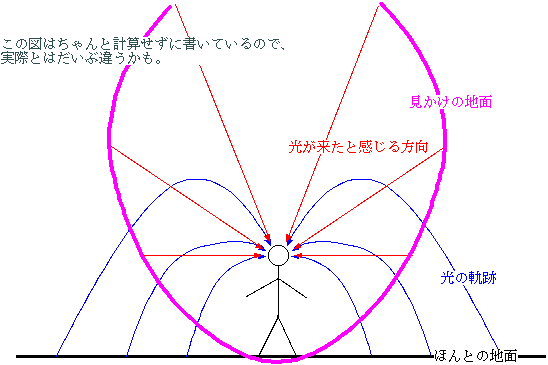この世界がブラックホールの表面付近だとすると、光はぐにゃぐにゃと曲がってしまう。重力のために、光も“落下”するのである。そのために、作中の描写のように、「地面は自分から離れるにつれてせり上がって、まるですり鉢の底にいるみたいで、村全部ですら見渡すこともできないし、空はすぼまってストローから覗くみたいにしか見えない」ということになる。なんでそうなるのかは図を見てもらえばわかると思う。地面から出た光は、いったん上の方に行った後、人間の目に向かって落ちてくる。そのため、人間は地面が上にあるように感じてしまうのである。そして空からの光は、自分の頭上のほんの狭い部分からだけやってくることになる。
そこで＜人の子＞たちは光でなく超光なるものでものを見ているらしい。この超光の性質については、以下のような説明がある。
高いエネルギーを持った遅い超光は光とほとんど同じ振る舞いをします。＜人の子＞が感じることができるのはこれとは逆にエネルギーをほとんど持たない速い超光だということです。
これは物理学者がタキオンと呼ぶ超光速粒子と同じである。なぜ超光速粒子は高いエネルギーだと遅くて低いエネルギーだと速いのか。それは相対論で粒子の持つエネルギーと運動量にどんな関係がついているか、ということに関係する。普通の粒子がエネルギーE、運動量ｐを持っている時に、
E^2 - (pc)^2 = m^2c^4
という式が成立している。これはp=0（運動量が０つまり止まっているということ）である場合、E=mc^2というおなじみの式になる。で、Eやpはどう書けているかというと、
E=mc^2/sqrt(1-(v/c)^2) p=mv/sqrt(1-(v/c)^2)
という式になっている。速度はp/Eと表すことができる。
超光の場合、v>cになるので、この式をそのまま使おうとすると、Eが虚数になってしまう。エネルギーが虚数なのは困るので、超光の場合、質量もm=iMと（Mは実数）のように虚数だということにする。すると、
E=Mc^2/sqrt((v/c)^2-1) p=Mv/sqrt((v/c)^2-1)
となる。すると今度はおもしろいことに、v<cになるとエネルギーが虚数になって変なことになる。つまり超光は逆に、光速より遅くなることができない。また、vを∞にするとエネルギーは０になり、運動量はMになる。
そもそも、普通の粒子が光速をこえられないのはなぜかというと、v=cに近づくと、エネルギーが∞になってしまうからである。そして、超光に関する式を見ても、やっぱり「v=cに近づくと、エネルギーが∞になってしまう」のである。だから、普通の粒子を光速まで速度を上げるのに∞のエネルギーがいるのと同様に、超光の速度を光速まで下げるのにも∞のエネルギーがいるのである。逆に、速度vが速ければ速いほど、エネルギーは小さくなる。
質量が虚数なんて物理的におかしいんとちゃうんか、ということをよく聞くが、別におかしくない。ここのm、つまり相対論における質量というのは「静止している時のエネルギーをc^2で割ったもの」というのが定義である。だから、そもそも静止することがないタキオンに対してmを計算して虚数だなんだと言ってみても意味がないのである。タキオンの場合のMはいわば「無限速度運動量」とでも呼ぶべきもので、断じて「虚数になった静止質量」などと解釈してはいけないのである。
さて、普通の光は上の図のように曲がるが、超光はどのように曲がるのだろう。それを理解するために、まず普通の光が曲がってしまう理由を考えよう。光というのは「最短距離を通ろうとする」という性質がある。上の絵を見ても青い線（光が通る線）はちっとも「最短距離」に見えないかもしれない。しかし、「なるべく短い時間で到達する」という意味では、確かにこれは最短距離なのである。
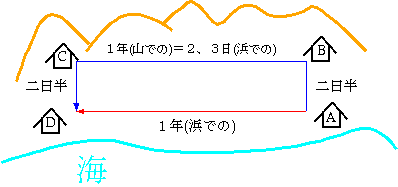なぜなら、ブラックホール付近では（作中での浜と山の差のように）高いところほど時間が速く進む。だから高いところを通過した方が結果として速く到着するのである。これを理解するには左の図を見てほしい。浜に村A,村Dがあり、山に村B,村Cがある。村Bは村Aのほぼ真上にあり、村Cは村Dのほぼ真上にあるとしよう。村Aから村Dまで、まっすぐに浜を歩いていくとしたら１年旅をしなくてはいけないとする。
しかしここで、A→B→C→Dと移動したらどうだろう。村Bから村Cも、だいたい１年かかるはずであるが、この１年は山の時間の１年であり、浜の時間でいえば２，３日に過ぎない。だから、実は青で書いた経路A→B→C→Dの方が短い時間でいけるのである。『最短時間で行こうとする』が、光が曲がる理由であると言っていいだろう。
とここまで書いて考えたが、実際にあの世界で浜の人間がＡからＤへ行くとしたら今説明したような経路を通った方が速いんだろうか？
だとすると、わざわざ浜の人間が山に行く理由はその辺にあったりするのかな？？？
では、超光の場合はどうか。特にエネルギーが０の超光の場合、移動に時間がかからない。つまり『最短時間で行こうとする』ということにはならない（時間は全部０なんだから）。時間でなく『距離を最短にしようとする』ということになる。では曲がらないのか、というとそうではない。実は時間方向に移動しないということは、超光のたどった軌跡は上に書いた漏斗状の絵の上に書かれた測地線（距離が最短になるような線）になるということである。漏斗状の形は当然平坦でないので、その上に線を書くと、やっぱり曲がる。それはやはり、いったん上に上がってから下がってくるという線の方が距離が短くなるだろう。やはり超光とはいえ、“落ちる”のである。ただしもちろん、光の場合より落ち方はずっと小さい。だから、超光を使えばわりと普通に（「普通に」って何が普通やねん、と言いたくなるが、まぁとにかく「普通に」）ものを見ることができるのである。そして、その超光の中でもわりとエネルギーの大きい（ってことは遅いって言うことなのだが）やつは曲がり方としては光に近くなる。よってうまく使う超光のエネルギーを調節してやれば、遠くの光を見ることができることになる。といってもその遠くからの超光はいったん上にあがってから落ちてくるのだから、上を見るように見なくてはいけない。そういうこというと光だって遠くが見えそうなものだが、光は曲がり方が強すぎて、遠くのものがほぼ一点にぎゅっと圧縮されてしまって見にくいのである。
ところで謎なのは、この「海を見る人」の舞台である世界では、光速それ自体が我々の世界とは変わっている。山の村で引かれるだんじりが速すぎて光だとぐにゃぐにゃになってなんだかわからない、という描写があるのである。そして、超光で見てもぺしゃんこになって見える、という記述もある。つまり、だんじり程度のものが亜光速（作中では準光速）で動いてしまうのである。
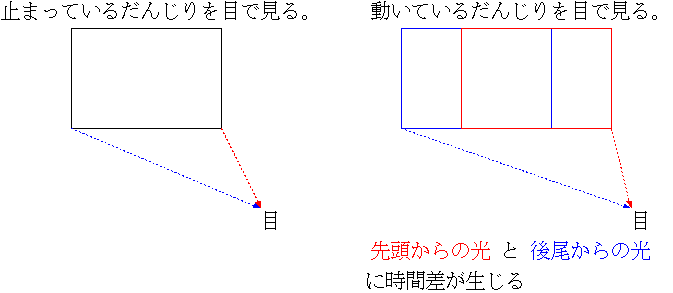超光はだいたい「現実にある通り」のものを見せると考えていいので、ぺしゃんこに見える理由は相対論の教科書そのままのローレンツ短縮の結果と見ていいだろう。では、なぜ光で見るとぺしゃんこになる以上におかしな形に見えるのかというと、図に書いたように、先頭から来る光（図に赤で示した）と後尾から来る光（図に青で示した）が、別の時刻に出た光だということから来る。止まっているならば、結局はそこにあるものがそのまま目に見えることになる（さっき述べた重力が原因での曲がりはちょっと置いておいて）。ところが、だんじりが図の場合は右に動いている。先頭から来る光の方が後尾から来る光よりも短い距離を飛んでいることに注意。このため、この場合だんじりは実際よりも長く見えることになる。ローレンツ短縮しているから縮んで見える、と思ってはいけないのである。
ところで今の話はだんじりの「目」がある側の側面から来た光だけを考えて、だんじりの前か後かによって時間差が生じる、と言ったわけだが、実際にはだんじりの「目」側（進行方向向かって右）か逆側（進行方向向かって左）かでも時間差が生じ、ますます見えるものは実際のものとは違って見えることになる。これ以上はややこしいので省略するが、要は光で見たらぐちゃぐちゃに見えるということだ（我ながら投げやりな説明だな）。
なお、超光でももし多少なりとも時間がかかるなら同じことが起きる。ただし、どうやら超光はほぼ時間がかからないでやってくるようである。
ところで、どうしてこの世界では光の速度が小さく設定されているんだろう？というのが次の疑問になるところだが…というところで
（もっともこの疑問の解決編は結局書かないかも(^^;)）