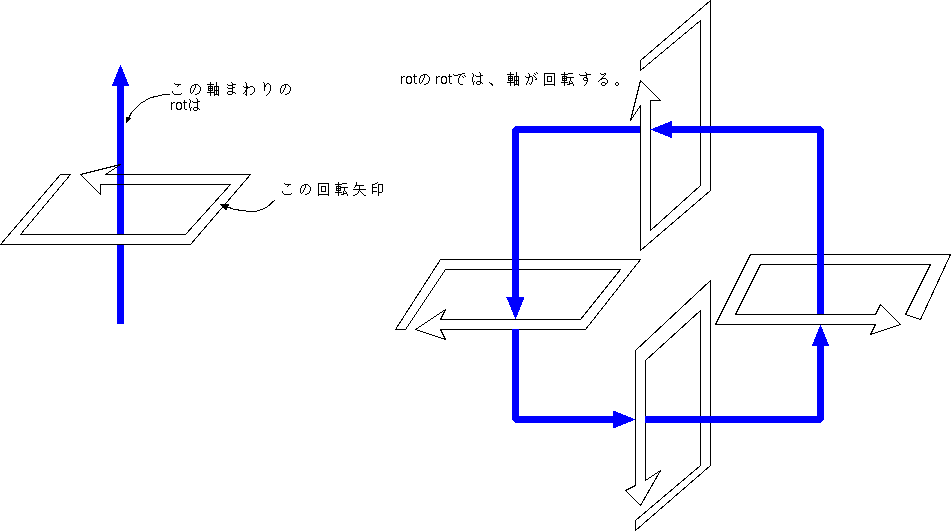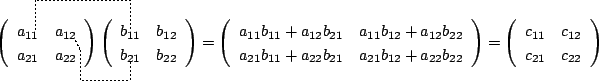
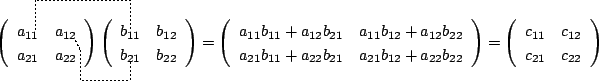
|
(2.23) |
| A = | |
|
|
|
|
(2.24) |
|
(2.25) |
|
(2.26) |
|
(2.27) |
|
(2.28) |
|
(2.29) |
|
(2.30) |
|
(2.31) |
|
(2.32) |
|
(2.33) |
|
(2.34) |
|
(2.35) |
|
(2.36) |
|
(2.37) |
|
(2.38) |
|
(2.39) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.40) |
|
(2.41) |
|
(2.42) |
|
(3.1) |
|
(3.2) |
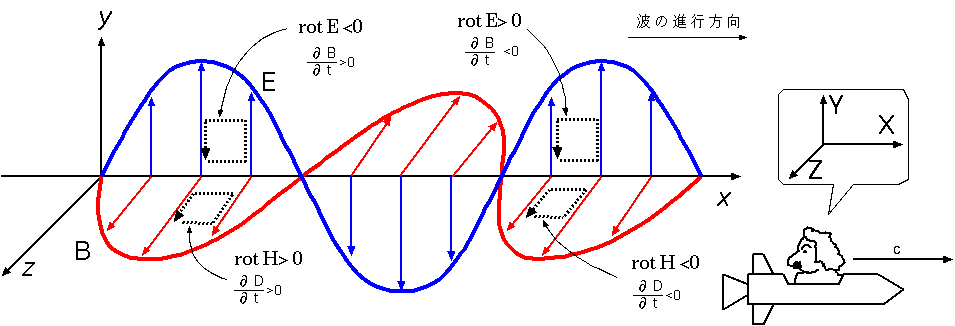

 ˇˇ¸ą¤Îż¶Ć°¤Îľěąç¤ňąÍ¤¨¤ëˇŁĄÔĄó¤ČÄĄ¤é¤ě¤ż¸ą¤Ë¤ĎÄĄÎϤ¬ĆŻ¤¤¤Ć¤¤¤ëˇŁÄĄÎϤϾď¤Ë¸ą¤ÎĘý¸ţ¤ËĆŻ¤ŻˇŁ¶Ę¤¬¤Ă¤żľőÂ֤ˤ˘¤ë¸ą¤ÎČů
ľ®Éôʬ¤ňąÍ¤¨¤ë¤Čˇ˘ÎľĘý¤«¤é¤ÎÄĄÎĎ
¤ÎąçÎϤϸą¤Î¶Ę¤¬¤ę¤ň˛ňľĂ¤·¤č¤¦¤Č¤ą¤ëĘý¸ţ¤Ë¸ţ¤ŻˇŁ¤Ţ¤Ă¤ą¤°¤ĘľőÂ֤ˤʤë¤Čˇ˘¸ą¤Ë¤ĎÁ´ÂΤȤ·¤Ć¤ĎÎϤ¬ĆŻ¤«¤Ę¤Ż¤Ę¤ëˇŁ¤ć¤¨¤Ëˇ˘¸ą¤Ď¤Ţ¤Ă¤ą¤°¤Ë¤Ę¤í¤¦¤Č¤ą¤ë
ˇĘ¤Ä¤Ţ¤ęˇÖÉü¸µÎϤň»ý¤Äˇ×ˇËˇŁżĺĚ̤ˤǤ¤ëÇȤâƱÍͤǡ˘˛ż¤«¤Î¸¶°ř¤ÇżĺĚ̤ËŔą¤ęľĺ¤¬¤Ă¤ż¤ę¤Ż¤Ü¤ó¤Ŕ¤ę¤·¤Ć¤¤¤ëÉôʬ¤¬¤˘¤ë¤Čˇ˘Ŕą¤ęľĺ¤¬¤Ă¤żÉôʬ¤ň˛Ľ¤˛ˇ˘¤Ż¤Ü
¤ó¤ŔÉôʬ¤ňľĺ¤˛¤ë¤č¤¦¤Ëżĺ¤¬°ÜĆ°¤ą¤ëˇŁ¸ą¤Îż¶Ć°¤Ç¤âżĺĚ̤ǤⶦÄ̤ą¤ëÂç»ö¤Ę¤ł¤Č¤ĎˇÖ¶ő´ÖĹŞ¤ĘĘѲ˝¤¬»ţ´ÖĹŞĘѲ˝¤ňŔ¸¤ŕˇ×¤Č¤¤¤¦ĘŞÍý¸˝ľÝ¤¬ˇÖÇȤÎĹÁÇšפȤ¤¤¦
¸˝ľÝ¤ň°ú¤µŻ¤ł¤·¤Ć¤¤¤ë¤Č¤¤¤¦¤ł¤Č¤Ç¤˘¤ëˇŁĽ«Áłł¦¤Ë¤Ďˇ˘˛ż¤«¤ËÉÔÄŕ¤ęąç¤¤¤¬¤˘¤ë¤Č¤˝¤ě¤ňŔµ¤˝¤¦¤Č¤ą¤ëÎϤ¬ĆŻ¤Ż¤č¤¦¤Çˇ˘¤˝¤ÎÎϤˤč¤ęż¶Ć°¤äÇȤ¬ČŻŔ¸¤ą¤ëˇŁĽ«
Áłł¦¤Î¤˘¤Á¤ł¤Á¤ÇˇÖÇȡפ¬ČŻŔ¸¤ą¤ë¤Î¤Ď¤˝¤Î¤Ş¤«¤˛¤Ç¤˘¤ëˇŁ
ˇˇ¤ą¤Ç¤Ë˝Ň¤Ů¤ż¤č¤¦¤Ëˇ˘ĹĹĽ§µ¤¤Ë¤Ä¤¤¤Ć¤âˇ˘Ć±¤¸¸¶Â§¤¬Ŕ®Î©¤·¤Ć¤¤¤ëˇŁ¤č¤Ă¤Ćˇ˘ˇÖÇȤηÁ¤ň¤·¤Ć¤¤¤ë¤¬ż¶Ć°¤·¤Ę¤¤ĹĹĽ§ľěˇ×¤Č¤¤¤¦¤Î¤Ďˇ˘ˇÖξü¤ň°ú¤ĂÄĄ¤é¤ě¤Ć¤¤
¤ë¤Î¤Ëˇ˘¶Ę¤¬¤Ă¤ż¤Ţ¤Ţ¤ÇÄľŔţ¤ËĚá¤í¤¦¤Č¤·¤Ę¤¤¸ąˇ×¤äˇÖ°ěÉô¤¬¤¤¤Ä¤Ţ¤Ç¤âŔą¤ęľĺ¤¬¤Ă¤ż¤Ţ¤Ţˇ˘Ęř¤ě¤â¤·¤Ę¤¤żĺĚ̡פČƱ¤¸¤°¤é¤¤ÉԻ׵Ĥʸ˝ľÝ¤Ę¤Î¤Ç¤˘¤ëˇŁ18şĐ
¤ÎĄ˘Ą¤ĄóĄ·ĄĺĄżĄ¤Ąó¤ňÇş¤Ţ¤»¤ż¤Î¤âÉԻ׵ĤǤϤʤ¤ˇŁ
ˇˇ¤µ¤Ćˇ˘¸÷®Ĺ٤ÇÁö¤ëżÍ¤«¤é¸«¤żĹĹĽ§ÇȤÎĚäÂę¤ËĚá¤ęˇ˘¤č¤ę¶ńÂÎĹŞ¤ËˇÖ»ß¤Ţ¤Ă¤żĹĹĽ§ÇȤϤ˘¤ęĆŔ¤Ę¤¤ˇ×¤ł¤Č¤ňłÎǧ¤·¤Ć¤Ş¤ł¤¦ˇŁĹĹĽ§ÇȤň®ĹŮc¤ÇÁö¤ę¤Ę¤¬¤é¸«¤ż
¤Č¤ą¤ë¤Čˇ˘¤˝¤Î´Ń¬ĽÔ¤Ë¤Č¤Ă¤Ć¤ÎşÂɸ·Ď(X,T)¤Ď®ĹŮc¤Ç¤ÎĄ¬ĄęĄěĄ¤ĘŃ´ą¤ň»Ü¤·¤żşÂɸ·Ď
ˇˇ¸ą¤Îż¶Ć°¤Îľěąç¤ňąÍ¤¨¤ëˇŁĄÔĄó¤ČÄĄ¤é¤ě¤ż¸ą¤Ë¤ĎÄĄÎϤ¬ĆŻ¤¤¤Ć¤¤¤ëˇŁÄĄÎϤϾď¤Ë¸ą¤ÎĘý¸ţ¤ËĆŻ¤ŻˇŁ¶Ę¤¬¤Ă¤żľőÂ֤ˤ˘¤ë¸ą¤ÎČů
ľ®Éôʬ¤ňąÍ¤¨¤ë¤Čˇ˘ÎľĘý¤«¤é¤ÎÄĄÎĎ
¤ÎąçÎϤϸą¤Î¶Ę¤¬¤ę¤ň˛ňľĂ¤·¤č¤¦¤Č¤ą¤ëĘý¸ţ¤Ë¸ţ¤ŻˇŁ¤Ţ¤Ă¤ą¤°¤ĘľőÂ֤ˤʤë¤Čˇ˘¸ą¤Ë¤ĎÁ´ÂΤȤ·¤Ć¤ĎÎϤ¬ĆŻ¤«¤Ę¤Ż¤Ę¤ëˇŁ¤ć¤¨¤Ëˇ˘¸ą¤Ď¤Ţ¤Ă¤ą¤°¤Ë¤Ę¤í¤¦¤Č¤ą¤ë
ˇĘ¤Ä¤Ţ¤ęˇÖÉü¸µÎϤň»ý¤Äˇ×ˇËˇŁżĺĚ̤ˤǤ¤ëÇȤâƱÍͤǡ˘˛ż¤«¤Î¸¶°ř¤ÇżĺĚ̤ËŔą¤ęľĺ¤¬¤Ă¤ż¤ę¤Ż¤Ü¤ó¤Ŕ¤ę¤·¤Ć¤¤¤ëÉôʬ¤¬¤˘¤ë¤Čˇ˘Ŕą¤ęľĺ¤¬¤Ă¤żÉôʬ¤ň˛Ľ¤˛ˇ˘¤Ż¤Ü
¤ó¤ŔÉôʬ¤ňľĺ¤˛¤ë¤č¤¦¤Ëżĺ¤¬°ÜĆ°¤ą¤ëˇŁ¸ą¤Îż¶Ć°¤Ç¤âżĺĚ̤ǤⶦÄ̤ą¤ëÂç»ö¤Ę¤ł¤Č¤ĎˇÖ¶ő´ÖĹŞ¤ĘĘѲ˝¤¬»ţ´ÖĹŞĘѲ˝¤ňŔ¸¤ŕˇ×¤Č¤¤¤¦ĘŞÍý¸˝ľÝ¤¬ˇÖÇȤÎĹÁÇšפȤ¤¤¦
¸˝ľÝ¤ň°ú¤µŻ¤ł¤·¤Ć¤¤¤ë¤Č¤¤¤¦¤ł¤Č¤Ç¤˘¤ëˇŁĽ«Áłł¦¤Ë¤Ďˇ˘˛ż¤«¤ËÉÔÄŕ¤ęąç¤¤¤¬¤˘¤ë¤Č¤˝¤ě¤ňŔµ¤˝¤¦¤Č¤ą¤ëÎϤ¬ĆŻ¤Ż¤č¤¦¤Çˇ˘¤˝¤ÎÎϤˤč¤ęż¶Ć°¤äÇȤ¬ČŻŔ¸¤ą¤ëˇŁĽ«
Áłł¦¤Î¤˘¤Á¤ł¤Á¤ÇˇÖÇȡפ¬ČŻŔ¸¤ą¤ë¤Î¤Ď¤˝¤Î¤Ş¤«¤˛¤Ç¤˘¤ëˇŁ
ˇˇ¤ą¤Ç¤Ë˝Ň¤Ů¤ż¤č¤¦¤Ëˇ˘ĹĹĽ§µ¤¤Ë¤Ä¤¤¤Ć¤âˇ˘Ć±¤¸¸¶Â§¤¬Ŕ®Î©¤·¤Ć¤¤¤ëˇŁ¤č¤Ă¤Ćˇ˘ˇÖÇȤηÁ¤ň¤·¤Ć¤¤¤ë¤¬ż¶Ć°¤·¤Ę¤¤ĹĹĽ§ľěˇ×¤Č¤¤¤¦¤Î¤Ďˇ˘ˇÖξü¤ň°ú¤ĂÄĄ¤é¤ě¤Ć¤¤
¤ë¤Î¤Ëˇ˘¶Ę¤¬¤Ă¤ż¤Ţ¤Ţ¤ÇÄľŔţ¤ËĚá¤í¤¦¤Č¤·¤Ę¤¤¸ąˇ×¤äˇÖ°ěÉô¤¬¤¤¤Ä¤Ţ¤Ç¤âŔą¤ęľĺ¤¬¤Ă¤ż¤Ţ¤Ţˇ˘Ęř¤ě¤â¤·¤Ę¤¤żĺĚ̡פČƱ¤¸¤°¤é¤¤ÉԻ׵Ĥʸ˝ľÝ¤Ę¤Î¤Ç¤˘¤ëˇŁ18şĐ
¤ÎĄ˘Ą¤ĄóĄ·ĄĺĄżĄ¤Ąó¤ňÇş¤Ţ¤»¤ż¤Î¤âÉԻ׵ĤǤϤʤ¤ˇŁ
ˇˇ¤µ¤Ćˇ˘¸÷®Ĺ٤ÇÁö¤ëżÍ¤«¤é¸«¤żĹĹĽ§ÇȤÎĚäÂę¤ËĚá¤ęˇ˘¤č¤ę¶ńÂÎĹŞ¤ËˇÖ»ß¤Ţ¤Ă¤żĹĹĽ§ÇȤϤ˘¤ęĆŔ¤Ę¤¤ˇ×¤ł¤Č¤ňłÎǧ¤·¤Ć¤Ş¤ł¤¦ˇŁĹĹĽ§ÇȤň®ĹŮc¤ÇÁö¤ę¤Ę¤¬¤é¸«¤ż
¤Č¤ą¤ë¤Čˇ˘¤˝¤Î´Ń¬ĽÔ¤Ë¤Č¤Ă¤Ć¤ÎşÂɸ·Ď(X,T)¤Ď®ĹŮc¤Ç¤ÎĄ¬ĄęĄěĄ¤ĘŃ´ą¤ň»Ü¤·¤żşÂɸ·Ď
|
(3.3) |
|
(3.4) |
 ˇˇÂč1ľĎ¤ÇłµÍפŔ¤±˝Ň¤Ů¤żˇ˘ĹĹĽ§Í¶Ćł¤Ë´Ř¤ą¤ëµżĚä¤Ë¤Ä¤¤¤Ćˇ˘¤ł¤ł¤Ç¤Ż¤ď¤·¤ŻąÍ¤¨¤Ć¤Ş
¤ł¤¦ˇŁżŢ¤Î¤č¤¦¤Ëˇ˘Ćó¤Ä¤Î¸˝ľÝ¤ňąÍ¤¨¤ëˇŁş¸¤ÎżŢ¤Ç¤Ďˇ˘ĄłĄ¤Ąë¤¬Ľ§ŔФ˶á¤Ĺ¤ˇ˘±¦¤ÎżŢ¤Ç¤Ďˇ˘Ľ§ŔФ¬ĄłĄ¤Ąë¤Ë¶á¤Ĺ¤ŻˇŁĆó¤Ä¤Î¸˝ľÝ¤Ďˇ˘¸«¤ëΩľě¤ňĘѤ¨¤ě¤ĐƱ¤¸¸˝
ľÝ¤Ç¤˘¤ęˇ˘·ë˛Ě¤Č¤·¤ĆˇÖĄłĄ¤Ąë¤Ë»ţ·×¤Ţ¤ď¤ę¤ÎĹĹή¤¬Î®¤ě¤ëˇ×¤Č¤¤¤¦ĹŔ¤Ç¤âƱ¤¸¤Ç¤˘¤ëˇŁ¤·¤«¤·ˇ˘¤˝¤Îµ˝Ň¤ĎƱ¤¸¤Ç¤Ď¤Ę¤¤ˇŁ
±¦żŢ¤Îľěąç¤Ç¤˘¤ě¤Đˇ˘¤˝¤ě¤ĎĄłĄ¤ĄëĆâ¤ÎĽ§Â«Ě©Ĺ٤¬»ţ´ÖĘѲ˝¤ą¤ë¤Č¤¤¤¦¤ł¤Č¤«¤é¤Ż¤ë¤Č˛ňĽá¤µ¤ě¤ëˇŁ¤ą¤Ę¤ď¤ÁMaxwellĘýÄřĽ°¤Îrot˘ŞE = ˇÝ[(˘ß˘ŞB)/˘ßt]
¤Ë¤·¤ż¤¬¤Ă¤Ćˇ˘Ľ§Â«Ě©Ĺ٤¬ĘѲ˝¤·¤Ć¤¤¤ëľě˝ę¤Ë¤ĎĹĹľě¤Î±˛¤¬ČŻŔ¸¤·¤Ć¤¤¤Ćˇ˘¤˝¤ÎĹĹľě¤Ë¤č¤Ă¤ĆĄłĄ¤ĄëĂć¤ÎĹŻҤ¬ÎϤňĽő¤±ˇ˘ĹĹή¤Č¤Ę¤ëˇŁ¤č¤ŻĂΤé¤ě¤Ć¤¤¤ë¤č¤¦
¤Ëˇ˘¤ł¤Î»ţ¤ËČŻŔ¸¤ą¤ëĹĹ°Ěşą¤Ďˇ˘ĄŐĄˇĄéĄÇˇĽ¤ÎĹĹĽ§Í¶Ćł¤Îˡ§V=ˇÝ[d¦µ/dt]¤Ë¤č¤Ă¤Ćµá¤á¤é¤ě¤ëˇŁ¤ł¤ł¤Ç¦µ¤Ď˛óĎ©Ćâ¤ň¤Ä¤é¤Ě¤ŻĽ§Â«¤Ç¤˘¤ęˇ˘V¤ÎÉäąć¤Ď
¦µ¤ËÂФ·¤Ć±¦ĄÍĄ¸¤Î¸ţ¤¤ËĹĹή¤ňή¤˝¤¦¤Č¤ą¤ë»ţ¤ËĄ×ĄéĄą¤ČÄęµÁ¤µ¤ě¤ë23ˇŁ
ˇˇÂč1ľĎ¤ÇłµÍפŔ¤±˝Ň¤Ů¤żˇ˘ĹĹĽ§Í¶Ćł¤Ë´Ř¤ą¤ëµżĚä¤Ë¤Ä¤¤¤Ćˇ˘¤ł¤ł¤Ç¤Ż¤ď¤·¤ŻąÍ¤¨¤Ć¤Ş
¤ł¤¦ˇŁżŢ¤Î¤č¤¦¤Ëˇ˘Ćó¤Ä¤Î¸˝ľÝ¤ňąÍ¤¨¤ëˇŁş¸¤ÎżŢ¤Ç¤Ďˇ˘ĄłĄ¤Ąë¤¬Ľ§ŔФ˶á¤Ĺ¤ˇ˘±¦¤ÎżŢ¤Ç¤Ďˇ˘Ľ§ŔФ¬ĄłĄ¤Ąë¤Ë¶á¤Ĺ¤ŻˇŁĆó¤Ä¤Î¸˝ľÝ¤Ďˇ˘¸«¤ëΩľě¤ňĘѤ¨¤ě¤ĐƱ¤¸¸˝
ľÝ¤Ç¤˘¤ęˇ˘·ë˛Ě¤Č¤·¤ĆˇÖĄłĄ¤Ąë¤Ë»ţ·×¤Ţ¤ď¤ę¤ÎĹĹή¤¬Î®¤ě¤ëˇ×¤Č¤¤¤¦ĹŔ¤Ç¤âƱ¤¸¤Ç¤˘¤ëˇŁ¤·¤«¤·ˇ˘¤˝¤Îµ˝Ň¤ĎƱ¤¸¤Ç¤Ď¤Ę¤¤ˇŁ
±¦żŢ¤Îľěąç¤Ç¤˘¤ě¤Đˇ˘¤˝¤ě¤ĎĄłĄ¤ĄëĆâ¤ÎĽ§Â«Ě©Ĺ٤¬»ţ´ÖĘѲ˝¤ą¤ë¤Č¤¤¤¦¤ł¤Č¤«¤é¤Ż¤ë¤Č˛ňĽá¤µ¤ě¤ëˇŁ¤ą¤Ę¤ď¤ÁMaxwellĘýÄřĽ°¤Îrot˘ŞE = ˇÝ[(˘ß˘ŞB)/˘ßt]
¤Ë¤·¤ż¤¬¤Ă¤Ćˇ˘Ľ§Â«Ě©Ĺ٤¬ĘѲ˝¤·¤Ć¤¤¤ëľě˝ę¤Ë¤ĎĹĹľě¤Î±˛¤¬ČŻŔ¸¤·¤Ć¤¤¤Ćˇ˘¤˝¤ÎĹĹľě¤Ë¤č¤Ă¤ĆĄłĄ¤ĄëĂć¤ÎĹŻҤ¬ÎϤňĽő¤±ˇ˘ĹĹή¤Č¤Ę¤ëˇŁ¤č¤ŻĂΤé¤ě¤Ć¤¤¤ë¤č¤¦
¤Ëˇ˘¤ł¤Î»ţ¤ËČŻŔ¸¤ą¤ëĹĹ°Ěşą¤Ďˇ˘ĄŐĄˇĄéĄÇˇĽ¤ÎĹĹĽ§Í¶Ćł¤Îˡ§V=ˇÝ[d¦µ/dt]¤Ë¤č¤Ă¤Ćµá¤á¤é¤ě¤ëˇŁ¤ł¤ł¤Ç¦µ¤Ď˛óĎ©Ćâ¤ň¤Ä¤é¤Ě¤ŻĽ§Â«¤Ç¤˘¤ęˇ˘V¤ÎÉäąć¤Ď
¦µ¤ËÂФ·¤Ć±¦ĄÍĄ¸¤Î¸ţ¤¤ËĹĹή¤ňή¤˝¤¦¤Č¤ą¤ë»ţ¤ËĄ×ĄéĄą¤ČÄęµÁ¤µ¤ě¤ë23ˇŁ
|
|
|
(3.5) |
|
(3.6) |
|
(3.7) |
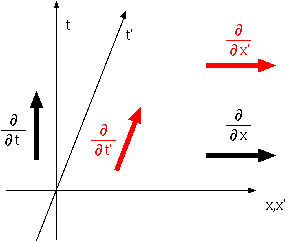 ˇˇ
¤Ä¤Ţ¤ęˇ˘x¤Ë¤č¤ëČůʬ¤Čxˇě¤Ë¤č¤ëČůʬ¤ĎƱ¤¸¤â¤Î¤Çˇ˘t¤Ë¤č¤ëČůʬ¤Čtˇě¤Ë¤č¤ëČůʬ¤¬ĘѲ˝¤ą¤ëˇŁşÂɸ¤Ďx¤¬ĘѲ˝¤·¤Ćt¤ĎĘѲ˝¤·¤Ć¤¤¤Ę¤¤¤Î¤Ŕ¤«¤éˇ˘´ńĚŻ¤Ë
»×¤¨¤ë¤«¤â¤·¤ě¤Ę¤¤ˇŁ¤·¤«¤·[˘ß/˘ßt] ˇâ
[˘ß/˘ßtˇě]¤Ç¤˘¤ë¤ł¤Č¤Ďˇ˘[˘ß/˘ßt]¤¬ˇÖx¤ň°ěÄę¤Č¤·¤Ćt¤ÇČůʬˇ×¤Ç¤˘¤ęˇ˘[˘ß/˘ßtˇě]¤¬ˇÖxˇě¤ň°ěÄę¤Č¤·¤Ćtˇě¤ÇČůʬˇ×¤Ç¤˘¤ë¤ł¤Č¤ňąÍ¤¨¤ě¤Đˇ˘
ÇĽĆŔ¤¬¤¤¤Ż¤Ŕ¤í¤¦ˇŁľĺżŢ¤«¤é¤ď¤«¤ë¤č¤¦¤Ëˇ˘ˇÖx°ěÄę¤Č¤·¤Ćt¤¬ĘѲ˝¤ą¤ëˇ×ľěąç¤ČˇÖxˇě°ěÄę¤Č¤·¤Ćtˇě¤¬ĘѲ˝ˇ×¤ą¤ëľěąç¤Ç¤Ď°ÜĆ°Ęý¸ţ¤¬°ă¤¦¤Î¤Ç¤˘¤ëˇŁ
ˇˇµŐ¤Ëˇ˘[˘ß/˘ßx]¤¬ˇÖt¤ň°ěÄę¤Č¤·¤Ćx¤ÇČůʬˇ×¤Ç¤˘¤ęˇ˘[˘ß/˘ßxˇě]¤¬ˇÖtˇě¤ň°ěÄę¤Č¤·¤Ćxˇě¤ÇČůʬˇ×¤Ç¤˘¤ë¤ł¤Č¤ňąÍ¤¨¤ě¤Đˇ˘¤ł¤ÎĆó¤Ä¤ĎƱ¤¸¤â¤Î¤Ç
¤˘¤ë¤ł¤Č¤âÇĽĆŔ¤Ç¤¤ëˇŁ
ˇˇ
¤Ä¤Ţ¤ęˇ˘x¤Ë¤č¤ëČůʬ¤Čxˇě¤Ë¤č¤ëČůʬ¤ĎƱ¤¸¤â¤Î¤Çˇ˘t¤Ë¤č¤ëČůʬ¤Čtˇě¤Ë¤č¤ëČůʬ¤¬ĘѲ˝¤ą¤ëˇŁşÂɸ¤Ďx¤¬ĘѲ˝¤·¤Ćt¤ĎĘѲ˝¤·¤Ć¤¤¤Ę¤¤¤Î¤Ŕ¤«¤éˇ˘´ńĚŻ¤Ë
»×¤¨¤ë¤«¤â¤·¤ě¤Ę¤¤ˇŁ¤·¤«¤·[˘ß/˘ßt] ˇâ
[˘ß/˘ßtˇě]¤Ç¤˘¤ë¤ł¤Č¤Ďˇ˘[˘ß/˘ßt]¤¬ˇÖx¤ň°ěÄę¤Č¤·¤Ćt¤ÇČůʬˇ×¤Ç¤˘¤ęˇ˘[˘ß/˘ßtˇě]¤¬ˇÖxˇě¤ň°ěÄę¤Č¤·¤Ćtˇě¤ÇČůʬˇ×¤Ç¤˘¤ë¤ł¤Č¤ňąÍ¤¨¤ě¤Đˇ˘
ÇĽĆŔ¤¬¤¤¤Ż¤Ŕ¤í¤¦ˇŁľĺżŢ¤«¤é¤ď¤«¤ë¤č¤¦¤Ëˇ˘ˇÖx°ěÄę¤Č¤·¤Ćt¤¬ĘѲ˝¤ą¤ëˇ×ľěąç¤ČˇÖxˇě°ěÄę¤Č¤·¤Ćtˇě¤¬ĘѲ˝ˇ×¤ą¤ëľěąç¤Ç¤Ď°ÜĆ°Ęý¸ţ¤¬°ă¤¦¤Î¤Ç¤˘¤ëˇŁ
ˇˇµŐ¤Ëˇ˘[˘ß/˘ßx]¤¬ˇÖt¤ň°ěÄę¤Č¤·¤Ćx¤ÇČůʬˇ×¤Ç¤˘¤ęˇ˘[˘ß/˘ßxˇě]¤¬ˇÖtˇě¤ň°ěÄę¤Č¤·¤Ćxˇě¤ÇČůʬˇ×¤Ç¤˘¤ë¤ł¤Č¤ňąÍ¤¨¤ě¤Đˇ˘¤ł¤ÎĆó¤Ä¤ĎƱ¤¸¤â¤Î¤Ç
¤˘¤ë¤ł¤Č¤âÇĽĆŔ¤Ç¤¤ëˇŁ
|
|
(3.8) |
|
(3.9) |
|
(3.10) |
|
(3.11) |
|
(3.12) |
|
(3.13) |
|
(3.14) |
|
(3.15) |
|
(3.16) |
|
(3.17) |
|
(3.18) |
|
(3.19) |
|
(3.20) |
|
|
 ĄŘĄëĄÄ¤ÎĘýÄřĽ°¤¬Ŕµ¤·¤¤¤«¤É¤¦¤«¤ňČ˝Äę¤Ç¤¤ëĽÂ¸ł¤Č¤·¤Ćˇ˘ĄěĄóĄČĄ˛Ąó(RŹ«Óntgen)¤ČĄ˘Ą¤ĄŐĄ§ĄóĄôĄˇĄëĄČ(Eichenward)¤Ë¤č¤ëˇ˘˛óĹľ¤ą¤ëͶ
ĹĹÂΤμ¸ł¤¬¤˘¤ëˇŁżŢ¤Î¤č¤¦¤ËͶĹĹÂΤňČľ·ÂR¤Î±ßĹű·Á¤Ë¤·¤Ćˇ˘Ľ´Ęý¸ţ¤ËĽ§ľě¤ň¤«¤±¤Ć¤Ş¤¤¤Ć˛óĹľ¤µ¤»¤ëˇŁ
Ą¨ˇĽĄĆĄë¤¬¤ł¤Î˛óĹľ¤ą¤ëͶĹĹÂΤȰě˝ď¤Ë±żĆ°¤·¤Ć¤¤¤ë¤Č¤ą¤ě¤Đˇ˘ĄŘĄëĄÄ¤ÎĘýÄřĽ°¤ÎĂć¤Î˘Şv¤Ë
¤Ďˇ˘łĆĹŔłĆĹŔ¤Î˛óž®Ĺ٤ňÂĺĆţ¤ą¤ě¤Đ¤č¤¤(¤ł¤ě¤ÇËÜĹö¤Ë¤¤¤¤¤Î¤«¤ĎşĆąÍ¤¬É¬Í×)ˇŁĽ§ľě¤¬°ěÄę¤Ŕ¤Č¤·¤ĆĄŘĄëĄÄ¤ÎĘýÄřĽ°(3.17)¤Ď¤ł¤Îľěąçˇ˘
ĄŘĄëĄÄ¤ÎĘýÄřĽ°¤¬Ŕµ¤·¤¤¤«¤É¤¦¤«¤ňČ˝Äę¤Ç¤¤ëĽÂ¸ł¤Č¤·¤Ćˇ˘ĄěĄóĄČĄ˛Ąó(RŹ«Óntgen)¤ČĄ˘Ą¤ĄŐĄ§ĄóĄôĄˇĄëĄČ(Eichenward)¤Ë¤č¤ëˇ˘˛óĹľ¤ą¤ëͶ
ĹĹÂΤμ¸ł¤¬¤˘¤ëˇŁżŢ¤Î¤č¤¦¤ËͶĹĹÂΤňČľ·ÂR¤Î±ßĹű·Á¤Ë¤·¤Ćˇ˘Ľ´Ęý¸ţ¤ËĽ§ľě¤ň¤«¤±¤Ć¤Ş¤¤¤Ć˛óĹľ¤µ¤»¤ëˇŁ
Ą¨ˇĽĄĆĄë¤¬¤ł¤Î˛óĹľ¤ą¤ëͶĹĹÂΤȰě˝ď¤Ë±żĆ°¤·¤Ć¤¤¤ë¤Č¤ą¤ě¤Đˇ˘ĄŘĄëĄÄ¤ÎĘýÄřĽ°¤ÎĂć¤Î˘Şv¤Ë
¤Ďˇ˘łĆĹŔłĆĹŔ¤Î˛óž®Ĺ٤ňÂĺĆţ¤ą¤ě¤Đ¤č¤¤(¤ł¤ě¤ÇËÜĹö¤Ë¤¤¤¤¤Î¤«¤ĎşĆąÍ¤¬É¬Í×)ˇŁĽ§ľě¤¬°ěÄę¤Ŕ¤Č¤·¤ĆĄŘĄëĄÄ¤ÎĘýÄřĽ°(3.17)¤Ď¤ł¤Îľěąçˇ˘
|
(3.21) |
|
(3.22) |
 ľĺ¤ÇĹĹľěĂć¤ÇĘŞÂΤň˛óĹľ¤µ¤»¤ĆĽ§ľě¤ňşî¤Ă¤ż¤ł¤Č¤ÎµŐ¤Çˇ˘ĘŞÂΤňĽ§ľěĂć¤Ç˛óĹľ¤µ¤»¤Ćʬ¶Ë¤ňşî¤ëĽÂ¸ł¤¬¤˘¤ëˇŁ¤ł¤Î¸˝ľÝ¤Ë¤Ä¤¤¤Ć¤Ďˇ˘Ą˘Ą¤ĄóĄ·ĄĺĄżĄ¤Ąó¤ČĄéĄ¦Ą×¤¬
ĄíˇĽĄěĄóĄÄĘŃ´ą¤ň»Č¤Ă¤ĆĽ§ľěĂć¤ÇĆ°¤ŻĽ§ŔÂΤÎʬ¶Ë¤ň·×»»¤·¤Ć¤¤¤ë(1908ÇŻ)ˇŁW.Ą¦ĄŁĄëĄ˝Ąó¤ČH.A.Ą¦ĄŁĄëĄ˝Ąó¤¬ĽÂ¸ł¤ÇłÎǧ¤·¤ż(1913ÇŻ)ˇŁ¤ł
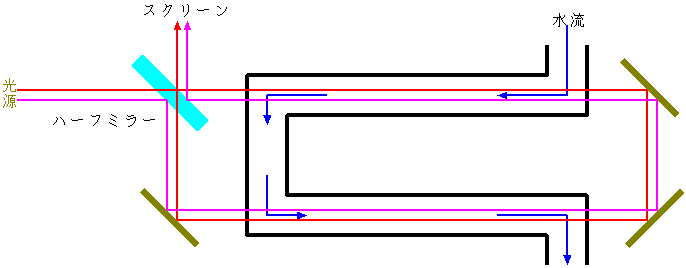
¤ÎĽÂ¸ł·ë˛Ě¤âˇ˘ÁÇËѤ˥إëĄÄ¤ÎĘýÄřĽ°¤ňŬÍѤ·¤ż·×»»¤Č¤Ďąç¤ď¤Ę¤¤¤¬ˇ˘ÁęÂĐĎŔĹŞ·×»»¤Ę¤é¤Đąç¤¦ˇŁ
¤ł¤ł¤Ç¤ĎˇÖͶĹĹÂΤ¬˛óĹľ¤·¤Ć¤¤¤ë®Ĺ٤ňĄŘĄëĄÄ¤ÎĘýÄřĽ°¤Î˘Şv¤ËÂĺĆţ¤ą¤ëˇ×¤Č¤¤¤¦·×»»¤ň¤ä¤Ă
¤Ć¤¤¤ë¤¬ˇ˘ĘŞÂΤ¬Ć°¤¤¤Ć¤â¤˝¤Îľě˝ę¤ÎĄ¨ˇĽĄĆĄë¤ĎĆ°¤«¤Ę¤¤¤Î¤«¤â¤·¤ě¤Ę¤¤ˇŁĽÂ¤ĎˇÖĘŞÂΤ¬Ć°¤Ż¤Č¤˝¤ÎĽţ¤ę¤ÎĄ¨ˇĽĄĆĄë¤Ď°ě˝ď¤ËĆ°¤Ż¤Î¤«ˇ©ˇ×¤Č¤¤¤¦¤ł¤Č¤ňÄę¤á¤ë¤ż
¤á¤ÎĽÂ¸ł¤Ďˇ˘¤ą¤Ç¤Ë1851ÇŻ¤ËĄŐĄŁĄľˇĽ(Fizeau)¤Ë¤č¤Ă¤Ć¤Ę¤µ¤ě¤Ć¤¤¤ëˇŁ
ľĺ¤ÇĹĹľěĂć¤ÇĘŞÂΤň˛óĹľ¤µ¤»¤ĆĽ§ľě¤ňşî¤Ă¤ż¤ł¤Č¤ÎµŐ¤Çˇ˘ĘŞÂΤňĽ§ľěĂć¤Ç˛óĹľ¤µ¤»¤Ćʬ¶Ë¤ňşî¤ëĽÂ¸ł¤¬¤˘¤ëˇŁ¤ł¤Î¸˝ľÝ¤Ë¤Ä¤¤¤Ć¤Ďˇ˘Ą˘Ą¤ĄóĄ·ĄĺĄżĄ¤Ąó¤ČĄéĄ¦Ą×¤¬
ĄíˇĽĄěĄóĄÄĘŃ´ą¤ň»Č¤Ă¤ĆĽ§ľěĂć¤ÇĆ°¤ŻĽ§ŔÂΤÎʬ¶Ë¤ň·×»»¤·¤Ć¤¤¤ë(1908ÇŻ)ˇŁW.Ą¦ĄŁĄëĄ˝Ąó¤ČH.A.Ą¦ĄŁĄëĄ˝Ąó¤¬ĽÂ¸ł¤ÇłÎǧ¤·¤ż(1913ÇŻ)ˇŁ¤ł
¤ÎĽÂ¸ł·ë˛Ě¤âˇ˘ÁÇËѤ˥إëĄÄ¤ÎĘýÄřĽ°¤ňŬÍѤ·¤ż·×»»¤Č¤Ďąç¤ď¤Ę¤¤¤¬ˇ˘ÁęÂĐĎŔĹŞ·×»»¤Ę¤é¤Đąç¤¦ˇŁ
¤ł¤ł¤Ç¤ĎˇÖͶĹĹÂΤ¬˛óĹľ¤·¤Ć¤¤¤ë®Ĺ٤ňĄŘĄëĄÄ¤ÎĘýÄřĽ°¤Î˘Şv¤ËÂĺĆţ¤ą¤ëˇ×¤Č¤¤¤¦·×»»¤ň¤ä¤Ă
¤Ć¤¤¤ë¤¬ˇ˘ĘŞÂΤ¬Ć°¤¤¤Ć¤â¤˝¤Îľě˝ę¤ÎĄ¨ˇĽĄĆĄë¤ĎĆ°¤«¤Ę¤¤¤Î¤«¤â¤·¤ě¤Ę¤¤ˇŁĽÂ¤ĎˇÖĘŞÂΤ¬Ć°¤Ż¤Č¤˝¤ÎĽţ¤ę¤ÎĄ¨ˇĽĄĆĄë¤Ď°ě˝ď¤ËĆ°¤Ż¤Î¤«ˇ©ˇ×¤Č¤¤¤¦¤ł¤Č¤ňÄę¤á¤ë¤ż
¤á¤ÎĽÂ¸ł¤Ďˇ˘¤ą¤Ç¤Ë1851ÇŻ¤ËĄŐĄŁĄľˇĽ(Fizeau)¤Ë¤č¤Ă¤Ć¤Ę¤µ¤ě¤Ć¤¤¤ëˇŁ
|
(3.23) |
|