高階微分
導関数の導関数
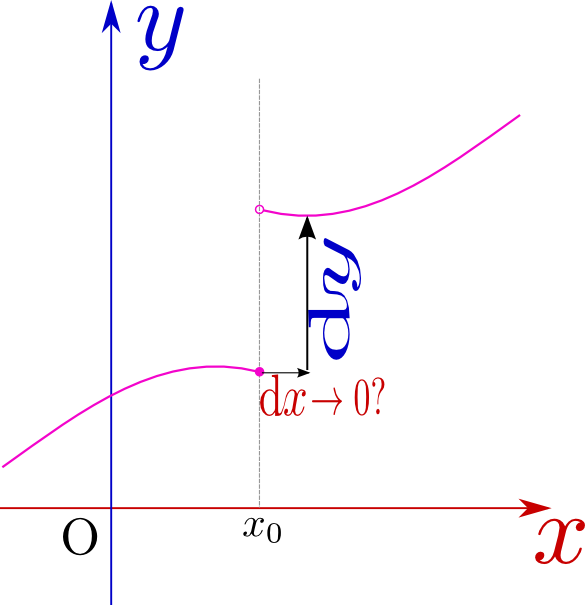
導関数$f'({x})=\lim_{{\Delta x}\to0}{f({x}+{\Delta x})-f({x})\over {\Delta x}}$の導関数、つまり
\begin{equation} f''({x})=\lim_{{\Delta x}\to0}{f'({x}+{\Delta x})-f'({x})\over {\Delta x}} \end{equation}を作ってみよう。これを「二階微分」非常に頻繁に「二回微分」と書く人がいるが、これは誤字である(しかし発音では区別がつかないから安心だ)。と呼び、記号としては$'$を重ねて$f''({x})$と表現することにしよう($f({x})\to f'({x})$が「一階微分」、$f({x})\to f'({x})\to f''({x})$が「二階微分」である)。また、一階微分を${\mathrm d \over \mathrm dx }f({x})$と書いたように、二階微分は
\begin{equation} f''({x})= {\mathrm d \over \mathrm dx }\left( {\mathrm d \over \mathrm dx }f({x}) \right)= {\mathrm d ^2\over \mathrm dx ^2} f({x})={\mathrm d^2 f\over \mathrm dx ^2}({x})\label{nikai} \end{equation}と表現してもよい。
同様に三階微分や四階微分も定義されるが、数が大きくなった時は(十階微分を$f^{\prime\prime\prime\prime\prime\prime\prime\prime\prime\prime}({x})$などと書くのは不経済なので)$n$階微分は$f^{(n)}({x})$と表現する$\left(f''({x})={\mathrm d ^2\over \mathrm dx ^2}f({x})=f^{(2)}({x})\right)$。
二階微分がどんな意味を持つかを考えよう。二次関数や三次関数の形を考えたときに、1次の項${x}$の係数が原点における傾きを、2次の項${x}^2$の係数が原点における「曲がり具合」を表現していたのを覚えているだろうか。その考え方からすると、二階微分の値は「曲線の曲がり具合」を表現することになる。
定義式から二階微分を計算することで、確かに「曲がり具合」であることを確認しよう。まず、$ f''({x})=\lim_{{\Delta x}\to0}{f'({x}+{\Delta x})-f'({x})\over {\Delta x}}$という二階微分の意味を表した式そのものに、一階微分の式$\lim_{{\Delta x}\to0}{f({x}+{\Delta x})-f({x})\over {\Delta x}}$を代入する。
\begin{equation} \begin{array}{rll} f''({x}) =&\lim_{{\Delta x}\to0}{\overbrace{ {f({x}+{\Delta x}+{\Delta x})-f({x}+{\Delta x})\over {\Delta x}}}^{f'({x}+{\Delta x})に対応} -\overbrace{{f({x}+{\Delta x})-f({x})\over {\Delta x}}}^{f'({x})に対応} \over {\Delta x} } \\[3mm] =&\lim_{{\Delta x}\to0} {\left( f({x}+{\Delta x}+{\Delta x})-f({x}+{\Delta x})\right) -\left( f({x}+{\Delta x})-f({x})\right) \over {\Delta x}{\Delta x} } \end{array} \end{equation}という式が出る。
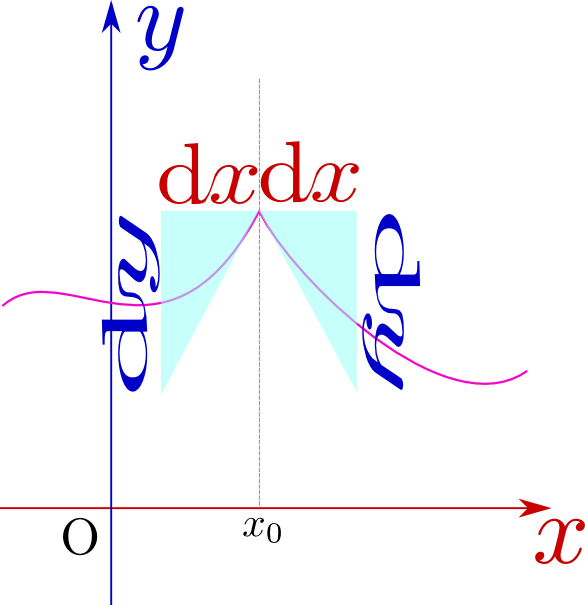
\begin{equation} \begin{array}{rll} f''({x}) =&\lim_{{\Delta x}\to0}{\left( f({x}+2{\Delta x})-f({x}+{\Delta x})\right) -\left( f({x}+{\Delta x})-f({x})\right) \over ({\Delta x})^2 } \\ =&\lim_{{\Delta x}\to0}{ f({x}+2{\Delta x})-2f({x}+{\Delta x}) +f({x}) \over ({\Delta x})^2 }\\ =&2\lim_{{\Delta x}\to0}{ { f({x}+2{\Delta x}) +f({x})\over 2} -f({x}+{\Delta x}) \over ({\Delta x})^2 } \end{array}\label{nikaibibunteigi} \end{equation}という計算になる。最後で2を前に出したのは、分子の${f({x}+2{\Delta x})+f({x})\over 2}-f({x}+{\Delta x})$に図形的意味があるからである。
その意味するところを説明しよう。下のグラフを見て欲しい。
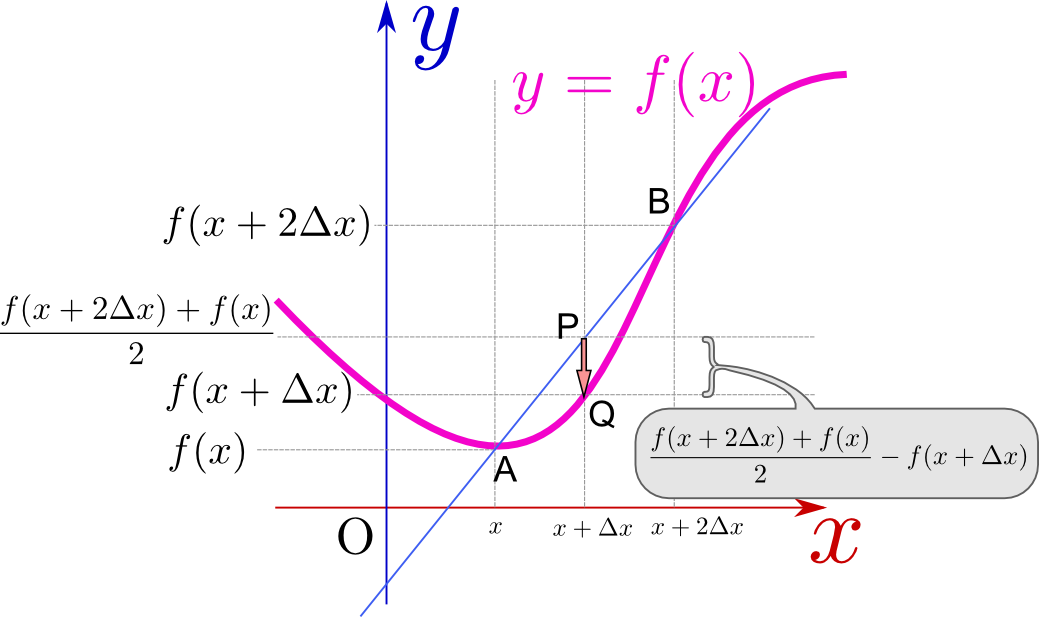
図の点Pは点A$({x},f({x}))$と点B$({x}+2{\Delta x},f({x}+2{\Delta x}))$の中点であり、その高さが${f({x}+2{\Delta x})+f({x})\over 2}$である。
一方$f({x}+{\Delta x})$は点Qの高さである。つまり、点Aと点Bの中点に比べて、点Qがどれだけ下がっているか、という量であり、これは「線の曲がり具合」を表現している。二階微分の値は「両隣の平均に比べて自分がどれだけ下がっているか」を示す量だとも言える。

それは上の図に示したように「上に凸か下に凸か」を表す量にもなっている。
自然において、二階微分が正なら増加し、二階微分が負なら減るという傾向を持つ現象がたくさんある(後で、微分方程式でこれを表現するとどうなるか、ということを示そう)。これはつまり、下に凸なら増加、上に凸なら減少であり、すなわち平坦に戻そうという傾向のある現象なのである(たとえば水面・温度分布・濃度分布などにこういう傾向がある)。
実のところ、自然法則の多くには二階微分までしか現れない。よって二階微分までをきっちりと理解していけば、自然法則のほとんどが理解できることになる。