自然科学のための数学2015年度第13講
微分積分学の基本定理
えらく大層な名前だが、実は単純なことで、一文で表すならば「積分の逆の演算が微分である」ということに過ぎない。
説明の前にもう一度確認しておくが、定積分$\int_a^b f({x})\mathrm dx$という量は、関数$f({x})$と、下限$a$と上限$b$のすべてに依存する。とりあえず関数$f({x})$の形と下限$b$は「変化しない」としておくと、定積分$\int_a^b f({x})\mathrm dx$は上限$b$の関数であると考えてもよい。つまり、
\begin{equation} F({b})=\int_a^{{b}}f({x})\mathrm dx \end{equation}のような関数$F({b})$を考える(実際にはこの量は$a$にもよるし、関数$f$の形にもよるので、$F_f(a,b)$とでも書くべきであろうが、ここでは$a$は変化しない定数だとして扱っているので略している)。この$F({b})$は後で定義する「原始関数」の一例である。
ここで、${b}$の変化による$F({b})$の変化の割合(つまり、微分)を考えると、
$F({b})=\int_a^{{b}} f({x})\mathrm dx$を${b}$で微分すると、${\mathrm d \over \mathrm db}\left(\int_a^{{b}} f({x})\mathrm dx\right)=f({b})$となり、元の関数(ただし、変数は${b}$)に戻る。
ということになる。
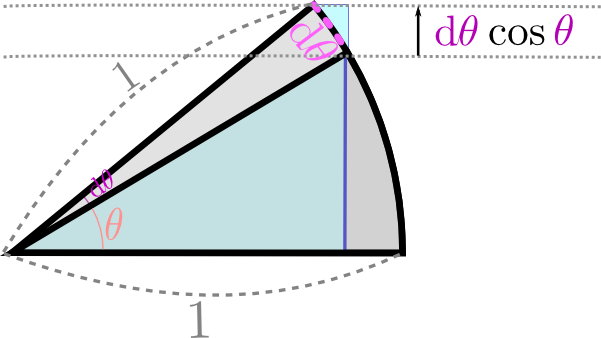
これが成り立つのは、ここまでやった定積分という計算の意味をわかっていればわかると思う。図でちゃんとその意味を確認しておこう。
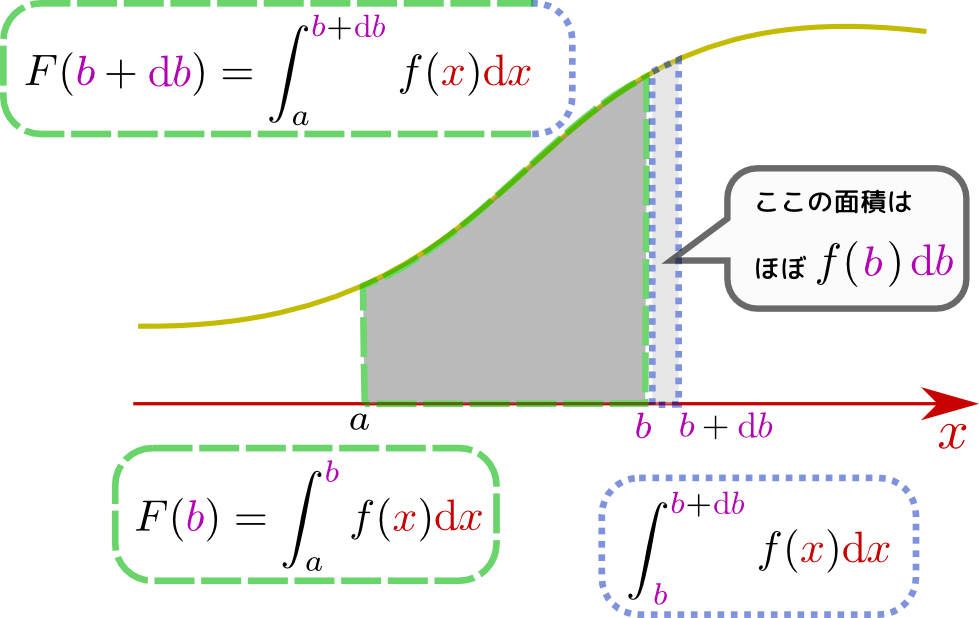
積分の上限${b}$をちょっと変化させる。積分の結果である面積は図に示した の分だけ増加することになる。この部分を例によって「幅$\mathrm db$、高さ$f({b})$の長方形」と考えると、$F({b})$の変化量は$f({b})\mathrm db$である(厳密には後に${\cal O}(\mathrm db^2)$がつく)。
の分だけ増加することになる。この部分を例によって「幅$\mathrm db$、高さ$f({b})$の長方形」と考えると、$F({b})$の変化量は$f({b})\mathrm db$である(厳密には後に${\cal O}(\mathrm db^2)$がつく)。
という式は、微分の式$f({x}+\mathrm dx)=f({x})+f'({x})\mathrm dx$と見比べれば、$F'({b})=f({b})$だということである。これで微積分学の基本定理が示せた。
別の言い方をすれば、微小な範囲の積分は
\begin{equation} \int_{{x}}^{{x}+{\small \mathrm dx}}f({y})\mathrm dy = f({x})\mathrm dx + {\cal O}(\mathrm dx^2) \end{equation}のように書くこともできるということである。
微分積分学の基本定理のありがたみは、どちらかというと面倒な計算である「積分」を「微分の逆」という形で計算できることであるこの講義ノートをここまで読んだ人は、もはや「微分は簡単」という気持ちになっているはずだ、と著者は思っているが、どうだろう?。たとえば我々は${\mathrm d \over \mathrm dx}\left({x}^\alpha\right)=\alpha {x}^{\alpha-1}$をすでに知っているので、前に区分求積でやった計算を経ずとも、
\begin{equation} {\mathrm d \over \mathrm dx}\left({x}^\alpha\right)=\alpha {x}^{\alpha-1}~~の逆として~~ \int_a^b \alpha{x}^{\alpha-1} \mathrm dx =b^\alpha - a^\alpha \end{equation}を得る。あるいは、$\alpha=\beta+1$として両辺を$\alpha$で割って、
\begin{equation} \int_a^b {x}^{\beta} \mathrm dx ={b^{\beta+1}\over \beta+1} - {a^{\beta+1}\over \beta+1}\label{teisekibunxalpha} \end{equation}という式を作ることができる。以下でもこれを使って計算しにくい積分を求めていく。
原始関数と不定積分
前節で使った記号$F({x})$は、「定積分の結果を上限の関数として表したもの」であったが、結局それは「微分したら積分する前の関数に戻るもの」でもあった。そこでより一般的に「原始関数(primitive function)」という関数$F({x})$を、
\begin{equation} 微分するとf({x})になる、すなわち f({x})={\mathrm d \over \mathrm dx}F({x})となる関数\label{gensikansuudef} \end{equation}で定義する(「原始」という言葉はもちろん「微分する前」ということ)。ただし、「定積分の結果を上限の関数として表したもの」は原始関数になるが、原始関数は常に「定積分の結果を上限の関数として表したもの」になるとは限らない。
ある原始関数が求められたとすると、それに任意の定数を足したものも、やはり原始関数である。
なぜならば、
\begin{equation} {\mathrm d \over \mathrm dx}\left(F({x})+C\right) ={\mathrm d \over \mathrm dx}F({x})+\underbrace{{\mathrm d \over \mathrm dx}C}_{0} =f({x}) \end{equation}となるから、$f({x})$の原始関数$F({x})$に定数を足した$F({x})+C$もやはり$f({x})$の原始関数たる条件(微分したら$f({x})$になる)を満たす。原始関数は一つに決まらないということになるが、原始関数の定義が必然的にそうなるようにできているのだから仕方がない。そもそも微分という演算が「定数を消してしまう」演算なので、「微分の逆」を考えた時に定数の分だけ決まらないのは当然である。
原始関数がわかれば、
\begin{equation} \int_{x_1}^{x_2}f({x})\mathrm dx = F(x_2)-F(x_1)=\bigl[F({x})\bigr]_{x_1}^{x_2}\label{teisekibungensi} \end{equation}のように「上限での原始関数の値$-$下限での原始関数の値」で計算できる。この量を(上の式の最後でも書いたように)$\bigl[F({x})\bigr]_{x_1}^{x_2}$という記号を使って書く。この式においても、原始関数$F({x})$の「定数$C$を足してもやはり原始関数である」という性質は変わらない。
\begin{equation} \int_{x_1}^{x_2}f({x})\mathrm dx = \bigl[F({x})+C\bigr]_{x_1}^{x_2} =F(x_2)+C-\left(F(x_1)+C\right)=F(x_2)-F(x_1)\label{kieruteisuu} \end{equation}となってこの式の結果に$C$は影響しないのである。
ここまでで考えた例では、${x}^\alpha$の原始関数が${{x}^\alpha\over \alpha+1}$である。上の式を見ると、
\begin{equation} \int_a^b {x}^{\beta} \mathrm dx =\left[{{x}^\alpha\over \alpha+1}\right]_a^b ={b^{\beta+1}\over \beta+1} - {a^{\beta+1}\over \beta+1} \end{equation}と書けることがわかるが、実際、
\begin{equation} {\mathrm d \over \mathrm dx}\left({x}^{\alpha+1}\right)=(\alpha+1){x}^{\alpha} \end{equation}となっている。
$c$を下限とした定積分$\int_c^{{x}}f({y})\mathrm dy$は原始関数の一つである。積分の例$\int_{x_1}^{x_2}{x}\mathrm dx$の場合、原始関数の一つは
\begin{equation} F({x})=\int_c^{{x}}{y}\mathrm dy=\left[{{y}^2\over 2}\right]_c^{{x}} ={{x}^2\over 2}-{c^2\over 2} \end{equation}ということになる(当たり前だが微分すると${x}$に戻る)。$c$がなんでもよいので、最後についている$-{c^2\over 2}$の分だけ、原始関数$F({x})$は不定性を持つ。これは上の$C$が任意であったことの反映である実は$-{c^2\over 2}$は常に0以下だが、$C$は正の数であってもよい(任意)から、$C$の方が範囲が広い。原始関数が必ずしも「定積分の結果の上限の関数」という形にならないと書いたのはこういう例があるからである。。
関数$f({x})$から原始関数$F({x})$を求めるという演算を「不定積分(indefinite integral)」と呼ぶ。不定積分のときは上限と下限を指定せずに、
\begin{equation} \int \mathrm dx f({x})= F({x})~~~または\int f({x})\mathrm dx=F({x}) \end{equation}のように書く。定積分の記号を流用して同じような形の式に書いているが、不定積分という操作は「関数$f({x})$から原始関数$F({x})$へ」という対応関係微分の「関数$f({x})$から導関数$f'({x})$へ」という対応関係の逆である。であり、一方の定積分は「関数$f({x})$と領域(下限〜上限)から、積分結果という一つの数へ」という対応関係である。
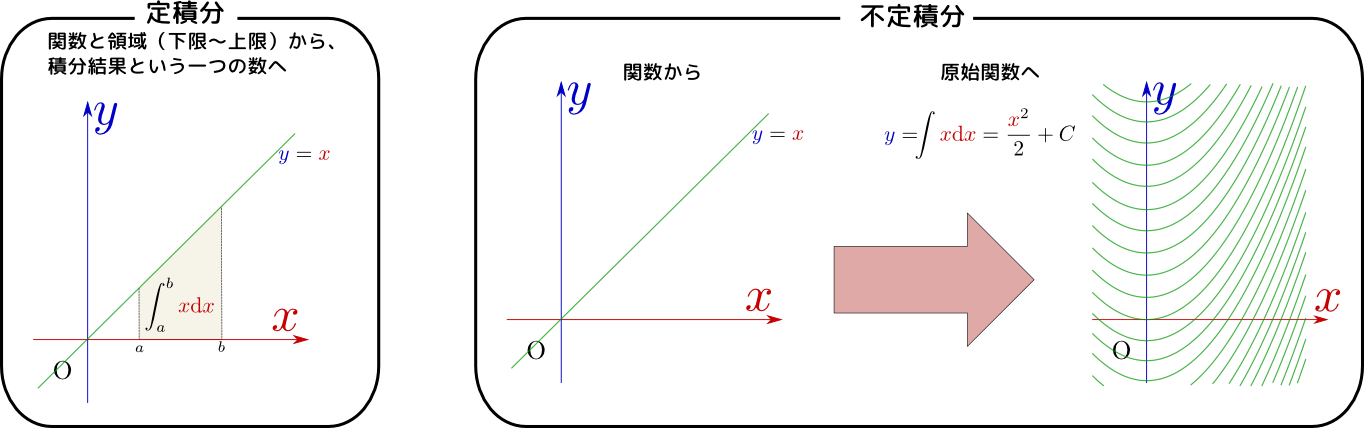
ちょうど、微分を「微分演算子${\mathrm d \over \mathrm dx}$を掛ける」ことで表現したように、不定積分という演算を「前から$\int$を、後ろから$\mathrm dx$を掛ける」$\int \mathrm dx f({x})$という書き方の時は「前から$\int\mathrm dx$を掛ける」でよい。という演算だとして表現していることになる。定積分の$\mathrm dx$は「微小な変化量」という意味が明確だったが、それに比べると不定積分の$\mathrm dx$はむしろ「積分という演算を表現する記号$\int \mathrm dx$」の一部であると言える。
不定積分は名前の通り、定数を付加できる分だけ決まらない。だから、
\begin{equation} \int {x}\mathrm dx = {{x}^2\over 2}+C \end{equation}のように「まだ決まってない定数(上の式の場合$C$)」をつけて結果を示す。これを「積分定数(constant of integration)」と呼ぶ(文字はよく$C$を使うがそうでなくてはいけないわけではない)。積分定数は不定積分の時は必要だが、定積分の時はどうせ消えてしまう運命にあるので、定積分に積分定数をつける必要はない(つけたければつけてもよいが)。