自然科学のための数学2015年度第14講
部分積分
微分のライプニッツ則
\begin{equation} {\mathrm d \over \mathrm dx}\left(f({x})g({x})\right) =\left({\mathrm d\over \mathrm dx}f({x})\right)g({x})+f({x}){\mathrm d\over \mathrm dx}g({x}) \end{equation}の逆を考えるのが部分積分である。公式を作ろう。まず上の式を不定積分し、少し項を入れ替える。
\begin{equation} \begin{array}{rll} \int {\mathrm d \over \mathrm dx}\left(f({x})g({x})\right)\mathrm dx =&\int \left({\mathrm d\over \mathrm dx}f({x})\right)g({x})\mathrm dx +\int f({x}){\mathrm d\over \mathrm dx}g({x})\mathrm dx\\ f({x})g({x}) =&{\underbrace{{\int \left({\mathrm d\over \mathrm dx}f({x})\right)g({x})\mathrm dx}}_{{←移項する}}} +{\int f({x}){\mathrm d\over \mathrm dx}g({x})\mathrm dx}\\ f({x})g({x})-\int\left( {\mathrm d\over \mathrm dx}f({x})\right)g({x})\mathrm dx =&\int f({x}){\mathrm d\over \mathrm dx}g({x})\mathrm dx \end{array} \end{equation}ここで、左右を取り替えて、
\begin{equation} \int f({x}){\mathrm d\over \mathrm dx}g({x})\mathrm dx =- \int \left( {\mathrm d\over \mathrm dx}f({x})\right)g({x})\mathrm dx +f({x})g({x})\label{pidint} \end{equation}
という公式ができる。なお、この式は結局はライプニッツ則を書き直しただけであり、独立に新しいものが出てきたわけではない。ここで行っている計算は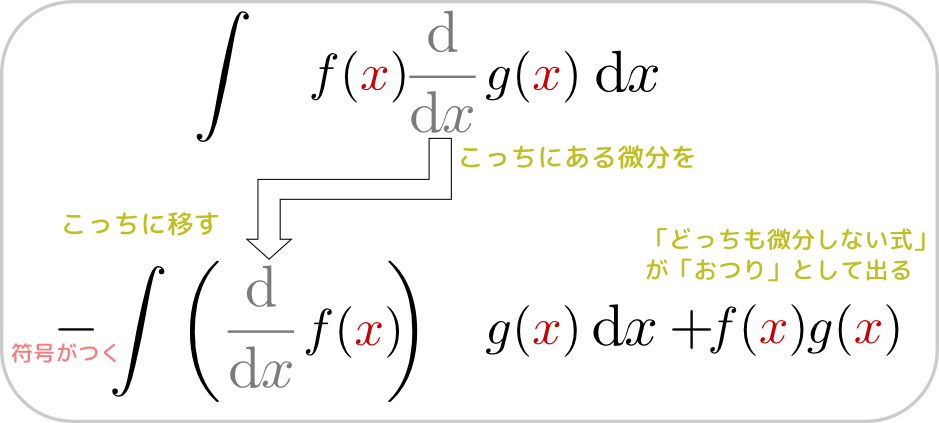 という操作だと考えてもよい。
という操作だと考えてもよい。
特に、「${\mathrm d\over \mathrm dx}g({x})$が積分しやすい($g({x})$を求めやすい)」かつ「$f({x})$が微分すると簡単になる」場合に部分積分という操作は有効である。
例として、$\int {x} \cos {x} \mathrm dx$をあげよう。この場合、${\mathrm d g\over \mathrm dx}({x})=\cos{x},f({x})={x}$という代入を行っていけば、
\begin{equation} \int \underbrace{{x}}_{f({x})}\underbrace{\cos {x}}_{g'({x})} \mathrm dx = - \int \underbrace{1}_{f'({x})}\underbrace{\sin {x}}_{g({x})} \mathrm dx +\underbrace{{x}}_{f({x})}\underbrace{\sin {x}}_{g({x})} =\underbrace{\cos {x}+C}_{\tiny -\int \sin {x}\mathrm dx} +{x}\sin {x} \end{equation}のようにして積分ができる。この式の2行目で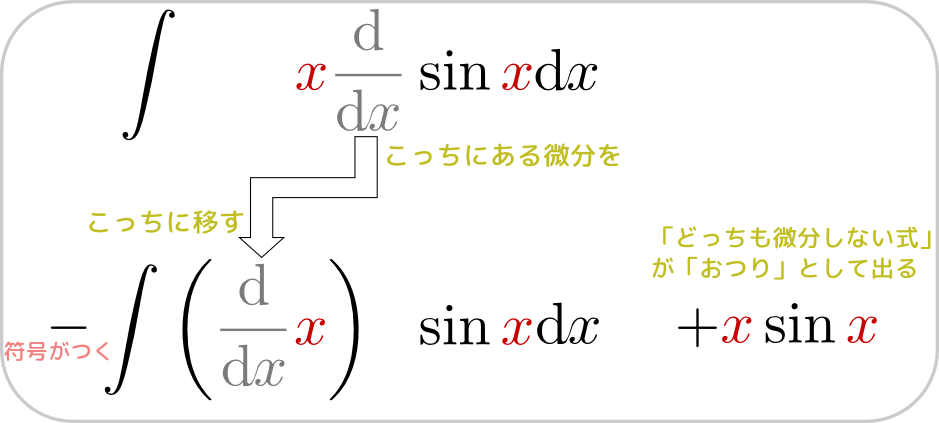 という操作を行っているわけである。
という操作を行っているわけである。
定積分の場合も同様に計算ができて、
となる。最後の部分は$\left[f({x})g({x})\right]_a^b=f(b)g(b)-f(a)g(a)$となって、積分の「表面」である${x}=a$と${x}=b$での値だけになるので、「表面項」と呼ばれる。
置換積分
${x}$を独立変数としたある積分$\int f({x})\mathrm d x$という積分を考える。ここで、${x}=g({t})$という別の変数へと独立変数を変えた時に、積分という量がどう変わるかを考えてみる。まず、$f({x})$という関数は$f(g({t}))$という${t}$の関数へと変えなくてはいけない。と同時に、積分要素も変わることになるが、この時、$\mathrm d x={\mathrm d x\over\mathrm dt}\mathrm dt$という関係を使って変換する。具体的にはこうなる。
置換積分の公式
\begin{equation} \int f({x})\mathrm d x = \int f(x({t})){\mathrm d x\over \mathrm dt}\mathrm dt \end{equation}この式は合成関数の微分則(chain rule)の逆をやっていると思えばよい。$f({x})$の原始関数を$F({x})$とする。ところでこの${x}$は${t}$の関数なので、$x({t})$と書くことにする($F(x({t}))$)。この式を$t$で微分すると、
\begin{equation} {\mathrm d \over \mathrm d t }\left(F(x({t}))\right) =\underbrace{\left( {\mathrm d \over \mathrm d x }F({x})\bigr|_{{x}=x({t})}\right)}_{f({x})}\left( {\mathrm d \over \mathrm d t}x({t}) \right) \end{equation}であるが、これをもう一回${t}$で不定積分すれば、
\begin{equation} F(x({t})) =\int f({x}) \left( {\mathrm d \over \mathrm d t}x({t}) \right)\mathrm dt \end{equation}となり、公式が出てくることになる。
いい。$\mathrm d x$ や$\mathrm dt$がどのような意味を持つかを考えよう。${\mathrm d x \over \mathrm dt}$とは微小変化$\mathrm d x $と$\mathrm dt $の比と考えることができるのだから、まさにこの式が成り立つ(ただし、積分変数が変わったということは定積分の積分区間も一緒に変わることには注意)。積分の式$\int f({x})\mathrm d x$というのは単なる記号ではなく、$f({x})$に微小変化$\mathrm d x$ を掛けて``足し算''するという意味を持っている。置換積分はその足し算のやり方を変えている。次の節で詳しく説明しよう。
たとえば
\begin{equation} \int {x}\sin {x}^2\mathrm d x \end{equation}において、${x}^2={t}$とおくと、$2{x}\mathrm d x =\mathrm dt$となるから、
\begin{equation} \int {x}\sin {x}^2\mathrm d x={1\over 2} \int \sin {t}\mathrm dt=-{1\over 2}\cos {t}+C=-{1\over 2}\cos {x}^2+C \end{equation}と書きなおしてよい。
ここで、被積分関数の中に${x}$があったら計算できたが、もしなかったらどうなるだろう?---$\int \sin {x}^2 \mathrm d x$または$\int \cos {x}^2 \mathrm d x$は計算できるだろうか??---試してみるとよいが、置換積分や部分積分などのテクニックを駆使しても、この積分は遂行できない。
このような積分は「フレネル(Fresnel)積分」と呼ばれるのだが、知られている関数の形で積分結果を表現することはできない。まず$\sin{x}^2$または$\cos {x}^2$をテイラー展開して${x}^n$の形にしてから積分するという方法で解を求めるしかない。置換積分でやっていることの図解
まず、置換積分を使うとできる積分の例として、$\int_0^1 \sqrt{1-{x}^2}\mathrm d x = {\pi\over 4}$という計算を取り上げる。
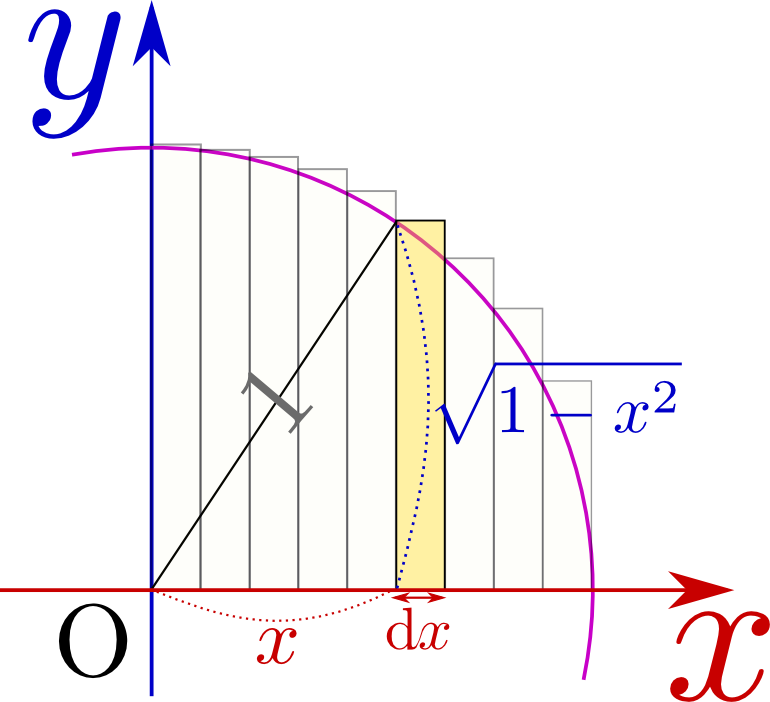
この計算がどのような意味を持つかを上のグラフに示した。これは高さ${\sqrt{1-{x}^2}}$で横幅が\mathrm d x である微小な長方形を${x}=0$から${x}=1$まで変化させながら足していった結果である。グラフを見ればわかるように、それは4分の1円の面積である。そう考えれば答えが${\pi\over 4}$なのは当然と言える。ではこれをどうやって計算するかであるが、置換積分という計算テクニックとしては、以下のように行う。
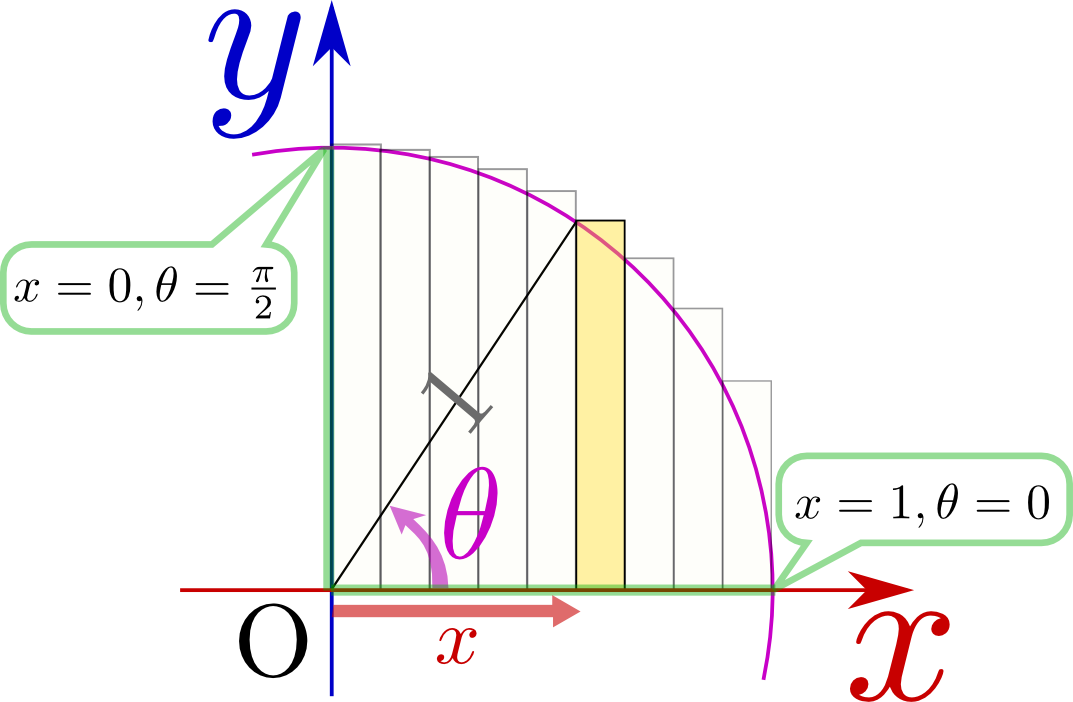
まず、$x=\cos {\theta}$と置いてみる。このような「置き換え」の方法は多くの場合、試行錯誤「$\sqrt{1-x^2}$は0から1の範囲で変化する関数だから、$\cos$とかどうかな?」のようにいろいろやってみる。の末に得られる。しかし、ここで考えているように、グラフを描いて図形的に考えてみると、どういう変換を行っているのかが見えてきて、計算の見通しがよくなることもある。実際、${\theta}$には右に描いたような意味がちゃんとある。${x}=\cos{\theta}$なのだから、$\sqrt{1-{x}^2}=\sin{\theta}$である$\cos ^2{\theta}+\sin^2{\theta}=1$という式で考えると$\sqrt{1-{x}^2}=\pm\sin {\theta}$となるが、図でわかるように${\theta}$は0から$\pi$までだから、$\sin{\theta}$の前に符号は必要ない。が、それは図に示した長方形の高さである。
$x=\cos{\theta}$を微分して、$\mathrm d x = -\sin{\theta} \mathrm d\theta $である。すると、$\sqrt{1-{x}^2}\mathrm d x = -\sin^2{\theta} \mathrm d\theta $と置換される。積分範囲は$x=0$のとき${\theta}={\pi\over 2}$、$x=1$のとき${\theta}=0$としよう。つまり、積分変数を$x\to {\theta}$と変える時に$\int_0^1$は$\int_{\pi\over 2}^0=-\int_0^{\pi\over 2}$と置き換わる。計算すべきは$\int_0^{\pi\over 2}\sin^2{\theta} \mathrm d\theta $である。$\sin^2{\theta}={1-\cos 2{\theta}\over 2}$と置き換えると、
\begin{equation} \int_0^{\pi\over 2}{1-\cos 2{\theta}\over 2}\mathrm d\theta = \left[ {{\theta}-{1\over 2}\sin2{\theta}\over 2} \right]^{\pi\over 2}_0 ={{\pi\over 2}-{1\over 2}\sin \pi\over 2}-{0-{1\over 2}\sin 0\over 2} ={\pi\over 4} \end{equation}と積分できる。
なお、この積分は上のように真面目に計算してもよいが、
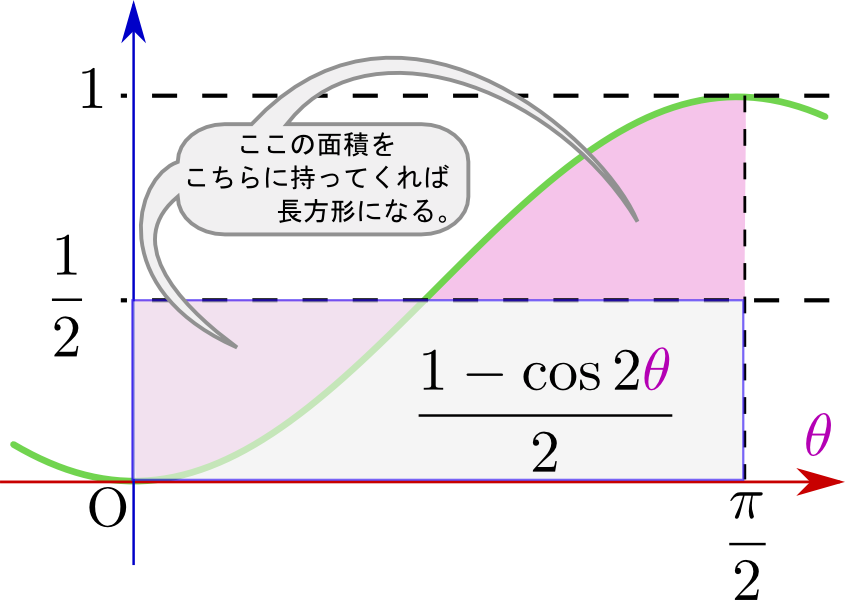
のようにグラフを描いて考えると、被積分関数のうち${-\cos2\theta\over2}$の部分は「谷→山」へと振動する関数で、この部分は結果に寄与しないだろう(図で塗りつぶした部分がちょうど消える)、と考えることで「横幅${\pi\over 2}$で高さが${1\over 2}$の長方形の面積だと同じだと考えて、${\pi\over 4}$という答えを出してもよい。
さて、以上の手順を図解しておこう。
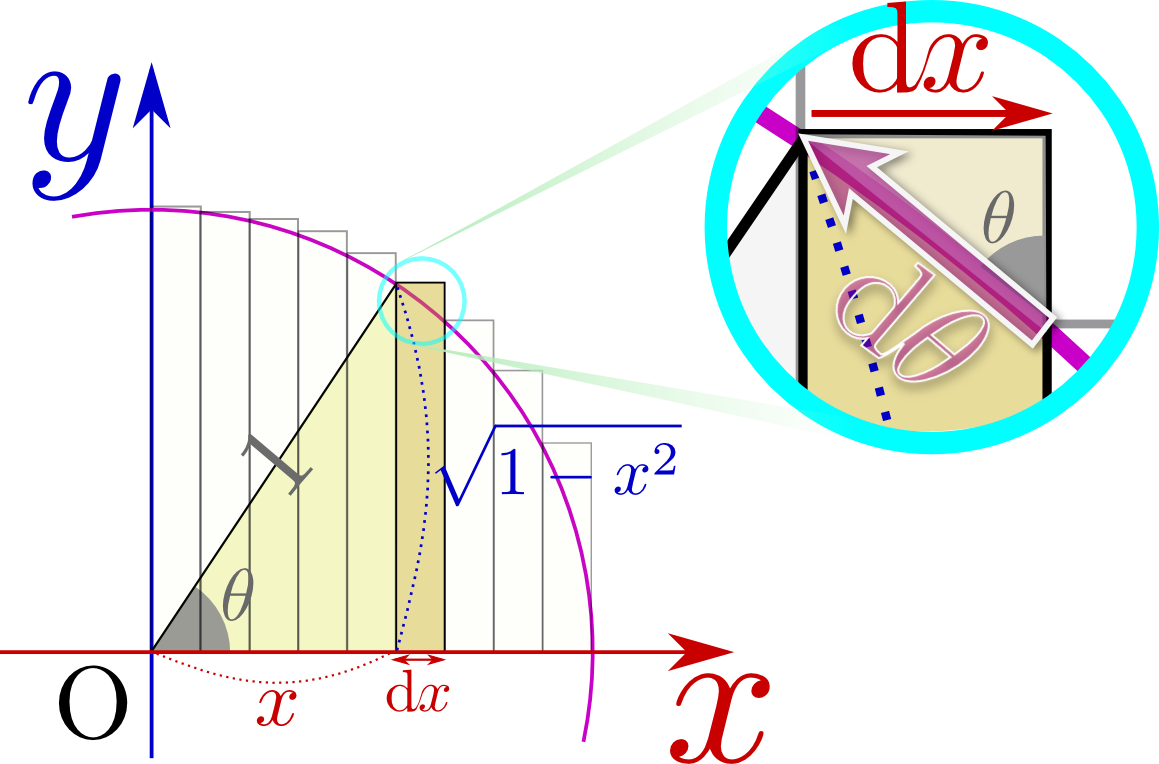
${\sqrt{1-{x}^2}}\mathrm d x$というのは、右の図の長方形の面積であり、積分とはこの長方形を足していくということである。${x}=\cos{\theta}$と置くということは、図のように角度${\theta}$を設定しているということであり、$\mathrm d\theta$という量は、図の弧の部分の長さでもある(単位円であることに注意)。
この部分の拡大図を見ると、(上では${x}=\cos{\theta}$を微分して出した)$\mathrm d x=-\sin{\theta} \mathrm d\theta $が図の関係として表現されていることがわかる。特に、$\mathrm d x $と$\mathrm d\theta$の符号が逆(${x}$が増えれば${\theta}$が減る)であることに注目しよう。
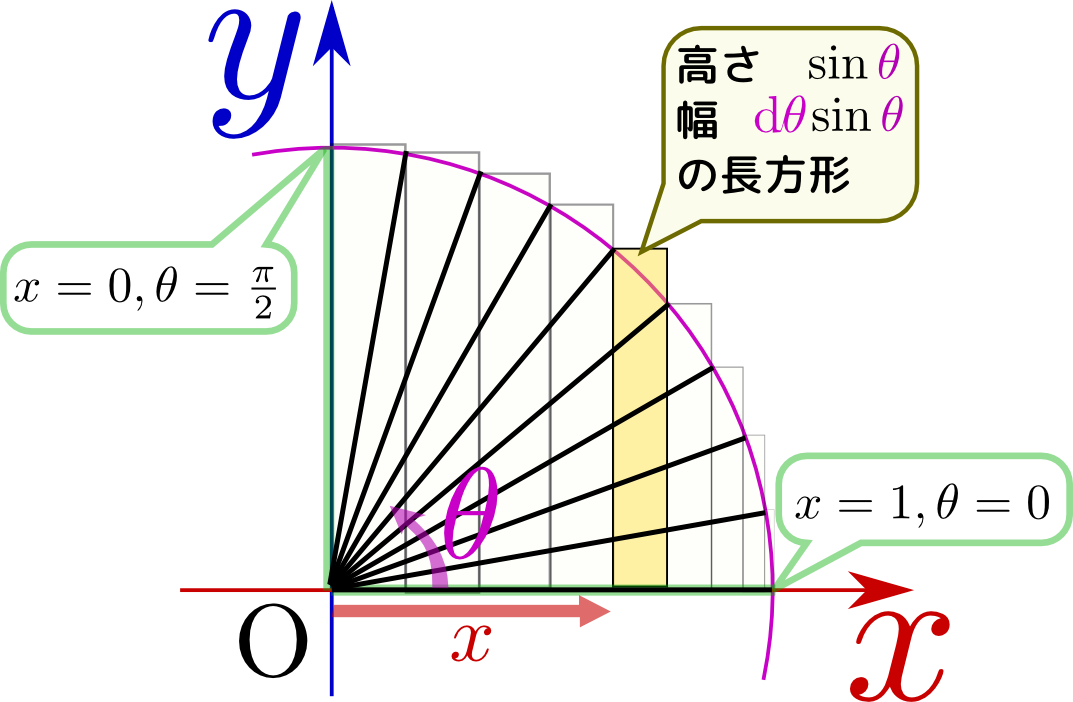
${\theta}$を変化させていった時のそれぞれの微小長方形を描いたのが右の図である。「高さ$\sin{\theta}$、幅$\mathrm d\theta \sin{\theta}$の長方形」を足していくという計算になっている(${x}$の積分の時は「高さ$\sqrt{1-{x}^2}$で幅$\mathrm d x$」だった)。これが$\sqrt{1-{x}^2}\mathrm d x=-\sin^2{\theta}\mathrm d\theta $という置き換えの意味なのである(マイナス符号の意味は先で説明した通り)。
次に、$\int_0^\infty{1\over 1+{x}^2}\mathrm d x$という積分を考えよう。この積分は、$x=\tan{\theta}$と置き換えることにより、
\begin{equation} \int_0^{\pi\over 2}{1\over 1+\tan^2{\theta}}\underbrace{{\mathrm d\theta \over \cos ^2{\theta}}}_{\mathrm d x} = \int_0^{\pi\over 2}\mathrm d\theta ={\pi\over 2} \end{equation}のように計算できる($1+\tan \theta^2={1\over \cos^2\theta}$に注意)。積分区間は「${x}=0$から${x}=\infty$」が「${\theta}=0$から${\theta}={\pi\over 2}$」と変わる。
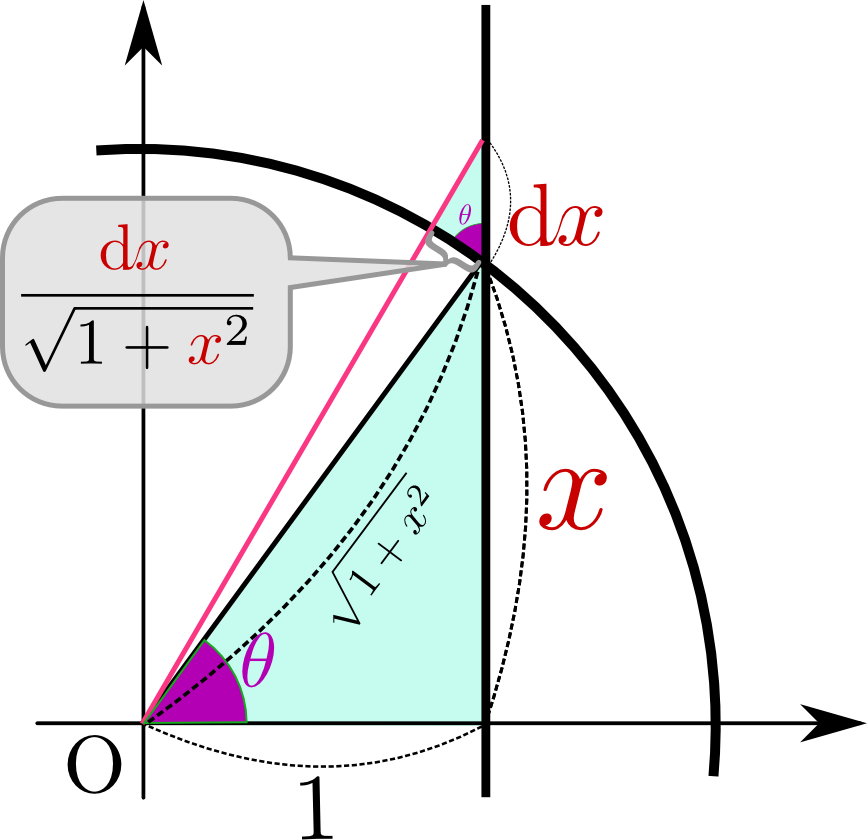
図を見て${x}$を0から$\infty$まで動かしたら${\theta}$がどう変化するかをみればよればこれがわかる。
ではどうして${1\over 1+{x}^2}\mathrm d x$という「微小部分」の和が角度積分になるのだろうか。

上の図に、底辺1、高さ${x}$の直角三角形の高さを$\mathrm d x$だけ大きくしたときの変化を示した。この時、図に示した角度${\theta}$の微小変化$\mathrm d\theta$を考えると、${1\over 1+{x}^2}\mathrm d x$になるのである。この角度を知るにはどうすればよいかというと、図に示したように扇型の弧の部分の長さ${\mathrm d x \over \sqrt{1+{x}^2}}$である」ことがわかる。「半径$\sqrt{1+{x}^2}$の円の一部である扇型の弧の長さが${\mathrm d x \over \sqrt{1+{x}^2}}$ということは、角度は${\mathrm d x \over \sqrt{1+{x}^2}}\div\sqrt{1+{x}^2}={\mathrm d x \over {1+{x}^2}}$である」と考えればこの置換が何をやっているのかがわかる。
問題により、そして(思考方法は人それぞれなので)個人により、「どう考えれば理解しやすいか」は違う。では「式で計算できればそれでよい」(または「図解できればそれでよい」)かというと、次に現れる問題があなたにとってどちらで理解しやすいかはわからないわけだから、いろんな方法で理解するということを(少なくとも``数学修行''をしている間は)心がけておいた方がいいだろう。立ち向かう相手(自然科学)は強大なのだから持っている武器は多い方がよい。
ときどき「たくさん教えられてもわかんなくなるから、教える方法は一つにしてください」という人がいるのだが、一つしか武器がない状態では太刀打ちできない強敵に出会う時のために、修行はしておこう。
期末テストは8月6日にあります。
試験では、A4一枚の「自作カンニングペーパー」持込可です。自分が忘れそうな公式や問題の解き方などを書いてきてください。それ以外(教科書など)は持ち込み不可です。
「自作」に限りますが、他の人と共同で制作するのは構いません。