青字は受講者からの声、赤字は前野よりの返答です。
微分評定式の使い途がとても凄いと思った。
まだまだいろいろありますよ。
単位が取れるよう頑張ります。
頑張りましょう。単位の為というよりは、数学を理解し使えるようになるために。
微分方程式の例が楽しかった。帰ったら教科書に書いてある他の例を見て楽しみます。
読んで、計算してみてください。
良い授業だった。
どうも。
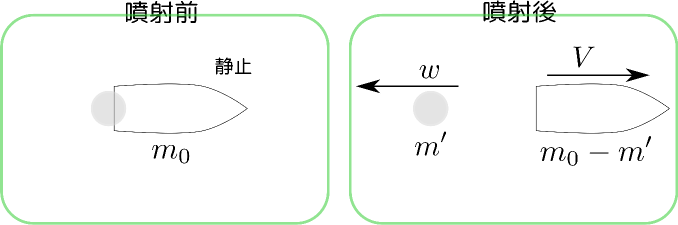
めっちゃわかりやすかったです! 物理学演習でわからなかったところがわかりました! 運動量保存の高校と違うのにびっくりしました。
高校の範囲では微分方程式にできないので「噴射は一度に行われた」ということにして計算してます。
微分方程式は誤差はあれど全ての現象を式、グラフにすることができる?
いい質問です。ほとんどの場合はできます。ただ、世の中には微分ができない現象もある(たとえば水が水蒸気になるとき、急激に体積が増える、など)もあるので、「全て」とはいきません。
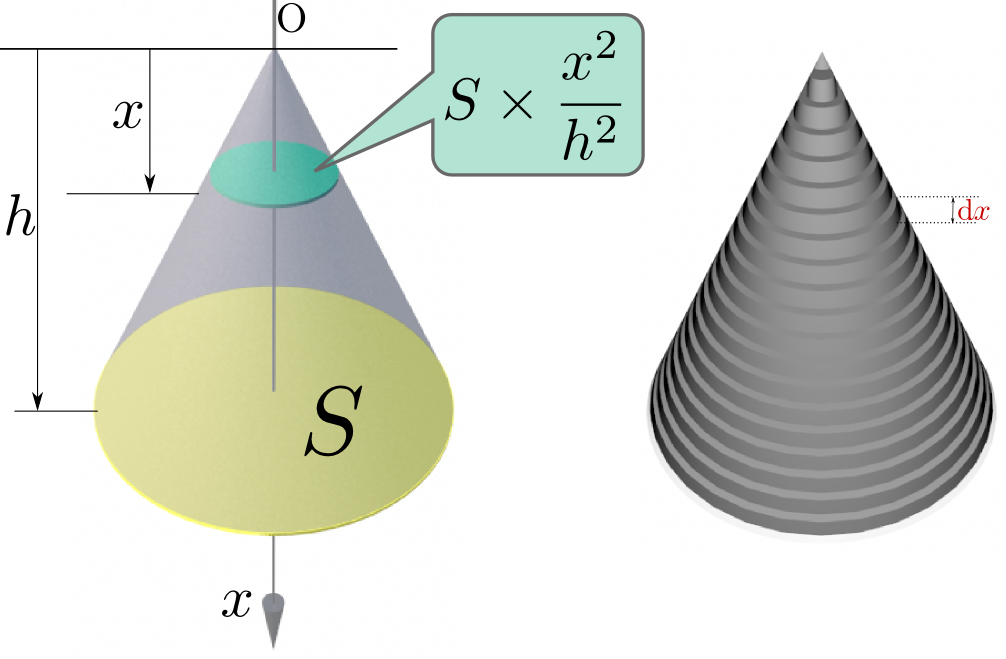
円錐や球の体積の公式は、積分を使って導き出されていることを初めて知りました。
実はそうです(というか、それ以外では求められない)。
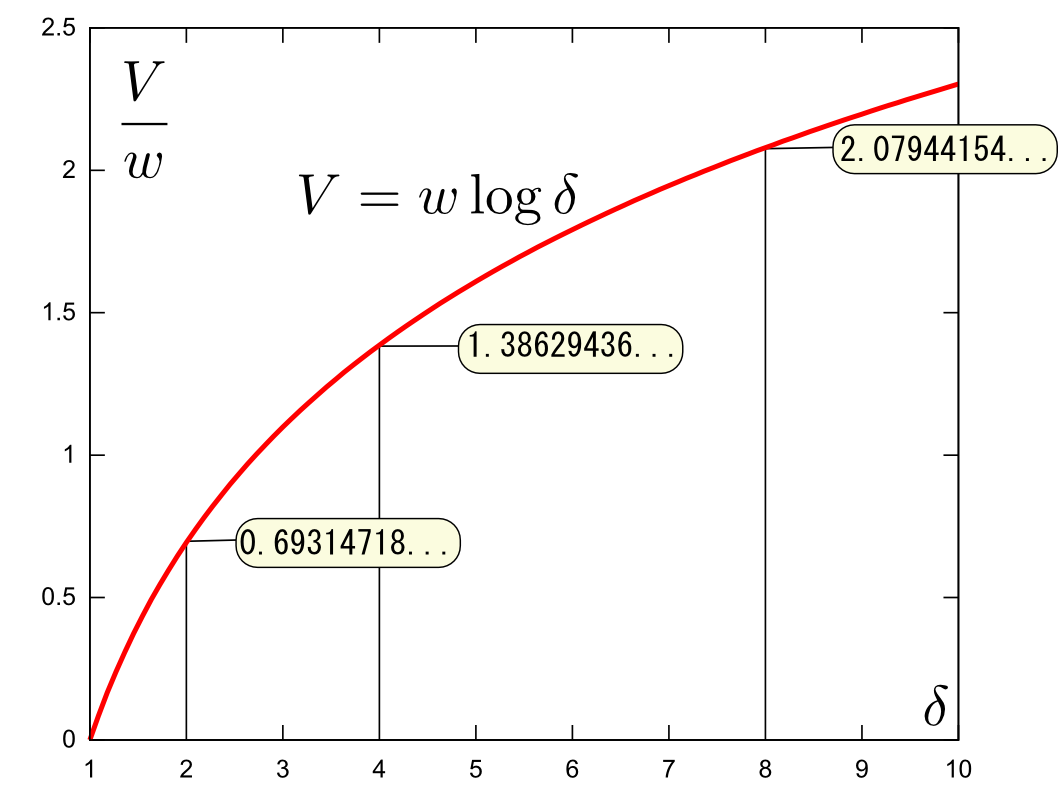
ロケットの燃料タンクがあんなに大きい理由が数式からわかった。戦争の兵力もわかったので微分方程式の威力がわかった。
logという関数があまり大きくならない関数なのでああなります。
微分方程式がかなり万能だということがわかった。おそらく今後ずっと使っていくと思うので慣れていきたい。
今後も使う機会は多いでしょう。
微分方程式まじ楽しかったです! 微分と積分を両方使っているのが面白いし、色々な自然現象が表現できるのも楽しかったです。ロケットの燃料が灯油というのは地味に知らなかったです。
立てたり解いたりすると微分方程式は楽しいです。
あらゆる自然現象を微積分で説明できるというのはすごいなと思いました。戦争まで計算できるとは思いませんでした。来週のテストはがんばりたいです。
「あらゆる」は言い過ぎですが、かなり説明できます。
最後のロケットの燃料や戦争も微分方程式で出せて面白かったです。先生の授業楽しかったです! ありがとうございました。
こちらこそ、ありがとうございました。
ロケットの打ち上げ、兵力までも微分方程式で出せることにびっくりした! 流行の方程式も気になる…。
流行については、テキスト読んでおいてください。
自然現象だけでなく戦争まで微分方程式が使えるとわかって非常に便利だと思った。
とても便利です。
積分の面白さ、微分方程式を使って解く面白さを知ることができた。活用できるようにしていきたいと思った。
使えるようになると楽しいですよ。
微分方程式を極めたいです。
極めましょう、今後のためにも。
微分方程式について学んだが、次はもっと複雑な問題にも挑戦したい。
後期のIIでもいろいろやりましょう。
なぜ円錐の体積を求める式が$V={1\over3}Sh$なのかわかった。また、自然現象や戦争なども微分で考えられるという話が面白かった。
少しずつ変化していくような量は、だいたい微分方程式でなんとかなります。
微分方程式凄い。
凄いです。
微分方程式を勉強してみて微分する意味や積分する意味がよくわかった。もっと勉強してみたくなった。
もちろん、勉強してください。
来週のテストに向けて今までの復習がんばる。
はい、がんばりましょう。
微分方程式は様々なものに利用されていることがわかった。戦争すらも計算が組まれているのに驚いた。
数学の使い途はかなり広いですよ。
面白い内容でした。
それはよかった。
戦争の兵力についても微分方程式で解けるのはとてもおもしろかったです。
いろいろ使えて面白いでしょ。
いろんな現象を微分方程式で解けるのがすごく楽しかった。
自分でもやってみてください。
微分方程式がいろいろな現象の予測を可能にすることを知り、もっと知りたいと思いました。
後期のIIでじっくりやります。
円錐や球の体積の公式の意味がわかった。試験頑張りたい。
頑張りましょう。
微分方程式はすばらしいです。
立て方、解き方を身につけてください。
微分方程式を理解できた。
それはよかった。
微分方程式の具体例が計算がわかったんですが、物理的な意味がよくわからなかったです。
う〜ん、物理的意味が式とつながることが大事なんですが。
テスト頑張ります。
はい、頑張って。
面積・体積などの計算について学んだ。
練習しておきましょう。
ロケットの話は高校物理で問題としてよく出ていたが、このようなことに全く気づいてなかった。今回このことを言われると納得すると、とても興味深いと思った。
高校の時にやった問題、よく見ると「噴射は一度で」とか書いてありませんでしたか?
勉強がんばります。
がんばってください。
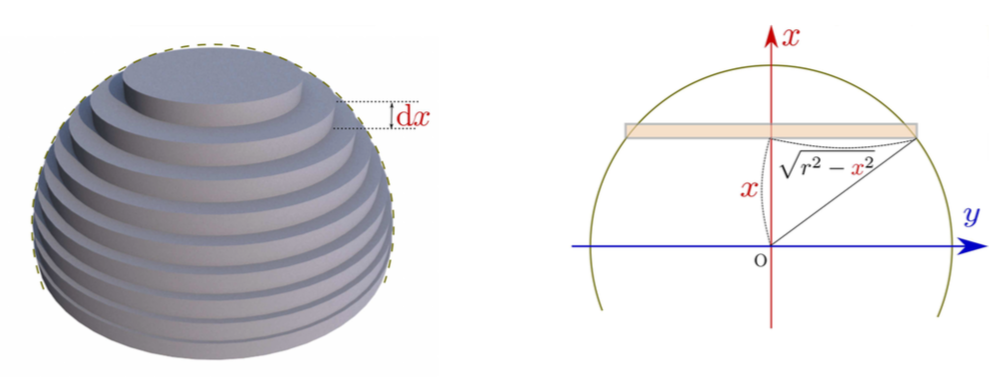
球を表面積で切る方法は目から鱗、でした。流行りを微分方程式で説明できるなんて、すごいぞ微分方程式!
微分方程式はほんとに役に立ちます。
この授業を受けて、これまでの私の数学や物理の考え方が大きく変わったと思います。イメージをすることができるようになり、さらに様々な公式を連動させて問題を解いたり考えたりできるようになりました。テストちゃんと単位を取れるように頑張ります。
授業が役に立ったようでよかったです。それは単位よりも大事なことです。
最後の兵力の奴はおもしろかったです。もっといろんな微分をしてみたいです。
やりましょうやりましょう。
一般的な事象にあてはめて、自分で微分方程式を解いてみることにもチャレンジしていこうと思いました。
チャレンジしてください。自分でやってみるのが上達への道。
微分方程式の有用性はとてもおもしろい。
とっても役に立ちます。
放射性の消えるのを計算するのを$\mathrm dN=-\alpha N\mathrm dt\to N(t)=N_0\mathrm e^{-\alpha t}$で求めきれることに感動した。
微小な時間での現象から、未来が見える、というのが楽しいところです。
微分方程式がとてもおもしろかったです。色々なもので使えるというのは知っていましたが戦争などにも使われているのは知らなかったのでおもしろかったです。
少しずつ法則にしたがって変化するようなものなら、何にでも使えます。
計算例を見るととても微分方程式は便利なものだなと思いました。マスターできるよう勉強したいと思います。
はい、とても便利です。是非マスターしてください。
私はあんまり戦争をしたことがないので、そんな微分方程式の活用性があるとは知らなかった。
まぁ、普通は戦争したことがないと思います。
ロケットの話で運動量の保存は正しいが、微笑時間でみてみるとじょじょに機体の速度が速くなり、じょじょに質量が減る。よってロケットから見た燃料噴射の速さがじょじょに増えると、機体の速さ$V$もじょじょに増える。
ロケットから見た燃料噴射の速さ$w$は一定です。それを外から見ると遅くなるように見える。
ロケットの到達速度と兵力自乗の法則がとてもおもしろかったです。
微分方程式を自分で立ててみてください。