青字は受講者からの声、赤字は前野よりの返答です。
「多項式関数なんて中学校でほぼやり尽くしただろ?」と思いましたが、パラメータから平行移動を考えるのは面白かったです。平行移動=平方完成ということでしか考えてなかったので、また数学が楽しくなった気がします。
やり尽くしたように思えても、係数と関数の形の関係について、こういう「勘」が働くようになっていないと関数を使う立場としてはまだまだ、関数への親しみ方が足りない。
ジェスチャーが豊富で授業がわかりやすかった。ただ早く、大学で扱えるような微積分を学習したい。
今やっていることも「微積」の心をつかむために必要です。
高校の時に当たり前に使っていたことが改めて理解できた。先生のジェスチャーがおもしろかったです。
身体も使って(^_^;)、数学を理解していきましょう。
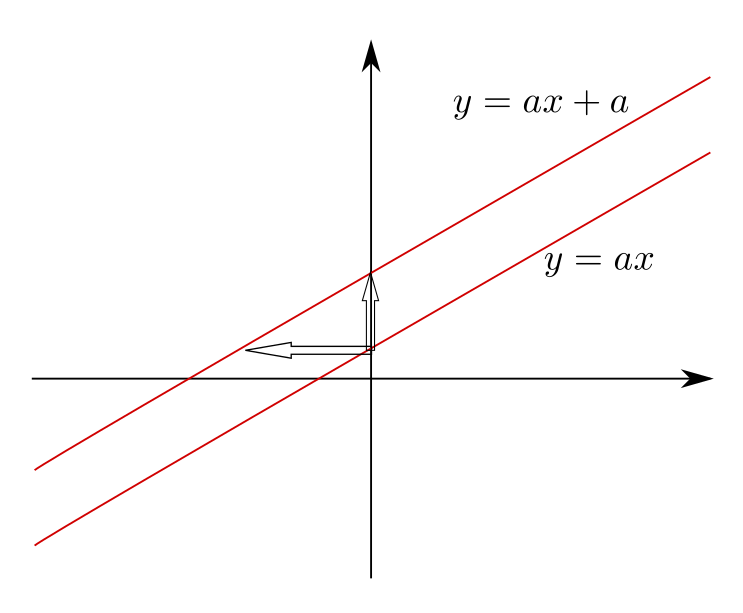
1次関数ではx軸方向に平行移動するのも、y軸方向に平行移動するのも同じになるのは知らなかった。実際にグラフを見るのはとても印象に残るので面白かった。
1次関数というのは、ある意味「簡単すぎる関数」なのです。
初めて受講したのでタブレットを使ってする授業とてもわかりやすかったです。関数のこともよくわかりました。
動く図でイメージをつくっていきましょう。
各項が変化するとグラフでどの部分が変わるのかがよくわかりました。
式とグラフを結びつけて理解することが大事です。
関数を決めるパラメータなどについては今まで考えていなかったので面白かったです。
いろんな関数の形がどう決まるのか、式と連結して理解しましょう。
関数のx=0付近の影響の大きさの感覚がなんとなく分かったと思う。
この「付近の影響」という物の見方、大事です。
係数は形を決めるものと位置を決めるものに分けられていると知ったので驚きました。
それぞれの係数にそれぞれの役割があります。
高次の関数でも、x=0付近ではxの係数が傾きを表すという見方をしたことはなかったので、知れてよかったです。
この「付近でこうなる」という考え方が、微分につながっていきます。
グラフの形を係数で変えるんだなぁって思いました。
関数に含まれるパラメータは、それぞれにグラフの形の情報を担ってます。
関数にはパラメータが存在し、そのうち平行移動のパラメータがあるということが分かった。
関数はいろんなものがありますから、それぞれにパラメータを持ってます。
多項式関数の平行移動の仕組みがよくわかった。
平行移動の概念も、大事です。
多項式のそれぞの項が持つ性質や、関数の形を決めるパラメータ、平行移動するパラメータの話がとてもわかりやすく、楽しかったです。
関数の「形」を何が決めるのか、という概念を持っておきましょう。y
1次の係数が原点付近では傾きを表していることがわかり面白いなと思った。また、グラフの形を決めるパラメータと平行移動を表すパラメータがあることが分かり、1次関数においては区別がつかないためパラメータが一つになるなど、初めて聞く話がたくさんありとても為になった。
この「傾き」がどう決まるかというのが、微分を勉強するときとっても大事です。
多項式関数と平行移動をならった!! 高校の時も習ったけど、こんなに細かく習ってなかったら、あんがいたのしかった。
高校のときも、きっといろいろ習ったはずですよ。
高校の授業では一つの決まりとして習っていたことを、ではそれがどうしてこうなるのかという視点からみていくと、これまで見えてこなかったことがわかるようになっていくことは、とても楽しいです。
「なぜ」という視点は常に持ちましょう。自然科学の為です。
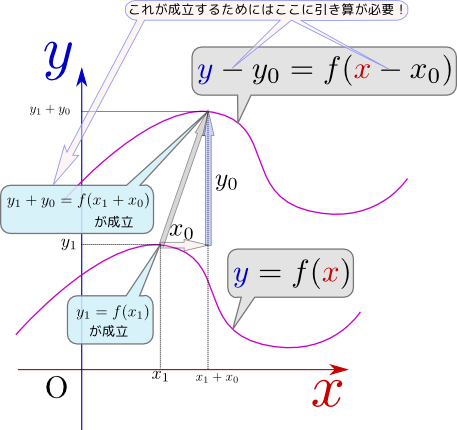
平行移動の際、プラスではなくマイナスなのはなんでだろうと気にしたことがありませんでした。理解できました。
数式のいろんなところ、是非気にして、答えを見つけてみてください。
xが0付近が大切な話が面白かったです。x家の近所付き合いを想像しました。肩、お大事に。
近所(数学的には「近傍」という言葉をよく使う)をまず考える、これ大事。
1次関数の平行移動でx方向とy方向の平行移動の本質は変わらないのはなるほどと思った。
1次関数は特に簡単な関数なので、そういうことになります。
大体理解できた。
それはよかった。
今日はついていくことができた。この調子でがんばりたい。
がんばりましょう。
多項式関数、平行移動について。パラメータの存在の発見。
いろいろ話しましたが、納得できましたか?
平行移動のとき、自分も$x_0$を足すのか引くのか迷ったが、図でみるとよくわかった。これからは迷ったときは図を描いてみるようにしたい。
図を書くのは大事です。どんどん書きましょう。
しっかりと関数の法則を復習できてよかった。
それはよかった。
基礎のところだから余裕だろうと思っていたが案外わからなくて少し驚いた。またついていけるように復習したい。
基礎ではありますが、だからこそしっかり理解しておかないとね。
原点付近を注目するのが大事だと分かった。平行移動をきちんと理解できるようにしたい。
はい、どちらも大事です。
家でしっかり復習して、今日の内容は特に定着させたい。
やりましょう。
2次関数のx=0付近ではグラフはほぼ直線とみなせて、1次の項の係数がその傾きを表すことがわかった。
それが後で出てくる「微分」の考え方の第一歩です。
よく使っている関数も、深く考えたりグラフをじっくり見てみると、面白い発見があった。
他の関数についても、深く考えて発見していきましょう。
平衡移動のところを最初間違えていたので、次は間違えないようにしっかり復習したいです。
平行移動で何が起こるか、その意味を考えれば、間違えないはず。
段々と先生の威圧感を押し返せるようになりたいと思った。あと、この授業にはちょっとした衝撃を受ける。
まぁ、威圧感など押し返してください。
自分でグラフの性質がみつけられないものもありましたが、説明を聞いてすごく納得することができました。
いろいろとグラフを見ながら、考えてみてください。
多項式の大事な項とかがわかった。教科書の変数に漢字を使ったりすることに賛同します。
大事なところを理解しておきましょう。
多項式関数$y=ax+b,y=ax^2+bx+c,y=ax^3+bx^2+cx+d$。イメージ感覚に問う授業だった。原点付近においてのグラフの概形を重視した。
イメージと、「原点付近を見る」という視点、とても大事です。
今まで、意味を考えずに覚えこむことが多かったですが、そのまま次へ次へ難しいところにいくとつまってしまうので、よく復習しておきます。
やはり意味を知らないと勉強する意味も勉強しがいもないですよ。
タブレット端末を使うと、考える時間が増え発見をも増えるので楽しいです。「$x=0$付近では$x$が大事」これを念頭にして考えるようにします。
タブレット使いつつ、じっくり考えていきましょう。考えることが自然を知る為の道です。
4次関数で、グラフの形を変えるパラメータは三つ。3次関数では二つ、2次関数では一つ。なのに1次関数では0ではなく一つ、不思議。高次関数のグラフでは各項の係数をうまく調節することで定数項なくても平行移動できることはびっくりでした。
不思議ですね、でも納得できましたか?
こんなに深く1次関数、2次関数3次関数について考えたことがなかったのでとても不思議に感じました。
これから出てくるいろんな関数についても、深く考えていきましょう。
平行移動とかパラメータの詳しい話が初めてちゃんと理解できた。
それはよかったです。
1次関数から4次関数までの特徴がわかった。
よく理解しておきましょう。
計算する上ではわかっていた関数の平行移動の仕方を、さらにその理屈を知ったことでより深い理解をすることができた。
理屈を知ることは大事ですよ。
出身はどちらですか?。5/7の授業は仕事のため欠席させてください。
神戸生まれです。5/7には、たまたまこの授業は最初から休みです(木曜日だけど月曜日の授業をやる日になってます)。
xが0付近のときは$x^2$より$x$の方に注目することが大事ということがわかった。
その考え方、大事です。
自然科学において数学がどのような役割をするのかが意識できたと感じました。$n$次関数について、多項式関数について、式をミクロな視点でも見ていけるようにしたい。
ミクロな(あるいは「近所のみを見る」という意味で「ローカルな」)視点というのは自然科学でとても大事な考え方なのです。
2次関数のグラフで、1次の負のパラメータを変化させると頂点が放物線を描きながら移動していくのがおもしろかった。
どうしてそうなるのか、を式からも理解してみてください。
xの冪での$x,x^2,x^3$の需要度があまり実感できなかったけど、アニメーションで動かしてみて実感できた。自然科学のための数学というものが何か、わかってきた気がする。
関数やグラフを「実感できる」形で理解していきましょう。
形を決めるパラメータという考え方が新しくてまだなれない感じがしました。
慣れて下さい。新しいことを知り、使えるようになっていかないと。
関数の性質が少しわかった。それぞれの次数の係数が何に関係しているのか知れてよかった。
この「少し」の部分は、関数の持っている情報の中で一番大事な部分なのです。
xの1次と2次の係数が関数の大まかな形を決めるということがわかった。
より細かな部分を決めようとすると、高次の項が必要になってきます。
今まで考えたこともないような内容だった。
式のそれぞれの部分とグラフの形と、結びつけて考えることは大事ですよ。
前半は眠くてあまり授業に集中できませんでした。次回はしっかり睡眠取ってどんどん質問していきたいです。
元気を出そう!
自分の勉強してきたことと照らしあわせて確認できました。
一つ一つ確認しながら進んでください。
x=0付近ではxが大事とか、最初は意味がわからなかったけど、グラフで見てみるとなんとなく言いたいことがわかった。
グラフを思い浮かべながら、イメージをつけてください。
1次関数の平行移動した時に、yにa平行移動するのとxに-1平行移動するのは同じだということに初めて気がついた。
1次関数の特殊なところです。
グラフ全体を見ていると何が起こっているのかよく分からなくても、0付近をみると初めて発見できることが多くあった。
その考え方は大事です。付近を見る、つまり「ローカル情報」を見ることで法則が見えることがよくあります。
パラメータの話が気になっていたけど、最後になっとくできてよかった。
納得できてよかったです。
グラフとアンドロイドでイメージができました。
数式だけでなくイメージで理解するようにしましょう。