自然科学のための数学2015年度第24講
パラボラアンテナ


このおもちゃと同じ原理が衛星放送などの受信アンテナに使われている。アンテナは遠方からやってきたほぼ平行な電波を反射させ、一点(焦点)に集める。${x}$軸正方向からきた平行光線を原点に集めるようにするためには、鏡をどのような形に並べればよいか?---これを求めようとすると、微分方程式の手助けが必要になってくる。
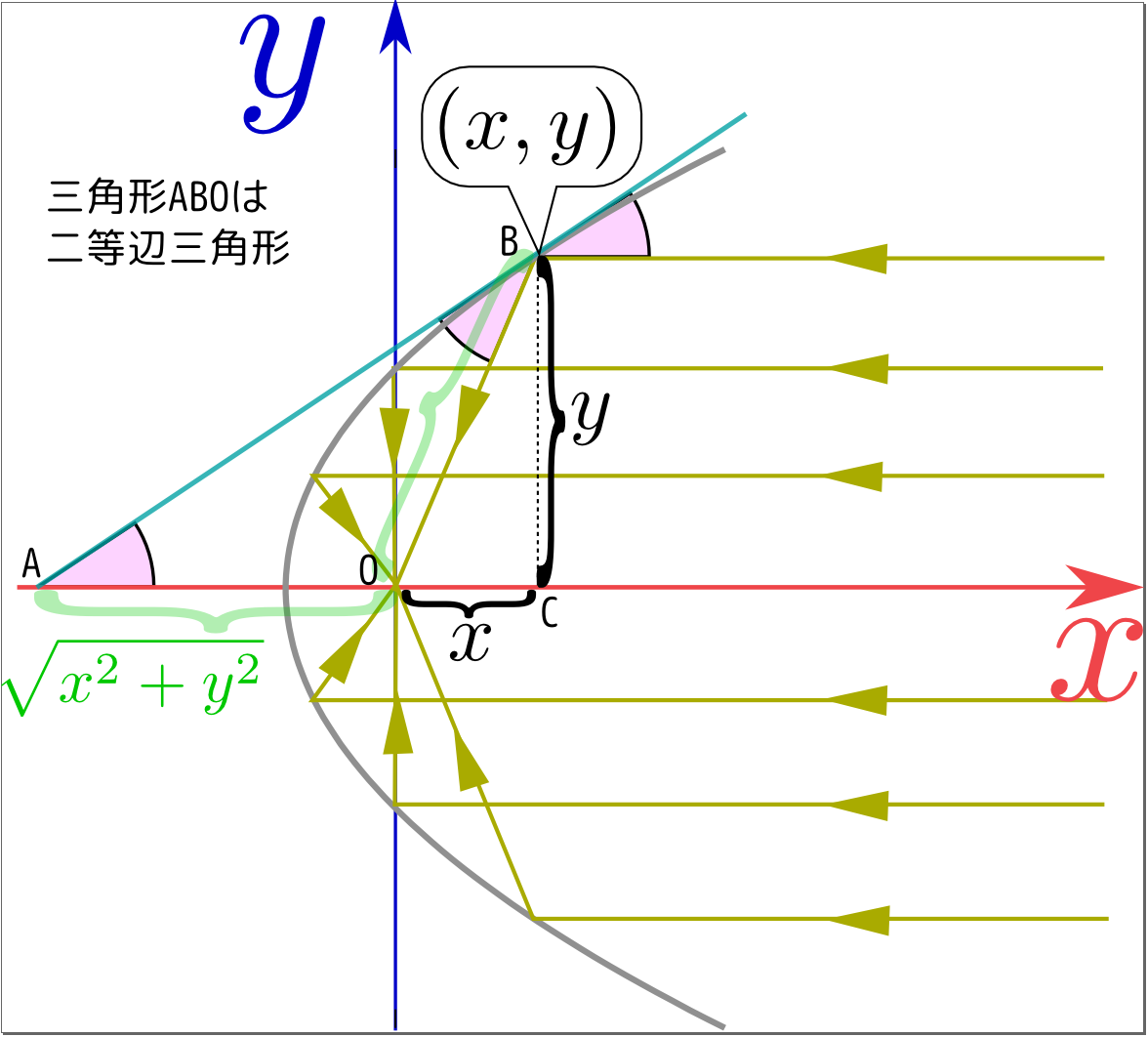
電波もしくは光が入射してきて、曲面の鏡に反射した後O点に集まる、という状況を考えよう。点Bで反射した光がOに向かうためには、鏡の反射の性質(入射光と反射光の鏡面に対する角度が等しい)から、図の$\angle$BAOと$\angle$ABOが等しくならなくてはいけない。よって図の三角形ABOは二等辺三角形であり、AO=BO=$\sqrt{{x}^2+{y}^2}$と書くことができる。以上から図に描き込んだように各部の長さを求めていく。点Bにおける鏡の傾き$\left({\mathrm dy\over \mathrm dx}\right)$は$\angle$BACの傾きであり、直角三角形BACの底辺ACは${x}+\sqrt{{x}^2+{y}^2}$であり、高さBCは${y}$なので、 \begin{equation} {\mathrm dy\over \mathrm dx}={{y}\over {x}+\sqrt{{x}^2+{y}^2}} \end{equation} が成り立つ。この式は分母の方が煩雑なので、 \begin{equation} {\mathrm dx\over \mathrm dy}={{x}+\sqrt{{x}^2+{y}^2}\over {y}} \end{equation} と逆数を取って${x}$を従属変数とした方が楽そうだ。さらに、この式は同次方程式だから \begin{equation} {\mathrm dx\over \mathrm dy}={{x}\over {y}}+\sqrt{\left({{x}\over {y}}\right)^2+1} \end{equation} と直し、${u}={{x}\over {y}}を変数とした方がよい。
${x}={u}{y}$としてから微分することで$\mathrm dx = \mathrm du{y}+{u}\mathrm dy$という関係式が出るので、 \begin{equation} \begin{array}{rl} {y} {\mathrm du\over \mathrm dy}+{{u}}=&{{u}}+\sqrt{{u}^2+1}\\ \end{array} \end{equation} となって後はこれを変数分離した${\mathrm du\over \sqrt{{u}^2+1}}={\mathrm dy \over {y}}$を積分すればよい。
$\sqrt{{u}^2+1}$が出てきた時の定番の一つとして、${u}=\sinh {t}$と置く。
- 試行錯誤(トライ&エラー)の繰り返しで見つけるもの
- ある程度「場数」を踏むと「あ、またこれか」という気分になるもの
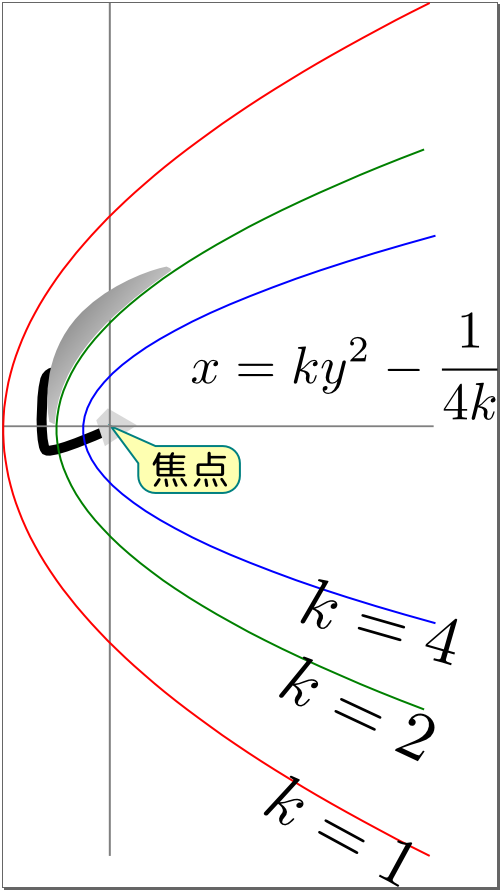
こうして$\sqrt{{u}^2+1}=\sqrt{1+\sinh^2 {t}}=\cosh {t}$、$\mathrm d u=\cosh {t} \mathrm dt$と置き換えられて、 \begin{equation} \begin{array}{rl} \int \mathrm dt =& \int {\mathrm dy\over {y}}\\[3mm] {t}=& \log {y}+C\\ \end{array} \end{equation} と積分ができる。${u}=\sinh {t}$だったから、これに上の${t}$を代入する。$\sinh {t}={\mathrm e^{{t}}-\mathrm e^{-{t}}\over 2}$で、$\mathrm e^{{t}}=\mathrm e^C {y}$であるから、 \begin{equation} \begin{array}{rll} {u}=& {\mathrm e^C {y}-{1\over \mathrm e^C{y}}\over 2}&{両辺に{y}を掛けて}\\ \underbrace{{u}{y}}_{{x}}=& {\mathrm e^C{y}^2-{1\over \mathrm e^C}\over 2}\\ \end{array} \end{equation} と答えを出す。未定のパラメータである$\mathrm e^C$を$\mathrm e^C=2k$と書きなおして \begin{equation} {x}=k{{y}}^2 - {1\over 4k} \end{equation} というのが答である。途中の積分が面倒な割には、答は単純な横倒しの放物線である。ちなみに「パラボラアンテナ」の「パラボラ」とは放物線のことである実際に衛星放送のアンテナなどに使われている曲面は放物線を回転させた面の一部であり、図に描き込んであるようにアンテナの中心と放物線の軸はずらしてある。。