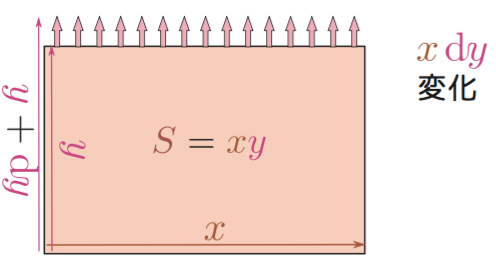青字は受講者からの声、赤字は前野よりの返答です。
二変数関数の微分によって立体を微分することができるとなり、すごいと思った。
「立体を微分している」というのとはちょっと違うかもしれないけど、曲面の傾きを求めているのは確か。
偏微分のおかげでもっと楽しく数学ができそうです。たくさん手を動かして早く慣れたいと思います。
こういう計算が楽しくできるようだと、この先もっともっと楽しくなっていくと思います。
偏微分はなんとかわかったけどすぐ忘れないように練習してできるようになりたい。
手を動かして忘れぬうちに頭と身体に刻みつけてください。
偏微分は他の授業でもやっていて今回の授業を通してさらに理解が深まった。アンドロイドで実際に見るとすごさがより伝わった。
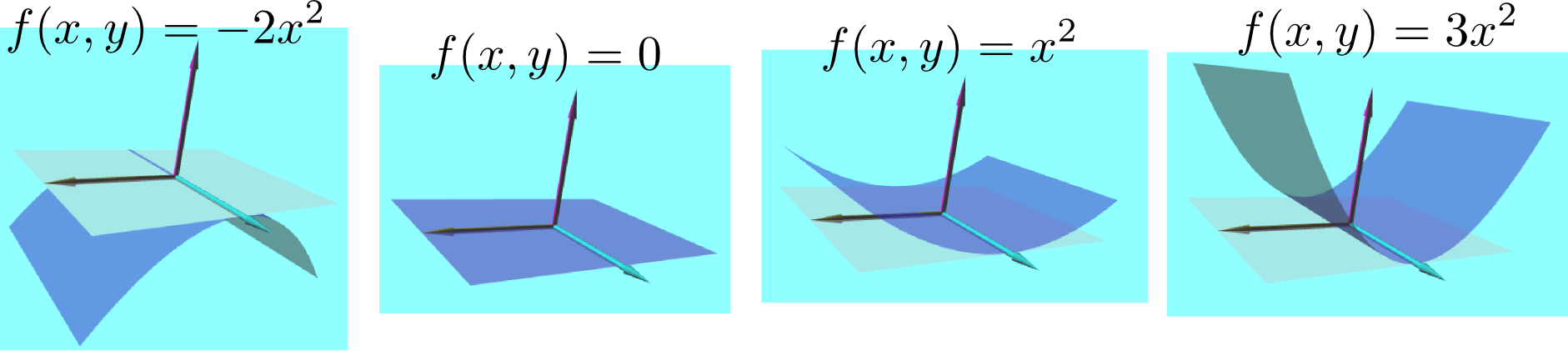
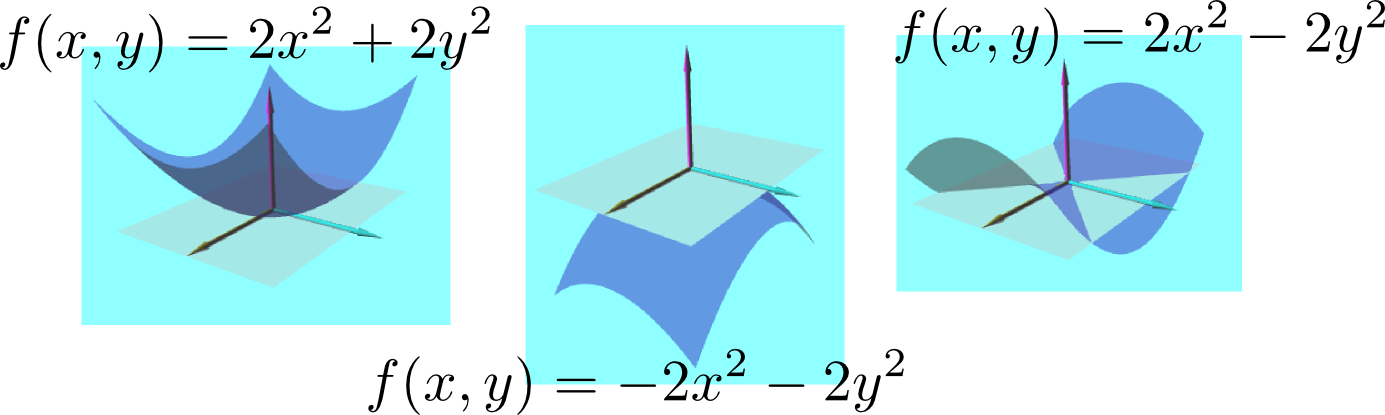
立体的図形で2変数関数を理解しておきましょう。
パーシャルといえばパーシャルデントですが、総入れ歯は何というんでしょうか? exactデントになるんでしょうか?
「フルデント」の方が意味的にはあっているな。
今日の偏微分は他の授業でもやったことがあるのですが、今日はその復習みたいな感じで理解が深まったと思う。
他のとも合わせて理解しておきましょう。
多変数ってだけで難しそう…と思ってましたが、片方を固定するだけで1変数とあまり変わりはしないのかなと思いました。
今日の範囲だとあまり差はわかりませんが、この先でいろいろ違いが見えてきます。
多変数関数や偏微分について学んだ。2変数関数についてアンドロイドの図を用いてわかった。
多変数関数のイメージをつけておいてください。
クリスマスが近いので復習します。
クリスマスがどう関係するのかがわかりませんが、復習するのはよいことです。
とても寒くなってきたので体調に気をつけたい。
元気に数学を!
偏微分 yを定数としてとく。
いや、定数にするのはyとは限らない。
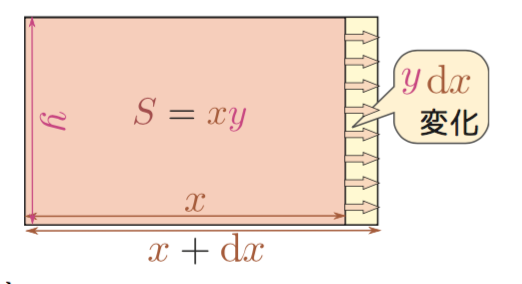
長方形の面積がグラフにすると曲面になることが面白いと思った。身の回りにグラフが曲面で表されるような2変数関数はどのくらいあるのかと思っていたけど結構あってウケた。
むしろ平面になる方が「幸運」って感じです。
変数が2個出てきて、基礎のところはとても大事なのでしっかりおさえたい。
まずは偏微分の意味と定義をしっかりと。
学科の授業で量子力学を学んでいるが、偏微分でなんで片方を定数とみていいのかすらわからなかった。今日2変数関数を空間でみて傾きを2方向で考えるというので少しすっきりした。
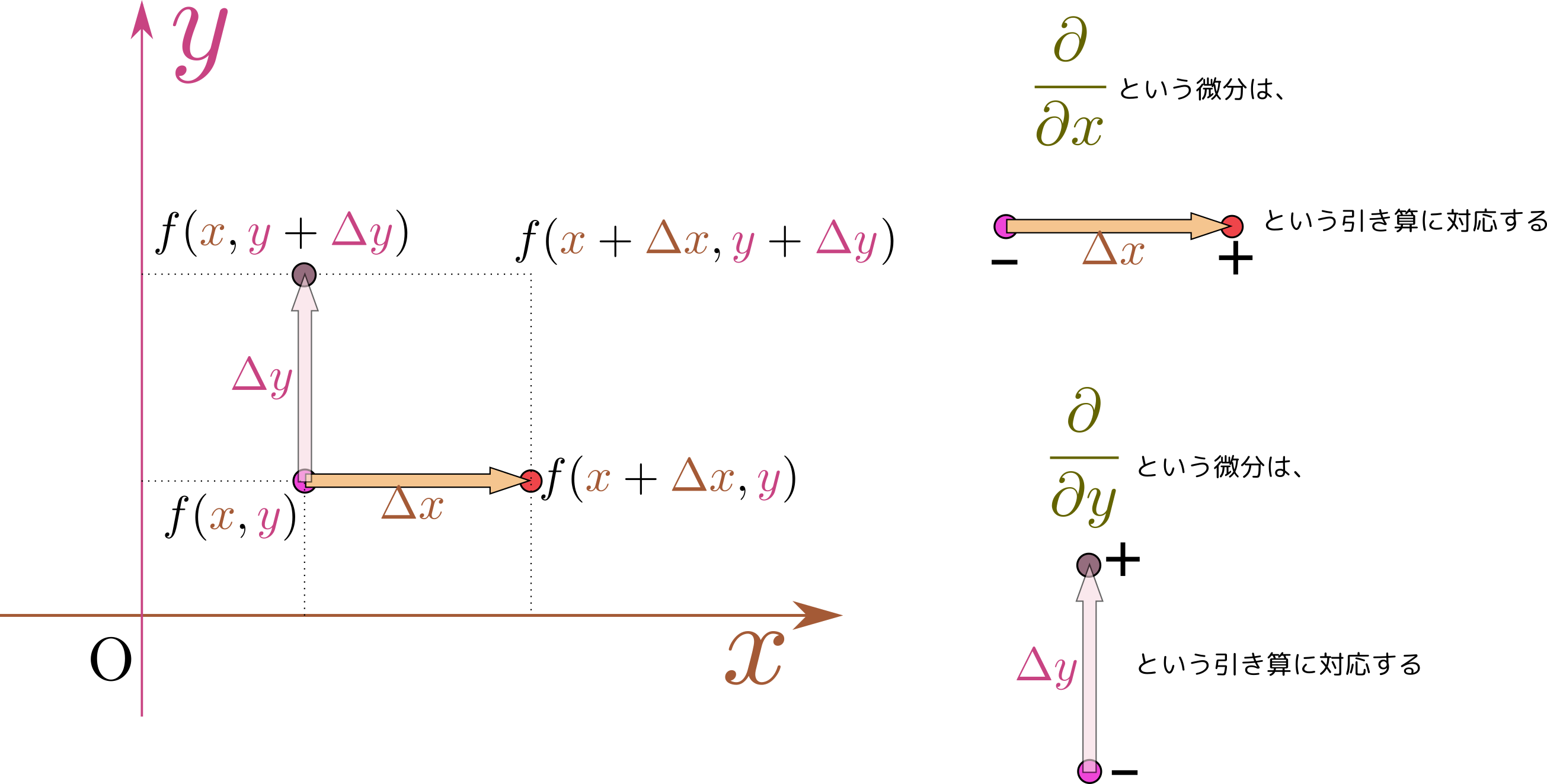
「微分に方向がある」というのが肝心です。
偏微分は難しいというイメージがありましたが、$x$を変数とするときは$y$を定数、$y$を変数とするといは$x$を定数とする考えの下で微分すると、思っていたよりも簡単に解くことができました。
偏微分の難しい部分は実はこの後出てきます。気をひきしめて。
前期で習ったような図形もでてきたし、最近物理数学IIで習った∂を利用して計算までしたし、偏微分の使い方に慣れようと思った。
偏微分はこれから先ずっとお世話になるので、慣れておきましょう。
偏微分は他の授業で習っていたけれど、詳しく説明されなかったので、今回詳しく知ることができて良かったです。
偏微分はよく使うので、中身までしっかり理解しておきましょう。
1限がテストで疲れました。
お疲れ様。
2変数関数を実際目でみて確認することができて、どのパラメータを動かせばグラフがどう動くかのイメージが分かったので良かった。
そのイメージ、大事です。
大きさのある物体の自由度が6というのは以前から聞いていたが、今日の説明でようやくすっきりした。
その辺の物体グルグル回して確認してください。
頭の中ではややこしいですが、数式で表すとわかりやすくなりました。∂の読み方ですが私はラウンドとします。
数式は概念を整理するのに便利ですね。
微積の講義でも偏微分に入って、少しわかりにくい部分があったけど今回でイメージしやすくなったと感じました。
それはよかった。微積の方もしっかり理解してください。
偏微分は流体力学で出てきた。海流系の流体力学で、${\mathrm d\over \mathrm dt}$と${\partial \over \partial t}$が出てきた時、何が違うのか最初はわからなかったが、使い方だけ理解していた。今日、偏微分というものがやっとわかった気がする。
二つの微分の違いは、「他の変数を固定して」というのがないかあるかですね。本質的なところをしっかり理解しておきましょう。
偏微分はこうやって解くのだと理解することができました。
今日はとりあえず偏微分の意味と計算の方法まででした。こっから先でどんどん応用していきましょう。
偏微分は他の講義でも何度かやっていたけど、今日は詳しく知ることができました。図解でより納得できました。
図でイメージしておきましょう。
偏微分は便利そうだけど、変数の数が増えたら面倒になりそう。
しかし、変数が多いときこそ偏微分が重要です。
偏微分が他の授業で出てきてわからなかったけど、この授業で細かく説明してくれるので理解することができました。まだまだ序盤なので頑張ります。
はい、この後本番が来ます。
偏微分のときの∂の名前を知らなかったのでどのパターンで言われてもわかるようにしたい。
いろいろ読み方はありますが、どれでも対応しましょう。
今日はテストが1限だったから疲れた。
お疲れ様。
他の講義で偏微分をやったときあいまいであったが、今回で理解し得た。
あいまいなところは残しちゃダメですよ。
偏微分の意味がわからなかったが、定義を知ったことでよくわかった。
どんな数学的概念も、定義と「なんでそんなものを定義したいのか」という部分がわかれば、だいたいわかります。
偏微分は名前だけは聞いたことがあって難しそうだという印象を持っていたが、片方を定数のように考えてしまえば、今のところは解きやすかった。
これから先も理解していってください。
新たに学んだ微分学の「偏微分」は見た感じ難しそうだったが、実際は微分する式が増えただけで、そこまで困ることはなかった。今日は簡単な式だったが、これが「微分方程式」と融合するととても大変な計算になりそう。
まぁ大変は大変ですが、なんとかなります。がんばって。
もし2変数が$n$変数なら…。
$$
f(x+\Delta x,y+\Delta y,z+\Delta z,\cdots)=f(x,y,z,\cdots)+{\partial f\over\partial x}\Delta x+{\partial f\over\partial y}\Delta y+{\partial f\over\partial z}\Delta z+\cdots
$$
にして、${\Delta F\over \Delta x+\Delta y+\Delta z+\cdots }=$(アンサー) こんな感じの数学言語なのか?
分母で足し算することはなくて、${\Delta f\over \Delta x},{\Delta f\over \Delta y},{\Delta f\over \Delta z},\cdots$と$n$個の偏微分を考えます。
 と
と