自然科学のための数学2015年度第26講
常微分と偏微分
微分の表現として、$f({x}+\mathrm dx)=f({x})+f'({x})\mathrm dx$もしくは、$\mathrm df=f'({x})\mathrm dx$という書き方具体例で示せば、$\cos ({x}+\mathrm dx)=\cos {x}-\sin{x}\mathrm dx$もしくは$\mathrm d (\cos{x})=-\sin{x}\mathrm dx$など。があったが、それの偏微分のバージョンは \begin{equation} \begin{array}{c} f({x}+\mathrm dx,{y}+\mathrm dy) =f({x},{y})+ \left({\partial {f({x},{y})}\over \partial x}\right)_{\!\!{y}}\mathrm dx +\left({\partial {f({x},{y})}\over \partial y}\right)_{\!\!{x}}\mathrm dy\\[6mm] もしくは\\[3mm] \mathrm df({x},{y})=\left({\partial {f({x},{y})}\over \partial x}\right)_{\!\!{y}}\mathrm dx +\left({\partial {f({x},{y})}\over \partial y}\right)_{\!\!{x}}\mathrm dy \end{array}\label{zenbibun} \end{equation} となる。上の例に則して書けば、 \begin{equation} \begin{array}{rll} \mathrm d \overbrace{({x}^2{y})}^{f({x},{y})}=&\overbrace{2{x}{y}}^{\left({\partial {f({x},{y})}\over \partial x}\right)_{{y}}}\mathrm dx&+\overbrace{{x}^2}^{\left({\partial {f({x},{y})}\over \partial y}\right)_{{x}}} \mathrm dy\\[2mm] \mathrm d\overbrace{ (\sin({x}+{y}^2))}^{f({x},{y})}=&\overbrace{\cos({x}+{y}^2)}^{\left({\partial {f({x},{y})}\over \partial x}\right)_{{y}}}\mathrm dx &+ \overbrace{2{y}\cos({x}+{y}^2)}^{\left({\partial {f({x},{y})}\over \partial y}\right)_{{x}}}\mathrm dy \end{array} \end{equation} となる。新しい記号を使ってはいるが、この計算は別に目新しいものではない。偏微分は単に「本当は定数である文字を定数とみなして微分する」というだけで計算テクニックとして難しい点は無い(偏微分ならではの難しさは現段階ではまだ出てきていない。後で登場する)。
大事なことは、ここで$\mathrm dx$と$\mathrm dy$の割合を変化させることで、$xy$平面上のいろんな方向の変化量(いろんな方向への微分)が表現できるということ。一階微分では「微分の方向」は本質的には一つしかなかった。二階微分では「$x$方向」「$y$方向」の二つの独立した微分の方向が出てくる。
二階偏微分と多変数関数の極大極小
偏微分も常微分同様、二階微分がある。その記号も \begin{equation} \left( {\partial\over \partial x} \left({\partial {f({x},{y})}\over \partial x}\right)_{{y}} \right)_{{y}} =\left( {\partial^2 {f({x},{y})}\over \partial x^2}\right)_{{y}} ,~~ \left( {\partial\over \partial y} \left({\partial {f({x},{y})}\over \partial y}\right)_{{x}} \right)_{{x}} =\left( {\partial^2 {f({x},{y})}\over \partial y^2}\right)_{{x}} \end{equation} のように常微分の場合に似た書き方にする(三階以上も同様である)。これら二つの偏微分が(それぞれ${x}$方向と${y}$方向の)曲がり具合を表現しているのは、1変数の場合と同様である。
偏微分の一階微分は、独立なものは($x$方向と$y$方向の)二つある。
では偏微分の二階微分はどうだろう。まずはこんな表を作ってみよう。
$$ \begin{array}{ccccc} x^3y^2&{{\partial\over\partial x}\atop\rightarrow}&3x^2y^2&{{\partial\over\partial x}\atop\rightarrow}&6xy^2\\ {\partial\over\partial y}\downarrow&&{\partial\over\partial y}\downarrow&\\ 2x^3y&{{\partial\over\partial x}\atop\rightarrow}&6xy\\ {\partial\over\partial y}\downarrow&\\ 2x^3& \end{array} $$
ここで、「${\partial \over\partial x}$してから${\partial\over\partial y}$」と「${\partial \over\partial y}$してから${\partial\over\partial x}$」が一致することに注意。
$x$の二階微分の結果の$+2$の部分を忘れている人が多かった。$2x\mathrm e^{x^2}\cos y$を$x$で微分するのだから、最初の$2x$の$x$も微分される。
偏微分の二階微分の独立なものには、 \begin{equation} \left( {\partial\over \partial x} \left({\partial {f({x},{y})}\over \partial y}\right)_{{x}} \right)_{{y}}={\partial^2 {f({x},{y})}\over \partial x \partial y} \end{equation} のように「最初に${y}$で微分、次に${x}$で微分」もある(上の式の右辺は固定する変数を省略する書き方を使った)。分母の書き方が常微分と決定的に違うところなので注意しようここで、${\partial^2 {f({x},{y})}\over \partial x\partial y}$と${\partial ^2 {f({x},{y})}\over \partial y\partial x}$は違うのか?---という疑問を持った人もいるだろう。微分可能な関数に対してはこの二つは等しい。それは、上の式が${x}\leftrightarrow{y}$の取り換えに対して対称であることからもある程度納得できる。詳しくは後で説明するので、しばらくの間は「そういうものだ」と思って進めよう。。
定義にしたがって計算すれば、この二階微分は \begin{equation} \begin{array}{rl} & \lim_{{\Delta x}\to0\atop{\Delta y}\to0} {\left( f({x}+{\Delta x},{y}+{\Delta y}) -f({x}+{\Delta x},{y})\right) -\left(f({x},{y}+{\Delta y}) -f({x},{y}) \right) \over {\Delta x}{\Delta y}} \\ = & \lim_{{\Delta x}\to0\atop{\Delta y}\to0} { f({x}+{\Delta x},{y}+{\Delta y}) -f({x}+{\Delta x},{y}) -f({x},{y}+{\Delta y}) +f({x},{y}) \over {\Delta x}{\Delta y}} \end{array}\label{delxdely} \end{equation} という量を計算している。図で描くと、
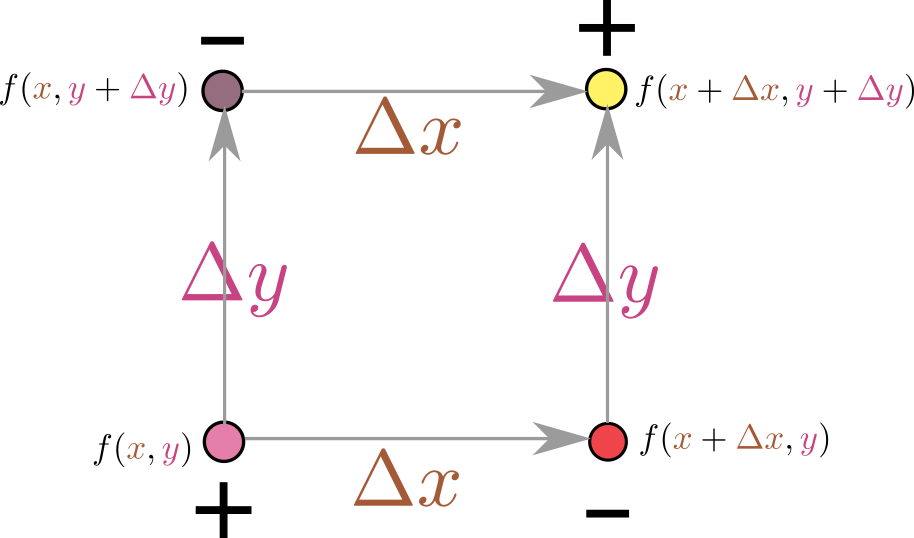
のような足算を行っている。
この二階微分も曲り具合を表現している。
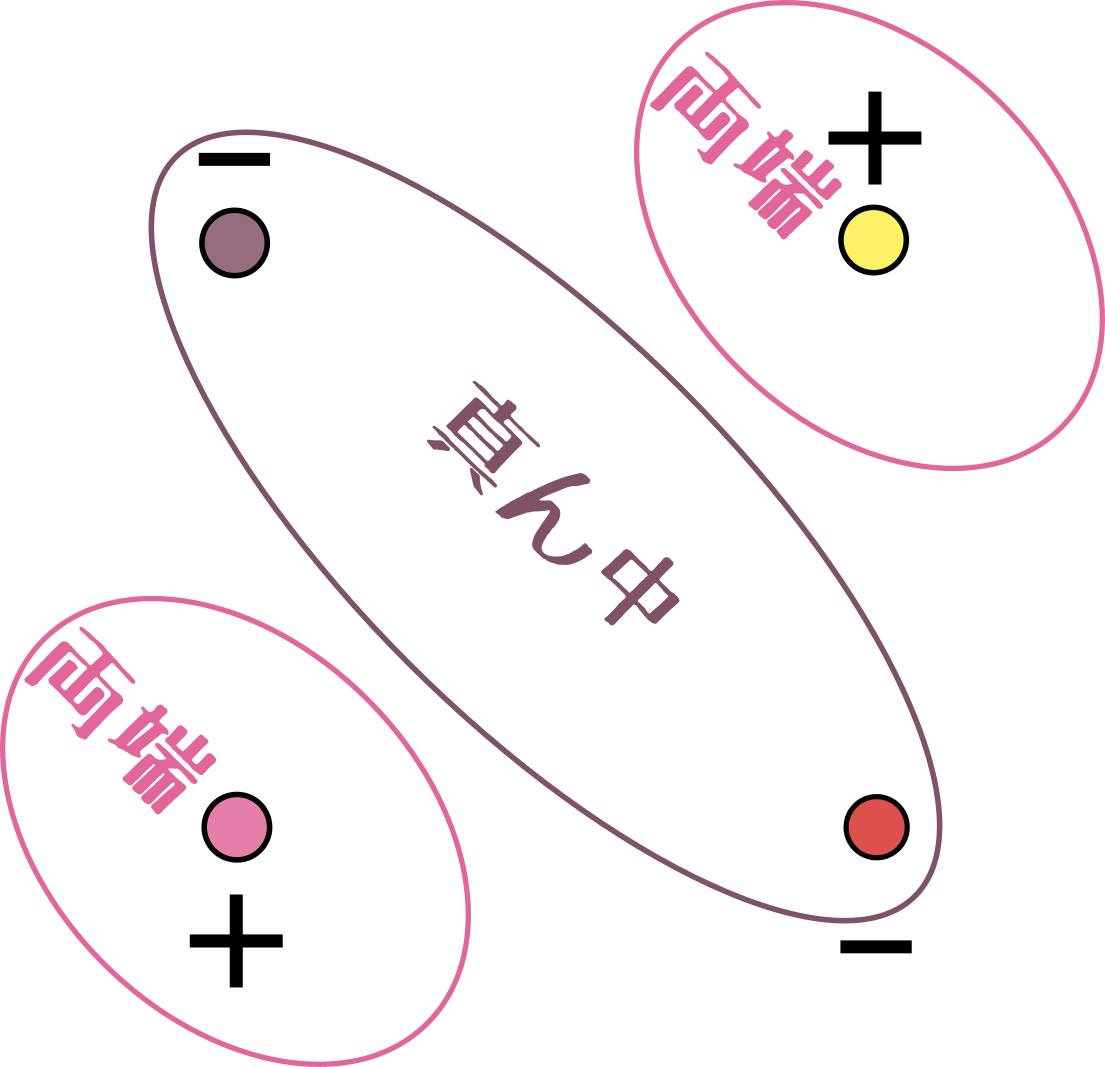 または
または
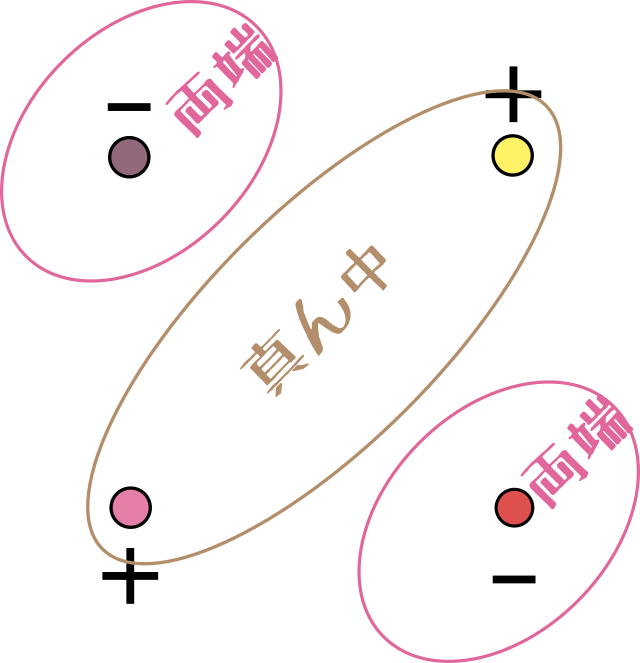
のように考えると、斜め方向に見ての「真ん中」と「両端」で引算をしていることがわかる前に二階微分を考えた時は「両端の平均」と「真ん中」で考えたが、ここでは2点と2点の対等な差を考えているから平均操作はいらない。。
1変数関数の極大・極小点では微分が0になったが、多変数(ここでは「2変数」のみを扱う)関数の場合も微分が0の点が極大極小点になるのは同じである。ただし、多変数なら「微分の方向」があるので「ある方向の微分は0だが、別の方向では0でない」ということが起こりえる。
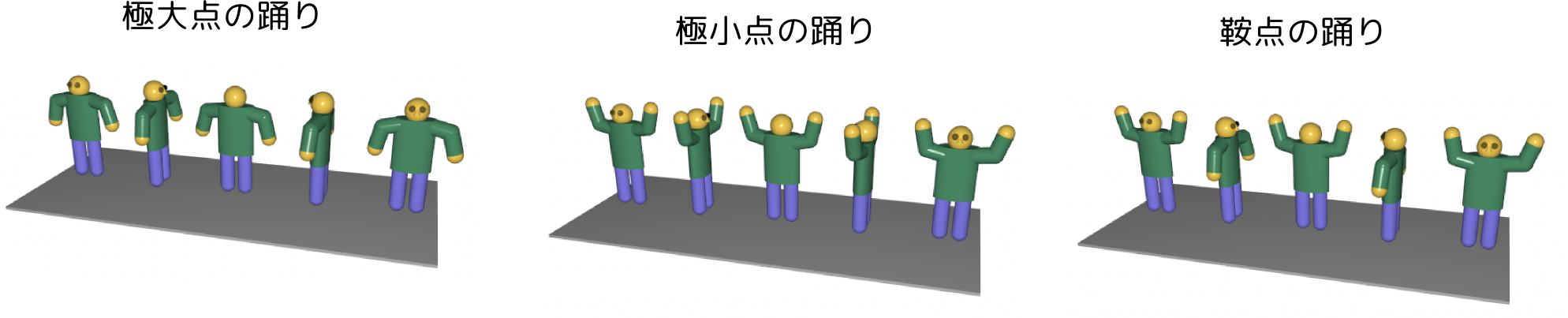
次の図に示したのは$f({x},{y})={x}^2+{y}^2,-{x}^2-{y}^2,{x}^2-{y}^2$の三つの関数の3次元グラフで、どの場合も原点においてどの方向の微分も0であるが、二階微分の値の正負が違う。
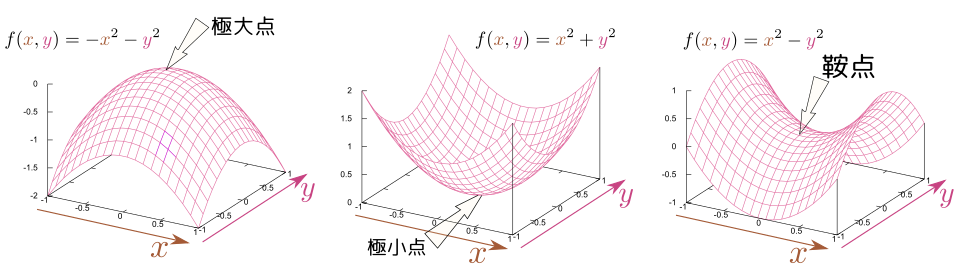
どの方向に対しても一階微分が0で二階微分が負なら、それは極大点である。逆に、どの方向に対しても一階微分が0で二階微分が正なら、それは極小点である(ここまでは1変数の時の素直な拡張である)。多変数で現れる新しい状況として「一階微分はどの方向に対しても0であるが、二階微分の正負は方向により異なる」という場合があり、この場合は(図に示したように馬の鞍の形なので)「鞍点(suddle point)」と呼ぶ。
上では比較的単純な例を提示したので、${\partial^2 {f}\over \partial x^2}$と${\partial^2 {f}\over \partial y^2}$の正負を見て場合分けできたが、2変数関数の二階微分はもう一つ、${\partial^2 {f}\over \partial x\partial y}$もある(上の例では全て${\partial^2 {f}\over \partial x\partial y}=0$なので気にしなくてもよかった)。

逆に${\partial^2 {f}\over \partial x\partial y}\neq0$である例として、$f({x},{y})={x}{y}$を考えてみると、この場合も鞍点になっている実はこのグラフは$f({x},{y})={x}^2-{y}^2$を${\pi\over 4}$だけ回転して、少し高さを調整したものになっている。。
一般の2変数関数で、一階微分が全て0である点(このような点は「停留点」と呼ぶ停留点の中には、極大点と極小点と鞍点が含まれる。)が見つかったとして、その点が極大なのか極小なのかそれとも鞍点なのかを知りたい「別にそんなの知りたくない」って?---この関数がたとえば貴方の所有している財産の価値だったら、「ここが極大かどうか」を知りたくならないかな?場合は、テイラー展開の2次の項を調べる必要がある。
$(a,b)$が停留点とすればそこで一階微分は0だから、$({x}-a)={\Delta x},({y}-b)={\Delta y}$と書けば、 \begin{equation} f({x},{y}) =f(a,b) +\overbrace{\underbrace{{1\over 2}{\partial^2 {f}\over \partial x^2}}_a({\Delta x})^2 +\underbrace{{\partial^2 {f}\over \partial x\partial y}}_b{\Delta x}{\Delta y} +\underbrace{{1\over 2}{\partial^2 {f}\over \partial y^2}}_c({\Delta y})^2}^{曲がり具合を表現する部分} +\cdots \end{equation} となる。3次以上の項は省略した。式に示したように、係数を以下$a,b,c$で表す。
上の「曲がり具合を表現する部分」がどのような${\Delta x},{\Delta y}$に対しても正であるならばこの点は極小点、逆に常に負ならば極大点である。正にも負にもなる場合は鞍点だと言える(他の可能性としては正、負ではなく0以上や0以下という可能性もある)。この式は \begin{equation} a({\Delta x})^2 + b{\Delta x}{\Delta y}+c({\Delta y})^2 =\underbrace{({\Delta y})^2}_{常に正}\underbrace{ \left( a\left({{\Delta x}\over{\Delta y} }\right)^2 +b{{\Delta x}\over{\Delta y} }+c \right)}_{この部分の正負が問題} \end{equation} となるから、後は「二次式$a{x}^2+b{x}+c$の正負を場合分けせよ」という問題${{\Delta x}\over{\Delta y} }$の変域は実数全体である。${\Delta x}=a\cos\alpha,{\Delta y}=a\sin\alpha$と置けば、${{\Delta x}\over{\Delta y} }=\cot \alpha$となる。になり、
- $b^2-4ac>0$ の場合: 正にも負にもなる(鞍点)
- $b^2-4ac<0$かつ$a>0$の場合: 常に正(極小点)
- $b^2-4ac<0$かつ$a<0$の場合: 常に負(極大点)
のように二次方程式の判別式を使うこととで状況を分類することができる$b^2-4ac=0$の場合は省略したが、正(もしくは負)が0以上(もしくは0以下)になるという違いである。。