自然科学のための数学2015年度第27講
全微分と偏微分
「関数$f(x,y)$の微小変化」を表す量は、以下の式のように書ける。
関数$f(x,{y})$の全微分
\begin{equation} \mathrm df(x,y)=\left({\partial {f(x,{y})}\over \partial x}\right)_{y}\mathrm dx+\left({\partial {f(x,{y})}\over \partial y}\right)_{x}\mathrm dy \end{equation}
この$\mathrm d\left(?\right)$という形の式を「?の全微分(exact differential)」あるいは「完全微分」、「total differential」という呼び方もある。と呼び、こういう形の式は「全微分形(exact)あるいは「完全微分形」。英語の形容詞は「exact」だが日本語では「微分」を補って使う場合が多い。になっている」と言う。前に「偏微分には方向がある」と述べたが、「$x$方向の微分」と「${y}$方向の微分」の二つを含む$x$方向でも${y}$方向でもない「斜め方向の微分」については後で考える。。その全てを考えているので「全微分」と呼ぶこの章の前まで行ってきた1変数の微分では、方向が一つしかないから、全微分と偏微分を分ける必要はなかった。。全微分のうち「$\mathrm dx$の係数である$\left({\partial {f(x,{y})}\over \partial x}\right)_{{y}}$」を取り出したもの(${y}$方向も同様)が「偏微分」である。
ベクトルを$\vec A=A_x\vec {\mathbf e}_x+A_y\vec{\mathbf e}_y$と$x$成分と${y}$成分に分けて表現するように、全微分の「$x$成分のようなもの」が$\left({\partial {f(x,{y})}\over \partial x}\right)_{{y}}$、「${y}$成分のようなもの」が$\left({\partial {f(x,{y})}\over \partial y}\right)_{x}$である$\mathrm dx$や$\mathrm dy$が$\vec{\mathbf e}_x$や$\vec{\mathbf e}_y$のような単位ベクトルの役割を果たしている。と思ってよい。
上の式は(常微分のとき「$f(x)$の変化が$f'(x)\mathrm dx$」と書けたのと同様に)
$f(x,{y})$に起こる変化のうち、
$x$が変化したことによって起こる変化は$\left({\partial {f(x,{y})}\over \partial x}\right)_{{y}}\mathrm dx$と書け、
${y}$が変化したことによって起こる変化は$\left({\partial {f(x,{y})}\over \partial y}\right)_{x}\mathrm dy$と書ける。
というふうに「読む」べきである。あるいは、
$\mathrm dy=0$にしてから${\mathrm df\over \mathrm dx}$を計算したもの、すなわち \begin{equation} \begin{array}{rll} \mathrm df(x,{y})=&\left({\partial {f(x,{y})}\over \partial x}\right)_{{y}}\mathrm dx+\underbrace{{\left({\partial {f(x,{y})}\over \partial y}\right)_{x}\mathrm dy}}_{0にする}&{↓両辺を\mathrm dy で割る} \\ {\mathrm df(x,{y})\over \mathrm dy}=&\left({\partial {f(x,{y})}\over \partial x}\right)_{{y}} \end{array}\label{henbibunzeronisuru} \end{equation} という計算をした結果が$\left({\partial {f(x,{y})}\over \partial x}\right)_{{y}}$であり、同様に、
$\mathrm dx=0$にしてから${\mathrm df\over \mathrm dy}$を計算したものが$\left({\partial {f(x,{y})}\over \partial y}\right)_{x}$である、と考えてもよい。
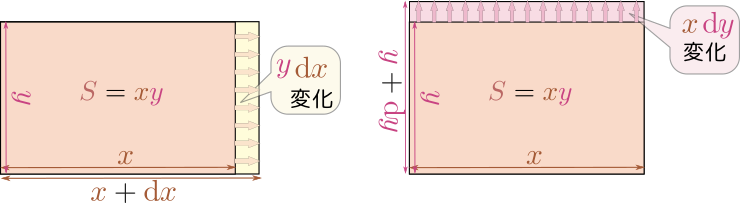
例1:${S}=x{y}$
横$x$、縦${y}$の長方形の面積は${S}=x{y}$だが、${S}$の全微分はライプニッツ則にしたがって \begin{equation} \mathrm dS=\underbrace{\mathrm dx {y}}_{xを微分した項}+ \underbrace{x\mathrm dy}_{{y}を微分した項} \end{equation} となる。$x$が$\mathrm dx$増加すれば、${y}\mathrm dx$だけ(${y}$が増加する場合は$x\mathrm dy$だけ)面積が増加する、ということを上の式は表している。
例2:${R}=\sqrt{x^2+{y}^2}$
$f(x,{y})=\sqrt{x^2+{y}^2}$という関数は、原点から点$(x,{y})$までの距離という意味のある関数である。
この式を微分すると、 \begin{equation} \mathrm d \left(\sqrt{x^2+{y}^2}\right)= {x\over\sqrt{x^2+{y}^2} }\mathrm dx +{{y}\over\sqrt{x^2+{y}^2} }\mathrm dy\label{Rzenbibun} \end{equation} である。
${x\over\sqrt{x^2+{y}^2} }$は$\sqrt{x^2+{y}^2}$を、${y}$は変化しないものとして、$x$で微分することで得られる。${y}$が変数であるということを一旦忘れて(なんなら$\sqrt{x^2+C^2}$のように定数$C$に置き直して考えて)、普通に$x$で微分という操作を行えばよい。${{y}\over\sqrt{x^2+{y}^2} }$は$x$と${y}$の立場が入れ替わっただけで、同様である。
この二つの微分の意味するところを図で表現したのが次の二つの図である。
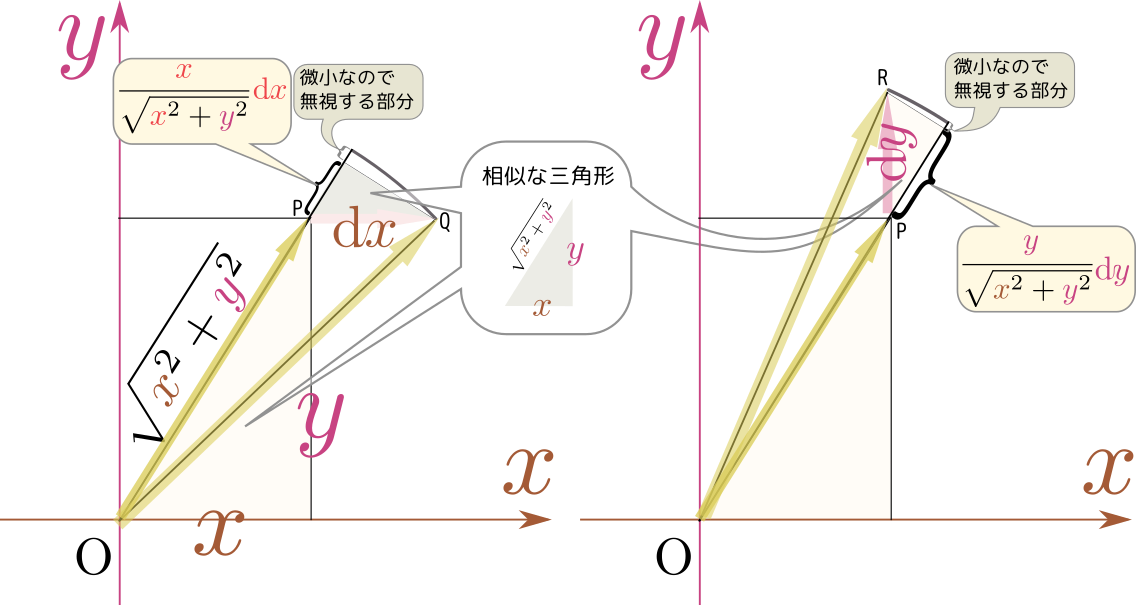
式で計算しても、図で考えても偏微分は計算できる(もちろん両者は一致する)
図には$x$方向と${y}$方向という二種類の変化のみを示したが、一般の方向を向く時は$\mathrm dx,\mathrm dy$の比が変わると思えばよい。$x$方向の微分は$\mathrm dx:\mathrm dy=1:0$、${y}$方向の微分では$\mathrm dx:\mathrm dy=0:1$である。斜め45度方向では$\mathrm dx:\mathrm dy=1:1(\mathrm dx=\mathrm dy)$である。
変数が独立でない場合の全微分
ここまでは、$x$と$y$が独立な変数である場合(当然、$\mathrm dx$と$\mathrm dy$も独立になる)を考えたが、この二つに関係がある場合を考えることもできる。
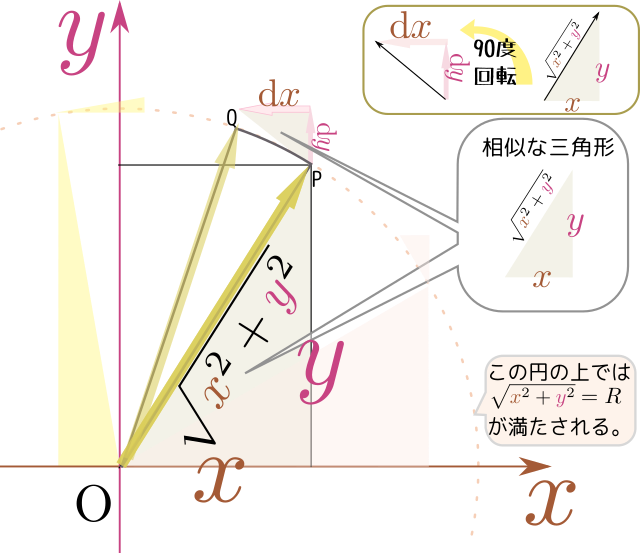
${x}$と${y}$が$\sqrt{{x}^2+{y}^2}$が一定であるという関係を持っている場合、${x}$と${y}$それぞれの変化量である$\mathrm dx$と$\mathrm dy$も独立ではない。$\sqrt{{x}^2+{y}^2}=R(一定)$を保ちつつ(グラフ上では、原点を中心とする半径$R$の円の上に乗りつつ)変化させた様子を描いたのが左の図である。
右の相似な三角形に注意すると、$\mathrm dx$と$\mathrm dy$の間に \begin{equation} {x}\mathrm dx+{y}\mathrm dy=0 \end{equation} という、全微分が0という条件$\left({{x}\over\sqrt{{x}^2+{y}^2 }}\mathrm dx+{{y}\over\sqrt{{x}^2+{y}^2 }}\mathrm dy=0\right)$と本質的に(両辺に$\sqrt{{x}^2+{y}^2 }$を掛ければ)同じ式が読み取れる。
この${x}\mathrm dx+{y}\mathrm dy=0$という式は、$({x},{y})\cdot \left(\mathrm dx,\mathrm dy\right)=0 $のように$\left(\mathrm dx,\mathrm dy\right)$というベクトル(図の$\overrightarrow{\rm PQ}$)と$\left({x},{y}\right)$(図の$\overrightarrow{\rm OP}$)というベクトルの内積が0(垂直)という式だと解釈することもできる。これは「円の接線」の性質に合致している。つまりこの$\sqrt{{x}^2+{y}^2}$を一定としての全微分は「${\theta}$方向の微分」になる。
ここでは、$\sqrt{x^2+y^2}$が一定であるという条件から、微分方程式$x\mathrm dx + y\mathrm dy=0$を出した。この逆はできるか??というのが次に考えたいことである。
なぜそんなことがしたいかというと、物理でのエネルギー保存則や運動量保存則のように「変化の前後で一定になる量」を見つけると計算が楽になったり見通しがよくなることが多い。「保存量」を見つけるということはつまり、$\mathrm d(?)=0$の形に式をまとめることなのである。