自然科学のための数学2015年度第28講
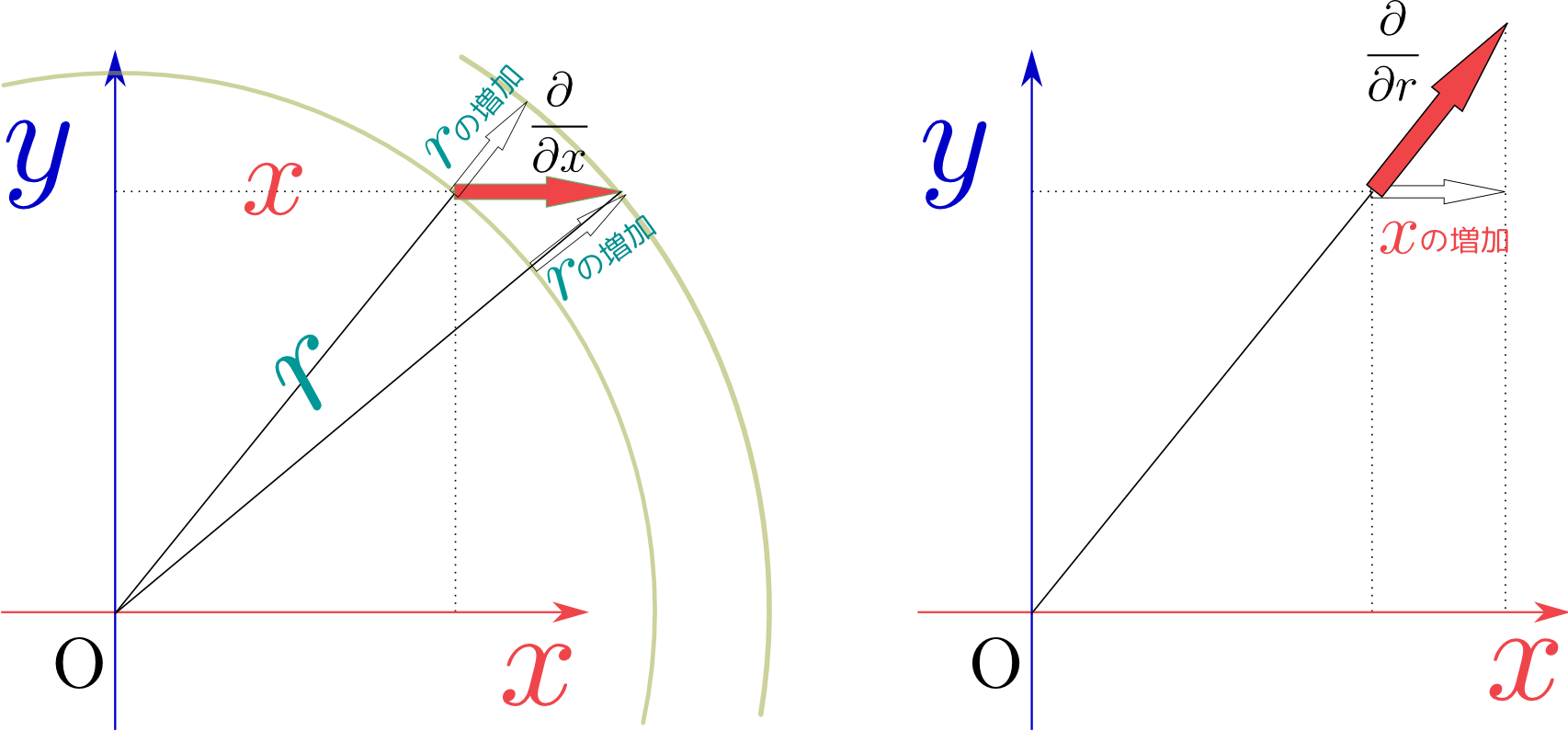
常微分と偏微分の違い(復習)
「関数$f(x)$の微小変化」を表す量は、以下の式のように書ける。 $$ f(x+\mathrm dx)=f(x)+{\mathrm df\over\mathrm dx}(x)\mathrm dx $$ あるいはこの逆にあたる演算が $$ f(x_1)=f(x_0)+\int_{x_0}^{x_1} {\mathrm df\over\mathrm dx}(x)\mathrm dx $$ である。積分しているのは下の赤矢印の部分。
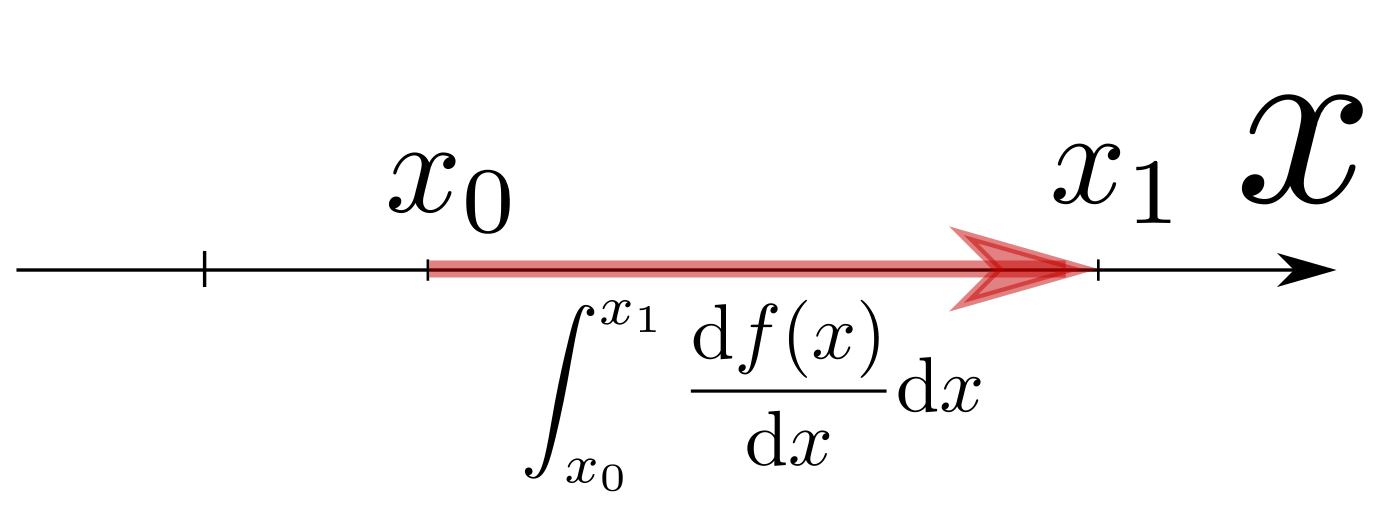
これは$f(x_0)$を「元の値」、$\int_{x_0}^{x_1} {\mathrm df\over\mathrm dx}(x)\mathrm dx$を「変化量」と見れば、$f(x_1)$が「変化後の値」となる、という式であり、関数の変化の様子を微分と積分で表現していることになる。
常微分(1変数)では変化は$x$が増えるか減るか、本質的には一つの方向しかない。
「関数$f(x,y)$の微小変化」を表す量は、以下の式のように書ける。 $$ f(x+\mathrm dx,y+\mathrm dy)=f(x,y)+{\partial f(x,y)\over\partial x}\mathrm dx+{\partial f(x,y)\over\partial y}\mathrm dy $$ この${\partial f(x,y)\over\partial x}\mathrm dx+{\partial f(x,y)\over\partial y}\mathrm dy$の部分を「全微分」と呼ぶわけである。
大事なことは偏微分には方向がある。ということである。
さて、常微分における「微分の逆」の演算 $$ f(x_1)=f(x_0)+\int_{x_0}^{x_1} {\mathrm df\over\mathrm dx}(x)\mathrm dx $$ の偏微分バージョン(2変数バージョン)を考えてみよう。単純に、 $$ U(x_1,y_1)=U(x_0,y_0)+\underbrace{\int_{x_0}^{x_1} {\partial U(x,y_0)\over\partial x}\mathrm dx}_{積分1}+\underbrace{\int_{y_0}^{y_1} {\partial U(x_0,y)\over\partial y}\mathrm dy}_{積分2} $$ と考えるのは正しいだろうか。これはどのような「積分」を行っていることになるか、図を描いて考えてみよう。
ここではしばらく図を描いて自由に討論しつつ考えてもらった。
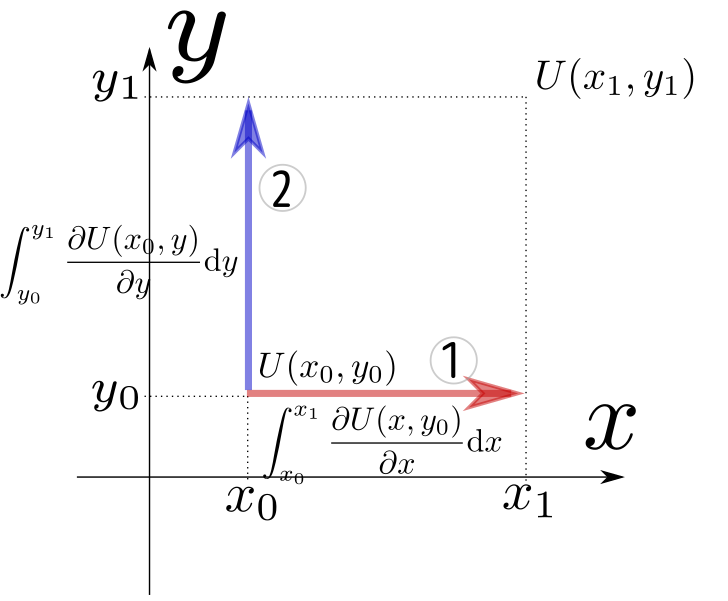
というような図を描いてみると「この積分は場所$(x_1,y_1)$に届いてない!」ことがわかる(だからこの計算で$U(x_1,y_1)$になるはずがない)。
$(x_0,y_0)$から出発してちゃんと$(x_1,y_1)$に届く積分としては、式で書けば $$ U(x_1,y_1)=U(x_0,y_0)+\underbrace{\int_{x_0}^{x_1} {\partial U(x,y_0)\over\partial x}\mathrm dx}_{積分1}+\underbrace{\int_{y_0}^{y_1} {\partial U(x_1,y)\over\partial y}\mathrm dy}_{積分3} $$ 図で書けば、
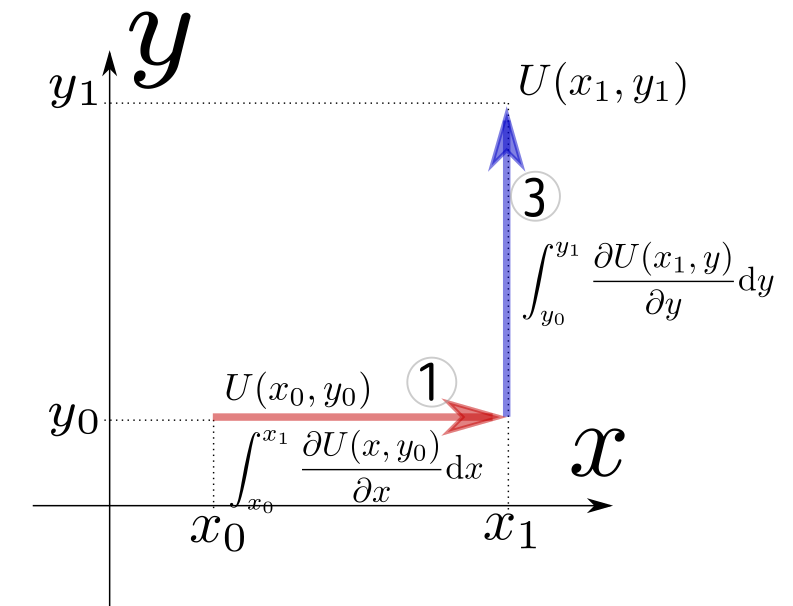
または、式で書けば、 $$ U(x_1,y_1)=U(x_0,y_0)+\underbrace{\int_{y_0}^{y_1} {\partial U(x_0,y)\over\partial y}\mathrm dy}_{積分2}+\underbrace{\int_{x_0}^{x_1} {\partial U(x,y_1)\over\partial x}\mathrm dx}_{積分4} $$ 図で書けば、
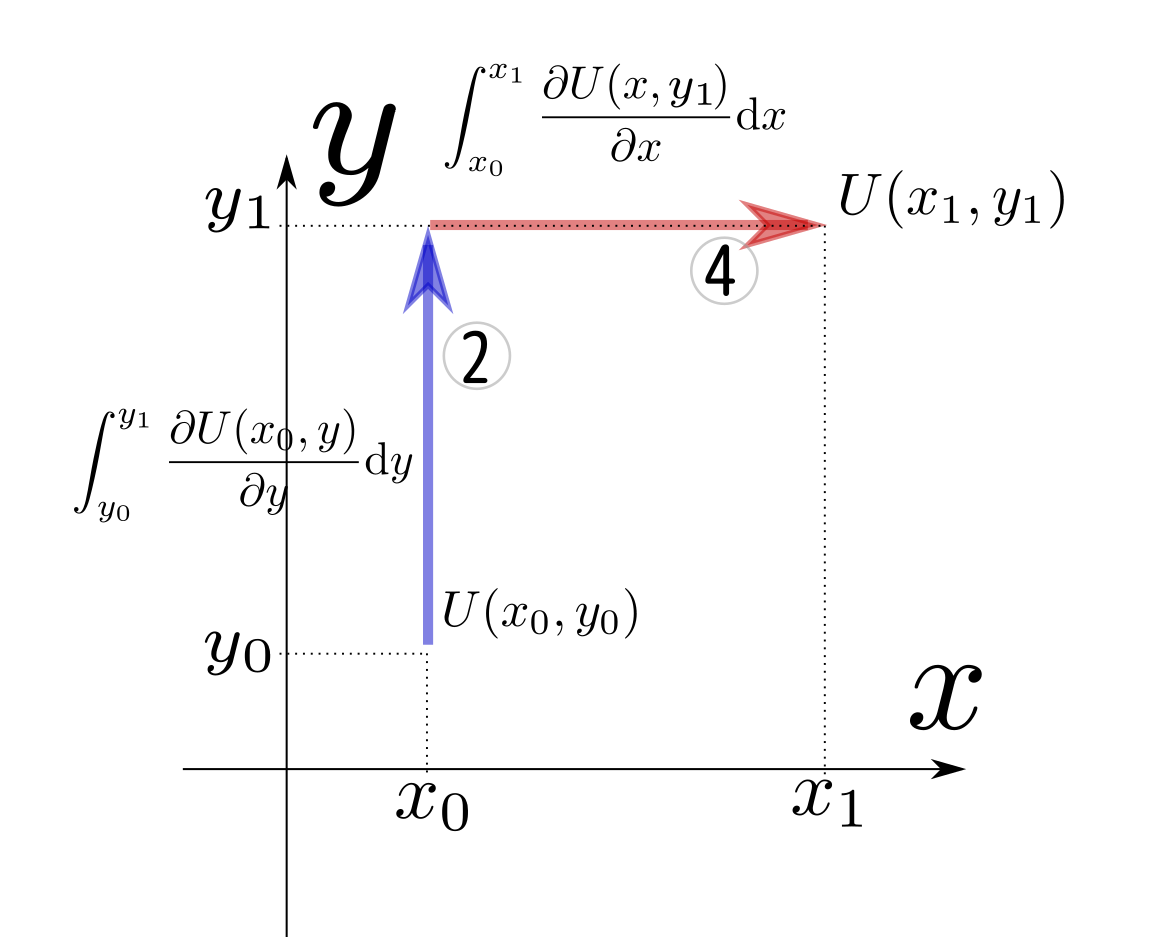
がある。
つまりは、北東に進むために「まず東、次に北」と進んでもよいし、「まず北、次に東」と進んでもよい、ということ。実は斜めに進む方法(そういう積分のやりかた)もちゃんとある。
このような積分は「線積分」と呼ばれる。
この二つの積分が一致するのか?というのが気になるところである。それはつまり、
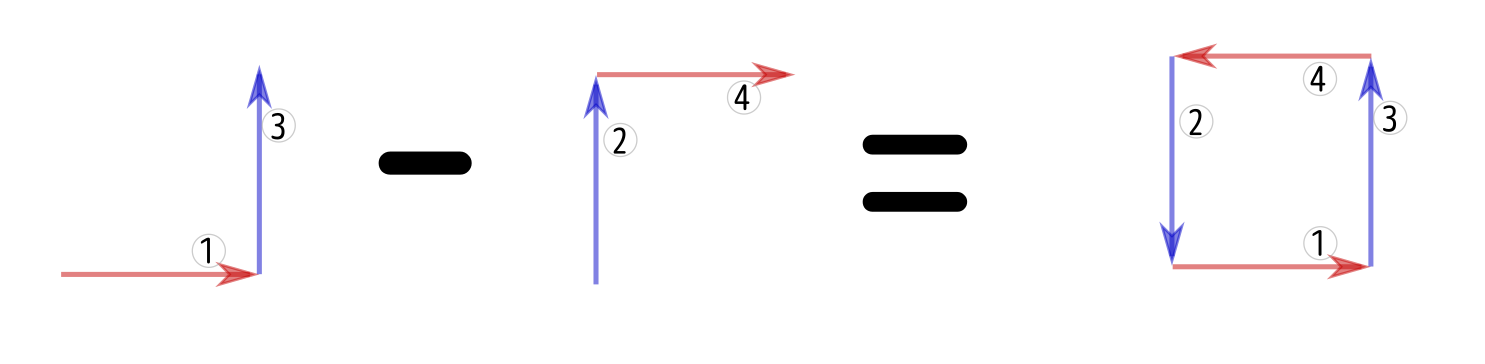
積分1+積分3 は 積分2+積分4 と一致するか?
という問題だが、これを少し変えると、
積分3ー積分2 は 積分4ー積分1 と一致するか?
という問題になる。そして、積分3ー積分2というのは、いわば積分3($y$微分)の$x$微分である。同様に積分4ー積分1は積分4($x$微分)の$y$微分であり、積分可能条件(あるいは、偏微分の交換)によればこの二つは等しい。
なお、これをさらに
積分1+積分3ー積分4ー積分2 は0か??
と読み替えると、これは「一周積分は0か?」を意味する。$U(x,y)$という関数が存在すれば、一周戻ってくれば$U(x,y)$も元の値に戻っている、ということを意味している。
これはベクトル解析で言う「rot」である。
これは位置エネルギーなどの「保存力の場」が満たすべき条件になっている