偏微分の注意その２

---

よくある誤り

　常微分の時に${\mathrm dz\over \mathrm dy}{\mathrm dy\over \mathrm dx}={\mathrm dz\over \mathrm dx}$ができたのだから偏微分でも${\partial {z}\over \partial y}{\partial {y}\over \partial x}={\partial {z}\over \partial x}$だろう。

---

　省略記法で書いているせいで「これでいい」と勘違いしてしまうことがある。誤解がないよう省略なしで書けば、常微分の${\mathrm dz\over \mathrm dy}{\mathrm dy\over \mathrm dx}={\mathrm dz\over \mathrm dx}$は${\mathrm dz({y})\over \mathrm dy}{\mathrm dy({x})\over \mathrm dx}={\mathrm dz(y({x}))\over \mathrm dx}$である一方、偏微分の${\partial {z}\over \partial y}{\partial {y}\over \partial x}\neq{\partial {z}\over \partial x}$（等式ではないことに注意）は $$\left({\partial {z({x},{y})}\over \partial y}\right)_{{x}}\left({\partial {y({z},{x})}\over \partial x}\right)_{{z}}\neq\left({\partial {z({x},{y})}\over \partial x}\right)_{{z}}$$ であり、本質的に違う計算である。常微分の方では三つの変数は「${x}$が決まると${y}$が決まり、次に${z}$が決まる」という関係であり、自由度は1しかない。つまり3変数の3次元空間の中である1次元的広がり（曲線）の上でしか運動できない。一方偏微分の方は「${x}$と${y}$が決まると${z}$が決まる（あるいはこの立場入れ替え）」という関係だから自由度2で、2次元的広がり（曲面）の上を動ける（だから偏微分は方向の指定が必要になるわけだ）。

---

　例として、${x}^2+{y}^2+{z}^2=R^2$が成り立つ、すなわち3次元の中の球面（2次元的広がり）の上に$({x},{y},{z})$がある）場合を考えよう。この場合${z}=\pm\sqrt{R^2-{x}^2-{y}^2}$とか${y}=\pm\sqrt{R^2-{x}^2-{z}^2}$のような関係式がある。複号があると考えるのが面倒なので、考える範囲を${x},{y},{z}$が全て正である領域に限ろう（複号は全て正をとる）。微分を実行すると、 $$\begin{equation} \left({\partial {z({x},{y})}\over \partial y}\right)_{{x}} =- {{y}\over \sqrt{R^2-{x}^2-{y}^2}},~~~~ \left({\partial {y({x},{z})}\over \partial x}\right)_{{z}} =- {{x}\over \sqrt{R^2-{x}^2-{z}^2}} \end{equation}$$ である。この二つの掛算をし、$\sqrt{R^2-{x}^2-{z}^2}={y}$であることを使うと、 $$\begin{equation} \left({\partial {z({x},{y})}\over \partial y}\right)_{{x}} \left({\partial {y({x},{z})}\over \partial x}\right)_{{z}} ={{y}\over \sqrt{R^2-{x}^2-{y}^2}}\times{{x}\over \sqrt{R^2-{x}^2-{z}^2}} ={{x} \over \sqrt{R^2-{x}^2-{y}^2}} \end{equation}$$ となる。一方、 $$\begin{equation} \left({\partial {z({x},{y})}\over \partial x}\right)_{{y}} =- {{x}\over \sqrt{R^2-{x}^2-{y}^2}} \end{equation}$$ だから、この二つの式から $$\begin{equation} \left({\partial {z({x},{y})}\over \partial y}\right)_{{x}} \left({\partial {y({x},{z})}\over \partial x}\right)_{{z}} = - \left({\partial {z({x},{y})}\over \partial x}\right)_{{y}}\label{henbibunminus} \end{equation}$$ という関係になっている（右辺のマイナス符号に注意！）。

　${x},{y},{z}$の間に適当な関係式（なんでもよい）を作り、その場合の$\left({\partial {z({x},{y})}\over \partial y}\right)_{{x}}\left({\partial {y({x},{z})}\over \partial x}\right)_{{z}} = - \left({\partial {z({x},{y})}\over \partial x}\right)_{{y}}$の両辺を別個に計算し、成立することを確認してみよう。

　この式は$z({x},{y})$などが微分可能である限り正しいことを以下で、二通りの方法で示そう。

　${x},{y},{z}$という3次元の空間を考えて、ある関係式（上の例では${x}^2+{y}^2+{z}^2=R^2$であった）があることによりこのうち二つが独立であったとする。関係があるのだから、三つの変数のうち一つを他の二つで表すことができる。そこで $$\begin{equation} {x}=X({y},{z}),~ {y}=Y({x},{z}),~ {z}=Z({x},{y}) \end{equation}$$ という三つの式を作ることができたものとしよう。第３の式に第２の式を代入すると、 $$\begin{equation} {z}=Z\left({x},Y({x},{z})\right)\label{zz} \end{equation}$$ という式ができる。計算の結果、この式は${z}={z}$という当たり前の式に戻る筈である。

---

　上の例の${z}=\pm\sqrt{R^2-{x}^2-{y}^2}$に${y}=\pm\sqrt{R^2-{x}^2-{z}^2}$を代入してみると、 $$\begin{equation} {z}=\pm\sqrt{R^2-{x}^2-(R^2-{x}^2-{z}^2)}=\pm\sqrt{{z}^2}\label{zzkekka} \end{equation}$$ となって、${z}={z}$になる（もともと複号は${z}$が正なら$+$、負なら$-$だったから、右辺は${z}$にしてよい）。

---

　つまり、この式の右辺は${x}$を含んでいるように見えるが、実は含んでいない（計算をすれば消えてしまう）。ここで、両辺を「${z}$を一定として${x}$で微分」する。計算するまでもなく（${z}$を一定としているのだから）左辺の微分は0である。一方右辺は${x}$が２箇所にあることから微分の結果は二つの式の和となり、結果が0となる（二つの項が打ち消す）。すなわち、

$$\begin{equation} 0=\overbrace{\left( {\partial {Z({x},Y)}\over \partial x}\right)_{Y}}^{左の{x}を微分} +\overbrace{\left( {\partial {Z({x},Y)}\over \partial Y}\right)_{{x}}\left( {\partial {Y({x},{z})}\over \partial x}\right)_{{z}}}^{右の{x}を微分} \end{equation}$$ が導かれる。

　どんなものでもよいので${x},{y},{z}$の関係式${z}=Z({x},{y})$を作って、これから${y}=Y({x},{z})$を求めたうえで、上の$Z({x},Y({x},{z}))$にあたる式をつくり、その式を（簡略化せずにそのまま）${z}$で微分すれば1となり、${x}$で微分すれば0となることを確認せよ。

　以上は計算による導出だが、次に図解を試みよう。変数の間の関係式を成立させつつ、

1. ${x}$を一定として${y}$を変化（連動して${z}$も変化）。
2. ${y}$を一定として${z}$を変化（連動して${x}$も変化）。
3. ${z}$を一定として${x}$を変化（連動して${y}$も変化）。

という三つの変化を起こして元の場所に戻ってくる経路を考える。

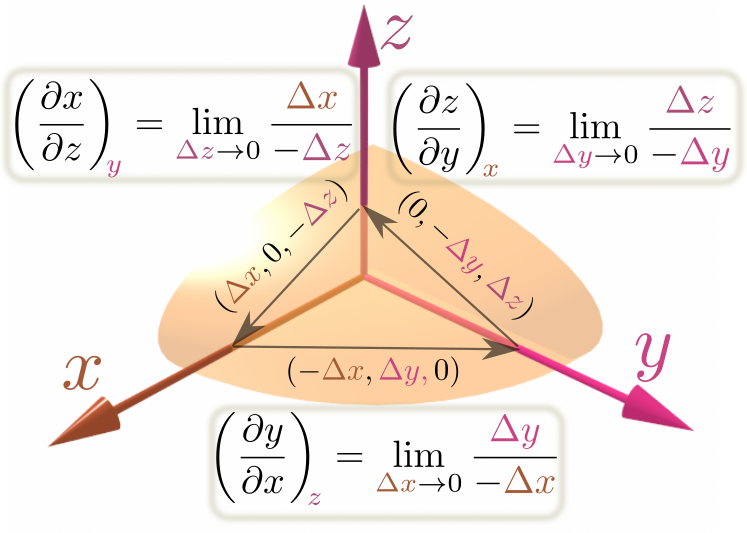
　それぞれの過程において図に描き込んだような分数を計算し、その掛算を行うと、 $$\begin{equation} {{\Delta y}\over -{\Delta z}}\times {{\Delta z}\over -{\Delta x}}\times {{\Delta x}\over -{\Delta y}}=-1 \end{equation}$$ となる（分母分子に同じものが２回ずつ現れ、分母にマイナスが３回現れる）。極限を取ればこれは $$\begin{equation} \left({\partial {y({x},{z})}\over \partial x}\right)_{{z}}\times \left({\partial {z({x},{y})}\over \partial y}\right)_{{x}}\times \left({\partial {x({y},{z})}\over \partial z}\right)_{{y}}=-1 \end{equation}$$ になる。$\left({\partial {x({y},{z})}\over \partial z}\right)_{{y}}={1\over \left({\partial {z({x},{y})}\over \partial x}\right)_{{y}} }$であるこの場合は、同じ変数${y}$を固定しての微分だから、逆数になってよい。。