青字は受講者からの声、赤字は前野よりの返答です。
腹が減って集中できないので次から朝飯をちゃんと、食べてきます。
朝から腹減らしてはいけませんな。
至近距離に行ってできるだけ単純に関数をみるのは自然科学では大切なのかもしれないと、若干悟った。simple is best!
はい、それは大切な考え方です。
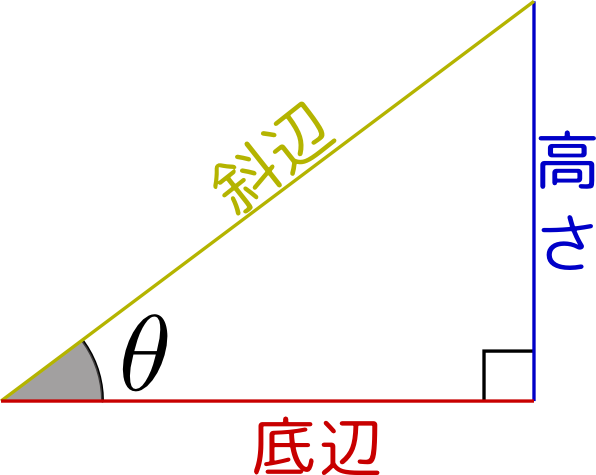
高校で習った${\sin\pi\over\pi}=1$と$\sin\theta=\theta(\theta\ll 1)$は近いのか? 微分が極限で習った範囲だから$x\ll1$になると思うし。弧度法を使わずに木星の距離を求めることができるのか?
$\lim_{\theta\to0}{\sin\theta\over\theta}=1$のことかな? これはもちろん、$\sin\theta=\theta$と同じ式です。弧度法じゃなくても計算が少しだけややこしくなるだけで、三角関数を作ることも距離を計算することもできますよ。
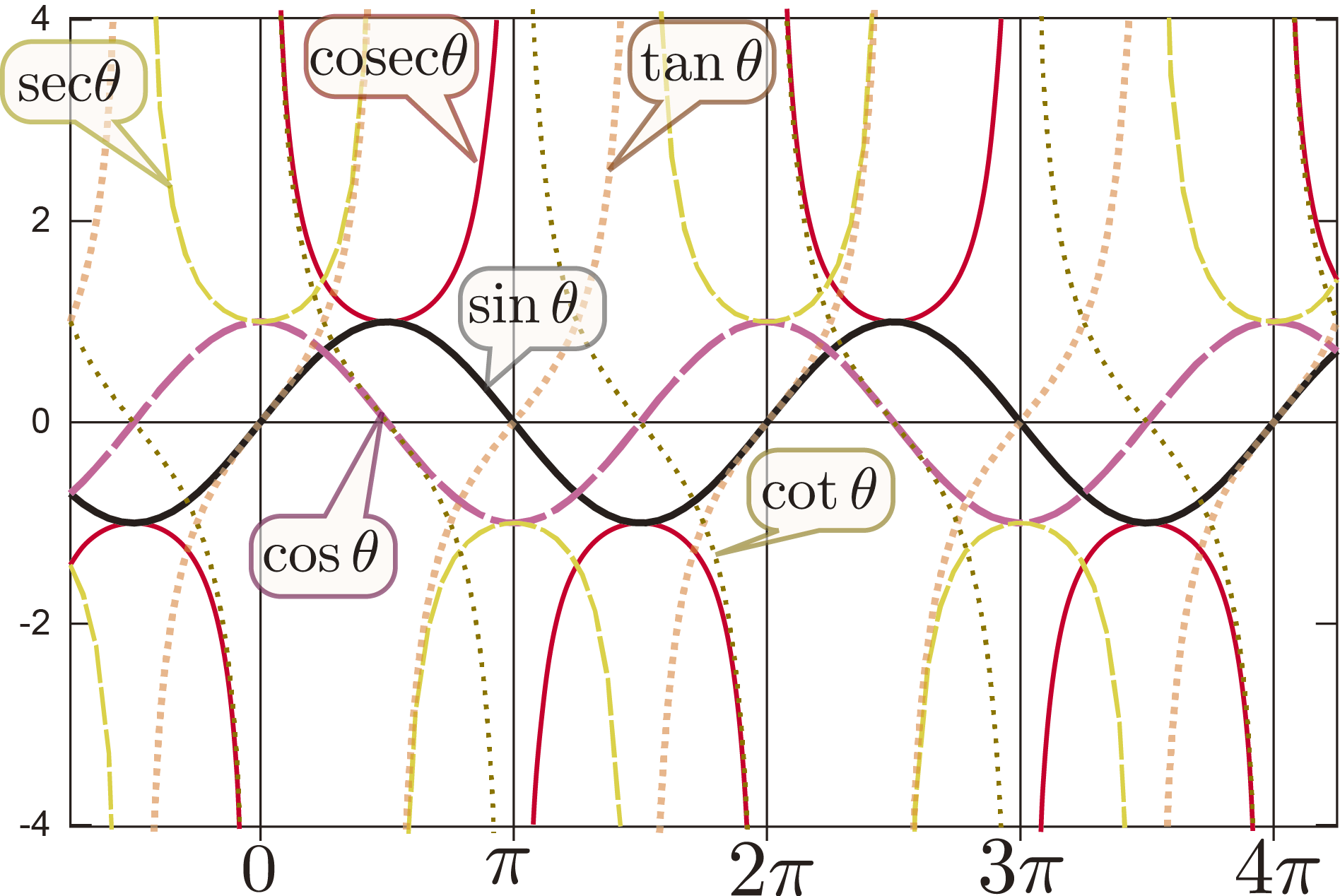
$\sin\theta$の$\theta$が限りなく小さいとき、$\sin\theta\fallingdotseq0$なのは知っていましたが、$\sin\theta\fallingdotseq\theta$なのは知らなかったので、面白かったです。$\sec\theta$や$\cot\theta$は初めて習ったので、これから慣れていこうと思います。
$\sin\theta\fallingdotseq\theta$は後でも出てきます。
$\theta\ll1$のとき$\sin\theta\fallingdotseq\theta$は知っていたが、$\cos\theta\fallingdotseq1-{\theta^2\over2}$は初めて知り、また確かに$\sin^2\theta+\cos^2\theta$に代入したとき1に近似していてなるほどと思った。
関数を近似する、という考え方を理解していきましょう。
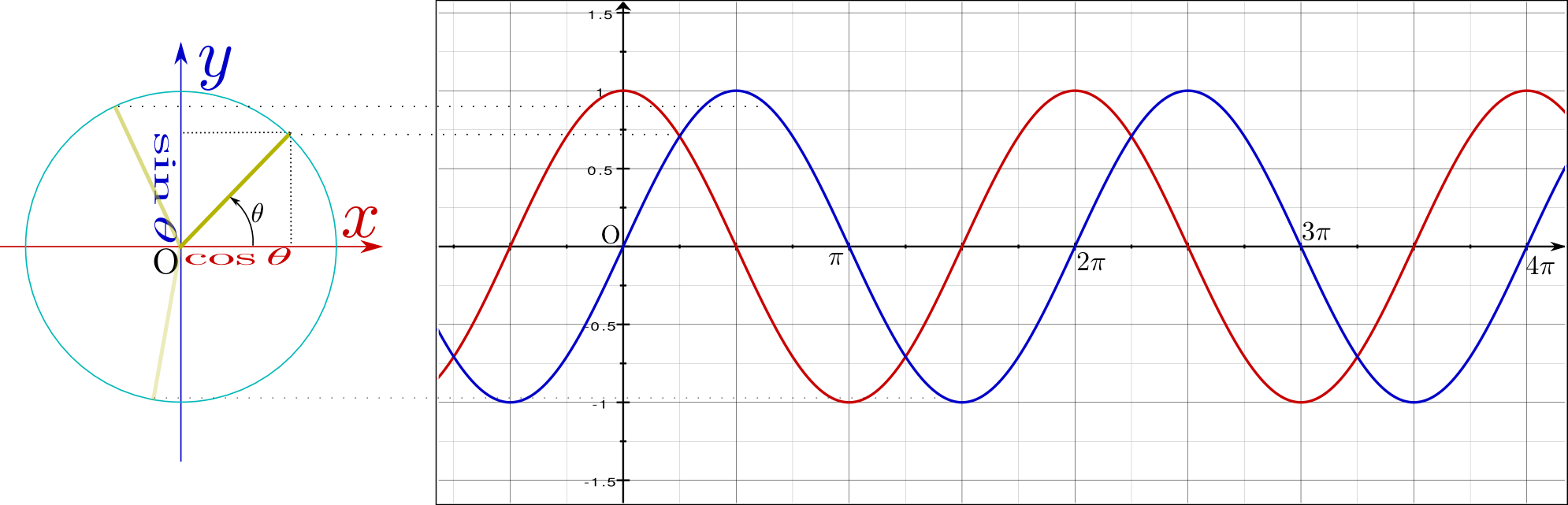
cosとsinのグラフが対応しているのがわかった。また、cosec,sec,cotを学べてよかった。今まで苦労して覚えた公式が別で表すことができてすごいと思った。
言うてはなんですが苦労して覚えてはいけなかったのです。
なんとなくでやってきた三角関数の公式をただ暗記していたので、こんかいの授業で絵をイメージしたのでいい勉強になりました。この授業では、まったく新しい(高校では習わない内容)しますか?
絵のイメージは大事に。最後の方で微分方程式というのをやります。
いい復習になった。楽しかった。
それはよかった。
三角関数を今までと違った視点でとらえると公式の意味がわかり、理解度が深まりました。
いろんな視点から物を見ていきましょう。
三角関数ってこんな奥が深いなと感じました。
まぁそういうこと言うとどんな関数は奥は深い。
三角関数の公式だけでなく原理をあらためて理解できた。
公式なんてどうでもよい(そんなものは本を見ればよい)から、まず原理。
三角関数をさらに勉強することで、三角形の色々な関係がわかって、新しい発見が多く興味深い授業でした。
三角関数はこれからもいろんなところで使います。
公式を覚えるのではなく意味を理解することができたのでとても勉強になりました。
意味がいちばん大事ですよ。
微小なsinθやcosθの性質がわかった。
それはよかった。
sinθやcosθの関係がわかった。
それはよかった。
三角関数の公式の意味が分かってよかったです。
意味がわかることが、第一歩。
図を見て考えれば、憶えなくても良い公式、やらなくても良い計算が見つかる。暗記ではなく、理解していきたい。
図解していくことでいろんなものがつながります。
${1\over\cos\theta}=\sec\theta,{1\over\sin\theta}={\rm cosec}~\theta$という新しい言葉をならった。$\sin\theta\fallingdotseq\theta,\cos\theta\fallingdotseq1-{\theta^2\over2}(\theta\ll1)$よく物理で使われている定義のしくみが分かって面白かった。
このあたりは関連付けて理解していきましょう。
三角関数の近似の仕組みがわかった。$\cos\theta=1-{\theta^2\over2}$になっていることが実際にやってみてわかった。
この近似の考え方はとても大事です。
数学の授業だけど「自然科学のための」数学なだけあって、物理の話にもつながっていてとてもおもしろかった。ずっと何年もやってきたおなじみの三角関数のはずなのに、いろんなことを拡張したら身近なものに応用できまくることに気づいてなかった。
自然科学にとっては数学は「使うためにある」ものなので、常に使い途は考えていきましょう。
三角関数の定義を改めて確認でき、また図を書くことの重要性を再認識できた。
三角関数は特に図形と結びついてますから、図は大事です。
三角関数の近似値を真面目に計算したのは初めてだった。
電卓叩きながらいろいろ遊んでみてください。
風邪が一週間治らないです。どうしましょう?
こんなとこに相談書いている場合じゃない。医者に行こう。でなかったら栄養たくさん取ってしっかり寝る。
今までは公式を覚えることに必死だったけど図の関係を覚えれば公式を忘れていても大丈夫だとわかったので、図の関係をしっかり理解するようにしたい。
まずは「意味を理解する」ことですよ。
電卓で計算することによって、公式があたっているのを実際に確かめて理解が深まった。
実際に数字で計算することも大事ですね。
三角関数のsinθ、cosθ、tanθの関係性がsin0.1やcos0.1のときの計算でも活用することを知ることができた。
一般的な関係式はいろんな局面で使わるわけです。
弧度法の定義であいまいだったところの理解が深まった。三角関数の定義が拡大された理由が納得してなかったけど、今日の説明聞いてスッキリしました。
スッキリ理解していきましょう。
高校で習った$\tan^2\theta+1={1\over\cos^2\theta}$とかの式の意味がわかってよかったです!!
意味がわからないのでは「習った」とは言えないよ。
三角関数が高さを測ったり距離を調べたりすることなど実用的に使われていることを初めて知ったので面白いなと思った。
もちろん、使い処があるからこそ、勉強しているわけです。
$\sin^2\theta+\cos^2\theta=1$より$\theta^2+\left(1-{\theta^2\over2}\right)^2\fallingdotseq1$となることにびっくりした。面白いと思った。
成立すべき式は、近似しても成立するものなのです。
三角関数についてよくわかった。
それはよかった。
何となくわかっている事だけだったので、大丈夫。
「何となく」じゃちっとも「大丈夫」とは言えないのだけど。
月までの距離など、数学を自然科学にどんな風に使うのかの具体例があってわかりやすかったです。
具体性あってこその数学です。
知識確認ができました。
それはよかった。
脳内のイメージを視覚的にとらえることができた。この利点はコンピュータ授業の最大の長所だと思いました。
図を自分で動かしてみることで理解が進みますね。
図を書きながらだったので分かりやすかった。
図を自分で書くのは大事です。
三角関数、新たにcosec,sec,cotを憶えた。sin 0.1,sin0.01,sin0.001の数字が似ていた。
「なぜ数字が似てくるのか?」ということにもちゃんと答があります。
三角関数の基本的なしくみがよくわかった。
それはよかった。
高校でもならう三角関数の公式をていねいに解説していて面白かったです。
よく理解しておいてください。
三角関数のしくみ?みたいなものがわかった。図で覚えると楽!!
三角関数は特に、図は大事です。
今までただの公式として覚えていた三角関数の定義が、仕組みを知るだけで簡単に理解できた。
最初は仕組みを知る処から行かないとダメですよ。
三角関数において$\theta\ll1$にすると1次関数、2次関数の式とほぼ近い形になった!! これを数式的に証明したらどうなるか気になる…。tanθ,secθ、cotθにも色々秘密があるかもしれない。ヒマな時計算機をぽちぽちしようかな。
ぜひやってみてください。いろいろ発見があるはず。
前回前々回の次数の考えが三角関数でも使えることがわかって驚きました。
どんな関数も「近所」だけをみることで簡単になるものなのです。
$\sin\theta\fallingdotseq\theta$はなぜそうなるかなどなくただ覚えていたようなことになっていたので、あらためて思い出せてよかったです。
これは覚えることじゃなくて、図とともに理解しておくことですね。
三角関数の基礎。$\cos\theta\fallingdotseq1-{\theta^2\over2}$がなぜこのような形になるかの理由が少しわかった。
「少し」か。まぁおいおい、完璧にわかってください。
三角関数のθが0に近づいたときに、sinθとcosθの面白い関係が見えてきました。斜辺を1とした時の三角関数の関係と、底辺、高さをそれぞれ1とした時の関係は一緒でも新しい考えが生まれてきました。考え方をしっかりおさえて、いつでも三角関数の関係がわかるようにしておきます。
三角関数の相互関係は、これからもよく使います。
sin0.1やcos0.1など数が小さいときは、その値が1に近づくことがわかった。
1に近づくのはcosのことかな?それともθとsinθの比のことかな?
今日は、風邪気味で何度も先生の威圧感に負けそうになったが、初めて聞く言葉についてに負けた…。
負けちゃダメだろう。
三角関数は図で理解します。今日は高校で公式として覚えた式の原理を納得することができました。
図で理解は大事ですよ。
高校の三角関数の延長みたいに感じた。次の合成関数は難しそうなので頑張りたい。
今日の話はほぼ高校レベルです。少しずつ大学数学になってきますが、次もまだ高校レベルかも。
三角関数をやった! secθやcosecθ、cotθなど新しい三角関数が三つもあって、高校のときとつながってなるほどと思いました。
まとめて理解しておいてください。
三角関数の性質について理解が深まった。$\cos\theta\fallingdotseq1-{\theta^2\over2}$を理解するのはちょっと難しかった。
あの式は結構大事(また出てくる)。
三角関数の復習ができたのでよかったです。また、教科書が改めて素晴らしいと思いました。
それはどうも。しっかり復習しておきましょう。
改めて三角関数について詳しく学べました。しっかりと復習したいです。
じっくり理解しておきましょう。
三角関数の公式はいままでは暗記しようとしていたが、絵で覚えた方が分かりやすかった。
暗記してすますような勉強はしてはいけません。
三角関数が楽しかったです。
それはよかった。
三角関数の性質について関数の形をみながら終えたのが楽しかった。
イメージをつかんでおきましょう。
cosθやsinθの小数点以下を少しずつずらして出てくる変化に感動した。
どうしてああなるか、がわかるあたりも面白いですよ。
θが小さいときのsin,cosが分かった。新たな記号も出てきたので覚えたい。
また後でも関係してくるので、近似式のところは理解しておきましょう。

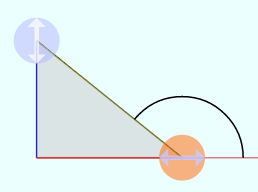 のようにθが直角より大きくなり「
のようにθが直角より大きくなり「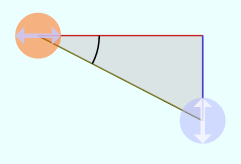 のようにθが負になり「
のようにθが負になり「 から
から に向かう方向が「上」「右」の時にsin,cosは正であり、「下」「左」の時にはsin,cosは負である。図ではそれを
に向かう方向が「上」「右」の時にsin,cosは正であり、「下」「左」の時にはsin,cosは負である。図ではそれを や
や が鏡文字になることで表現している。
が鏡文字になることで表現している。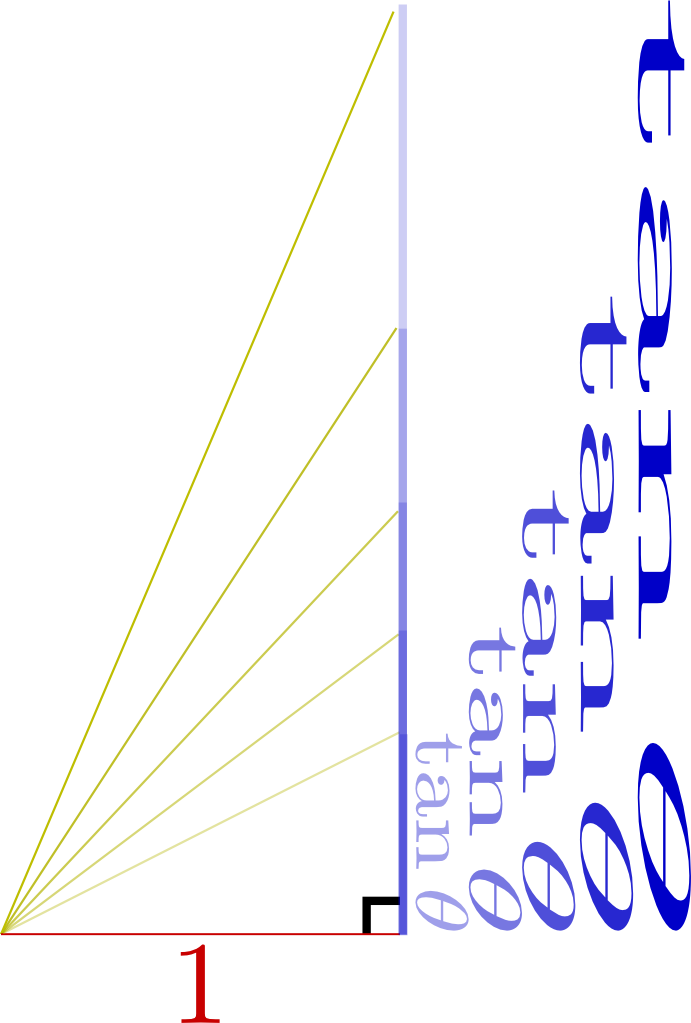

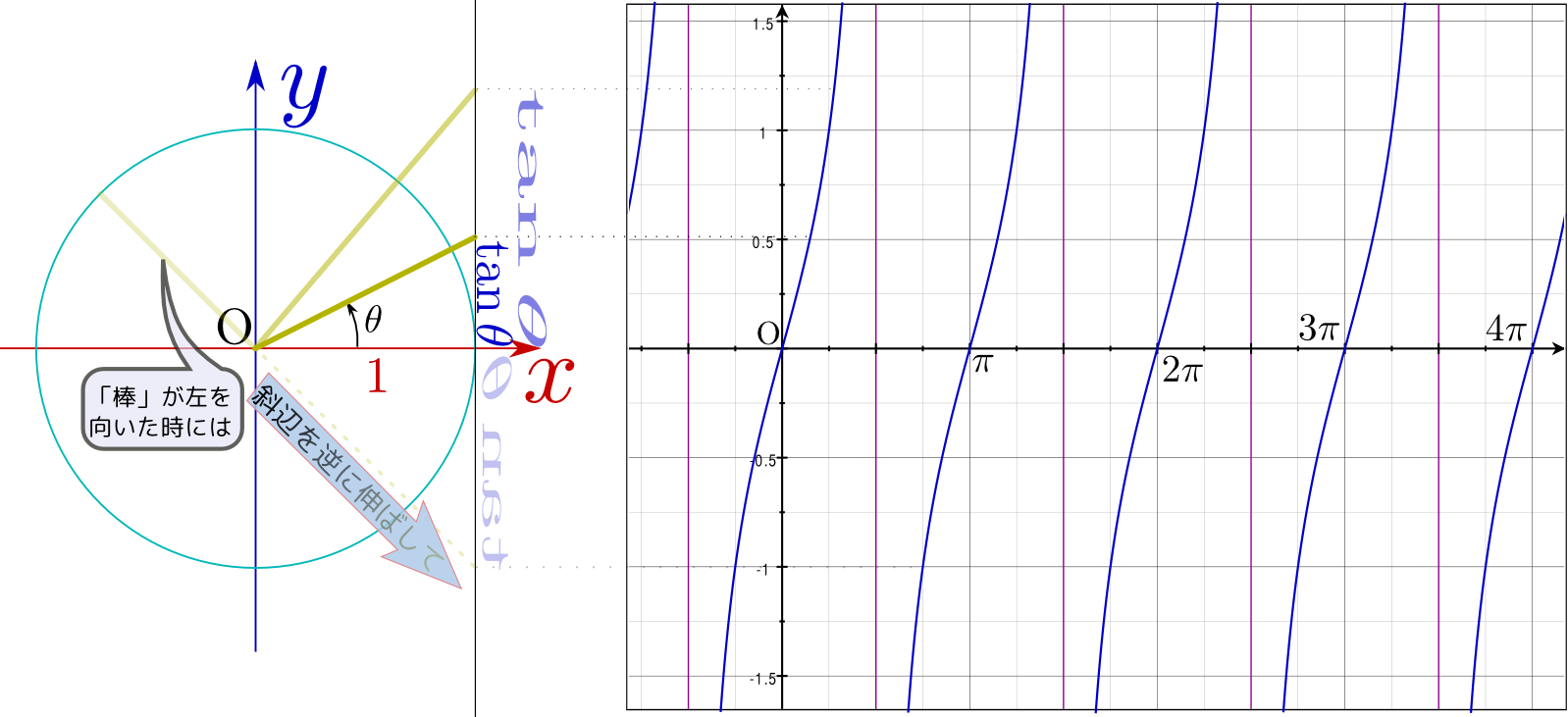
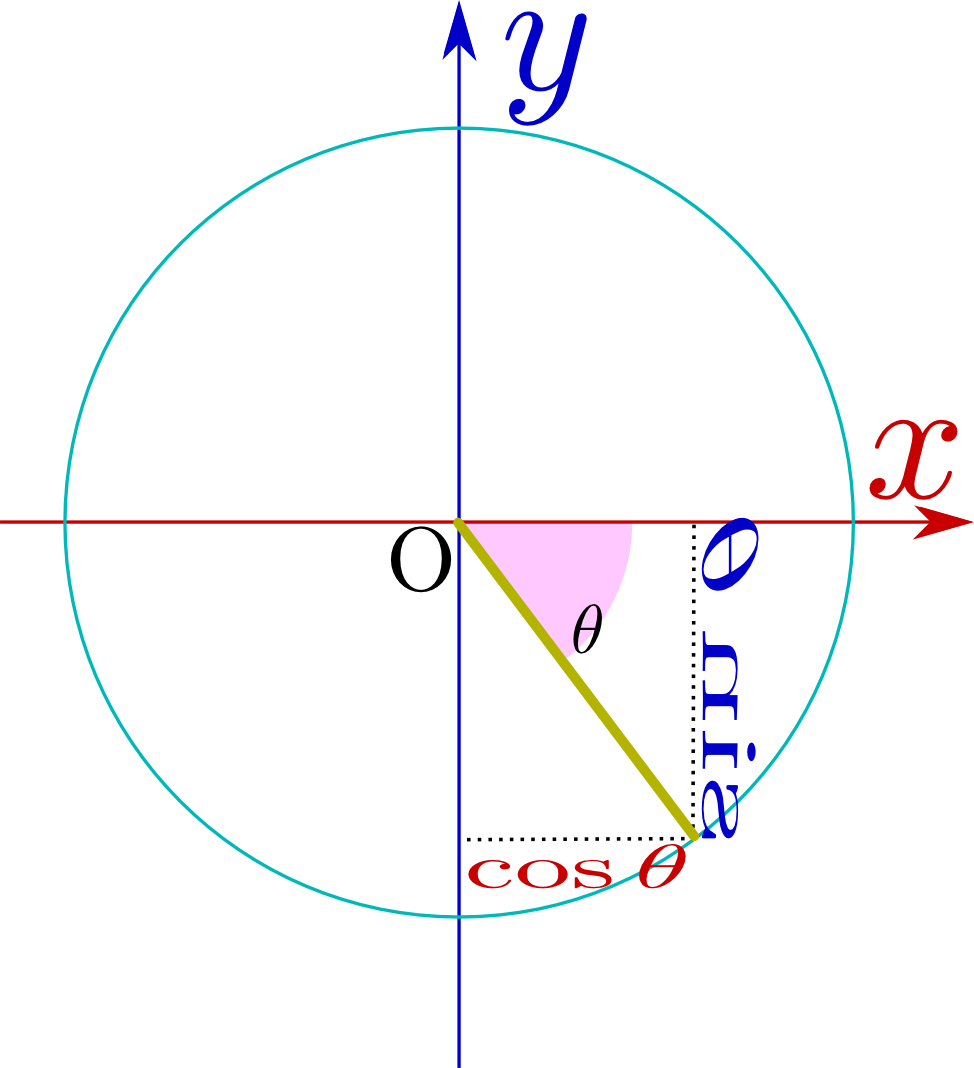
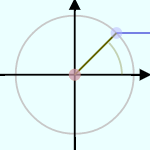 は半径1の円(単位円)を描いたもので、中心から円周の一点に向かっている棒
は半径1の円(単位円)を描いたもので、中心から円周の一点に向かっている棒 の角度に応じて、
の角度に応じて、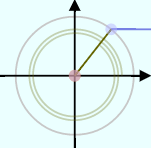 のように2πより大きい(何周も回る)角度にしたり、
のように2πより大きい(何周も回る)角度にしたり、 のように負の角度にしたりもできるので、いろいろ変えて状況を確認して欲しい。
のように負の角度にしたりもできるので、いろいろ変えて状況を確認して欲しい。
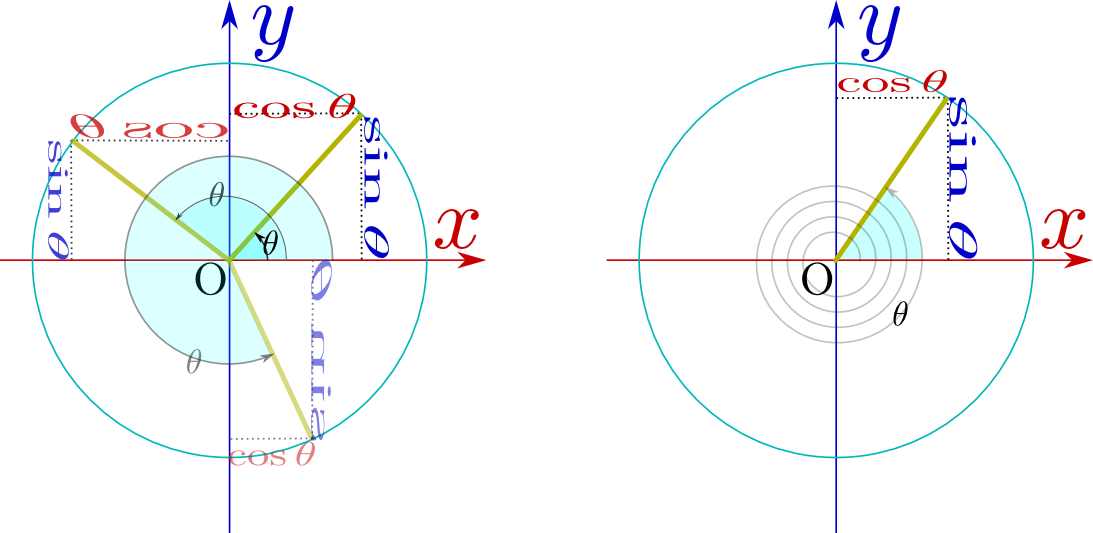
 の部分の薄い色になっている
の部分の薄い色になっている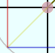 の方が、θよりπラジアン(180度)大きい角度の場合の「長さ1の棒」になっている。sin,cosがπ足されることでどう変化するかを、図から読み取っていけば、公式が作られる(この公式は式として覚えようとしなくても、意味を考えればすぐにわかる)。
の方が、θよりπラジアン(180度)大きい角度の場合の「長さ1の棒」になっている。sin,cosがπ足されることでどう変化するかを、図から読み取っていけば、公式が作られる(この公式は式として覚えようとしなくても、意味を考えればすぐにわかる)。