自然科学のための数学2015年度第30講

偏微分方程式

　ここまで考えた微分方程式は常微分$\left({\mathrm d\over\mathrm dx},{\mathrm d\over\mathrm dt},\cdots\right)$を用いた微分方程式だったが、偏微分$\left({\partial\over \partial x},{\partial \over\partial y},{\partial\over \partial t},\cdots\right)$を用いた微分方程式もある。

　常微分方程式の場合、積分していくことで解が求められた。この時積分定数という形で解に未定のパラメータが入った。たとえば常微分方程式${\mathrm d\over\mathrm dx} f({x})={x}$の解は$f({x})={{x}^2\over 2}+C$である。これに似た偏微分方程式 \begin{equation} {\partial\over \partial x}f({x},{y})={x} \end{equation} の解は$f({x},{y})={{x}^2\over 2}+C({y})$である。

　常微分方程式なら独立変数（たとえば${x}$）の積分により解が出たから、${x}$によらない積分定数として解に現れた。$({x},{y})$の二つの独立変数を持つ偏微分方程式では${x}$の積分によって現れた積分定数は${y}$の関数であってよい（逆に${y}$の積分による積分定数は${x}$の関数であってよい）。

　「微分して0$\Rightarrow$定数」ではないことが偏微分方程式の注意点である。

　もう少しだけ複雑な例、 \begin{equation} \left({\partial\over \partial x}+a{\partial\over \partial y}\right)f({x},{y})=0 \end{equation} を考えよう。これの解の一つが$a{x}-{y}$であることはすぐに確認できるが、実は$F$を任意の1変数関数として、その引数に$a{x}-{y}$が代入された$F(a{x}-{y})$も解になる。というのは$F(a{x}-{y})$を、「${y}$を一定にして${x}$で偏微分」したものと「${x}$を一定にして${y}$で偏微分したもの」は$-a$倍違うから、 \begin{equation} \left({\partial\over \partial x}+a{\partial\over \partial y}\right)F(a{x}-{y})=0 \end{equation} が成立するからである。たとえば$\tan(a{x}-{y})$でも$\log(a{x}-{y})$でも、あるいは${(a{x}-{y})^5\over \sqrt{\sin(a{x}-{y})}}$のような複雑な関数でも、この偏微分方程式の解となる\footnote{分母が0になったりルート内が負になったりする領域が省かれるのはもちろんである。}。このような変数の組み合わせを見つけるというのも偏微分方程式の解き方である。

偏微分方程式の解き方

　ここでは、求めるべき関数を$f({x},{y})$のように二つの独立な変数${x},{y}$によって決まる2変数関数として説明する。変数が${t}$になったり${r}$になったりしても考え方は変わらないし、3変数、4変数と変数の数が増えても、基本的には同様の手順で解いていく。

変数分離による解法

\begin{equation} \left({\partial\over \partial x},{\partial\over \partial y}を含む微分演算子\right)f({x},{y})=g({x},{y}) \end{equation} のような微分方程式が与えられた時、これの解をいきなり探すのは難しい。そこで、この方程式の解が$f({x},{y})=X({x})Y({y})$のように${x}$を変数とする部分と${y}$を変数とする部分の積になるだろう、と仮定してみる。その後計算した結果、 \begin{equation} \left({\partial\over \partial x}と{x},X({x})の式\right) = \left({\partial\over \partial y}と{y},Y({y})の式\right) \end{equation} のように左辺と右辺に${x}$と${y}$が分離できたとする（これを「変数分離」と呼ぶ）。この式が成立するためには左辺も右辺も定数にならなくてはいけない\footnote{${x}$と${y}$は独立変数で、勝手に変化できるのだから、左辺が${x}$によって変化し、右辺が${y}$によって変化したら、この式は運がいい時にしか成立しない式になる。}ので、その定数を$\alpha$と置いて、 \begin{equation} \left({\partial\over \partial x}と{x},X({x})の式\right)=\alpha,~~ \left({\partial\over \partial y}と{y},Y({y})の式\right)=\alpha \end{equation} という常微分方程式二つを解けばよい、というのが「偏微分方程式の変数分離」である。なお、変数分離で答が求まるというのはあくまで「仮定」であるから、これで正しい解が出ているかどうかについては注意しなくてはいけない。

　$\alpha$は任意の定数だから、その定数に応じてたくさんの解が出るが、境界条件などにより実際の解がどのようになるかが決められる（このあたりは常微分方程式でもあったこと）。

「微分演算子の因数分解」による解法

　常微分方程式の時に、「微分演算子の因数分解」を行って解く方法があったことを思い出そう。同様にもし我々がたとえば偏微分方程式の微分演算子を \begin{equation} \left( \left({\partial\over \partial x}\right)^2 +(a+b){\partial^2\over \partial x\partial y} +ab\left({\partial\over \partial y}\right)^2 \right)f({x},{y}) =\left({\partial\over \partial x}+a{\partial\over \partial y}\right)\left({\partial\over \partial x}+b{\partial\over \partial y}\right)f({x},{y})=0 \end{equation} のように`因数分解'して \begin{equation} \left({\partial\over \partial x}+a{\partial\over \partial y}\right) f({x},{y})=0 ~~または~~ \left({\partial\over \partial x}+b{\partial\over \partial y}\right)f({x},{y})=0\label{delfactoring} \end{equation} のように式を分離することができれば、問題を簡単化（二階微分方程式が一階微分方程式になった！）できる。

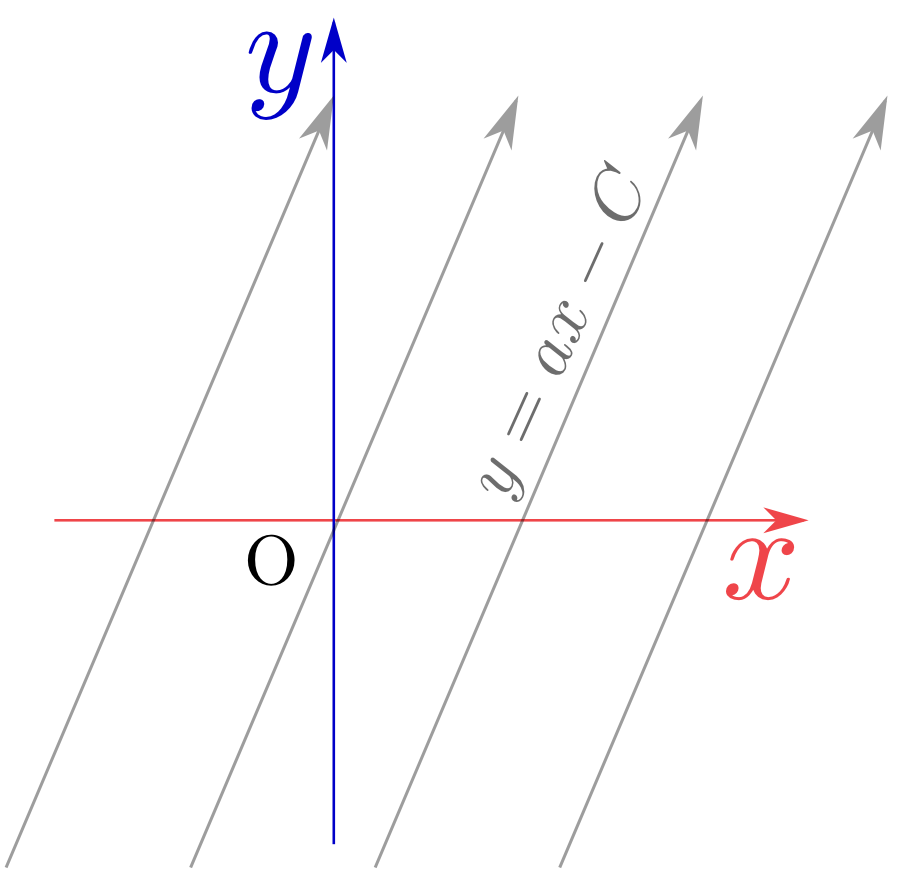
　上の場合、第１の式の解は（任意の関数を$F$として）$F(a{x}-{y})$であり、同様にもう一つの解は（やはり任意の関数を$G$として）$G(b{x}-{y})$である。一般解は、$F(a{x}-{y})+G(b{x}-{y})$となる。

　$F(a{x}-{y})$という関数は、$a{x}-{y}=C$（$C$は定数）を満たす場所（つまり直線${y}=a{x}-C$上）では一定である。上で求めた解は、「直線${y}=a{x}-C$上で一定になる関数」と「直線${y}=b{x}-C'$上で一定になる関数」の和だということになる。

　上の場合「直線」の上で解となる関数が一定となったが、 \begin{equation} \left( P({x},{y}){\partial\over \partial x} + Q({x},{y}){\partial\over \partial y} \right)f({x},{y})=0 \end{equation} のような偏微分方程式の場合、解である関数$G({x},{y})$を一つ見つけることができたなら、任意の関数$F(t)$の$t$に$G({x},{y})$を代入した$F(G({x},{y}))$もやはり解となる。この場合は、$G({x},{y})=C$(定数)であるような線（直線とは限らない）の上で$F$は一定となる。

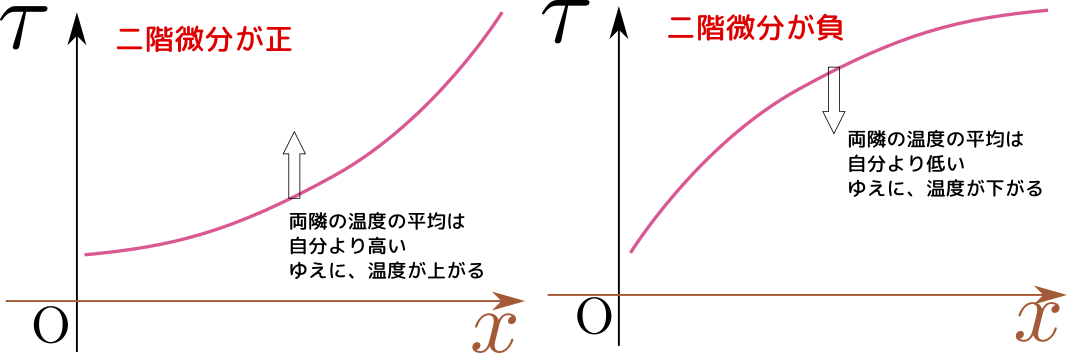
　微分方程式 \begin{equation} \left({\partial\over \partial x}+2{x}{\partial\over \partial y}\right)F({x},{y})=0\label{tokuseihoubutsu} \end{equation} は特性曲線が文字通り曲線になる例である。この微分方程式は一つの解として${y}-{x}^2$を持つ（代入して確認せよ）。よって、$f$は任意の微分可能な関数とすれば、 \begin{equation} F({x},{y})=f({y}-{x}^2) \end{equation} が解となる。${y}-{x}^2=(定数)$を満たす線（${x}=0$を軸とする放物線になる）の上で一定であるような関数なら全て解になる。

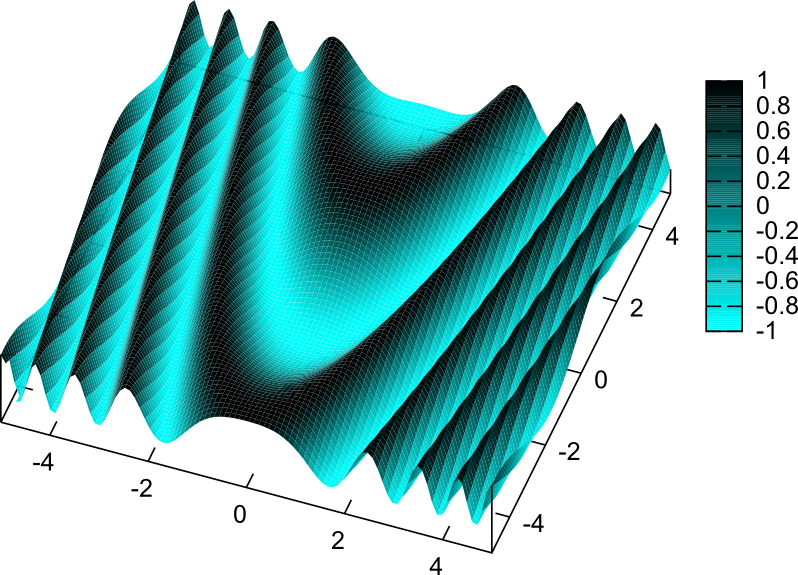
　上の図は、$\sin({y}-{x}^2)$の3Dグラフである（放物線の上で一定になるような関数になっている）。

　このような線（上の例では放物線）を「特性曲線(characteristic curve)」と呼ぶ。特性曲線を求めるということも、偏微分方程式の解法と言える。

　「どんな関数でもよい」と言われると「解が求まってない」と心配になるかもしれないが、それは境界条件を指定していないからである。偏微分方程式も常微分方程式と同様に、方程式だけからは決まらないパラメータがあり、それを指定する必要がある。このあたりは以下でやる実例のところで説明しよう。

　もう一つの例として、 \begin{equation} \left( {x}{\partial\over \partial y} -{y}{\partial\over \partial x} \right)f({x},{y})=0\label{tokuseien} \end{equation} を考えてみよう。今度は$({y},-{x})$という方向への微分が0ということである。この微分方程式の図形的意味から$\theta$方向に移動しても変化しない（特性曲線が円）という意味であることがわかるから、解は$f({x},{y})=F(r({x},{y}))$である（$r({x},{y})$はもちろん極座標の$r$で$r({x},{y})=\sqrt{{x}^2+{y}^2}$という関係）。この解の偏微分係数を求めてみると \begin{equation} {\partial\over \partial x}F(r({x},{y}))=\underbrace{{\partial {r}\over \partial x}}_{{{x}\over r({x},{y})}}{\mathrm d \over \mathrm dr}F(r),~~~ {\partial\over \partial y}F(r({x},{y}))=\underbrace{{\partial {r}\over \partial y}}_{{{y}\over r({x},{y})}}{\mathrm d \over \mathrm dr}F(r) \end{equation} となり、${x}{\partial \over \partial y}F-{y}{\partial \over \partial x}F$という計算をすると0になることがわかる。

　実はこの計算は（図形的意味が「${\theta}$方向に移動しても変化しない」だったことからもわかるように）、 \begin{equation} \left( {\partial\over \partial\theta}f(x({r},{\theta}),y({r},{\theta})) \right)_{{r}} = \underbrace{ \left({\partial {y({r},{\theta})}\over \partial \theta}\right)_{{r}}}_{{x}} \left({\partial {f}({x},{y})\over \partial y}\right)_{{x}} + \underbrace{ \left({\partial {x({r},{\theta})}\over \partial \theta}\right)_{{r}}}_{-{y}} \left({\partial {f({x},{y})}\over \partial x}\right)_{{y}} \end{equation} と表すこともできる。以上のことを一般化して、以下のことが言える。 \begin{equation} \left( P({x},{y}){\partial\over \partial x} + Q({x},{y}){\partial\over \partial y} \right)f({x},{y})=0\label{PdelQdel} \end{equation} のような形の微分方程式があったとき、 \begin{equation} \lambda({x},{y}) P({x},{y})={\partial {x({x},{y})}\over \partial X},~~~ \lambda({x},{y}) Q({x},{y})={\partial {y({x},{y})}\over \partial X}\label{PQlambdadel} \end{equation} となるような座標変換$({x},{y})\to({X},{Y})$を見つけることができたなら、この方程式に$\lambda({x},{y})$を掛けてから、見つけた式を使うことで、 \begin{equation} {\partial \over \partial X}f(x({X},{Y}),y({X},{Y}))= \left( {\partial {x({x},{y})}\over \partial X}{\partial \over \partial x} +{\partial {y({x},{y})}\over \partial X}{\partial \over \partial y} \right)f({x},{y}) =0 \end{equation} を得る。$f(x({X},{Y}),y({X},{Y}))$が${X}$を含まぬ${Y}$だけの関数が微分方程式の解となる。

　「偏微分には方向がある」とここまで（少々くどく）述べたが、今日述べた微分方程式の解き方は「偏微分が0になる方向を探す」という方針の解き方である。

以下で具体的な偏微分方程式の例を述べよう。

熱伝導方程式

熱伝導方程式

　次の微分方程式は、1次元的な物体（細い棒など、断面積が無視できるような物体）の温度を表す関数の満たす微分方程式である。$\tau({t},{x})$は時刻${t}$、場所${x}$における温度を表す$\tau$はギリシャ文字の t に対応する文字で、読み方は「タウ」。温度(temperature)だから$t$を使いたいところだが、$t$は時間に使っているし、$T$も別の意味で使うのでギリシャ文字に登場願う。。

\begin{equation} \left({\partial \tau({t},{x})\over \partial t}\right)_{{x}} =K\left({\partial^2 \tau({t},{x})\over \partial x^2}\right)_{{t}} \end{equation}

　この式にはどんな意味があるのかを図解しておこう。右辺は${x}$に関する二階微分、すなわち${t}$を一定として考えると、${x}$-$\tau$グラフの曲がり具合であり、$\left({\partial^2 \tau({t},{x})\over \partial x^2}\right)_{{t}}$が正だということはその場所でグラフが下に凸だということである。二階微分の意味を考えると、「自分の両サイドの平均に比べて、自分の温度が低い」という状況を表している。このような時は温度は上がるだろう温度変化が線形（グラフが直線）のときは温度が時間変化しない。「温かい方から流れてくる熱と、冷たい方に奪われる熱が平衡している」状況だと考えよう。流れてくる熱量が温度差に比例すると近似して考えれば正しい。。

変数分離による一般解

　この式を変数分離で解く。すなわち、$\tau({t},{x})$をいきなり考えるのは難しいので、

のように、$\tau({t},{x})=T({t})X({x})$と${t}$の関数の部分と${x}$の関数の部分の積で表現されていると仮定し、これを代入してみる。$\left({\partial\left(T({t})X({x})\right)\over \partial t}\right)_{{x}} =K\left({\partial^2 \left(T({t})X({x})\right)\over \partial x^2}\right)_{{t}} $の左辺の${t}$による微分は$T({t})$にだけ掛かり、右辺の${x}$による微分は$X({x})$にだけ掛かるので、

\begin{equation} \begin{array}{rll} X({x}){\mathrm dT\over \mathrm dt}({t})=&K T({t}){\mathrm d ^2 X\over \mathrm dx^2}({x})\\[3mm] {{\mathrm dT\over \mathrm dt}({t})\over T({t})}=&K {{\mathrm d ^2 X\over \mathrm dx^2}({x})\over X({x})} \end{array}\label{heatbunri} \end{equation}

となるので、左辺と右辺が定数$\alpha$になると考えて、

\begin{equation} {{\mathrm dT\over \mathrm dt}({t})\over T({t})}=\alpha,~~K {{\mathrm d ^2 X\over \mathrm dx^2}({x})\over X({x})}=\alpha \end{equation}

の二つの常微分方程式を解けばよい。どちらも定数係数の斉次線形微分方程式だから、結果は

\begin{equation} T({t})= A \mathrm e^{\alpha{t}},~~X({x})=\begin{cases}B \mathrm e^{\sqrt{{\alpha\over K}}{x}} +C \mathrm e^{-\sqrt{{\alpha\over K}}{x}}&\alpha\neq0のとき\\ D{x}+E& \alpha=0のとき\end{cases} \end{equation}

であり$\alpha=0$の時に限り特性方程式が重解になるので別の解となる。、まとめると、

\begin{equation} \tau({t},{x})= \mathrm e^{\alpha{t}}\left( F \mathrm e^{\sqrt{{\alpha\over K}}{x}} +G \mathrm e^{-\sqrt{{\alpha\over K}}{x}} \right) \end{equation}

となる（$AB=F,AC=G$と置いた）。様々な$\alpha$の値全てに対して一個ずつ解があることになる。

テキストでは$\alpha=0$の場合を特別扱いして示してますが、授業では$\alpha\neq0$の場合のみを扱って、省略しました。

　線形微分方程式なので、実際の解はいろんな$\alpha$の解に対する和であり、

\begin{equation} \tau({t},{x})= \sum_{\alpha}\left( \mathrm e^{\alpha{t}}\left( F_\alpha \mathrm e^{\sqrt{{\alpha\over K}}{x}} +G_\alpha \mathrm e^{-\sqrt{{\alpha\over K}}{x}} \right)\right) \end{equation}

と書くことができる。係数$F,G$は各々の$\alpha$の値に対して別々に存在するので、$F_\alpha,G_\alpha$と添字をつけて区別することにした。

これで境界条件を指定しない場合の解を求めることができた。

境界条件と初期条件

　$H,J,F_\alpha,G_\alpha$を決めるためには初期条件と境界条件が必要である。ここでは境界は${x}=0$と${x}=L$だとしよう。境界条件は考えている現象に応じて選ばなくてはいけない。

　テキストでは三つの境界条件を示しているが、授業ではそのうち一つの例だけをやりました。

　簡単な例として、$\tau(t,0)=\tau(t,L)=0$という境界条件（つまり、両端で温度が0になる）場合について解いてみよう。

　まず$\tau({t},{x}=0)=0$という条件は$J=0$かつ全ての$\alpha$に対して$F_\alpha+G_\alpha=0$を意味する$\sum\mathrm e^{\alpha t}(F_\alpha+G_\alpha)=0$ではないのか？---と思う人がいるかもしれないが、任意の時間でこの和が0になるためには、係数$(F_\alpha+G_\alpha)$が全ての$\alpha$に対して0にならなくてはいけない。。そこで$J=0,G_\alpha=-F_\alpha$として、

\begin{equation} \tau({t},{x})=\sum_\alpha F_\alpha\mathrm e^{\alpha{t}}\left( \mathrm e^{\sqrt{{\alpha\over K}}{x}} -\mathrm e^{-\sqrt{{\alpha\over K}}{x}} \right) \end{equation}

という形になる。次に${x}=L$での条件を考えると、

\begin{equation} \tau({t},{x}=L)=\sum_\alpha F_\alpha\mathrm e^{\alpha{t}}\left( \mathrm e^{\sqrt{{\alpha\over K}}L} -\mathrm e^{-\sqrt{{\alpha\over K}}L} \right)=0 \end{equation}

となるが、任意の時刻で0になるためには、全ての$\alpha$に対して

\begin{equation} \mathrm e^{\sqrt{{\alpha\over K}}L} -\mathrm e^{-\sqrt{{\alpha\over K}}L}=0 \end{equation}

となる必要がある。上の式を変形すると$\mathrm e^{2\sqrt{{\alpha\over K}}L}=1$だが、「$\mathrm e^0=1$だから$2\sqrt{{\alpha\over K}}L=0$」と考えてしまうと$\alpha=0$になる。

　気をつけなくてはいけないのは$\mathrm e^{2\pi\mathrm i}=1$（あるいは、これを$n$乗して（$n$は整数）、$\mathrm e^{2n\pi\mathrm i}=1$）ということで、これから、

\begin{equation} 2\sqrt{{\alpha\over K}}L=2n\pi\mathrm i~~~すなわち、\alpha=-{n^2\pi^2 K\over L} \end{equation}

を解として採用できる$\alpha$は連続的な量ではなく離散的な量である。こうなることを知っていたので、$\sum_\alpha$のように和を書いた。。この条件から$\sqrt{{\alpha\over K}}= \mathrm i{n\pi\over L}$として代入すると、

\begin{equation} \tau({t},{x}) =\sum_{n>0}\tilde F_n \mathrm e^{-{n^2\pi^2K\over L}{t}}\left( \mathrm e^{\mathrm i{n\pi\over L}{x}} -\mathrm e^{-\mathrm i{n\pi\over L}{x}} \right) =\sum_{n>0}(2\mathrm i \tilde F_n) \mathrm e^{-{n^2\pi^2 K\over L}{t}}\sin {n\pi\over L}{x} \end{equation}

が境界条件を満たす一般解である。ここで、$\alpha$が$n^2\times(定数係数)$という形になったので、$F_\alpha$を$\tilde F_n$と書きなおした。解が実数であるためには、$\tilde F_n$は純虚数（$2\mathrm i \tilde F_n$が実数）である。以下は$2\mathrm i \tilde F_n=\tau_n$と書こう。また、上の式を見ると$n\to -n$と置き換えても結果は本質的に同じであることがわかるので、$n$の和は正の部分だけを取れば十分であるので、$\sum_{n>0}$とした。

　微分方程式の解としては、初期条件今考えている微分方程式は時間に関しては一階だから、初期条件は${x}$の一つの値に対して一つでよい。も満たさなくてはいけない。$\tau({t}=0,{x})=\tau_初({x})$を初期条件とする（$\tau_初({x})$は与えられた関数である）と、

\begin{equation} \tau_初({x})=\sum_{n>0}\tau_n\sin{n\pi\over L}{x} \end{equation}

になるように係数$\tau_n$を決めればよい。

　ここで、

\begin{equation} \tau({t},{x})=\sum_{n>0}\tau_n \mathrm e^{-{n^2\pi^2 K\over L}{t}}\sin{n\pi\over L}{x} \end{equation}

という式の物理的意味について考えておこう。この式には$\mathrm e^{-{n^2\pi^2K\over L}{t}}$がついている（しかも$n>0$）から、時間が立てば立つほど、温度は0に近づいていくことになる。今考えている状況は両端が温度0で、他に熱源はないのだから、十分に時間経過すれば全体の温度が0になるというのは「もっとも」なことである。$n$の違いはグラフで書いた時の「波の数」なので、より短い波長の温度分布（つまり頻繁に寒暖が入れ替わっている）ときに「早く冷める」というのは感覚的にも納得できるだろう。

最初からやり直し停止／再開

---

平坦に戻す 直線にする（両端は変えない） n=1の状態にする n=2の状態にする n=3の状態にする

偏微分方程式の解き方 波動方程式

波動方程式

\begin{equation} \left({\partial^2 u({t},{x})\over \partial t^2}\right)_{{x}} =v^2\left({\partial^2 u({t},{x})\over \partial x^2}\right)_{{t}} \end{equation}

という微分方程式を解いてみよう。

　実はこれは音などの「波」の方程式である。左辺は時間の二階微分だから加速度で、それは波の媒質（考えている波が音ならば空気、海の波なら海水）に働く力に比例する。右辺も力に比例するのだが、それが${x}$に関する二階微分になっている。二階微分は「曲がり具合」を意味するのであった。ここで海にできる波をイメージして、$u({t},{x})$はある時刻におけるある場所の海面の高さだとしよう。右辺の${x}$による二階微分は「海面の曲がり具合」を意味する。それが正なら海面は「谷」になり、負なら「山」になっていると思えばよい。海の波においては「山」なら下向きの、「谷」なら上向きの力が働くだろう、と考えると上の式の意味がわかるもちろん、海水に働く力をちゃんと計算して式にしていくと（適切な近似を行う必要はあるが）上の式が出てくる。ここではこの式の意味を解釈するだけでよしとしよう。。熱伝導方程式では${x}$の二階微分がそのまま温度の時間変化になったが、波の方程式の場合は${x}$による二階微分は「時間変化の時間変化」（すなわち加速度）になる。

↓波のグラフ

↓速度のグラフ

最初からやり直し停止／再開

初期状態を平坦に戻す n=1の波にする n=2の波にする n=3の波にする

初速度を 0にする n=1の波にする n=2の波にする n=3の波にする

---

熱伝導方程式 受講者の感想・コメント

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

偏微分の応用