自然科学のための数学2015年度第6講
グラフの傾きを知る方法
関数の局所的ふるまいを知る
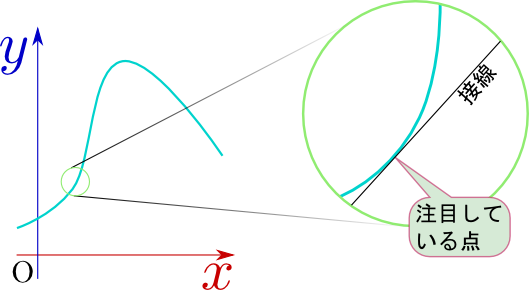
関数を考える時、「ある点の近所での様子」だけを知ればよい、ということがある。この「近所の様子」を「局所的なふるまい」と呼ぼう。逆に全体を見てわかるのが「大局的ふるまい」である。局所的なふるまいを知るには、「その点での値」と「その点での傾き(正確には背線の傾き)」を知れば十分な場合がある。この章で考える微分という計算は「傾き」を知るという目標のためにある。
次に重要な情報は「今値上がり中か?」(変化=傾き)である。
今値上がり中なら「今のうちに入れておかないと明日はもっと高くなる」と、値下がり中なら「入れるのは明日にしよう」などと決断できる。
詳細な「予言」のためにはもっとデータが必要だが、「今日ガソリンを入れるか」の決断なら、「値」と「傾き」がわかっていれば十分である。
なお、さらに次の情報としては「曲がり具合」なのだが、それはまた次の段階で考えよう。
傾きしかわからないのでは知るべき情報が足りないのではないか?
と思うかもしれない一方で「局所的なふるまい」という情報を取り出すことで、全体を俯瞰していたのではわからないことに気づくことだってある。。それはもちろんのことであるが、実は我々は「大局的なふるまいから局所的なふるまいを知る方法」、逆に「局所的なふるまいから大局的ふるまいを知る方法」、その両方を持っている。ここではまず前者の方を考えよう、というわけである。
この方法は万能というわけではないが、ありがたいことに自然法則というのは局所的な法則になっていることが多い。少なくともこれまでの科学の歴史においてはまず局所的ふるまいを知り、それから大局的法則を出す、という筋道で理論を組み立てて結果として成功したこと(ニュートン力学がまさにこれ)が多い。だからこそ、局所的なふるまいを計算する方法である微分が自然科学において重要な役割をになうことになる。
例として、関数$y=x^2-x$を考えよう。この関数の原点での値は0であり、グラフを書いてみると傾きは1である。この傾きが1であるということを知る方法として、$x^2$の項は$x=0$付近では効かないとして忘れる、という方法がある(これまでの授業で「次数の高い項は関係ない」という話を繰り返ししたのは、この感覚に馴染んでもらうため)。
では、$x=1$付近を考えるときにはどうしよう。
もちろん、「微分する」ってのが答なんだけど、ここはその微分ってどんな計算か、ということを説明しようと思っているところなので、とりあえず「微分は知らないふり」で答えてくださいということで聞き直すと、
直前と直後の値を計算して変化を見る。
という答えが出てきた。
この計算はもちろん、微分の考え方そのものである。
ところで、もう1つの計算方法がある。我々は$x=0$付近での傾きの計算方法は知っているから、関数を平行移動して$x=1$が原点に来るように変えてしまう($y=x^2-x \to y=(x+1)^2-(x+1)$)という手もある。
こうして計算すると$y=x^2 + x$となるから、この点での傾きは1である。
極限としての接線の傾き
上で出てきた「直前と直後の値を計算」に近い計算で傾きを出してみる。
${y}=f(x)=x^2$という、単純な関数の場合で傾きの計算をしてみよう。直前というのは$x=1$にして、直後は「$x$が1よりちょっと大きいところ」にしよう。
x=1として、Δxを変化させていった時の各項の様子を表にしてみると、
| Δx | x+Δx | (x+Δx)2 | 2xΔx | (Δx)2 | 2x+Δx |
|---|---|---|---|---|---|
| 1 | 2 | 4 | 2 | 1 | 3 |
| 0.1 | 1.1 | 1.21 | 0.2 | 0.01 | 2.1 |
| 0.01 | 1.01 | 1.0201 | 0.02 | 0.0001 | 2.01 |
| 0.001 | 1.001 | 1.002001 | 0.002 | 0.000001 | 2.001 |
| 0.0001 | 1.0001 | 1.00020001 | 0.0002 | 0.00000001 | 2.0001 |
のようになる。Δxを小さくするに従って、${{\Delta y}\over {\Delta x}}$は2に近づく。つまり、「Δxが0に近づいた時の値」が2である。
いちいちこうやって数字で計算するのもたいへんなので、一般的な式を出そう。
独立変数と従属変数であるxと${y}$は${y}=x^2$という関係式を満たしながら変化するのだから、変化後も
\begin{equation} \underbrace{{y+\Delta y}}_{変化後の{y}}=(\underbrace{{x+\Delta x}}_{変化後のx})^2 \end{equation}という式が成立する。この式の右辺を$({{x+\Delta x}})^2=x^2 + 2{x\Delta x} + ({\Delta x})^2$と展開した後、元の式${y}=x^2$と辺々の引き算を行なう。
 \begin{equation}
\begin{array}{rrrll}
& {y}&+{\Delta y}=&x^2+&2{x\Delta x}+({\Delta x})^2 \\
-)& {y}&=&x^2 &\\ \hline
&&{\Delta y} =&& 2{x\Delta x}+ ({\Delta x})^2
\end{array}\label{dy2xdx}
\end{equation}
\begin{equation}
\begin{array}{rrrll}
& {y}&+{\Delta y}=&x^2+&2{x\Delta x}+({\Delta x})^2 \\
-)& {y}&=&x^2 &\\ \hline
&&{\Delta y} =&& 2{x\Delta x}+ ({\Delta x})^2
\end{array}\label{dy2xdx}
\end{equation}
こうして二つの変数の変化量の間は、${\Delta y}=2{x\Delta x}+({\Delta x})^2$という関係があることがわかった。当たり前だが、${\Delta x}=0$と置くと、${\Delta y}=0$になる。
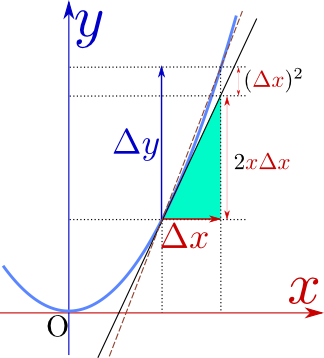
ここで、
\begin{equation} {{\Delta y}\over {\Delta x}}=2x+{\Delta x} \end{equation}となるが、この量は図に破線で描いた直線の傾きになる。
試しに${\Delta x}=0.01$としてみると、$\left({\Delta x}\right)^2=0.0001$になる。つまりΔxをどんどん小さくするという文脈において、$\left({\Delta x}\right)^2$は「Δxより、もっと小さい」量になっている。
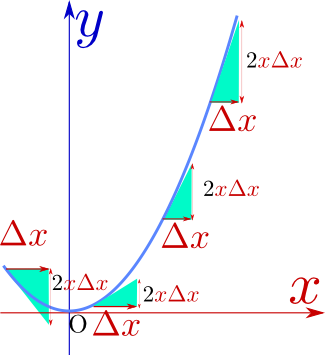
${\Delta x}\to0$という極限を取っていくと(この時同時に${\Delta y}$も0に近づくわけだが)、第2項はなくなってしまって、
\begin{equation} \lim_{{\Delta x}\to0}{{\Delta y}\over {\Delta x}}=2x\label{diffxsq} \end{equation}がわかる。つまり接線の傾きは$2x$である。xが変化すると傾き${{\Delta y}\over {\Delta x}}$が変化する様子を示したのがt次のグラフである。
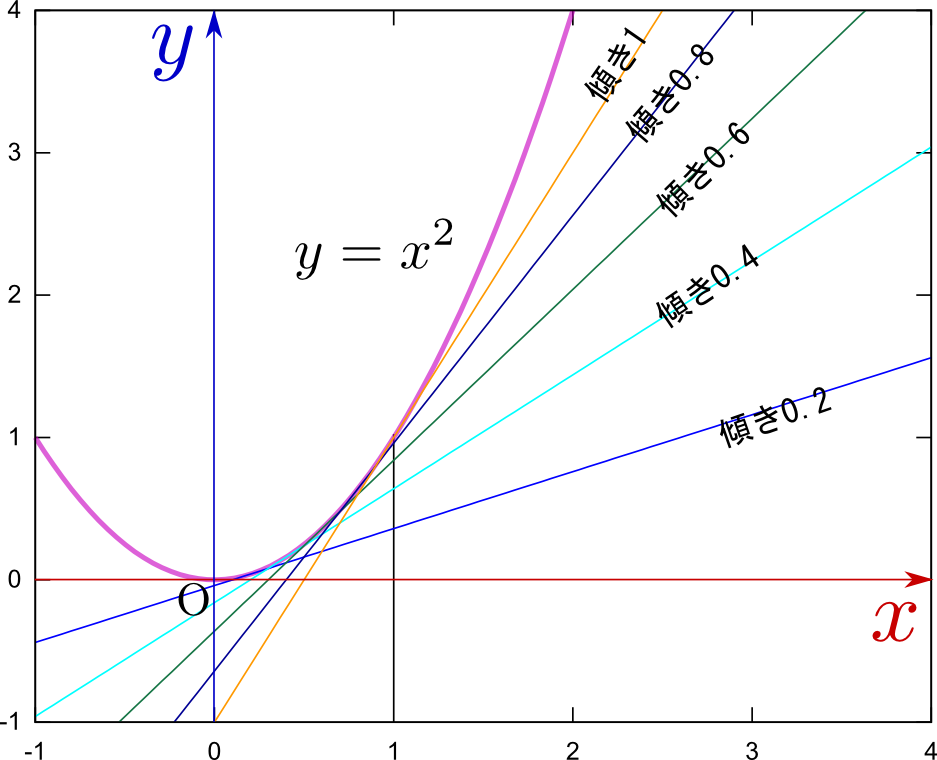
各々の場所において接線の傾きが変化しつづけている。$x<0$では傾きも負になっていることに注意しようx=0のところでは傾き0、すなわち水平な線が接線となる。しかし、図では高さ0の三角形になって見えなくなってしまうので描いていない。}。