$\mathrm d$という記号

　${\Delta x}$や${\Delta y}$は「変化量」という意味があった。微分を行う時は、${\Delta x}$を0に近づける（連動して、${\Delta y}$も0に近づく）。このようにここから先の計算ではしばしば、${\Delta x}$や${\Delta y}$に「変化量」という意味に加えて「0に近づく」という属性が加わる。この「0に近づけていく変化量」という量を表すために、新しい記号として$\mathrm dx,\mathrm dy$を導入しよう。つまり、$\Delta$の替りに$\mathrm d$という記号を使って後で$\to0$という極限を取ることが約束されている変化量を示すことにする。本講義で$\mathrm dx$とか$\mathrm dy$ のように$\mathrm d$のついた量は、すべて「微小変化」を表現する量である。

$\mathrm dx$や$\mathrm dy$を「微小変化」と呼ぶが、この呼び方は少し説明が不足していて、単に「微小」ではなく「0になる極限を取る」という点が重要である。

あるいは「微小」という考え方がしっくりこない、という人は以下のように考えてもよい。

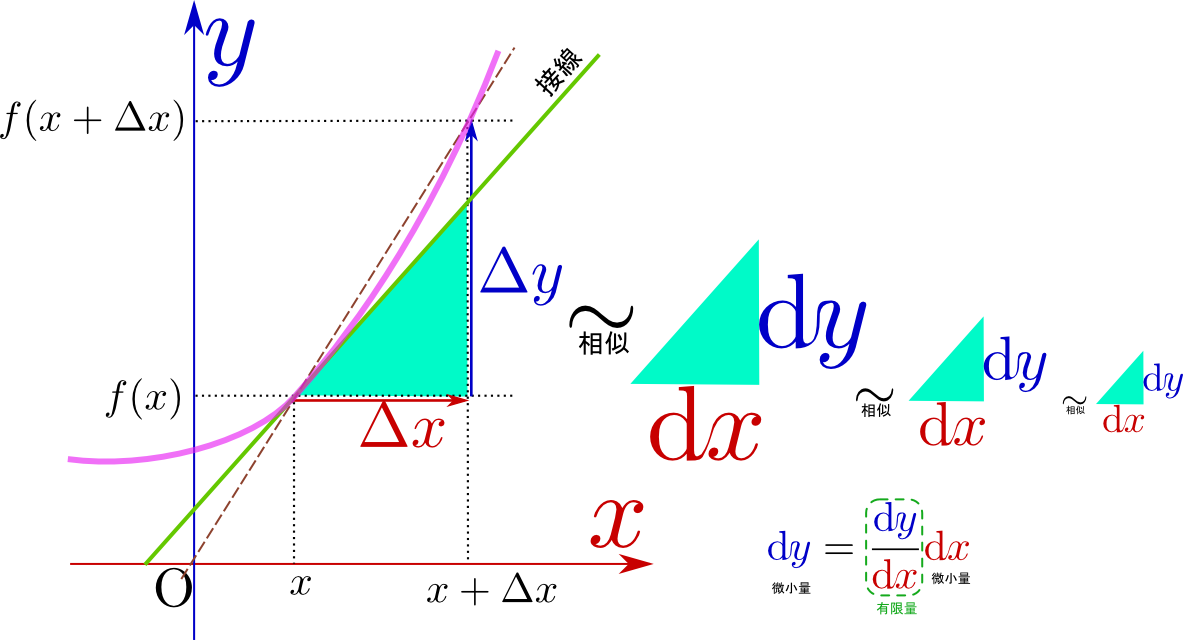
上の図にも示したように、$\mathrm dx$や$\mathrm dy$はあくまで、のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える（この考え方なら微小である必要はない）。そして、$\mathrm dx$ や$\mathrm dy$そのものの大きさは重要ではなく、という形（どんな直角三角形か？）、あるいは「$\mathrm dx$ と$\mathrm dy$の比」が重要であって、$\mathrm dx$ や$\mathrm dy$そのものは大きさを考えてはいけない（考えても意味はない）量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy$の二つで向きを表現する量」なのである。

　${\mathrm dy\over \mathrm dx}$は普通の数（大きさを考える意味がある）だし、$\mathrm dy=a\mathrm dx$と書いた時の$a$も普通の数である。だから${\mathrm dy\over \mathrm dx}=2$や$\mathrm dy = 0.7\mathrm dx$は意味のある式である。しかし、$\mathrm dx=1$とか$\mathrm dy=0.02$などという式には全く意味がない=0だけは、「$\mathrm dx=0$の極限をとって」のように使うこともあるが、本来はあまりよい使い方ではない。。$\mathrm dy$ や$\mathrm dx$は、二つがペアになって接線の向きを表現している量であって、$\mathrm dx$ のみの大小を云々してはいけない。

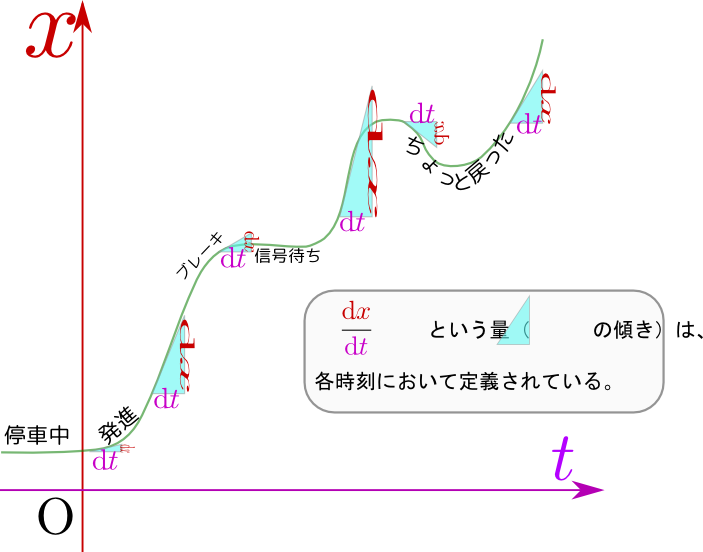
　新しい記号を使えば、接線の傾きは${\mathrm dy\over \mathrm dx}$になる$\mathrm dx$や$\mathrm dy$は、接線という直線の上での長さを表現しているという考え方もできる。。この${\mathrm dy\over\mathrm dx}$、厳密に書けば

$$\begin{equation} {\mathrm dy\over\mathrm dx}=\lim_{{\Delta x}\to0}{{\Delta y}\over {\Delta x}} \end{equation}$$

が導関数（もしくは微係数）である。$\mathrm dy$ と$\mathrm dx$は微小量、すなわち0になる極限を取るべき量だが${\mathrm dy\over \mathrm dx}$は有限な量である。

　こうして「傾き」という量を$x$の関数として表現する方法を我々は得た。最初に書いた${{\Delta y}\over {\Delta x}}$という量は、ある「幅」${\Delta x}$があって（その「幅」の間での変化の割合として）初めて定義できる量だったが、${\mathrm dy\over \mathrm dx}$の方は、「一点」$x$で決まる量であることに注意しよう。

　これで${\mathrm dy\over \mathrm dx}$という量が「接線の傾き」という数字として意味のある量となったので、${\mathrm dy\over \mathrm dx}$で一つの量、として扱うことにする。この量もまた$x$の関数であることを表現するため、${\mathrm dy\over \mathrm dx}(x)$のように$(x)$という引数を付けて書く。この書き方はf(x)の$f$のところに${\mathrm dy\over \mathrm dx}$が入った形で、${\mathrm dy\over \mathrm dx}$が「関数名」として機能している（だから、${\mathrm dy\over \mathrm dx}$で1文字であるかのごとく扱う）${\mathrm dy\over \mathrm dx}$は「でぃーわいでぃーえっくす」と分子・分母の順にいっきに（「これで一文字だよ」って感じで）読む。分数のようなものではあるが、「でぃーえっくす、ぶんの、でぃーわい」とは読まない。。

　これが導関数（もしくは微係数）を${\mathrm dy\over \mathrm dx}(x)$のように書く理由である。f'(x)の方はニュートンによる記号で、$f$という関数から$f'$を作ったということをよく表現できている記号である。一方${\mathrm dy\over \mathrm dx}$はライプニッツの記号で、何の変化と何の変化の比を考えているのかがよく表現できている記号である。これらの記号は使いどころによって一長一短がある。

　$\mathrm dy=f'(x)\mathrm dx$とした時、$f'(x)={\mathrm dy\over \mathrm dx}(x)$であるが、これを${\mathrm df\over \mathrm dx}(x)$と書くこともある（関数を意味する$f$を変数の意味にも使っている）。$\mathrm dy={\mathrm df\over \mathrm dx}(x)\mathrm dx$と書いた場合、導関数を求めるという計算$f(x)\to f'(x)$は、$f(x)\to {\mathrm df\over \mathrm dx}(x)$となる。この計算は、あたかも、「f(x)に${\mathrm d \over \mathrm dx}$が掛かった」ように見える。そこで、同じ式を$f(x)\to {\mathrm d \over \mathrm dx}f(x)$と書くこともある。

　この${\mathrm d \over \mathrm dx}$のような記号$y$で微分する${\mathrm d \over \mathrm dy}$などもあるし、ずっと後では偏微分${\partial\over \partial x}$などのような微分演算子も出てくる。を「微分演算子(differential operator)」と呼ぶさらには${\mathrm d \over \mathrm dx}$と書くのも面倒臭がって$D$一文字で表すこともある。。