微分の性質・公式など
微分の意味
もう一度微分の定義を、以後で使いやすい形でまとめると、
$\underbrace{f(x+\mathrm dx)}_{変化後の量}=\underbrace{f(x)}_{元の量}+ \underbrace{f'(x)\mathrm dx}_{変化量}$
のように書くことができる。この$\mathrm dx$の前の係数$f'(x)$が「$f(x)$の導関数(微係数、または微分)」と呼ばれる量である。となる。
ライプニッツ則
前回微分の性質として線形性を述べたが、今日はまず「ライプニッツ則」を述べよう。ライプニッツ則とは
${\mathrm{d} \over \mathrm dx}\left(f({x})g({x})\right)=\left({\mathrm{d} \over \mathrm dx}f({x})\right)g({x})+f({x}){\mathrm{d} \over \mathrm dx}g({x})$
または
$(f({x})g({x}))'=f'({x})g({x})+f({x})g({x})$
という式。つまり、
ということ。具体的には、
\begin{equation} \begin{array}{rl} f({x}+\mathrm dx)g({x}+\mathrm dx) =&\underbrace{(f({x})+f'({x})\mathrm dx)}_{\small f({x}+\mathrm dx)}\underbrace{(g({x})+g'({x})\mathrm dx)}_{\small g({x}+\mathrm dx)}\\ =&f({x})g({x})+f'({x})g({x})\mathrm dx+f({x})g'({x})\mathrm dx\\[3mm] =&f({x})g({x})+\underbrace{(f'({x})g({x})+f({x})g'({x}))}_{(f({x})g({x}))'}\mathrm dx\\ \end{array} \end{equation}という計算をやると、右辺の$\mathrm dx$の1次のオーダーの係数(つまり、微係数)が$f'({x})g({x})+f({x})g'({x})$であることがわかる。下の図はこの微分演算の時に行われている微小変化のイメージである。
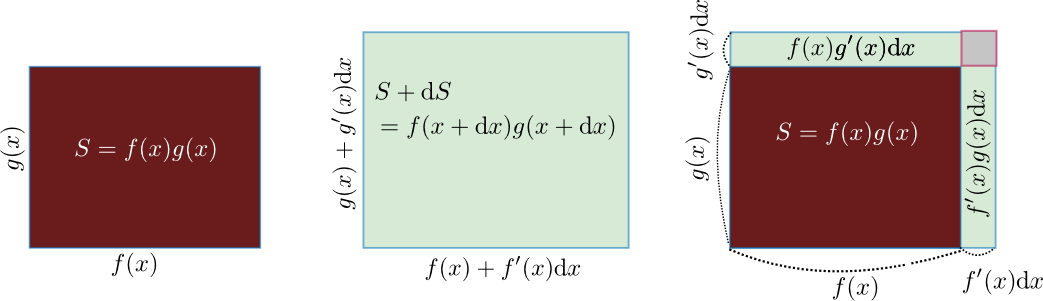
合成関数の微分
合成関数の微分(このルールは「連鎖律(chain rule)」とも呼ばれる)を数式で表現しておこう。$g(f({x}))$という合成関数を考えて、その独立変数${x}$を${x}+\mathrm dx$と微小変化させる。
結果、$f({x})$は
\begin{equation} f({x}+\mathrm dx)= f({x})+ \underbrace{f'({x})\mathrm dx}_{\mathrm{d} (f({x}))} \end{equation}へと変化する。ここで$\mathrm{d} (f({x}))=f'({x})\mathrm dx$という記号を使った。$\mathrm{d}(なんとか)$のように$\mathrm{d} $をつけることで「(なんとか)の微小変化」という意味を持たせるこれをさらに省略して$\mathrm df({x})$、さらに$({x})$も省略して$\mathrm df$とだけ書いたりもする。。ライプニッツの記号の方を使うと、$\mathrm{d} (f({x}))={\mathrm df\over \mathrm dx}({x})\mathrm dx$と書けて、この式を「$\mathrm dx$を約分している」というイメージで捉えることができる。
$f({x})$の${x}$が微小変化すると、$g(f({x}))$は
\begin{equation} g(f({x}+\mathrm dx))= g(f({x})+\underbrace{f'({x})\mathrm dx}_{\mathrm{d}(f({x}))}) \end{equation}と微小変化する。上にも書いたように、$f'({x})\mathrm dx$の部分を$\mathrm{d} (f({x}))$と考えれば、
\begin{equation} g(f+\mathrm{d} (f({x})))= g(f)+g'(f)\mathrm{d} (f({x})) \end{equation}という展開をもう一度考えて、
\begin{equation} g(f({x}+\mathrm dx))= g(f({x}))+ g'(f({x}))\underbrace{f'({x})\mathrm dx }_{\mathrm{d} (f({x}))} \end{equation}とすることで、$g(f({x}))$の導関数が$g'(f({x}))f'({x})$だとわかる。
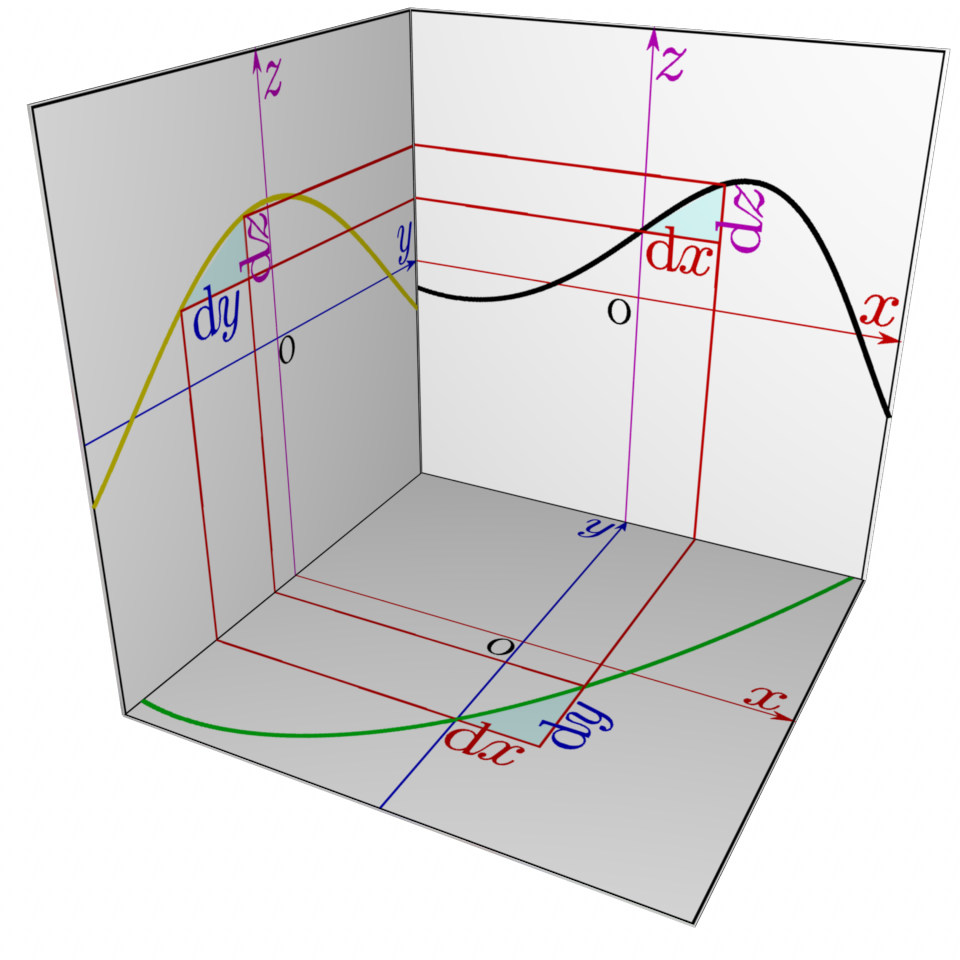
これを図で表現したのが右の図である。合成関数のときのように、${x}\to{y}\to{z}$(${y}=f({x}),{z}=g({y})$)という関係がある時、${x}$を微小変化させた時にそれに応じて${y}$が、そして連鎖して${z}$が変化する。
図には三つの導関数
$${\mathrm dy\over \mathrm dx}({x}),{\mathrm dz\over \mathrm dy}({y}),{\mathrm dz\over \mathrm dx}({x})$$を表す三角形(この三角形の傾きが導関数の値)が描かれている。導関数は$\mathrm dx,\mathrm dy,\mathrm dz$という三つの微小量の比でここでも計算しているのは微小変化の「比」だけであって、微小変化そのものではない。計算されるものだから、
\begin{equation} {\mathrm dz\over \mathrm dy}({y}) {\mathrm dy\over \mathrm dx}({x})={\mathrm dz\over \mathrm dx}({x})~~~~ただし、{y}=f({x}) \end{equation}が成立する。
\begin{equation} {\mathrm dz\over {\mathrm dy}}{{\mathrm dy}\over \mathrm dx}={\mathrm dz\over \mathrm dx} \end{equation}という「約分」を行った、と考えてもよい。
例として$F({x})=({x}^2+{x})^3$の微分をしてみよう。これを$f({y})={y}^3,{y}=g({x})={x}^2+{x}$として、$F({x})=f(g({x}))$と考えてから微分すると、
\begin{equation} {\mathrm{d} \over \mathrm dx}F({x})=\underbrace{ {\mathrm{d} \over \mathrm dx}g({x})}_{(2{x}+1)} \underbrace{ {\mathrm{d} \over \mathrm dy}f({y})}_{3{y}^2} = 3(2{x}+1)({x}^2+{x})^2 \end{equation}となる。慣れてきたら${y}$を導入するのも省略して、
\begin{equation} \begin{array}{rrl} & ({x}^2+{x})^3+ \mathrm{d} \left(({x}^2+{x})^3\right)=& \left( {x}^2 + {x} + \mathrm{d} ({x}^2+{x}) \right)^3 \\ &\mathrm{d} \left(({x}^2+{x})^3\right)=& \left( {x}^2 + {x} + \mathrm{d} ({x}^2+{x}) \right)^3- ({x}^2+{x})^3\\ &\mathrm{d} \left(({x}^2+{x})^3\right)=&3\left( \mathrm{d} ({x}^2+{x})\right) ({x}^2+{x})^2\\ &=&3(2{x}+1)({x}^2+{x})^2\mathrm dx \end{array} \end{equation}のように計算したってよい。
分数関数の微分
${y}={1\over f({x})}$の微分の公式を出そう。
ライプニッツ則を使うなら、まず${y}f({x})=1$と直してから
\begin{equation} \begin{array}{rll} {y}f({x})=&1&{↓微分}\\ \underbrace{\mathrm dy}_{前を微分} f({x})+{y}\underbrace{f'({x})\mathrm dx}_{後を微分} =&0&{↓移項}\\[2mm] \mathrm dy f({x})=& -\overbrace{{1\over f({x})}}^{{y}}f'({x})\mathrm dx\\[4mm] {\mathrm dy\over \mathrm dx}=& -{f'({x})\over \left(f({x})\right)^2} \end{array}\label{bunsuubibunone} \end{equation}として計算することができる。
合成関数の微分を使うなら、まず$g(y)={1\over y},y=f(x)$と二段階の合成関数にしてから
\begin{equation} {\mathrm d\over \mathrm dx}g(y)=g'(y)\times f'(x)=-{1\over (f(x))^2}\times f'(x) \end{equation}とすればよい。
逆関数の微分
関数${y}=f({x})$の逆関数${x}=f^{-1}({y})$を微分するとどうなるか。導関数は${従属変数の微小変化\mathrm dy \over {独立変数の微小変化\mathrm dx} } $という比で計算される。${\mathrm dy\over \mathrm dx}=f'({x})$なのだから、${\mathrm dx\over \mathrm dy}={1\over f'({x})}$なのは当たり前である。よって、
\begin{equation} {\mathrm dx\over \mathrm dy}({y})={1\over f'({x})}\biggl|_{x=f^{-1}({y})}~~~~(f'({x})を計算したのち、xにf^{-1}({y})を代入)\label{gyakubibun} \end{equation}という結果になる。つまりは「逆関数の微分は関数の微分の逆数」である。

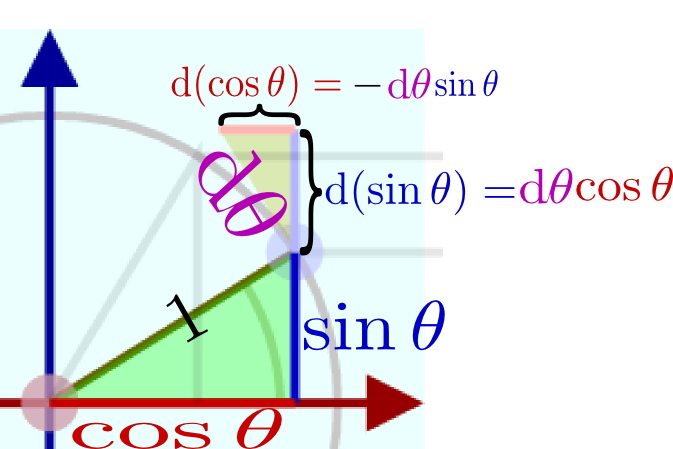
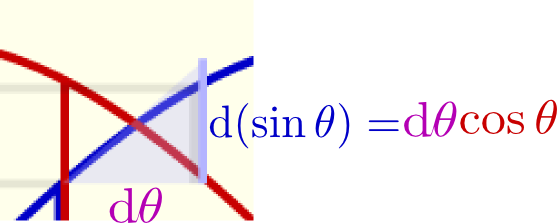 のように傾きが表示してある。この「傾き」が確かに
のように傾きが表示してある。この「傾き」が確かに