青字は受講者からの声、赤字は前野よりの返答です。
微分のいろいろな公式の意味を知ることで、ただ暗記するより何倍も理解が深まったように思います。
「使うための数学」は暗記ではダメですよ。
三角関数、指数関数、対数関数の微分を、今までは公式として覚えていたが、その公式に至るまでの過程をじっくりと考えていった。図と計算、二つの方法から導き出すことで、より深い理解ができてよかったです。
「来週の試験のために」というその場しのぎならしょうがないですが、本当に「身につく」ためには「公式として覚える」勉強をしてはいけません。
sinθ、cosθ、tanθの微分がわかった。
それはよかった。
様々な関数の関数の微分について詳しく学んだ。高校の時とは違う視点で学んだのでとても興味深く、より理解が深まった。
微分のイメージを持つようにしていってください。
面白い内容でした。わかりやすかったです。
面白さを感じつつ、勉強していってください。
$\mathrm e^x\fallingdotseq1+x$はテイラー展開ですね!!
はい、テイラー展開はすぐ後でやりますが。
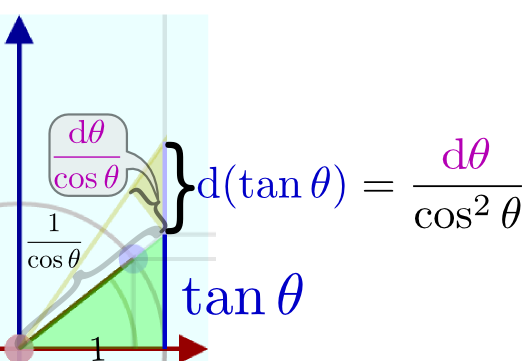
tanの微分が難しかった。
自分で一度やってみてください。
三角関数の微分や対数関数の微分の仕方を学ぶことができてよかった。
それはよかった。
$\log x\to{1\over x}$の異様さはそのままなんかい!! 1本取られたわ。
異様?? 異様かなぁ?
同じ「微分する」という言い方でもいろんな種類のものがあるということを学んだ。
要は「微小変化の割合を考える」ってことなんですけどね。
対数関数は救世主だったのか…。
救世主は大げさだけど、logのおかげで助かることはよくあります。
今日はねむすぎた。
そうですか。
昨日微分方程式の勉強をしていて「思いつけないんだけどー!」と思っていたのですが、今日の授業で$\mathrm e^x$の微分は元の関数と同じ」というのを聞いて全部意味があってつながっているのをとても感じました。
exp(x)のおかげで解ける微分方程式は、とてもたくさんあります。
微分の先輩がよくする間違い、自分もしそうなので例に出してもらってよかったです。気をつけたいと思います。
やっちゃわないように気をつけましょう。
最後に出てきた$f'({x})=f({x})\times {\mathrm d \over \mathrm dx }\log \left(f({x})\right)$には感動しました。自宅でも微分の演習を頑張りたいと思います。
いろんな演習をやってみてください。
logの微分難しかったです。cos(α+β)の公式がなんで−になるのか知れてよかったです。
今日やったのは微分の式で、加法定理とは別ですが、確かにマイナスになる理由は同じですね。
先生が一番かっこいいと思う四文字熟語はなんですか? 僕は「波動関数」ですね。
う〜〜ん。「繰込可能」かな。
「微分する」に二つの意味があるとは知らなかった。問題で出たとき、どちらの意味であるか考えたりするのかなと思った。
文脈でわかります。
$f(x+\mathrm dx)=f(x)+f'(x)\mathrm dx$の重要さがだんだんわかってきた。
微分の意味がわかってくると、あの書き方の便利さがわかってきます。
微分の2種類の意味がわかった。
2種類といいつつ、どっちもまぁ「微小変化考える」というのは同じです。
指数・対数関数の微分の中身がわかりやすくて理解できた。
それはよかった。
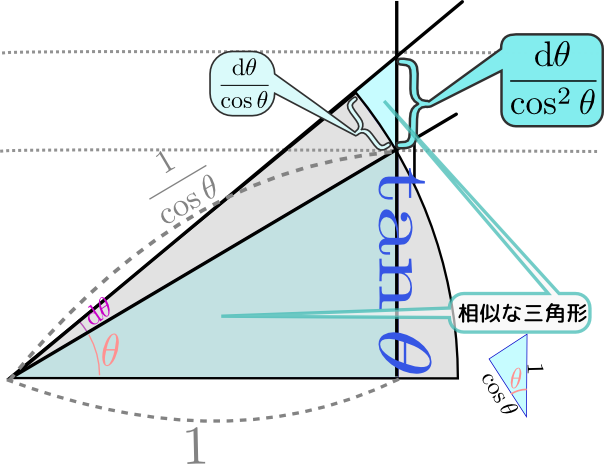
図を使って考える三角関数の微分は少し難しいけど面白かったです。
図でいろいろ考えてみてください。
${\mathrm d\over \mathrm dx}x^x$の仕方がわからなかったが、今日で$f'({x})=f({x})\times {\mathrm d \over \mathrm dx }\log \left(f({x})\right)$が理解できたので、すごく計算が楽に感じた。あと、微小変化の意味もなんとなくわかった。
いろんな計算方法を、うまく使って計算していってください。
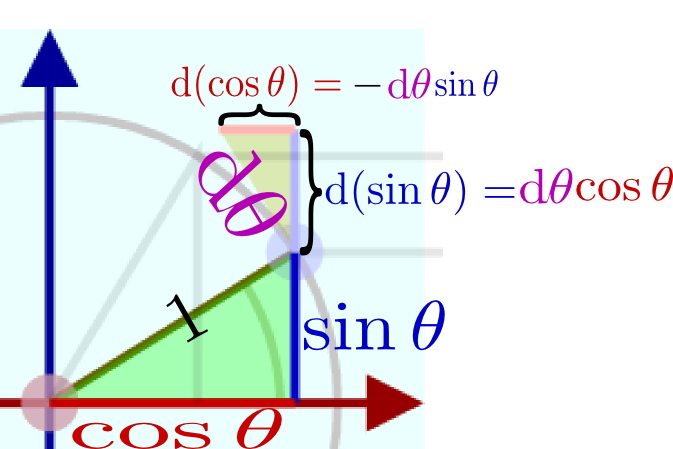
$\cos\theta$の微分に−がつくのは微小増加を取ったときに$\sin^2\theta+\cos^2\theta=1$と一定になる必要があるからという説明にとても納得がいった。
いろんな式を、成り立ちから理解しておきましょう。
$f'({x})=f({x})\times {\mathrm d \over \mathrm dx }\log \left(f({x})\right)$がとても便利で感動しました。三角関数の微分を説明した図形がとてもわかりやすかったです。
微分はいろんなやり方があるので、使い方を理解しておきましょう。
合成関数の微分と、ネイピアの数。
う〜ん、どっちも今日じゃなく前にやったことを使っただけなんだけど。
逆関数・指数関数の微分を学んだ。数IIIでやった「微分可能」の定義や「連続する」の定義をもう一度復習したい。
そのあたりの話はこの授業では少ししか取り上げないので、是非復習しておいてください。
$x^x$のようなものからライプニッツ則まで、logを使って簡単に説明できるとわかって驚きました。
logやexpっていろんなところで役に立つんですよ。
図と計算で三角関数の微分が理解できました。
両方で理解するのが大事です。
微小で増加量を求めたら、微分と同じ。
微分というのは、そういうものです。
微分よくわかった。逆関数の微分がよくわかった。
それはよかった。
$\sin(\theta+\mathrm d\theta)=\sin\theta\underbrace{\cos\mathrm d\theta}_1+\cos\theta\underbrace{\sin\mathrm d\theta}_{\mathrm d\theta}$で$\cos\mathrm d\theta=1,\sin\mathrm d\theta=\mathrm d\theta$になる理由がわからない。
$\sin\mathrm d\theta$が$\mathrm d\theta$なら、$\sin(\theta+\mathrm d\theta)=\sin\theta+1$?
わからないことはその時すぐ質問しないと。$\sin\mathrm d\theta\simeq \mathrm d\theta$は先週説明した話なので復習してください。そのとき、$\cos\mathrm d\theta\simeq 1-{(\mathrm d\theta)^2\over 2}$となることも説明したはず。あと最後の式は、ちゃんと計算すると$\sin(\theta+\mathrm d\thata)=\sin\theta+\cos\theta\mathrm d\theta$になります。
もう一週早くこの内容をやってくれれば、昨日の微積のテストがもう少しましな点数がとれたのに残念です。
それは残念でした。
微積STの中間テストで出たところを今日先生がやってくれて、全然できてないなー(テストが)と思いました。
それは残念なお知らせです。
図を作って微分を考えることができた。
いろんな考え方をやっていきましょう。
変数の変数乗をかんがえるときlogに直して計算すると微分もできることがわかった。$lim_{x\to0}{\log(1+x)\over x}=1$ですか?
その極限は確かにそうなります。
もし${\mathrm d\over \mathrm d\theta}\cos\theta$や${\mathrm d\over \mathrm d\theta}\tan\theta$を忘れてしまっても(そんなことはないけど)、${\mathrm d\over \mathrm d\theta}\sin\theta$さえわかっていれば順次求められるので、いざというときに便利(多分)。arc型の微分もそこまで難しくなかった。気になることだが陰関数やリサージュ曲線も微分や微分係数を求めることができるのだろうか。理論上可能だと思うが、答えが複数になりそう…。
複数の値がある場合は、微分も場合分けなどの注意が必要ですね。
色々なことが頭の中でごちゃごちゃしてきた。一回今までの復習をして、全体を見直したい。
うん、整理は大事。
三角関数の微分でいろんな説明の仕方があっておもしろかった。
1つのことをいろんな方向から見てみましょう。
sinθとcosθの微分の成り立ちがよくわかった。$\mathrm e^x\fallingdotseq 1+x,x\fallingdotseq \log(1+x)$
いろんな式を結びつけて理解しておいてください。
微分の参考書とかで、$\mathrm e$(ネイピア数)を使った証明が出てくるのですが、よくわかりません。ネイピア数の式とか性質みたいなものを簡単に解説してくれる本を教えてくれませんか。$\lim_{n\to\infty}\left(1+{1\over n}\right)^n=\mathrm e\to \lim_{n\to\infty}\left(1-{1\over n}\right)^n={1\over \mathrm e}$
今配っている教科書にも(そして、その他のたいていの教科書にも)必要なことは書いてあると思いますが、それではどこが「よくわからない」のでしょう?
その式は成立しますね。極限を取る計算をやってみましょう。
物理学Iを習っていたときに疑問が残っていたsinθやcosθを微分した時に残るdθというのは、変化量を見た場合の計算をしていることがわかりました。高校までの知識は大学で逆に混乱するかもしれないので、大学の勉強をしっかりしていきたいと思います。$\mathrm e$の知識がより深めることができたのでよかったです。
大学の教科書は高校までと違って文科省検定なんてものはないので、書き方は統一されてないですが、そこは臨機応変に読むようにしてください。
関数が好きになれるよう頑張りたい。
好きになりましょう、長いつきあいです。
三角関数を絵で理解すると分かりやすかった。
図と式の両方で理解しておきましょう。
$f'({x})=f({x})\times {\mathrm d \over \mathrm dx }\log \left(f({x})\right)$という式は今まであまりみたこyとがなかったので覚えておきたい。
基本は合成関数の微分です。
$\mathrm e^x$の微分が$\mathrm e^x$のままなのがわかった。
この性質が後々いろいろと役に立ちます。
微小変化を求める微分のやり方に慣れるために頑張りたいと思った。
慣れていきましょう、慣れると便利。
三角形の図と対数で混乱してしまったので、おうちで頭を整理します。
じっくり考えてみてください。
三角関数の微分も結局は微小変化のときのの変化量の話をしているのだとわかった。
微分というのは、全部それです。

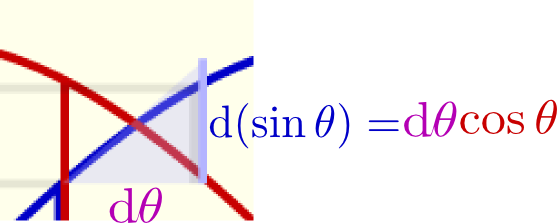 のように傾きが表示してある。この「傾き」が確かにcosθに比例していることを確認しよう。
のように傾きが表示してある。この「傾き」が確かにcosθに比例していることを確認しよう。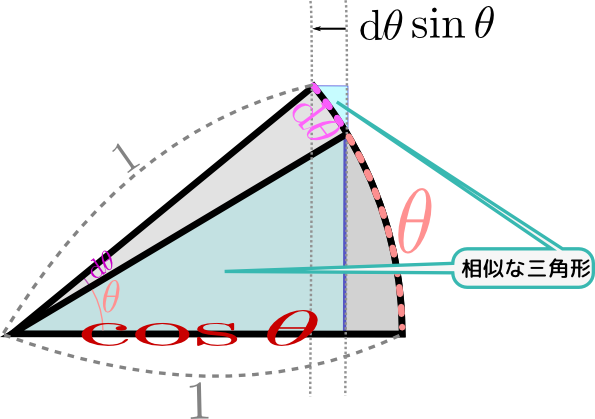

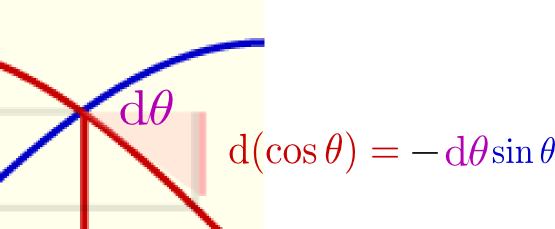 のように表示されている。これも動径をドラッグすることができるので、動かしながら「
のように表示されている。これも動径をドラッグすることができるので、動かしながら「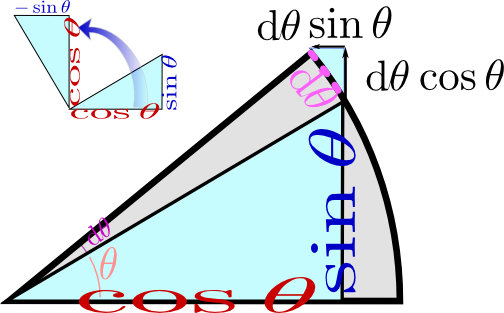
 のように、$x$座標を$y$座標に、$y$座標を(符号を変えて)$x$座標にすることで得られる。式で書くなら$(x,y)\to(-y,x)$であるが、これが微分$(\cos \theta,\sin \theta)\to(-\sin \theta,\cos \theta)$と同じ計算になっているわけである
のように、$x$座標を$y$座標に、$y$座標を(符号を変えて)$x$座標にすることで得られる。式で書くなら$(x,y)\to(-y,x)$であるが、これが微分$(\cos \theta,\sin \theta)\to(-\sin \theta,\cos \theta)$と同じ計算になっているわけである