青字は受講者からの声、赤字は前野よりの返答です。
主なもの、代表的なもののみについて記し、回答しています。
タブレットの時間20分ずれてます。
実は時間は全く、合わせてません(^_^;)。というわけでずれてても気にしないでください。
タブレットを使う授業は始めてで、グラフを自分の手で動かせるのでわかりやすかった(同様の関数多数)。
これからも使っていきます。
$n$次関数の$n$が400を超えると変化が見れないぐらい微妙だった。
そこまでいくともうあまり差がわからないでしょうね。
タブレットでグラフが動くとわかりやすくていいなと思ったんですが、$y=x^n$で$n$が1000以上まで行く機能はいらないなと思いました。
確かに、いらないですねぇ(←つけたのは私だけど)。
$n$次関数のものは、1498乗以降グラフが消えました。
その辺でコンピュータが計算できなくなったかな。
関数の見方が変わった。今まではただのグラフとしか見てなかったが、今は1次は傾きを表し、2次は曲がり具合を表しているのが理解できる。
その二つはこれからもとても大事です。」
$n$を大きくしたら($n\to\infty$)、グラフが
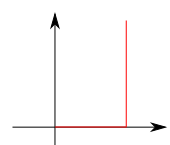
になりそう。
なるでしょうねぇ。
$y=x^n$の変化のしかたがおもしろいと思った。$y=ax^2+bx+c$の形も、$b$の変化での動き方などなじみのある関数でも新しい発見がたくさんあっておもしろかった。
変化を頭でイメージしましょう。
白菜にキムチすり込むのは朝がいいですか?夜がいいですか?
う〜ん、料理しないからわからないです。
質問したくなったがすぐに聞いていきます。
そうしてください、お願いします。
2次関数の1次の項の係数の意味は考えたことがなかったがおもしろかった(同様の関数多数)。
実は、深〜〜〜い意味があります。
自分は数学が苦手です。それはなぜかというと公式を覚えるのが難しいからです。でも今日、覚えるのじゃなくて理解して、使えるようであればいいと聞いて、少し自分でもできると思えることができました。
「おぼえる」のは勉強ではないので、「なぜ」と「どう使うか」を理解していきましょう。
クーラーの温度下げてください(同主旨多数)
私は授業中はしゃべることしか考えてないんで、下げたいなら勝手に下げてください。
タブレットの授業は始めてですが、自分でグラフを動かすのは楽しかった(同様の感想多数)。
楽しみながら、数学してください。
原点付近を考えるときは次数が少ない関数を重視することがわかった。
それ、とても大事な考えです。
先生関西の人ですか?
神戸生まれです。
はじめの様々な関数のグラフのページで、logならlogのグラフが出てきますが、この線を消すことができた方が学ぶときに有益だと重ます。というのも既にグラフの全貌がわかっていると$x$を動かしてそれに対応する$y$の値が動くという関数の本質がわかりずらく、ただレール上を動いているだけだと感じる学生もいるかと…。
うーん、なるほど。でも今の場合「関数」は最初から自分で選んでいますので。実は後でやる微分方程式のプログラムでは、少しずつ関数が現れるようになってます。
 を動かしてxを変化させると、それに応じて
を動かしてxを変化させると、それに応じて つまりyが動く。yの方は動かせません。「従属」変数ですから。
つまりyが動く。yの方は動かせません。「従属」変数ですから。 になったり、こう
になったり、こう なったしてます。
なったしてます。 になりそう。
になりそう。