テイラー展開
高階微分について振り返る
まず、androidアプリにした(←このボタンを押すとそのページに移動)で、高階微分の意味の雰囲気をもう一度思い出した。大事なことは、
- 一階微分は傾きであること。
- 二階微分は曲がり具合であること。
- 微分の階数が上がるほど、「近傍での寄与」は小さくなること(高階微分は「遠く」で効く)。
関数の近似
近似とはすなわち「真実の値とは少し違うが、だいたい等しい数値を求める」という方法である。
と、思う人が多い。「科学ともあろうものが『だいたい』なんていいかげんなことでよいのか?」と憤慨する人もいる。しかし、実際にはいろんな理由で近似が必要となる。まず、
ということが大きい。高校までの勉強では(大学でも低学年でなら)ほぼ、「解ける問題」しか出てこない。ところが世の中には「解けない問題」はいくらでもある。高校および大学初年度程度の教科書は「解ける問題」を厳選して載せている。では解けない問題が出てきたらどうするかと言えば、「頑張って解く方法を見つける(見つからないかもしれない)」か、「近似してから解く」しかない。
もう1つここで言っておきたいことは、真面目に解くことはほんとに必要か?ということである。たとえば(あくまで「たとえば」)近似しないで真面目に解いた場合の答と、近似した結果の答が0.1%(つまり$\textstyle {1\over 1000}$ぐらい)違っていたとしよう。その$\textstyle {1\over 1000}$の違いが大きな問題になる時もあれば、そうでない時もある。たとえば今最小目盛りが1mmである物差しで20cmぐらいの長さを測定したとしたら、この測定では$\textstyle {1\over 200}$より細かい精度の数字は得られていない。そういう測定で「近似したら$\textstyle{1\over 1000}$ぐらい答がずれる!」にこだわることは果たして必要だろうか?---近似してよいかまずいかは、要求されている精度によって決まるものである。要求される精度を十分に保つ近似に対して、近似だからといって文句を言われる筋合いはない。
関数近似の簡単な方法が「線形近似(linear approximation)」である。「線形(linear)」この場合に限らず、1次式で書けるという性質を「線形」と表す。英語から「リニア」という言い方もする。というのは「グラフで書くと直線になる」という意味で、($\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\ycol{y}=a\xcol{x}+b$のような)1次式で書けることである(微分のところでは「微小な範囲を考える(グラフを拡大する)」ことで線形近似できる形に持っていった)。
微分というのはいろんな関数$\ycol{y}=f\kakko{\xcol{x}}$を「拡大してみれば(あるいは、狭い範囲だけに注目すれば)直線$\ycol{y}=a\xcol{x}+b$のようなものだ」と大まかな近似として表した時の傾き$a$である、と言える。
微分の表現:$\kuro{f\kakko{\xcol{x} + \xcol{\Delta x}}\simeq f\kakko{\xcol{x}}+ f'\kakko{\xcol{x}}\xcol{\Delta x}}$を思い出し、$\xcol{x}\to x_0,\xcol{\Delta x}\to \xcol{x}-x_0$と置き直すと、 \begin{equation} f\kakko{\xcol{x}}\simeq f\kakko{x_0}+\left( \ddx f\kakko{x_0}\right)(\xcol{x}-x_0) \end{equation} ということになるこの$\ddx f\kakko{x_0}$は「関数$f\kakko{\xcol{x}}$を$\xcol{x}$で微分した後に$\xcol{x}$に$x_0$を代入したもの」という意味である(先に代入してしまったら微分すると0である)。すでに代入が終わっているので、この後$\xcol{x}$で微分すると0になる。釈然としない人がいるかもしれないが、これはそういう書き方をするのが(式を簡単に書くための)決め事なのだと思ってほしい。。この式は$\xcol{x}=x_0$を代入すると$f\kakko{x_0}=f\kakko{x_0}$となって成り立つし、$\xcol{x}$で微分してから$\xcol{x}=x_0$を代入しても成り立つ。しかしこれだと、$\xcol{x}$で二階微分すると等式は成り立たない(右辺は0になってしまうが左辺はそうとは限らない)。
授業ではここで「じゃあ二階微分も等しくするにはどうすればいいか考えてみよう」という時間を取った。ある程度1人で考えた後で、「では、隣近所で見せ合って議論して」という時間も設けた。
見ていると、
- $f''(x_0)(\xcol{x}-x_0)^2$を足す。
- ${1\over2}f''(x_0)\xcol{x}^2$を足す。
- ${1\over2}f''(x_0)(\xcol{x}-x_0)^2$を足す。
などの答が出ていた。
$\kuro{f''(x_0)(\xcol{x}-x_0)^2}$では二階微分したときに余計な2が出る。$\kuro{{1\over2}f''(x_0)\xcol{x}^2}$では二階微分はOKだが、一階微分が前と違ってしまう。$\kuro{{1\over2}f''(x_0)(\xcol{x}-x_0)^2}$にしておくと、この項の一階微分は$\kuro{f''(x_0)(\xcol{x}-x_0)}$で、$\kuro{\xcol{x}=x_0}$では消えるので問題ない。よって、正解は下の通り。
\begin{equation} f\kakko{\xcol{x}}\simeq f\kakko{x_0}+\left( \ddx f\kakko{x_0}\right)(\xcol{x}-x_0)+{1\over 2}\left( \left(\ddx\right)^2 f\kakko{x_0}\right)(\xcol{x}-x_0)^2 \end{equation} と新しい項を付け加えることで二階微分も等しくする。右辺を二階微分すると、第1項と第2項は0になり、第3項の${1\over 2}(\xcol{x}-x_0)^2$の二階微分は1になるので、結果は$\left(\ddx\right)^2f\kakko{x_0}$となり$\left(\ddx\right)^2f\kakko{x_0}$は「微分した後$\xcol{x}=x_0$を代入した結果」なのでもう$\xcol{x}$の関数ではないことに注意。、左辺の二階微分の$\xcol{x}=x_0$での値と一致する(こうなるように${1\over 2}$という係数を選んでおいた)。
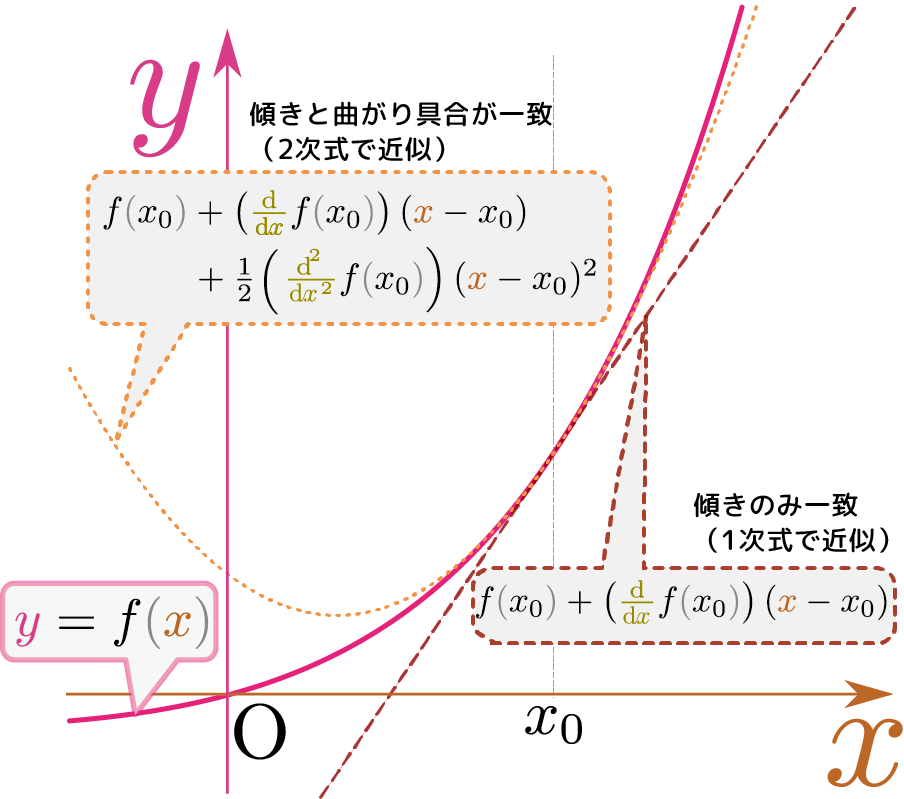
関数の値(零階微分)と一階微分、二階微分が一致するのだから、より本当の関数に近づいている(ここまでで「関数$f\kakko{\xcol{x}}$を2次式で近似する」ということができた)。この要領でどんどん右辺を左辺に近づけていく。この次の段階では、三階微分が等しくなるように、右辺に${1\over 3\times 2}\left(\left(\ddx\right)^3f\kakko{x_0}\right)(\xcol{x}-x_0)^3$を足す。以下同様に考えて、左辺と右辺で$\xcol{x}=x_0$での値$f\kakko{x_0}$と任意の階数の導関数$\left(\ddx\right)^nf\kakko{x_0}$が一致するようにすると、「テイラー展開(Taylor expansion)」と呼ばれる特に$x_0=0$の場合には「マクローリン展開」という別の名前がついているが、わざわざ別の名前にするほどの意味はない。、以下の式を作ることができる。
テイラー展開
\begin{equation} f\kakko{\xcol{x}}= \sum_{n=0}^\infty {1\over n!}\left(\left(\ddx\right)^nf\kakko{x_0}\right)(\xcol{x}-x_0)^n\label{taylorexp} \end{equation}ここで、$n=0$の項に$0!$が現れているが、$0!=1$である。$a^0$のときと同様に$0!=0$じゃないの?と不思議に思う人が多い。しかし、$n\times (n-1)!=n!$という「公式」が$n=1$の時にも成り立つべし、と考えると、$1\times(1-1)!=1!$となるので、$0!=1$と定義した方がよい。
以上の計算が実行できるような関数は$\xcol{x}=x_0$において「解析的(analytic)」であると言う。解析的であるためには、ある領域で何回でも微分可能という条件が成り立たなくてはいけない(さらに級数が収束$\sum_{n=0}^\infty$のような足算(これを「級数」と呼ぶ)の結果が特定の値に収まる(計算可能である)ことを「収束する」と表現する。収束しない場合を「発散する」と表現する。することも必要)。テイラー展開はこの条件のもとで考えている。このような「何回でも微分可能な関数」のことは「なめらかな関数」と呼ぶ。
テイラー展開の例:等比級数になる例
テイラー展開の例として、${1\over 1-\xcol{x}}$という関数のテイラー展開を考えよう。なぜこれを考えるかというと、この関数の「ある条件の元での展開」は微分を使わなくても出せる(よって、後で微分を使って出した展開式と比較できる)からである。というのは初項1、公比$\xcol{x}$の等比数列の和は \begin{equation} {1-\xcol{x}^{N}\over 1-\xcol{x}}= 1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\xcol{x}^4+\xcol{x}^5+\cdots+\xcol{x}^{N-1}=\sum_{n=0}^{N-1} \xcol{x}^n\label{touhix} \end{equation} になるという公式がある$( 1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\cdots+\xcol{x}^{N-1})(1-\xcol{x})$を計算すれば、$1-\xcol{x}^N$になることから導ける。。この式は \begin{equation} {1\over 1-\xcol{x}}=1+\xcol{x}+\xcol{x}^2+\cdots + \xcol{x}^{N-1} + \underbrace{ {\xcol{x}^N\over 1-\xcol{x}} }_{剰余項}\label{oneoverjouyo} \end{equation} と表すこともできる。「剰余項」と示した部分は、${1\over 1-\xcol{x}}-{1-\xcol{x}^N\over 1-\xcol{x}}$という計算の結果である。
$|\xcol{x}|<1$であれば、$\lim_{N\to\infty}\xcol{x}^N=0$になるから、$N$を$\infty$にすることで、 \begin{equation} {1\over 1-\xcol{x}}= 1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\xcol{x}^4+\xcol{x}^5+\cdots=\sum_{n=0}^\infty \xcol{x}^n\label{oneminux} \end{equation} を得る。この式はテイラー展開の式\式{taylorexp}の形になっている。というのは、 \begin{equation} \ddx \left({1\over 1-\xcol{x}}\right)={1\over (1-\xcol{x})^2},~~~ \ddx \left({1\over (1-\xcol{x})^2}\right)={2\over (1-\xcol{x})^3},~~~ \ddx \left({2\over (1-\xcol{x})^2}\right)={2\times 3\over (1-\xcol{x})^4},\cdots \end{equation} のように順に計算していくと \begin{equation} \left(\ddx \right)^n \left({1\over 1-\xcol{x}} \right)= n! \left({1\over 1-\xcol{x}}\right)^{n+1}\label{tayloronex} \end{equation} であることがわかり、この式に$\xcol{x}=0$を代入すると答えは$n!$となり、テイラー展開の公式\式{taylorexp}に入れれば${1\over 1-\xcol{x}}=\sum_{n=0}^\infty \xcol{x}^n$という式が成立するからである。ところが、上で$N\to\infty$の極限を取ったときに$\xcol{x}^N\to0$となるのは(級数の和を${1\over 1-\xcol{x}}$にできるのは)$|\xcol{x}|<1$の時だけである。つまりこの式が成立するのは、$-1<\xcol{x}<1$という範囲だけなのだ。
ここで、アプリを実行してテイラー展開により関数が近似される様子を見た。
しかし、この「近づいていく」という計算は、$-1<\xcol{x}<1$の範囲から離れてしまうともはや正しくない。$\xcol{x}=1$が「ここを超えるとテイラー展開できない点」になるのは考えてみればあたりまえで、そもそもテイラー展開の式は一階微分から初めて$n$階微分による影響を計算していくことで関数の値を求めようというものであるが、$\xcol{x}=1$のところで関数$f\kakko{\xcol{x}}={1\over 1-\xcol{x}}$は定義されておらず不連続で微分もできないから、「微分を使って値を求める」という計算であるテイラー展開が破綻するのは当たり前である「公式や定理は適用限界を超えて使ってはならない」を教訓として心に刻んでおこう。運良くそれでも大丈夫な場合もあるかもしれないが、確認は必要である。。実際、$\xcol{x}>1$の範囲では${1\over 1-\xcol{x}}$は負にならなくてはいけないが、$1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\xcol{x}^4+\xcol{x}^5+\cdots$は正にしかなりえず、この範囲では負の値を採っている${1\over 1-\xcol{x}}$に近づくことはない。
一方、$1+\xcol{x}+\xcol{x}^2+\xcol{x}^3+\xcol{x}^4+\xcol{x}^5+\cdots$という式は$\xcol{x}=-1$の時は \begin{equation} \underbrace{\underbrace{1-1+1-1+1-1}_{ここまでの和は0}+1}_{ここまでの和は1}-1+1-1+1-1+\cdots \end{equation} のような式となり、奇数個の項があると答は1、偶数個の項があると答は0、と$1$と$0$を振動している(グラフを見てもわかる)。一方、大本の${1\over 1-\xcol{x}}$は$\xcol{x}=-1$ではその中間である${1\over 2}$になる。
これは$1-1+1-1+1-1+1-1+1-1+\cdots={1\over 2}$と主張しているのではない。むしろ「こんなふうに無限和を計算してはダメ」と主張している。後で説明する収束半径を考慮しない計算だからである。
ここでもう一度前に出した式の剰余項の分子に$\xcol{x}^N$があることに注目して欲しい。剰余項の部分が$N\to\infty$で消えてしまうような状況になっていないと、ここで考えた展開は正しい展開にはなっていなかった(だから、$|\xcol{x}|<1$が必要だったのである)。
テイラー展開は、「どの範囲までが展開可能なのか」を正しく判断しないと間違えた展開の仕方をしてしまうことに注意しよう。
同じ式${1\over 1-\xcol{x}}$を、$\xcol{x}=0$ではなく$\xcol{x}=2$の周りでテイラー展開する。 \begin{equation} {1\over 1-\xcol{x}}=\sum_{n=0}^\infty {1\over n!}\underbrace{\left(\left(\!\ddx \!\right)^n \left({1\over 1-\xcol{x}}\right)\right)}_{n!\left({1\over 1-\xcol{x}}\right)^{n+1}}\biggr|_{\xcol{x}=2} (\xcol{x}-2)^n \end{equation} となるのでこれを計算すると、 \begin{equation} {1\over 1-\xcol{x}}=\sum_{n=0}^\infty (-1)^{n+1} (\xcol{x}-2)^n\label{sumxn} \end{equation} という、展開式ができる。
上でリンクしたアプリは展開点を変えることができるので、やってみよう。
この級数を$(\xcol{x}-2)$の$n$次まで足すことにすると、次のページのグラフに示したように、足す次数が上がるごとに線は${1\over 1-\xcol{x}}$に近づいていく。ただし、近づいていくのは$1<\xcol{x}<3$(つまり$|\xcol{x}-2|<1$)という範囲内だけである($\xcol{x}\geq 3$では激しく振動してしまうし、$\xcol{x}<1$では全く近づかない$\xcol{x}=1$はそもそも定義されてない。)。
このように、テイラー展開には有効な範囲がある。テイラー展開の中心から「テイラー展開できなくなる値」までの距離を「収束半径」と呼ぶ$\xcol{x}$という一次元量を扱っているので「半径」というのは変なのだが、そういう呼び方をすることになっている。。
冪級数が$\sum_{n=0}^\infty a_n (\xcol{x}-x_0)^n$という形で書かれている時、 \begin{equation} \lim_{n\to\infty}{1\over \sqrt[n]{|a_n|}},~~\lim_{n\to\infty}\left|{a_n\over a_{n+1}}\right|\label{shusokuhankei} \end{equation} のどちらかが存在していれば、それが収束半径になることがわかっている。
上の場合、$|a_n|=1$だから収束半径は確かに1である。
テイラー展開の例:指数関数
指数関数$\ycol{y}=\E^{\xcol{x}}$の場合は、微分しても微分しても$\E^{\xcol{x}}$のままであり、$\xcol{x}=0$での値は1だから、$\left(\ddx\right)^n f\kakko{x_0}$のすべてに1を代入して、 \begin{equation} \E^{\xcol{x}}=\sum_{n=0}^\infty {1\over n!}\xcol{x}^n =1+\xcol{x}+{\xcol{x}^2\over 2!}+{\xcol{x}^3\over 3!}+{\xcol{x}^4\over 4!}+{\xcol{x}^5\over 5!}+\cdots =\sum_{n=0}^{\infty}{1\over n!}\xcol{x}^n\label{exptaylor} \end{equation}
というテイラー展開になる(この式は前に「微分しても変わらない関数」として求めた)。
指数関数の場合、$a_n={1\over n!}$だから、$\left|{a_n\over a_{n+1}}\right|$は$n+1$となり、$n\to\infty$で$\infty$だから指数関数のテイラー展開の収束半径は$\infty$である。すなわち展開式は$\xcol{x}$の全ての範囲で正しい。
ここで、を実行してテイラー展開により関数が近似される様子を見た。