テイラー展開（続き）

$\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}$

三角関数のテイラー展開

　$\sin \xcol{x}$を例にして考えよう。すでに述べたように、$\sin \xcol{x}$は$\xcol{x}=0$で0であり、傾き1である。よって$\sin \xcol{x} \fallingdotseq \xcol{x}$と書けるのであった。$\sin \xcol{x}$の一階微分は$\cos \xcol{x}$、二階微分は$-\sin \xcol{x}$である。三階微分は$-\cos \xcol{x}$となり、微分するごとに$\sin \xcol{x}\to\cos\xcol{x}\to -\sin\xcol{x}\to -\cos\xcol{x}\to \sin \xcol{x}$と４つの関数をぐるぐる回る。

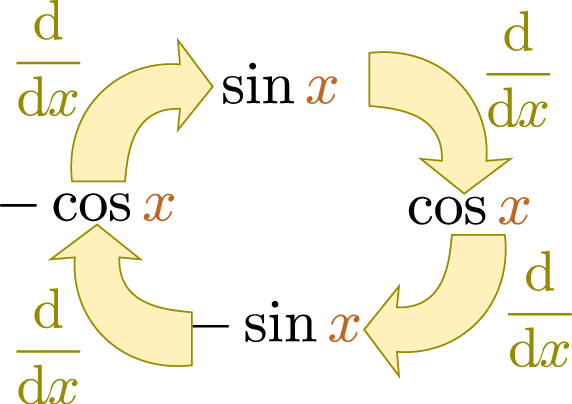
　分類すれば、 \begin{equation} \left(\ddx\right)^n \sin \xcol{x}= \begin{cases} \sin\xcol{x}& n=4m\\ \cos\xcol{x}& n=4m+1\\ -\sin\xcol{x}& n=4m+2\\ -\cos\xcol{x}& n=4m+3 \end{cases}~~~(mは0以上の整数)\label{sindiffn} \end{equation} であり、これに$\xcol{x}=0$を代入すれば \begin{equation} \left(\ddx\right)^n \sin \xcol{x} \biggr|_{\xcol{x}=0}= \begin{cases} 0& n=2m\\ 1& n=4m+1\\ -1& n=4m+3 \end{cases}~~~(mは0以上の整数)\label{sinexpcof} \end{equation} （$n=4m$と$n=4m+2$は一つにまとめて$n=2m$とした）であるから、 \begin{equation} \sin \xcol{x}=\xcol{x} - {\xcol{x}^3\over 3!}+ {\xcol{x}^5\over 5!}-{\xcol{x}^7\over 7!}+\cdots\label{sintaylor} \end{equation} のようにテイラー展開できる偶数次の項が出てこないのが$\sin$の特徴であるが、$\sin$に限らず奇関数なら常に奇数次しか出てこない。ただし、$\xcol{x}=0$以外で展開した場合はこの限りではない。。

　テイラー展開が近づいていく様子は、アプリを参照せよ。

一方、同様の計算をやると$\cos\xcol{x}$の方は \begin{equation} \cos \xcol{x}=1 - {\xcol{x}^2\over 2!}+ {\xcol{x}^4\over 4!}-{\xcol{x}^6\over 6!}+\cdots\label{costaylor} \end{equation} のようにテイラー展開できる（$\cos$では奇数次の項が出てこない偶関数のテイラー展開では常に、偶数次の項のみが出てくる。）。

　テイラー展開が近づいていく様子は、アプリを参照せよ。

　$\exp$の展開と、$\sin $の展開式と$\cos $の展開式をよく見ると、 \begin{equation} \begin{array}{ccccccccc} \E^{\xcol{x}}= &1 &+\xcol{x} &+{\xcol{x}^2\over 2!} &+{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+{\xcol{x}^5\over 5!} &+{\xcol{x}^6\over 6!} &+\cdots \\[3mm] \cos \xcol{x}= &1 & &-{\xcol{x}^2\over 2!} & &+{\xcol{x}^4\over 4!} & &-{\xcol{x}^6\over 6!} &+\cdots \\ \sin \xcol{x}= & &\xcol{x} & &-{\xcol{x}^3\over 3!} & &+{\xcol{x}^5\over 5!} & &+\cdots \\ \end{array}\label{Eulercossin} \end{equation} となっている。ここで「$\cos\xcol{x}$と$\sin\xcol{x}$の展開は$\E^{\xcol{x}}$に似ているが、符号が一項ごとに反転するのが惜しいな」と気づく。$\E^{\xcol{x}}$の展開で2項ごとに符号が反転してくれれば同じものになりそうだ。そうするためには、 \begin{equation} \begin{array}{cccccccccl} \E^{\xcol{x}}= &1 &+\xcol{x} &+{\xcol{x}^2\over 2!} &+{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+{\xcol{x}^5\over 5!} &+{\xcol{x}^6\over 6!} &+\cdots &~~~~~{\xcol{x}\to \I\xcol{x}と置き換えて}\\[3mm] \E^{\I \xcol{x}}=& 1 &+\I \xcol{x} &-{\xcol{x}^2\over 2!} &-\I{\xcol{x}^3\over 3!} &+{\xcol{x}^4\over 4!} &+\I{\xcol{x}^5\over 5!} &-{\xcol{x}^6\over 6!} &+\cdots \end{array} \end{equation} のように指数に虚数単位$\I$をつければよい（$\xcol{x}\to\I\xcol{x}$と置き換えればよい）と気がつけば、 \begin{equation} \E^{\I \xcol{x}}=\cos \xcol{x}+\I \sin \xcol{x}\label{Euler} \end{equation} という「オイラーの関係式」が見えてくる。

テイラー展開可能な点と不可能な点

　テイラー展開が可能であるためには、$f\kakko{x_0}$はもちろん、任意の階数の微係数$\ddx f\kakko{x_0},\left(\ddx\right)^2f\kakko{x_0},\cdots$が全て計算できなくてはいけない。たとえば、$f\kakko{\xcol{x}}=\sqrt{\xcol{x}}$を$\xcol{x}=0$の回りにテイラー展開することはできない（この関数は$\xcol{x}=0$において解析的でない）。$\ddx f\kakko{\xcol{x}}={1\over 2\sqrt{\xcol{x}}}$なので、$\xcol{x}=0$では微分が存在しない（あえて書くなら$\infty$）。グラフでは、$\xcol{x}=0$において線が垂直に立っていることで「微分できない」ことが表現されている。

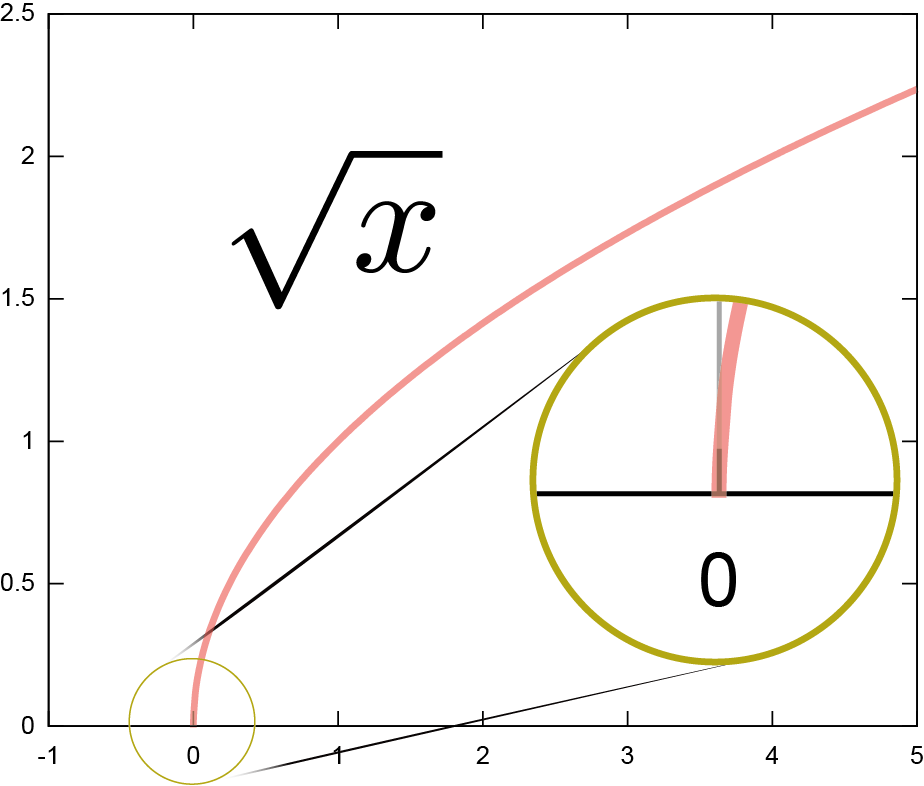
　では$\sqrt{\xcol{x}}$のような関数はどうやって近似するかというと、$\xcol{x}=0$以外、たとえば$\xcol{x}=1$の回りにテイラー展開する。$\xcol{x}=1$でなら、${1\over 2\sqrt{\xcol{x}}}\biggr|_{\xcol{x}=1}={1\over 2}$となって値がある。二階微分も計算しておくと、$\left(\ddx\right)^2\sqrt{\xcol{x}}=-{1\over 4\xcol{x}^{3\over 2}}$となるから2次の項の係数は${1\over 2}\left(\ddx\right)^2\sqrt{\xcol{x}}\biggr|_{\xcol{x}=1}=-{1\over 8}$であり（3次以上の項については詳細は省くが同様の計算を行って）、 \begin{equation} \sqrt{\xcol{x}}= 1 +{1\over 2}(\xcol{x}-1)-{1\over 8}(\xcol{x}-1)^2+{1\over 16}(\xcol{x}-1)^3-{5\over 128}(\xcol{x}-1)^4+\cdots \end{equation} のように展開できる。たとえば電卓を叩けば$\sqrt{1.2}\fallingdotseq1.09544511501033\cdots$という式が出るが、電卓内部では上のような展開を使って計算される。やってみると、 \begin{equation} \sqrt{1.2}= \underbrace{\underbrace{\underbrace{\underbrace{1 +\underbrace{{1\over 2}(1.2-1)}_{0.1}}_{1.1}-\underbrace{{1\over 8}(1.2-1)^2}_{0.005}}_{1.095}+\underbrace{{1\over 16}(1.2-1)^3}_{0.0005}}_{1.0955}-\underbrace{{5\over 128}(1.2-1)^4}_{0.0000625}}_{1.0954375}+\cdots \end{equation} のようにして正しい値に近づいていく。アプリを参照せよ。

積分

　まず、アプリを実行して、積分のイメージをつかんだ。

無限小部分の和としての積分

グラフの面積：直線の例

　もっとも簡単な「直角三角形」から始めることにしよう。

　上の図のような三つの角が$(0,0)(x_0,0),(x_0,x_0)$である直角三角形の面積を考える。三角形をいきなり考えるのではなく、「階段状の図形」を考え、階段の段数を増やしていくことで三角形に近づけていくことを考えよう。

　階段の段数が増えていくに従い、階段図形はどんどん考えている三角形に近づいている。

　一般的な分割数$N$で作った階段状の図形を次の図のように考えよう（後で$N\to\infty$とする）。

　三角形が横幅${x_0\over N}$の長方形の和で表現されている（長方形の和は、三角形より少しだけ小さい）。 一番左の領域を「0番め」と数えて$\ncol{n}$番めの領域（右図で色を濃くした部分）の左端は$\xcol{x}=\ncol{n}{x_0\over N}$であり、その場所の「高さ」も$\ncol{n}{x_0\over N}$である（三角形の斜辺は$\ycol{y}=\xcol{x}$で表されている）。よって、この台形$\ncol{n}=0$のみ、台形ではなく三角形。の形をした領域「台形とわかっているなら台形の面積の公式を使え」と思うかもしれないが、今「三角形」という単純な例を示しているからそうなるのであって、もっと複雑な図形では台形ではない。ここではまず「考えている図形より小さいことが保証される面積」を考えている。にぴたりと収まる長方形の面積は$\ncol{n}{(x_0)^2\over N^2}$である。これを \begin{equation} \sum_{\ncol{n}=0}^{N-1}\ncol{n}{(x_0)^2\over N^2} ={(x_0)^2\over N^2} \sum_{\ncol{n}=1}^{N-1}\ncol{n} =(x_0)^2\times{N-1\over 2N}\label{NNN} \end{equation} のように$\ncol{n}=0$から$\ncol{n}=N-1$まで足す実は$\ncol{n}=0$の項は0なので、$\ncol{n}=1$から足しても同じこと。。ここで$\sum_{\ncol{n}=0}^{N-1}\ncol{n}={N(N-1)\over 2}$という和の公式を用いた。最後にある${N-1\over 2N}={1\over 2}-{1\over 2N}$という量は${1\over 2}$より${1\over 2N}$だけ小さい数だから、$N$をどんどん大きくしていけばこの部分が${1\over 2}$となり、長方形の集合の面積は${(x_0)^2\over 2}$、つまり${(底辺)\times(高さ)\over 2}$に下から近づいていく「より小さい」という大小関係を守りつつその値に近づいていく場合は「下から近づく」と表現する。逆の場合は「上から近づく」である。。これで、長方形の集合の面積$\leq{(底辺)\times(高さ)\over 2}$が証明正確には、$\leq$ではなく$<$が証明されている。そして、$N\to\infty$においてこれが$=$になるだろう、というのは今の段階だはまだ単なる「予想」でしかない。できた（まだ等式ではない）。

　そこで、長方形の作り方を少し変えてみる。具体的には上では「常に長方形が三角形の下にある」ようにした（こうして求めた面積を「下からの極限」と呼ぼう）が、「常に長方形が三角形より上に飛び出ている」ようにする（こちらは「上からの極限」と呼ぼう）。

　すると足すべきものが$\ncol{n}=1$から$\ncol{n}=N$までここは「$\ncol{n}=0$から$\ncol{n}=N-1$まで」のままで変えず、足算する量の$\ncol{n}\to \ncol{n}+1$と置き換えても同じこと。となり、 \begin{equation} \sum_{\ncol{n}=1}^{N}\ncol{n}{(x_0)^2\over N^2} ={(x_0)^2\over N^2}\underbrace{\sum_{\ncol{n}=1}^{N}\ncol{n}}_{{N(N+1)\over 2}} =(x_0)^2\times{N+1\over 2N} \end{equation} となる。今度は最後に${1\over 2}+{1\over 2N}$があり、これが$N\to\infty$で${1\over 2}$に上から近づく。よって、この極限の取り方（上からの極限）では、長方形の集合の面積$\geq{(底辺)\times(高さ)\over 2}$が証明でき、 \begin{equation} \left({下からの極限による\atop 長方形の集合の面積}\right)\leq{(底辺)\times(高さ)\over 2}\leq \left({上からの極限による\atop 長方形の集合の面積}\right) \end{equation} がわかった。二つの極限は一致するから、三角形の面積$={(底辺)\times(高さ)\over 2}$が示せた。

　ここで考えた二つの足算は「下からの極限」の方は微小な長方形（面積が$\xcol{x}\coldx$）の足算として、「上からの極限」の方は微小な長方形（面積が$(\xcol{x}+\coldx)\coldx$）の足算として計算されたことに注意しよう。そして最後の極限の結果は「$\xcol{x}$に$\coldx$を足したかどうか」に依らない。微小量の計算において$\Odr\kakko{\coldx^2}$が無視できたのは、こうして積分するときにその差が効いてこないからである。

　以下で、もっと一般的な関数（「一般的なグラフ」と言ってもいいし、「一般的な図形」と言ってもいいだろう）に対して同様の計算を行っていく。そこで少し記号を整理しよう。上で考えた${x_0\over N}$という微小長方形の横幅は「$\xcol{x}$の変化量で、後で0になる極限を取るもの」という意味を持っているから、微分の時と同様に、$\coldx$と書くことにしよう同じ意味を持つ量なので、同じ記号を使っている。積分で$\coldx$のような記号が登場するのは、意味のあることである。。$\xcol{x}=\ncol{n}{x_0\over N}$であることも使うと、三角形の面積は（面積が小さくなるように考えた場合）

\begin{equation} \sum_{\ncol{n}=1}^N \underbrace{\ncol{n}{x_0\over N}}_{\xcol{x}}\times \underbrace{{x_0\over N}}_{\coldx}=\sum_{\ncol{n}=1}^N\xcol{x}{\coldx}\label{xakadx} \end{equation} と書くことができる。

　$\xcol{x}\coldx$という部分は、「底辺$\coldx$、高さ$\xcol{x}$」の微小長方形の面積を意味しているこの$\coldx$は「$\xcol{x}$で積分しますよ」ということを伝えるためだけにある記号ではなく、積分が「関数の値（今の場合$\xcol{x}$）と微小変化（今の場合$\coldx$）の積を足す」という計算であることから来ている。。

　$N\to\infty$という極限は$\coldx\to0$という極限であり、その極限において今考えている和は「無限個の区間の足算」に変わる。

　$1$から$N$まで$\ncol{n}$を変化させつつ足すが$N\to\infty$（$\coldx\to0$）という極限を取ることによって、$0$から$x_0$まで$\xcol{x}$を変化させつつ足す（まさに「足算の化け物」）に変わったのだから、記号の方も$\sum_{\ncol{n}=1}^N$ではない別の記号$\int$の読み方は「いんてぐらる」。記号自体は「積分記号」と呼ぶ。元々は「和」に対応するラテン語（summa、英語のsummation）のsを伸ばして作られた（ライプニッツによる）。つまり、和の記号$\sum$と語源は同じということになる。$\int_0^{x_0}$を使うことにする。

　こうして新しい記号で書いた$\int_0^{x_0} \xcol{x}\coldx$が「定積分(definite integral )」という演算である（後で「不定積分」も出てくる）。この書き方では結果を \begin{equation} \int_0^{x_0}\xcol{x}\coldx={(x_0)^2\over 2}\label{sekibunx} \end{equation} と表すことができる。

　$\int_a^b$と書いた時の$a$は「（定積分の）下限」、$b$は「（定積分の）上限」と呼び「どこからどこまでを足したのか」を示す$\left(\int_{下限}^{上限}\right)$。領域$a<\xcol{x} < b$は「積分区間」と呼ぶ。上の例では$0,x_0$が下限と上限だったが、もちろんどこからどこまでを足すかは状況によって変わる。

定積分の記号についての整理

　定積分はもちろん、いろんな関数について実行できる。「$f\kakko{\xcol{x}}$という関数を$x_1$から$x_2$まで定積分する（つまりその範囲で$\xcol{x}$軸とグラフに挟まれた面積を計算する）」を式では$\int_{x_1}^{x_2} f\kakko{\xcol{x}}\coldx$と書く。$f\kakko{\xcol{x}}$は「被積分関数(integrand)」と呼ぶ。また、この時の変数は「積分変数」と呼ぶ。

　具体的には「$x_1$から$x_2$まで」という長さ$x_2-x_1$の領域を$N$分割し、その一個一個の微小領域（最初を「0番め」として、$\ncol{n}$番めの微小領域は$\xcol{x}=x_1+\ncol{n}{x_2-x_1\over N}$で始まる）に横${x_2-x_1\over N}$で縦$f\kakko{x_1+ \ncol{n}{x_2-x_1\over N}}$の微小長方形を作り、その面積の和を計算する。式で表現すれば \begin{equation} \underbrace{\lim_{N\to\infty}\sum_{\ncol{n}=0}^{N-1} }_{\displaystyle \int_{x_1}^{x_2}} \underbrace{f\kakko{x_1 + \ncol{n}{x_2-x_1\over N}}}_{\displaystyle f\kakko{\xcol{x}}}\underbrace{{x_2-x_1\over N}}_{\coldx} \end{equation} である。正確には、上に書いたような単純な極限ではなく、「下からの極限」と「上からの極限」になるようにしてから両方を計算した上で二つの極限が一致することを示さなくてはいけない。一致しない場合は「積分可能でない」関数だったということになる。

　この定義からわかるように、$f\kakko{\xcol{x}}$が負の領域での積分はマイナスの値になる。つまり定積分の結果は単純に面積ではなくグラフの線が$\xcol{x}$軸より下にあれば負にして計算する、「符号付き面積」である。

\begin{equation} \int_a^b f\kakko{\xcol{x}}\coldx + \int_b^c f\kakko{\xcol{x}}\coldx = \int_a^c f\kakko{\xcol{x}}\coldx\label{intsum} \end{equation} という式が成立するここで、$\xcol{x}=b$で二回同じものを足してはいないかと心配する人がいるかもしれないが、それは$\Odr\kakko{\Delta x}$の量だから結果には関係ない。。また、 \begin{equation} \int_a^b f\kakko{\xcol{x}}\coldx =- \int_b^a f\kakko{\xcol{x}}\coldx \label{hantaiint} \end{equation} すなわち、「上限と下限を取り替えると符号が変わる」という性質元々の「面積を計算したい」という動機だけから考えると、$a < b$の時に$\int_b^a f\kakko{\xcol{x}}\coldx$を考えるのはナンセンスに思えるかもしれない。しかし、数式を書く上での規則は、できる限り「例外がない」ものが望ましいので、イレギュラーに見える式も作っておけば後で役立つ（かもしれない）。も持つ。この式はどのような$a,b,c$でも成立する式であるべきだこれも「できる限り例外がない規則」が欲しいからである。から、$c=a$を代入すれば右辺が$\int_a^a f\kakko{\xcol{x}}\coldx=0$になることから導ける。これらを合わせて \begin{equation} \int_a^c f\kakko{\xcol{x}}\coldx - \int_a^b f\kakko{\xcol{x}}\coldx = \int_b^c f\kakko{\xcol{x}}\coldx\label{hikisanint} \end{equation} という式を作ることもできる（上の図をもう一度よく見るとわかる）。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。