微分方程式
微分方程式とは
「微分方程式(differential equation)」とは、独立変数$\xcol{x}$、従属変数$\ycol{y}$と、その微分$\ddx \ycol{y},\dtwodx\ycol{y},\cdots$の間にある \begin{equation} \Phi\left(\xcol{x},\ycol{y},\ddx \ycol{y},\dtwodx\ycol{y},\cdots\right)=0 \end{equation} のような形で書ける関係式($\Phi$は任意の関数)であり、この式を満たす$\ycol{y}$と$\xcol{x}$の関係を($\ycol{y}=f\kakko{\xcol{x}}$などのような形で)求めるのがその目的である。グラフで考えると一階微分$\ddx \ycol{y}$は傾きを、二階微分$\dtwodx\ycol{y}$は曲がり具合を表現している。つまり微分方程式は「ある場所$(\xcol{x},\ycol{y})$での局所的(local)な情報」の間の関係式である。一方、関数$\ycol{y}=f\kakko{\xcol{x}}$を与えると、二つの変数の間の関係を大域的(global)に与える。微分方程式を解くというのは局所的情報から大域的情報を導くことであるとも言える(逆に微分は、大域的情報から局所的情報を得る)。
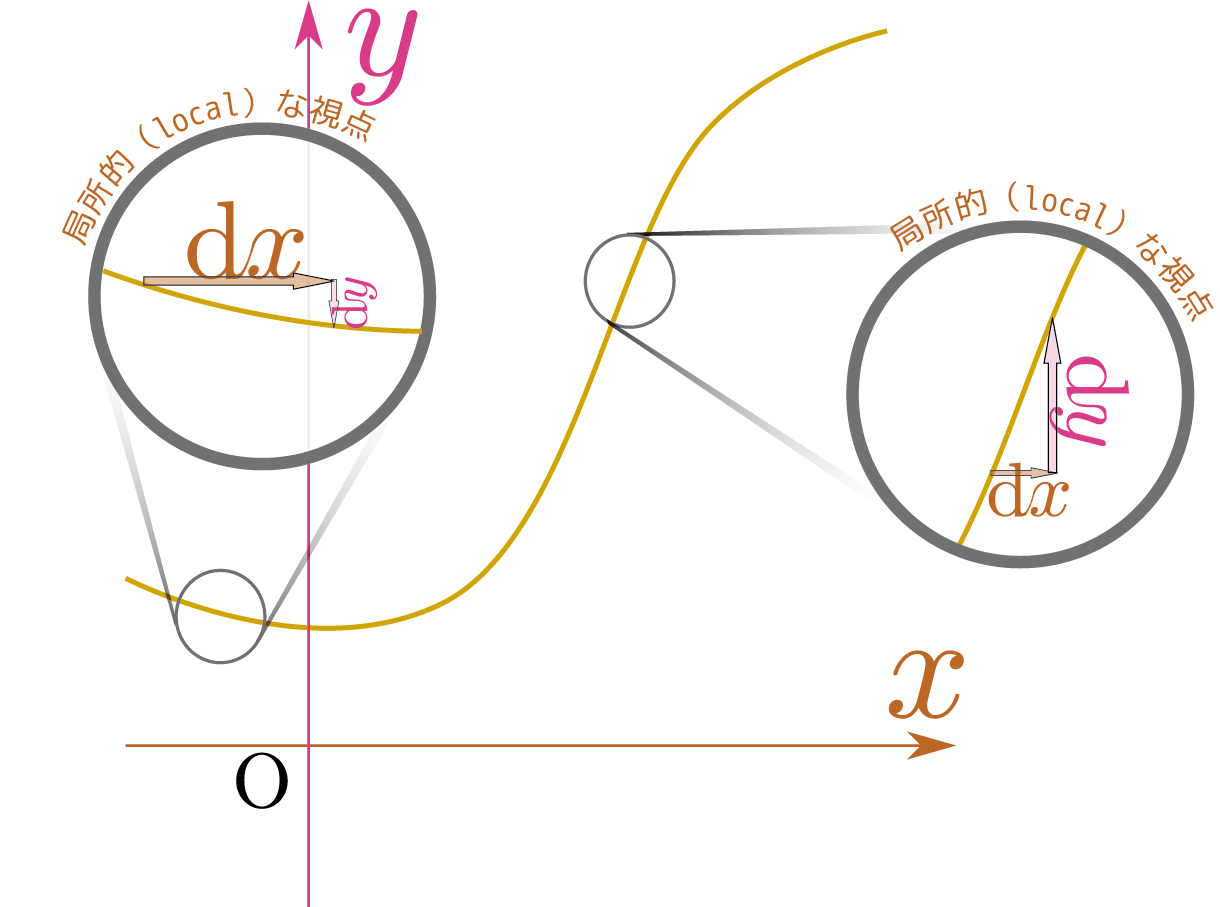
なぜこういう手法が有効なのかというと、自然を相手にした時、全部(つまり、大局的状況)をいっぺんに考える(globalに考える)ことが人間の手に余ることが多いからである。ゆえに我々は狭い領域(つまり、局所的状況)をまず考える(localに考える)ことにする。そしてその狭い領域での「法則」を見つけてから前に進む。この方法は物理などの自然科学でこれまで大きな成果(ニュートン力学、電磁気学、流体力学、みんなそう)を上げてきたのである。
簡単な微分方程式から
答が直線になる微分方程式
ある点において、傾きが1とはグラフにおいて右斜上45度の方向に線が伸びていくことである。そこで、この節の図ではこれを と表現することにしよう。
と表現することにしよう。
ここからしばらく${\coldy\over \coldx}=$なんとかの形の一階微分方程式を扱うが、この式の表すところは、
である。マーク を「この場所では右上45度の方向に進め」という命令と解釈しよう。「微分方程式の示す命令に従い進んでいけばどのような線ができあがるか」を考えるのが微分方程式を解くことである。
を「この場所では右上45度の方向に進め」という命令と解釈しよう。「微分方程式の示す命令に従い進んでいけばどのような線ができあがるか」を考えるのが微分方程式を解くことである。
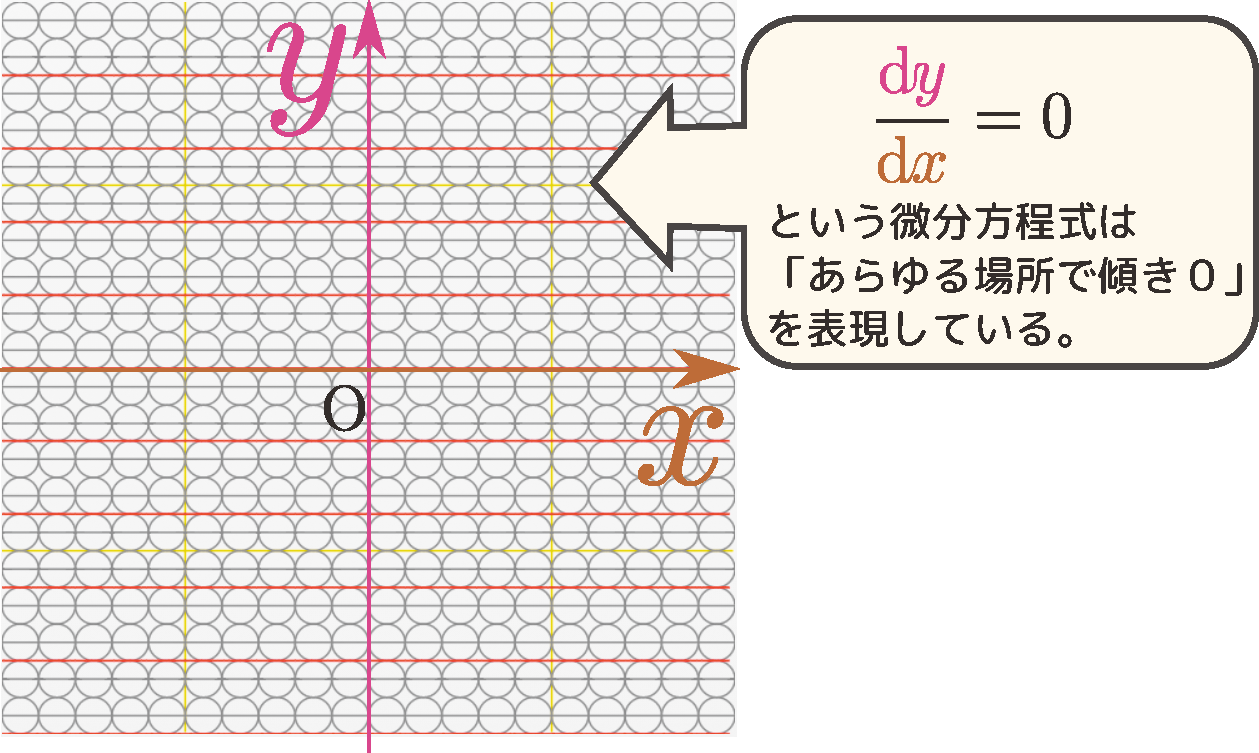
最も単純な微分方程式である
\begin{equation}
{\coldy\over\coldx}=0\label{DEzero}
\end{equation}
は「至るところで傾き0」を表す。その様子を表したのが右のグラフで、「傾き0」または「右に進め」もしくは「左に進め」 という命令を表す で埋め尽くされている。
で埋め尽くされている。
この方程式の解は計算するまでもない。 \begin{equation} \ycol{y}=C\label{DEzerosol} \end{equation} である(積分した結果が上の式だと考えても同じこと)。
FAQ:「方程式」を解いたのに、答がたくさん出てくるのですか?
そもそも「方程式を解く」というのは、「式の形で与えられた条件に合う『もの』を見つける」ということである。「二次方程式$\xcol{x}^2-4\xcol{x}-12=0$」ならば条件に合う『もの』は$\xcol{x}=6,-2$という二つの数だが、今解いている「微分方程式」の場合、解となる『もの』は数ではなく関数なのである。
微分方程式は、数式として表現すれば「微係数${\coldy\over \coldx}$」を決める式である。一方、図形で考えると、各点各点で、 だったり
だったり だったりという「グラフの傾き」を決めているのが微分方程式である。(これは「局所的な法則である」と言ってもいい)。 グラフの傾きだけ決めても、グラフ全体は「どこを通るか」を変えれば一般に変わる。微分方程式の答として線が得られるが、出発点が違っていれば結果としてできあがる線も違うものになってしまう。そのため、微分方程式の「解」は1つには決まらない。これは微分方程式の持つ、一般的な性質である。
だったりという「グラフの傾き」を決めているのが微分方程式である。(これは「局所的な法則である」と言ってもいい)。 グラフの傾きだけ決めても、グラフ全体は「どこを通るか」を変えれば一般に変わる。微分方程式の答として線が得られるが、出発点が違っていれば結果としてできあがる線も違うものになってしまう。そのため、微分方程式の「解」は1つには決まらない。これは微分方程式の持つ、一般的な性質である。
答えが放物線になる微分方程式
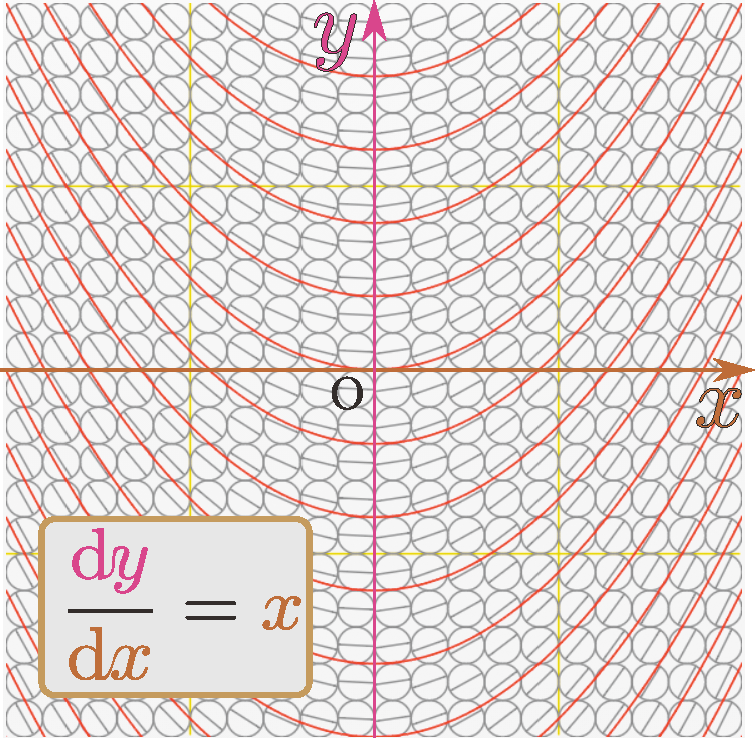
積分曲線が文字通り「曲線」になる例に行こう。${\coldy\over \coldx}=\xcol{x}$を考えてみる。この場合、$\xcol{x}$が大きくなると(グラフ上で右に行くと)傾きが大きくなっていく。こういう性質をもった量は自然科学にもよく登場するたとえばバネは伸び縮みに比例して力が強くなる。力はエネルギーの増加に比例するので、傾きが力に比例するとすれば、この$\ycol{y}$はエネルギーである。。
$\ycol{y}$軸の上では$\xcol{x}=0$だから、傾きも0(水平すなわち )となる(図では$\ycol{y}$軸の真上には○を描いていないが)。$\xcol{x}$が増加する(グラフ上で右に移動する)にしたがって傾きは増加していき、$\xcol{x}=1$の場所では傾きが1(図では
)となる(図では$\ycol{y}$軸の真上には○を描いていないが)。$\xcol{x}$が増加する(グラフ上で右に移動する)にしたがって傾きは増加していき、$\xcol{x}=1$の場所では傾きが1(図では )になる。
)になる。
また、\範囲{$\xcol{x}<0$}の領域に行くと傾きがマイナス(右下がり)になっていることもわかるであろう。
${\coldy\over \coldx}=\xcol{x}$という式を見たときに、以上のような図形的イメージを持って欲しい。
このグラフで各点各点をこの傾きで通るように線をつないでいくと$\ycol{y}={\xcol{x}^2\over 2}+C$で表される線、いわゆる放物線ができる。微分方程式${\coldy\over \coldx}=\xcol{x}$は、「ある場所で線がどっちを向いているか(ローカルな情報)」を表している。それから、解$\ycol{y}={\xcol{x}^2\over 2}+C$すなわち「どんな線か(グローバルな情報)」を導くというのが「微分方程式を解く」という作業なのである。
この中に答が「円」になる微分方程式があったので、以下の質問が出た。
答が指数関数となる微分方程式
これまでもでてきた \begin{equation} {\coldy\over\coldx} =\ycol{y}\label{dfdxf} \end{equation} も微分方程式である。この式の解の少なくとも一つである「微分すると$\ycol{y}$に戻る関数」を、我々はとっくに知っていて、 \begin{equation} \ycol{y}=\E^{\xcol{x}}\label{solex} \end{equation} がその答えであるが、これは「一つの解」であり「全ての解」ではない。
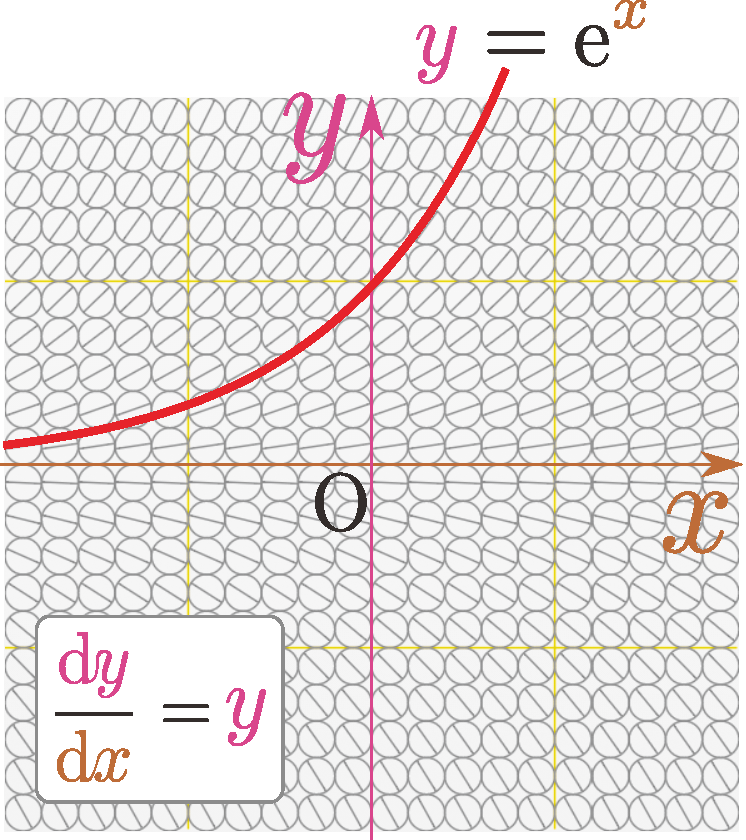
この式がグラフの傾きを決めているという立場に立って考えてみると、上のような「傾きの図」が描ける。図に示したのが、$\ycol{y}=\E^{\xcol{x}}$のグラフである。この線一本では、${\coldy\over \coldx}=\ycol{y}$を満たす線の全てが表現されていない。数式としての側面から「複数の解がある」ことを見てみよう。式をよく見ると、$\E^{\xcol{x}}$に定数$A$を掛けた$\ycol{y}=A\E^{\xcol{x}}$もまた、この微分方程式を満たすことがわかる。両辺が$f\kakko{\xcol{x}}$に関して1次式だからである一般に、微分方程式が求めるべき関数$\ycol{y}$に関して同次(1次なら1次ばかり、2次なら2次ばかりを含んでいる)ならば、定数倍しても解である。。ということは、任意の定数を$A$として \begin{equation} \ycol{y}=A\E^{\xcol{x}}\label{solgen} \end{equation} がすべて解となる。あらゆる$A$の値に対応する一つずつの$\ycol{y}$すべてが解である。
「一つの解」である$\ycol{y}=\E^{\xcol{x}}$を「特別な解」という意味で「特解(particular solution)」と呼ぶのに比べ、$\ycol{y}=A\E^{\xcol{x}}$という解を「一般解(general solution)」(これで微分方程式のすべての解を表現している、という意味で「一般」をつける「一般解」という用語の意味は少し混乱がある。後で述べる。)と呼ぶ。
一般解はたくさんあり(上の場合、$A$が変われば解が変わるから、無限個の解がある)、微分方程式だけでは一つに定まらない。解を一つに定めるためには、$\xcol{x}=0$で$\ycol{y}=1$とする(この場合$A=1$)のようになんらかの付加的な条件を置く。
このような条件は状況に応じて「境界条件(boundary condition)」あるいは「初期条件(initial condition)」などと呼ばれる条件を定める場所が時間的な「最初」である時に「初期条件」という言葉がよく選ばれる。。
指数関数が出てくる自然現象
このような方程式に従う自然現象の例に、放射性物質の崩壊がある。放射性物質は、「半減期」と呼ばれる一定期間(以下$T$とする)を経過すると元の量の${1\over 2}$が崩壊し、別の物質に変化する注意すべきは「半減期の2倍」の時間が経過すると全部なくなるのではなく、元の量の${1\over 4}$になる、ということ。。時刻$\tcol{t}$で残っている放射性物質の量は$N\kakko{\tcol{t}}=N\kakko{0}\left({1\over 2}\right)^{\tcol{t}\over T}$という、${\tcol{t}\over T}$が1増えるごとに${1\over 2}$になるという式で表される。ここで${1\over 2}=\E^{-\log 2}$を使って、 \begin{equation} N\kakko{\tcol{t}}=N\kakko{0}~\E^{-{\log 2\over T}\tcol{t}} \label{hangenki} \end{equation} と書く。これは言わば大局的な情報としての式である(そして、実験的にもよく確認された式であると言える)。では、この式にはどのような自然法則が隠れているだろうか。「微分」という作業がこの現象の局所的情報を取り出してくれる。
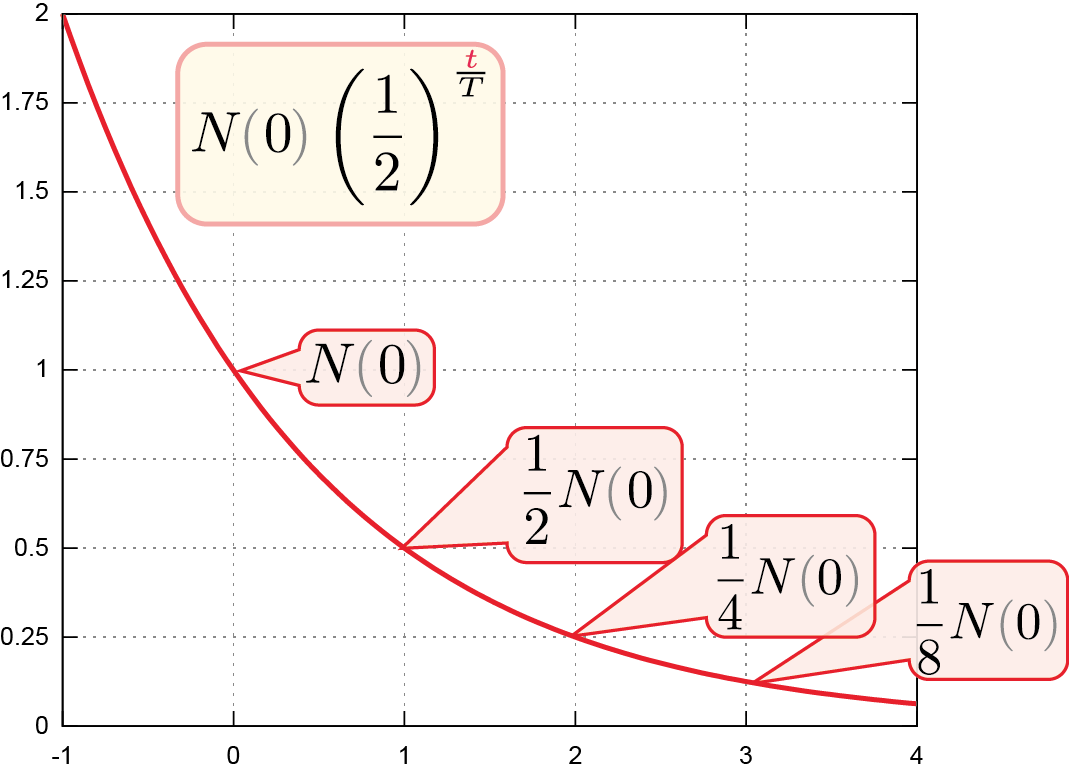
上の式を微分してみると、 \begin{equation} \begin{array}{c} {\diff \over \coldt}N\kakko{\tcol{t}}=-{\log2\over T} N\kakko{\tcol{t}} \\ ~~または~~\\ \ycol{\diff N}=-{\log2\over T}\ycol{N} \coldt \end{array} \end{equation} のように、${\coldy\over\coldx}=\ycol{y}$に似た式が出る違いは$\xcol{x}\to\tcol{t},\ycol{y}\to \ycol{N}$という変数の違いと、右辺に定数係数$-{\log2\over T}$がついていること。。
この式$\ycol{\diff N}=-{\log2\over T}\ycol{N} \coldt$は、微小時間$\coldt$の間に放射性物質の量が${\log 2\over T}\ycol{N}\coldt$だけ減ることを表す。すなわち、「今ある量に比例して減る」という法則を示している。ある一個の放射性物質の原子に着目すると、その原子はまわりの状況や物質の状態とは無関係に一定確率で崩壊するまわりの状況によって変化する確率が違ってくる場合は、また別の形の微分方程式が出てくる。。これが生物の死であれば「年老いた個体は死にやすい」「密集した環境では食料が確保できず死にやすい」などの理由で確率が変わる。原子には「年齢」のような個性がないこと、その崩壊が周りの環境に左右されないことなど(どちらも物理法則からくること)が、見えている現象としての崩壊の様子から逆算してわかる。逆にいえば、そういう性質を持っている物が起こす現象は、これと同様の微分方程式で記述できるだろう。
このように、微分方程式はある(空間的に、あるいは時間的に)狭い範囲で成り立つ法則を記述している。微分方程式を解くことは、「狭い範囲で成り立つ法則」から「広い範囲で成り立つ式」を作っていくことである。自然現象は複雑なものであり、それを一気に理解するのは人間の思考の範疇を超えている場合がある。そのようなとき、狭い範囲だけを見てまず「微小領域で成り立つ法則」を導き出すことで理解していこうというのが微分方程式を作り解いていくときの考え方である。自然科学を深く勉強していけば、この「まずは微小領域で考える」という考え方が、意外なほどに多くの場面で有効であることに気づくだろう。
答が直線になる微分方程式
ここで、原点を通る直線が出てくる微分方程式(アプリ「微分方程式を図解する」の中にあった)を考えよう。その微分方程式${\coldy\over \coldx}={\ycol{y}\over \xcol{x}}$がどのような傾きを表現しているかを図解しておこう。
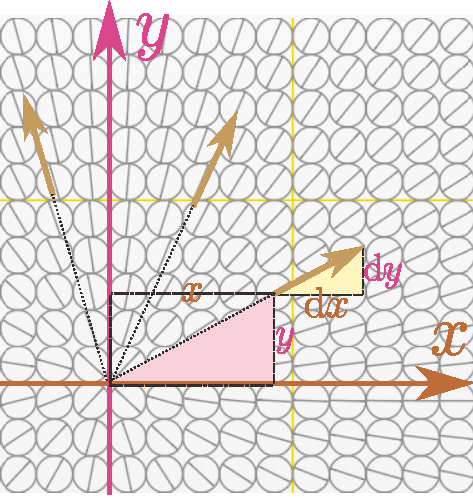
${\ycol{y}\over \xcol{x}}$というのは、図に書いた「原点から$(\xcol{x},\ycol{y})$へと引いた線」の傾きである。その傾きが、その場所$(\xcol{x},\ycol{y})$に引かれる線の傾きに一致する。つまり${\coldy\over \coldx}={\ycol{y}\over \xcol{x}}$は、考えている線に対し、「原点から自分のいる場所に引っ張った線と同じ方向に進め!」と「線を伸ばすルール」を決めている。
図で考えても式で考えても同じ結果が出るのはもちろんだが、${\coldy\over\coldx}$が複雑な式になればなるほど、「図を見て考える」は面倒になるたとえば台風の渦の形はなぜああなるのか、はこれよりもっと複雑な微分方程式を立てることで(ある程度)理解することができる。しかしそれは図だけで考えても、式を使って考えても大変だ。。だからこそ微分方程式を「数式で解く」ことが大事になる。
微分方程式の解に含まれるパラメータの数
上で述べたように、微分方程式の解には、微分方程式だけでは決まらないパラメータが必ず含まれる。それは微分方程式が局所的情報を表す式であることから必然的にもつ性質である。微分方程式を解く時にもこの点は大事なので、解が含むパラメータの数について考察しておこう。
${\coldy\over \coldx}=\ycol{y}$の解が$\ycol{y}=A\E^{\xcol{x}}$だったことを例として考えよう。
パラメータ$A$は変数分離を行った結果の${\coldy\over \ycol{y}}=\coldx$を積分するときの積分定数から現れる。具体的な積分結果は$\log\ycol{y}=\xcol{x}+C$${\coldy\over \coldx}=\ycol{y}$から${\coldy\over \ycol{y}}=\coldx$へと変数分離を行う際に「両辺を$\ycol{y}$で割る」という計算をやっているが$\ycol{y}=0$の場合、これは許されない。ここでは暗黙のうちに$\ycol{y}\neq0$を仮定している。であるが、$ \ycol{y}=\E^{\xcol{x}+C}=\E^C \E^{\xcol{x}}$となるから、$A=\E^C$である「この形だと$A$は負になれないのでは?」と心配する人もいるかもしれないが、$C$が$\I\pi$という虚部を持っていれば、$A$は負にもなるので気にしなくてよい。心配すべきは$A=0$なのだが、この場合はその点も大丈夫である。変数分離を行うときでは$\ycol{y}\neq0$が仮定されていたが、幸いなことに$\ycol{y}=0$はこの一般解$\ycol{y}=A\E^{\xcol{x}}$の、$A=0$の場合に含まれているので、$\ycol{y}\neq0$の条件は外してよい。。
FAQ:{$\log\ycol{y}=\xcol{x}+C$の左辺に積分定数はいらないのですか?
左辺に積分定数をつけても、結果は同じなのだ。もし左辺に積分定数をつけたとすれば、左辺の積分定数と右辺の積分定数は別の定数なのでそれをそれぞれ$A,B$として \begin{equation} \begin{array}{rl} \log\ycol{y}+A=&{\xcol{x}}+B \end{array} \end{equation} となるが、積分定数を右辺に寄せて$\log\ycol{y}={\xcol{x}}+B-A$とすることができる。こうすると、$A$も$B$もまだ決まっていない数であり、しかも結果には$B-A$という組み合わせでしか出てこない。つまり$B-A$だけを求めればよいから、$C=B-A$とおいて1つの積分定数と思えばよい(これを「$A$を$B$に吸収させる」と表現する)。
次に二階微分方程式の簡単な例$\left(\ddx\right)^2f\kakko{\xcol{x}}=\ddx f\kakko{\xcol{x}}$を同様に解いてみよう。 $$ \begin{array}{rll} \left(\ddx\right)^2f\kakko{\xcol{x}}=&\ddx f\kakko{\xcol{x}} &\kokode{両辺を不定積分} \\[-2mm] \end{array} $$
\begin{equation} \begin{array}{rll} \ddx f\kakko{\xcol{x}}=&f\kakko{\xcol{x}}+C&\kokode{f\kakko{\xcol{x}}+C=\ycol{y}と置く}\\[-2mm] \ddx (\ycol{y}-C)=& \ycol{y}&\kokode{\ddx(-C)=0を使って、さらに変数分離}\\[-2mm] {\coldy\over \ycol{y}}=& \coldx&\kokode{もう一度積分}\\[-2mm] \log \ycol{y}=& \xcol{x}+D&\kokode{\E の肩に乗せて}\\[-2mm] \ycol{y}=&\E^{\xcol{x}+D} \end{array}\label{simpleav} \end{equation}
こうして解は($f\kakko{\xcol{x}}$に戻して)$f\kakko{\xcol{x}}=-C + \E^{\xcol{x}+D}$または$f\kakko{\xcol{x}}=-C+D'\E^{\xcol{x}}$($D'=\E^D$)となり、積分を二度やった結果として積分定数$C,D$(または$C,D'$)の二つのパラメータが現れる。
微分方程式を解くとは積分すること、と考えると「$n$階微分方程式なら不定積分を$n$回繰り返せば解ける」と言えて、結果は$n$個の積分変数を含む。上の具体例を見ると、確かに一階微分方程式の解は1個の、二階微分方程式の解は2個の積分定数を含んでいる。
来々週がテストですが、テストではA41枚(裏使ってよし)の「自作カンニングペーパー」のみ、持ち込みを認めます。「自作」は友人との合作を含めます(コピーはダメ)。復習して勉強しつつ、まとめを作成して持ってきてください。