線形微分方程式
前回で、線形微分方程式の性質、特に重ね合わせの原理について考えた。
線形斉次微分方程式の重ね合わせ
微分演算子を${\cal D}$と書くことにすると、線形斉次方程式${\cal D}y=0$の解を$y_1\kakko{\xcol{x}}$と$y_2\kakko{\xcol{x}}$と二つ見つけたとすれば、 \begin{equation} \small\begin{array}{rlll} & {\cal D}y_1\kakko{\xcol{x}} &=0\\ & {\cal D}y_2\kakko{\xcol{x}} &=0\\ \hline & {\cal D}(y_1\kakko{\xcol{x}}+y_2\kakko{\xcol{x}})&=0 \end{array}\label{ConeCtwo} \end{equation} となり、解の和もまた解である。
非斉次の場合の重ねあわせ
非斉次の場合、つまり$\ycol{y}$の1次のみではなく$\ycol{y}$の0次の項がある線形微分方程式 \begin{equation} \left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +A_{n-1}\kakko{\xcol{x}}\left(\ddx\right)^{n-1} +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)\ycol{y} =C\kakko{\xcol{x}} \end{equation} の解を考えてみる。右辺においた、線形非斉次微分方程式の0次の項$C\kakko{\xcol{x}}$($\ycol{y}$を含んではいけないが、$\xcol{x}$の関数であってもよい)のことを「ソースターム(source term)」あるいは単に「源」または「ソース」と呼ぶ。話し言葉では「ソース」と呼ぶことが多い。このように呼ぶ理由は、このような方程式が「$C\kakko{\xcol{x}}$という量が$\ycol{y}\kakko{\xcol{x}}$を作り出す」という法則を表現することが多いからである。たとえば「ストーブがあるとまわりは温度が高い」「質量があるとまわりに重力場ができる」「電荷があるとまわりに電場ができる」などの場合「ストーブ」「質量」「電荷」が\ruby{源}{ソース}である(こういう現象も微分方程式で表現できるのだ)。この式の応用として面白いのは、以下の事実である。
線形非斉次微分方程式の重ね合わせ
「$C_1\kakko{\xcol{x}}$を源とする解」と「$C_2\kakko{\xcol{x}}$を源とする解」の和は「$C_1\kakko{\xcol{x}}+C_2\kakko{\xcol{x}}$を源とする解」。
これを数式で確認しておこう。
\begin{equation}
\begin{array}{rlll}
& \left(A_n\kakko{\xcol{x}}\left(\ddx\right)^n+\cdots+A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}}\right)y_1\kakko{\xcol{x}} &=C_1\kakko{\xcol{x}}\\
& \left(A_n\kakko{\xcol{x}}\left(\ddx\right)^n+\cdots+A_1\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}}
\right)y_2\kakko{\xcol{x}} &=C_2\kakko{\xcol{x}}\\
\hline
&
\left(A_n\kakko{\xcol{x}}\left(\ddx\right)^n+\cdots+A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}}\right)(y_1\kakko{\xcol{x}}+y_2\kakko{\xcol{x}})&=C_1\kakko{\xcol{x}}+C_2\kakko{\xcol{x}}\\
\end{array}
\end{equation}
となる「$C_1\kakko{\xcol{x}}$を源とする解」と「$C_2\kakko{\xcol{x}}$を源とする解」の線形結合の場合に拡張すれば、「$\alpha_1 C_1\kakko{\xcol{x}}+\alpha_2 C_2\kakko{\xcol{x}}$を源とする解」を作ることもできる。上の場合、$\alpha_1=\alpha_2=1$の場合である。$\alpha_1=1,\alpha_2=-1$にすれば「差」になる。}。次のようなことも言える。
非斉次方程式
\begin{equation}
\left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +A_{n-1}\kakko{\xcol{x}}\left(\ddx\right)^{n-1} +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)\ycol{y}=C\kakko{\xcol{x}}\label{hiseijirei}
\end{equation}
と、上の式で$C\kakko{\xcol{x}}=0$とした斉次方程式
\begin{equation}
\left( A_n\kakko{\xcol{x}}\left(\ddx\right)^n +A_{n-1}\kakko{\xcol{x}}\left(\ddx\right)^{n-1} +\cdots +A_{1}\kakko{\xcol{x}}\ddx +A_0\kakko{\xcol{x}} \right)\ycol{y} =0
\end{equation}
を考える。非斉次方程式の解として$y_1\kakko{\xcol{x}}$を1つ、斉次方程式の解として$y_0\kakko{\xcol{x}}$を1つ、それぞれ見つけたとする。${y_0}\kakko{\xcol{x}}+y_1\kakko{\xcol{x}}$もまた、非斉次方程式の解である。
これは上で考えたことの$C_2\kakko{\xcol{x}}=0$の場合にあたるから、証明は不要だろう。わざわざこんな(言わば、「あたりまえ」の)ことをここに書いたのは、この事実は応用範囲が広いからである。というのは、斉次方程式と非斉次方程式では当然斉次方程式の方が解きやすい。非斉次方程式の方の解は一つだけ求めておいて、斉次方程式の解を見つけられる限り見つけておけば、重ねあわせによって非斉次方程式の解をたくさん(見つけられる限り)見つけることができるようになる。 簡単な例をやってみよう。$\ddx \ycol{y}= \xcol{x}+\ycol{y}$という線形非斉次微分方程式を解きたい。これは「変数分離できる形」にはなってない。そこで試行錯誤で解を探す。たとえば$\ycol{y}=a\xcol{x}+b$が解になるだろうか、と考え代入してみると、
\begin{equation}
\begin{array}{rl}
\goverbrace{a}^{\tiny \ddx \ycol{y}}=& \xcol{x}+\goverbrace{a\xcol{x}+b}^{\ycol{y}}
\\
0=&(1+a)\xcol{x}+b-a
\end{array}
\end{equation}
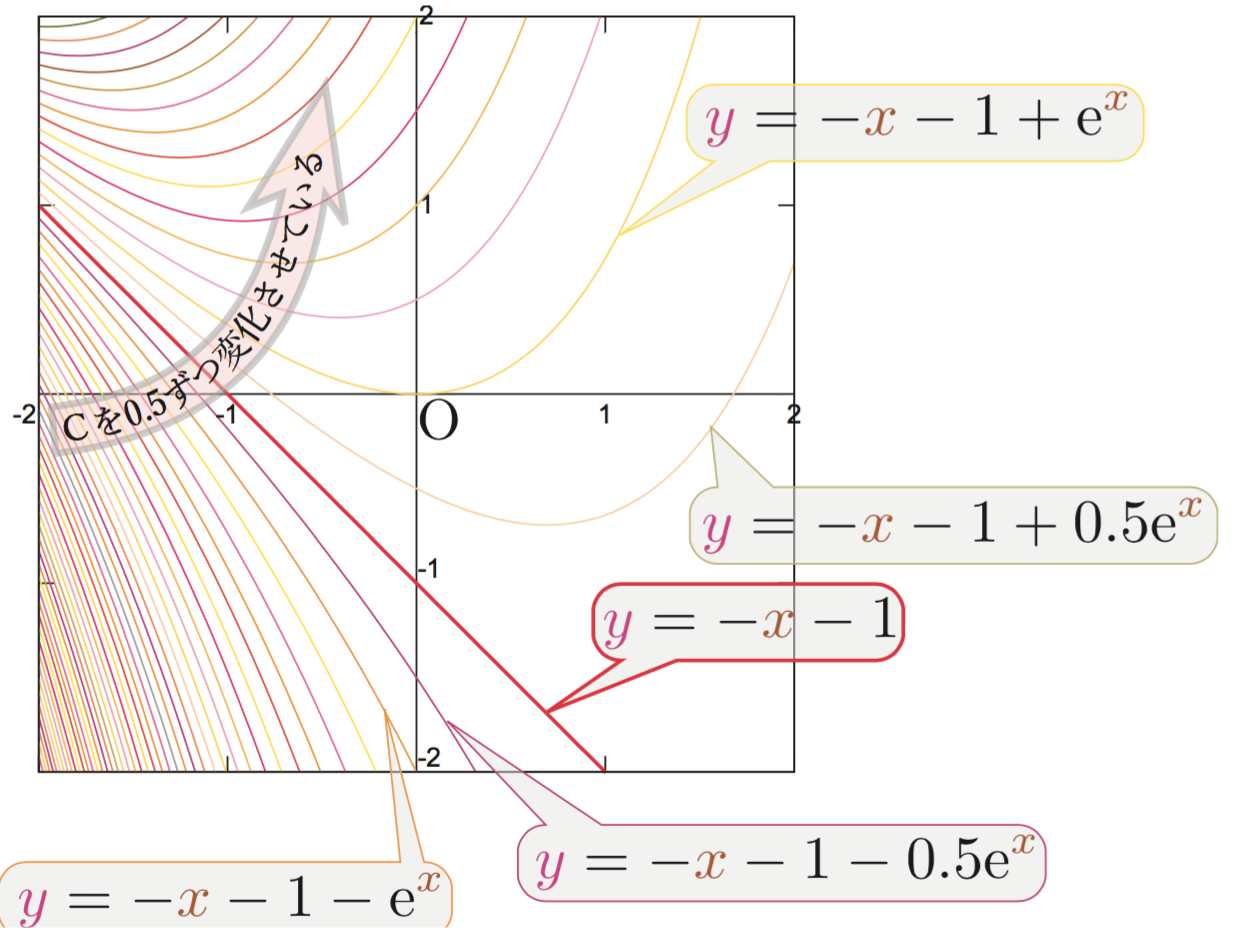
となるから、$a=-1,b=-1$にすれば解となる。 ゆえに、$\ycol{y}=-\xcol{x}-1$という解が見つかったわけだが、ここで「バンザイ、解が見つかった」と終わってはいけない。なぜなら関数$\ycol{y}=-\xcol{x}-1$は下のグラフであり、この線の上という(全$\xcol{x}$-$\ycol{y}$平面から見たらほんとに狭い)範囲の上での「解」を求めたに過ぎない。 この解は前に述べた特解であり、我々が求めたいのは全$\xcol{x}$-$\ycol{y}$平面を埋め尽くす、一般解である。 非斉次になっているのは$\xcol{x}$という項のせいだから、これを消して$\ddx \ycol{y}= \ycol{y}$という斉次方程式を作る。この方程式の解は、何度も出てきているお馴染みの$\ycol{y}=C \E^{\xcol{x}}$である。非斉次方程式の解は特解にこの斉次方程式の一般解を足せば作ることができる。 すなわち、一般解は
\begin{equation}
\ycol{y}=-\xcol{x}-1 + C\E^{\xcol{x}}\label{seijiippankai}
\end{equation}
となる。$C$を$0.5$ずつ変えた線を示すグラフが次の図である。 描かれている線と線の隙間にも線があり、解の曲線は全平面を埋め尽くし埋め尽くしていることを確認するには、任意の点の座標$(\xcol{x},\ycol{y})=(x_0,y_0)$を代入すると必ず一つ$C$が決まることを見る。この場合なら、$C=(y_0+x_0+1)\E^{-x_0}$である。微分方程式の形によっては解の曲線が通らない領域が存在することもあり得る(例えば、${\coldy\over \coldx}=\sqrt{1-\xcol{x}^2}$は$|\xcol{x}|>1$では解がない)。、どのような初期値$(x_0,y_0)$から出発しても、微分方程式に従うその後の変化がわかる。重ねあわせの原理のおかげで以上のような計算ができる。 以上で「線型非斉次微分方程式の一般解を求める」という問題は、
の二段階に分けられることがわかった。