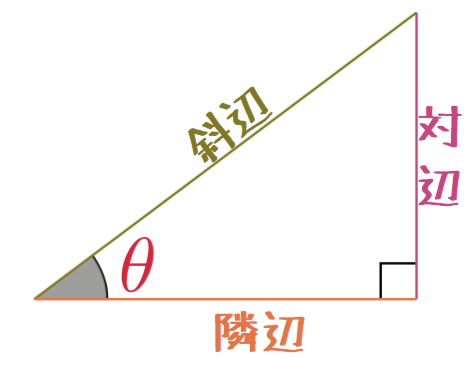
関数の平行移動
ここで関数の平行移動とはどういうものかを考えておこう。平面上のグラフを考えているから、基本的に平行移動は縦(${y}$方向)と横(${x}$方向)の二つがある(斜め方向は縦横の組み合わせだ)。
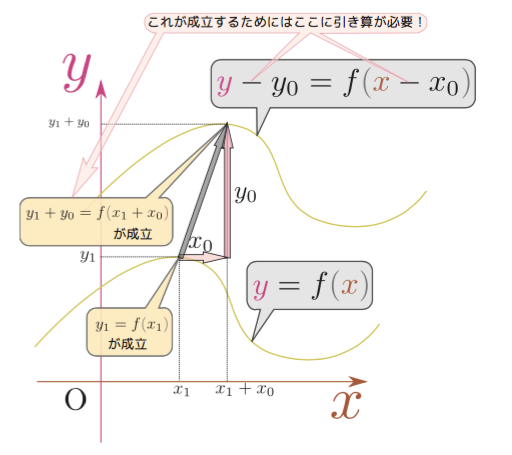
このグラフを${y}$方向に$y_0$だけ平行移動させるには、${y}\to {y}-y_0$と置き換えて、${y}-y_0=f({x})$という式に直せばよい。同様に${x}$方向に$x_0$だけ平行移動させるには、${x}\to{x}-x_0$と置き換えて${y}=f({x}-x_0)$という式に変える。両方を同時に行うと、 \begin{equation} {y}=f({x})~~{\rightarrow}~~{y}-y_0=f({x}-x_0) \end{equation} とすることで、${x}$方向に$x_0$、${y}$方向に$y_0$という平行移動が実現する。
一例として、移動前の関数が${x}=0$のとき${y}=1$を満たす関数だったとしよう(移動前の関数を${y}=f_前({x})$とすれば、$f_{前}(0)=1$)。${x}$方向に$x_0$平行移動させたとすると、移動後の関数は、${x}=x_0$のとき${y}=1$でなくてはいけない。移動後の関数を${y}=f_{後}({x})$(これは$f_{前}({x})$とは別の関数)とするならば、$f_後(x_0)=1$でなくてはいけない。$f_{前}(0)=1$と$f_後(x_0)=1$が両立するためには、$f_前({x}-x_0)=f_後({x})$になっていればよい(${x}=x_0$を代入すると$f_前(0)=f_後(x_0)$になる)。いわば、$x_0$を引くことによって関数の形を平行移動前に戻して、その後で${x}\to {y}$という対応関係を使っている、と思えばよい。
この平行移動によって、 \begin{equation} {y}= a{x}^2+b{x}+c ~~~\to~~~ {y}=a\left({x}-x_0\right)^2+b\left({x}-x_0\right)+c+y_0\label{shiftniji} \end{equation} と式が変わるが、結果を展開すれば \begin{equation} {y}= a{x}^2+\underbrace{(b-2ax_0)}_{新しいb}{x}+ \underbrace{a(x_0)^2-bx_0+c+y_0}_{新しいc} \end{equation} となる。つまり$x$方向の平行移動は1次の係数と0次の係数を変える。

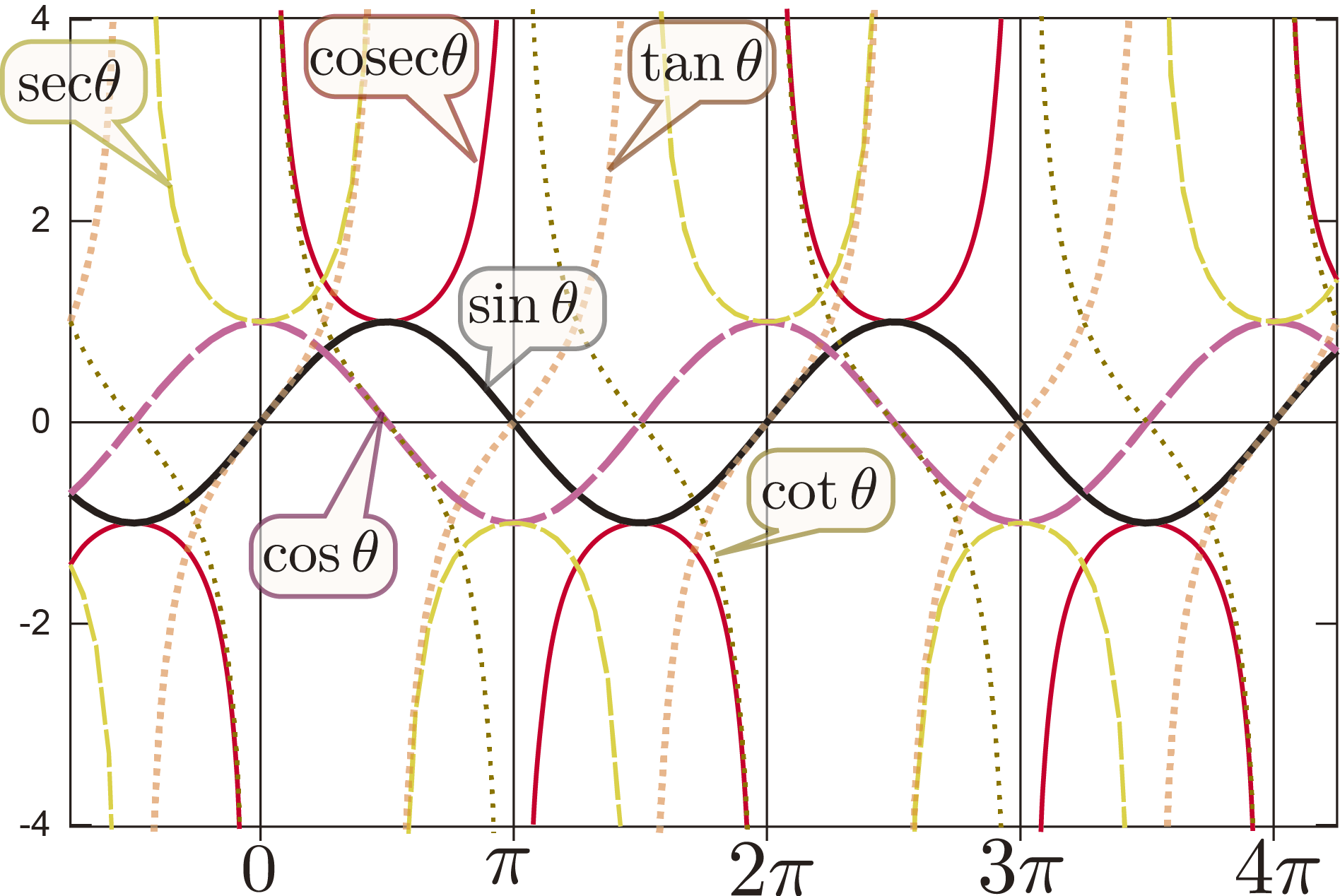
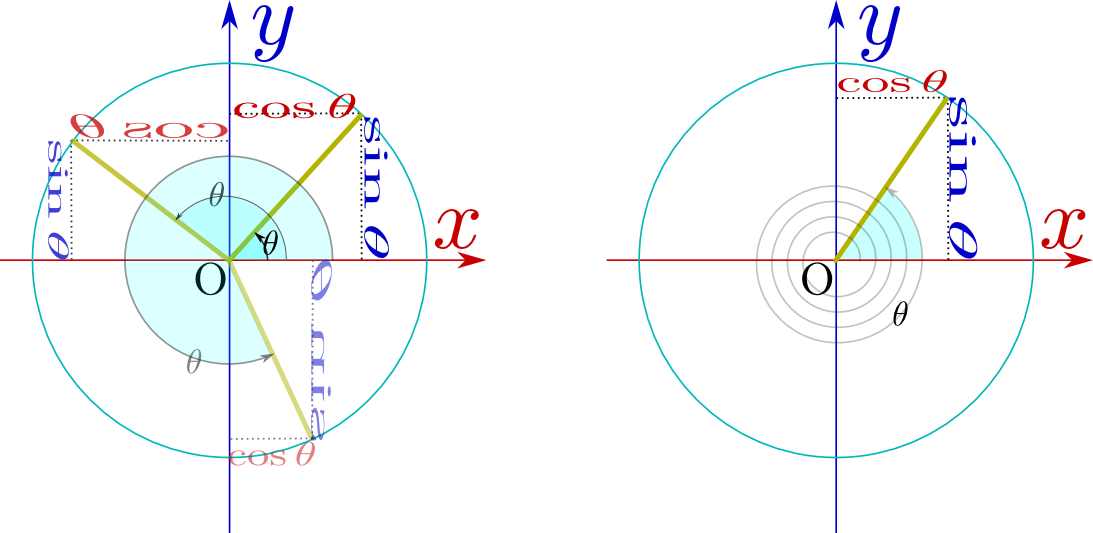
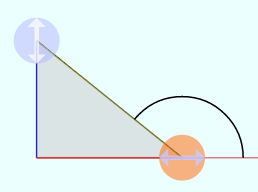 のようにθが直角より大きくなり「
のようにθが直角より大きくなり「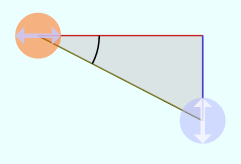 のようにθが負になり「
のようにθが負になり「 から
から に向かう方向が「上」「右」の時にsin,cosは正であり、「下」「左」の時にはsin,cosは負である。図ではそれを
に向かう方向が「上」「右」の時にsin,cosは正であり、「下」「左」の時にはsin,cosは負である。図ではそれを や
や が鏡文字になることで表現している。
が鏡文字になることで表現している。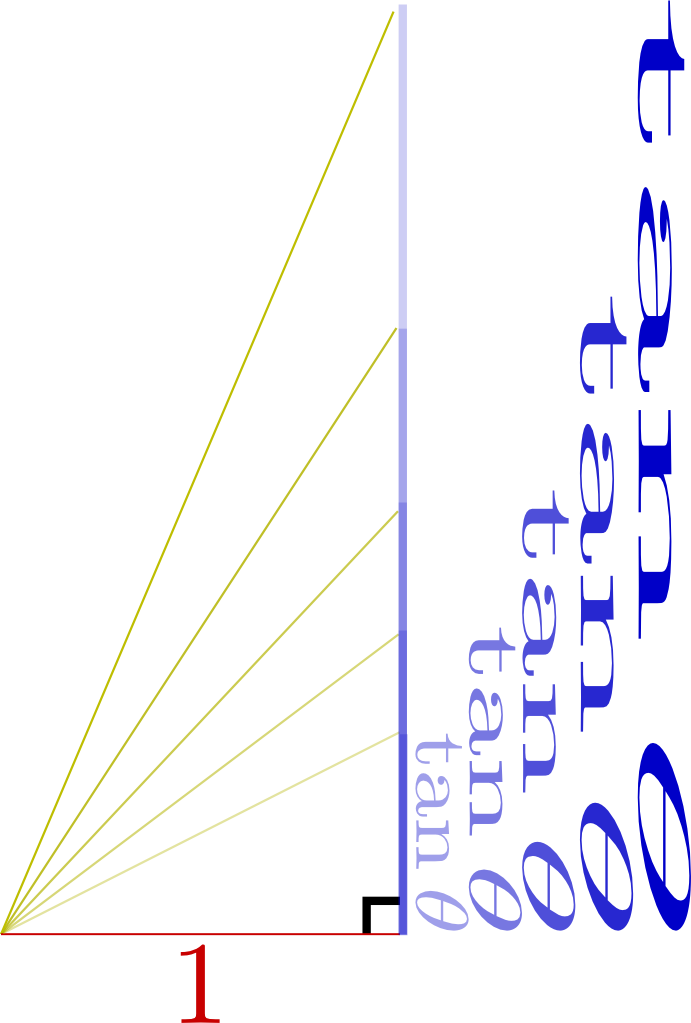

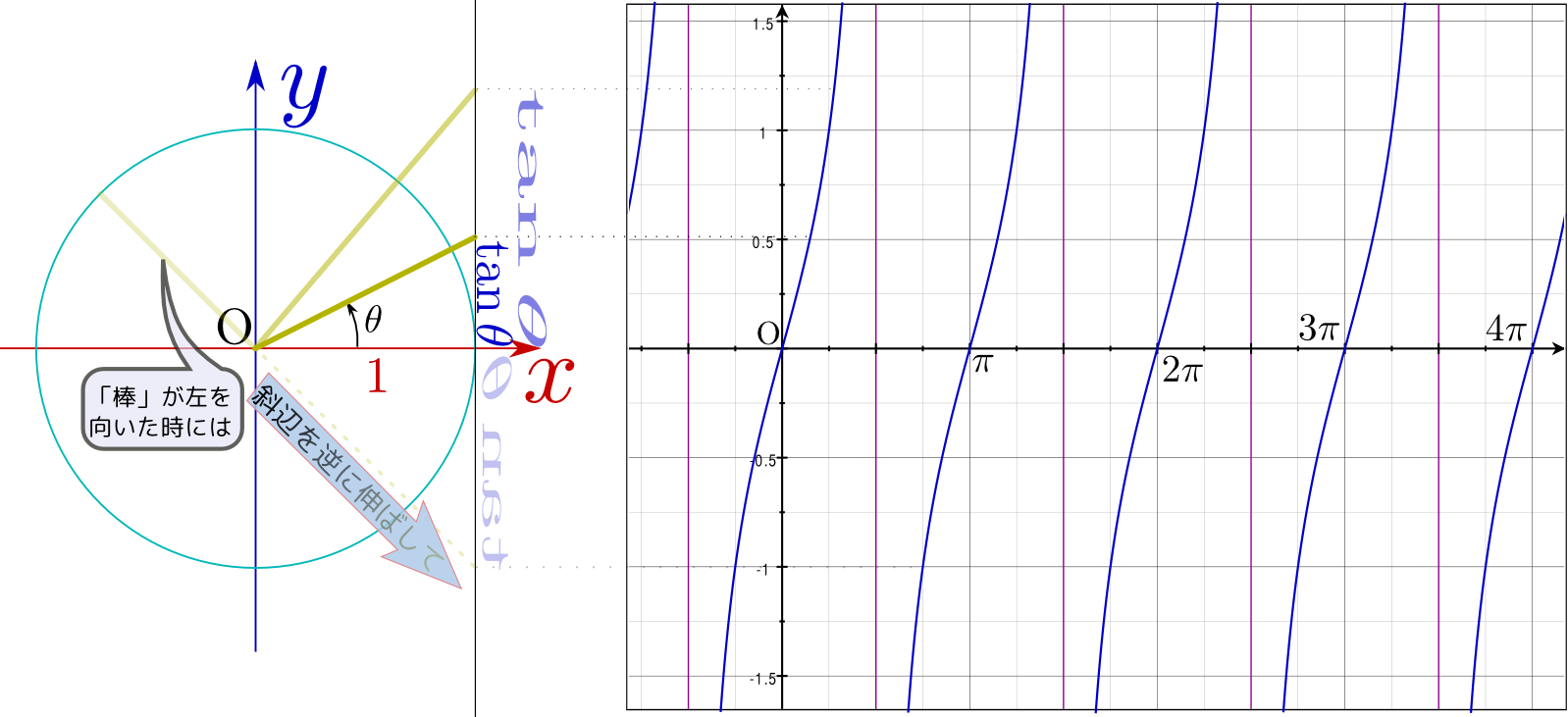
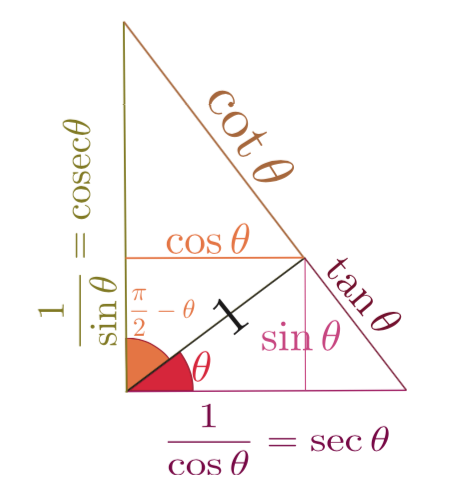
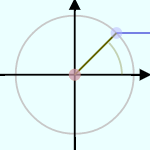 は半径1の円(単位円)を描いたもので、中心から円周の一点に向かっている棒
は半径1の円(単位円)を描いたもので、中心から円周の一点に向かっている棒 の角度に応じて、
の角度に応じて、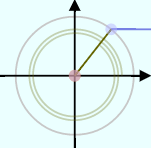 のように2πより大きい(何周も回る)角度にしたり、
のように2πより大きい(何周も回る)角度にしたり、 のように負の角度にしたりもできるので、いろいろ変えて状況を確認して欲しい。
のように負の角度にしたりもできるので、いろいろ変えて状況を確認して欲しい。
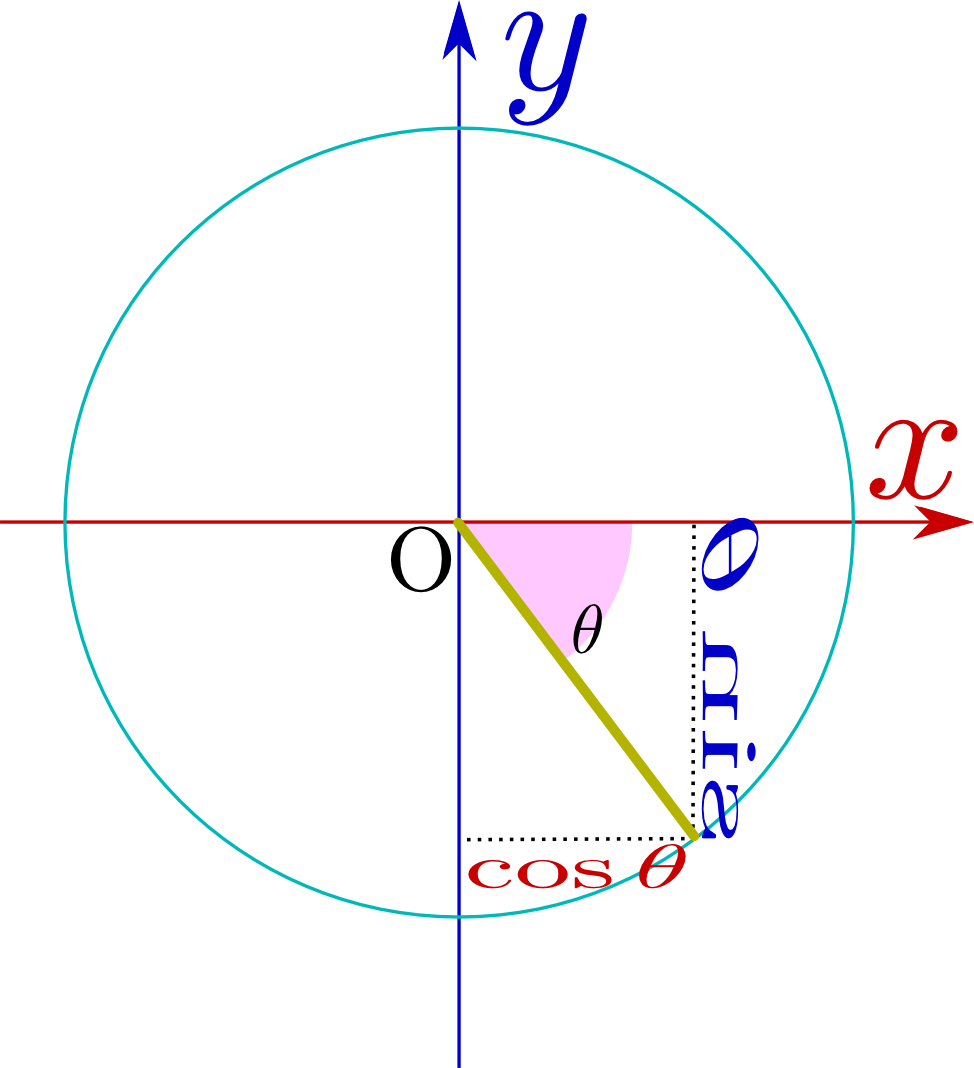
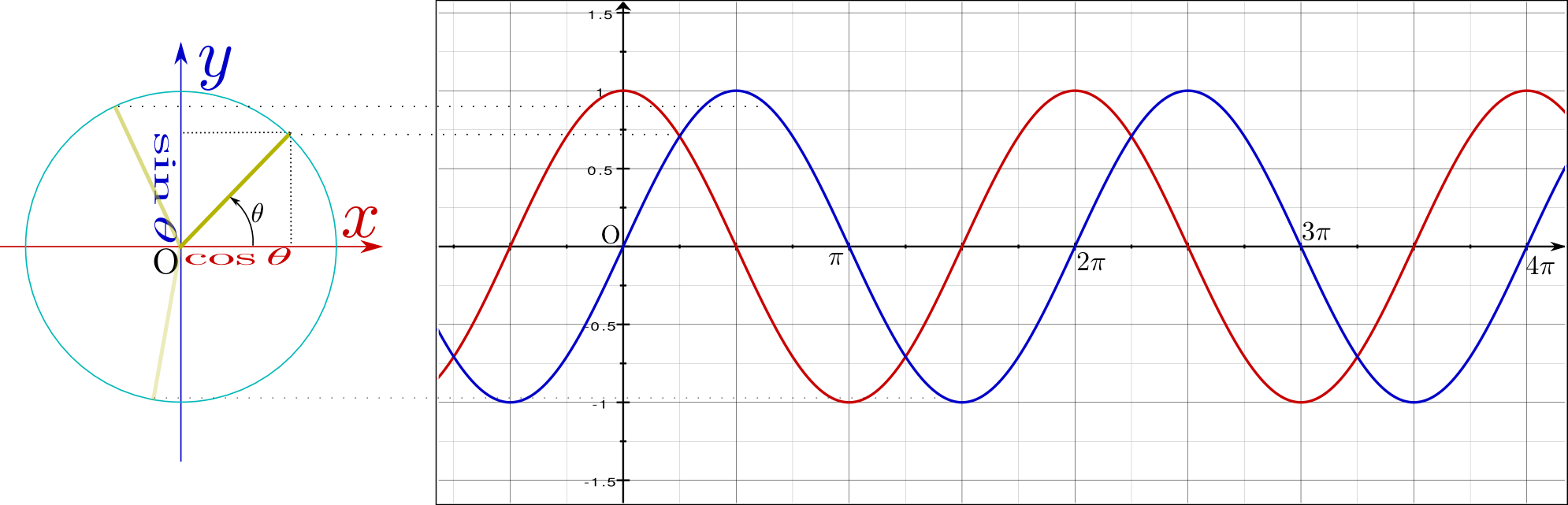
 の部分の薄い色になっている
の部分の薄い色になっている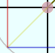 の方が、θよりπラジアン(180度)大きい角度の場合の「長さ1の棒」になっている。sin,cosがπ足されることでどう変化するかを、図から読み取っていけば、公式が作られる(この公式は式として覚えようとしなくても、意味を考えればすぐにわかる)。
の方が、θよりπラジアン(180度)大きい角度の場合の「長さ1の棒」になっている。sin,cosがπ足されることでどう変化するかを、図から読み取っていけば、公式が作られる(この公式は式として覚えようとしなくても、意味を考えればすぐにわかる)。