弱肉強食の微分方程式
兎と狐の増減
ある森の中で草食動物(兎)の数$\rcol{X}$と肉食動物(狐)の数$\thetacol{Y}$がどう増減するかを考える(簡単のため、この森にはこの2種類の動物しかいないものとする)。
餌が豊富にあり、かつ狐がいないと考えた場合、兎は今いる量に比例して増えると同時に寿命が来て死ぬ分減る(減る量も今いる量に比例する)。この二つの効果のみを考えるならば、 \begin{equation} \opcol{\diff\rcol{X}\over \kidt}= A\rcol{X}\label{lwonezero} \end{equation} という微分方程式で兎の数$\rcol{X}$の変化が記述できそうである。ただし$A$は比例定数で兎は自然には増えるということを反映して、正の定数となる。
ところが兎が減る原因はもう一つある。狐は兎を食べるので、兎は狐と出会うと死ぬと考えよう。森の中に$\rcol{X}$匹の兎と$\thetacol{Y}$匹の狐がそれぞれ動きまわっている状況を考えると、両者が出会う確率は$\rcol{X}$と$\thetacol{Y}$の積に比例するだろう。そして出会った後でやはりある確率で「狐が兎を食べる」というイベントが発生し、兎が減る。このように考えると、兎の減少量として$\rcol{X}\thetacol{Y}$という積に比例する部分が出てくる。よって、兎の数は \begin{equation} \opcol{\diff\rcol{X}\over \kidt}= A\rcol{X} -B\rcol{X}\thetacol{Y}\label{lwone} \end{equation} という式で増減するとする($B$は$A$とは別の比例定数)。
一方狐は、兎を食べないと生きていけないのだから、その増加はどれだけ兎を食べられるかによって決まり、それは$\rcol{X}\thetacol{Y}$に比例するのだったから、狐は$\rcol{X}\thetacol{Y}$に比例して増える。兎がいなかったら狐は「繁殖しつつ寿命が来て死ぬ」という現象の結果として現在いる量に比例して減っていくだろう。それを$-C\thetacol{Y}$という形($C$は正の定数、ほっておくと増える兎とは符号が逆になる)で式の右辺に入れて、 \begin{equation} \opcol{\diff\thetacol{Y}\over \kidt}= -C \thetacol{Y} + D \rcol{X}\thetacol{Y}\label{lwtwo} \end{equation} という微分方程式に従う($C,D$は$A,B$とは別の比例定数である)。これらの方程式はこの式を出した二人の数学者の名前を取って「ロトカ・ヴォルテラの方程式」と呼ばれる。
時間変化を考えるには、$\opcol{\diff \rcol{X}\over \kidt},\opcol{\diff\thetacol{Y}\over \kidt}$に関する二つの微分方程式を連立させて解けばよい。
いきなり解けと言われても、どうしていいのか悩んでしまうかもしれない(この式は非線形だし)。そこでまず、「$\opcol{\diff \rcol{X}\over \kidt}=\opcol{\diff\thetacol{Y}\over \kidt}=0$となるのはどんなときか?」から考える。$\opcol{\diff \rcol{X}\over \kidt}=\opcol{\diff\thetacol{Y}\over \kidt}=0$となる点を「固定点」と呼ぶ。
固定点を求める方程式は上の微分方程式の右辺が$0$になる、という式で、因数分解すれば \begin{eqnarray} \rcol{X}(A-B\thetacol{Y})&=&0\\ \thetacol{Y}(-C+D\rcol{X})&=&0 \end{eqnarray} である。$\rcol{X}=\thetacol{Y}=0$もこの方程式の解だが、「兎も狐もいない」という「つまらない解」最初から兎も狐もいないのだから、未来永劫いないままである。なので無視する。
$\rcol{X}={C\over D},\thetacol{Y}={A\over B}$が意味のある固定点である。
固定点からずれた時の$\opcol{\diff\rcol{X}\over\kidt},\opcol{\diff \thetacol{Y}\over\kidt}$の様子をグラフに表示すると次のグラフのようになる。
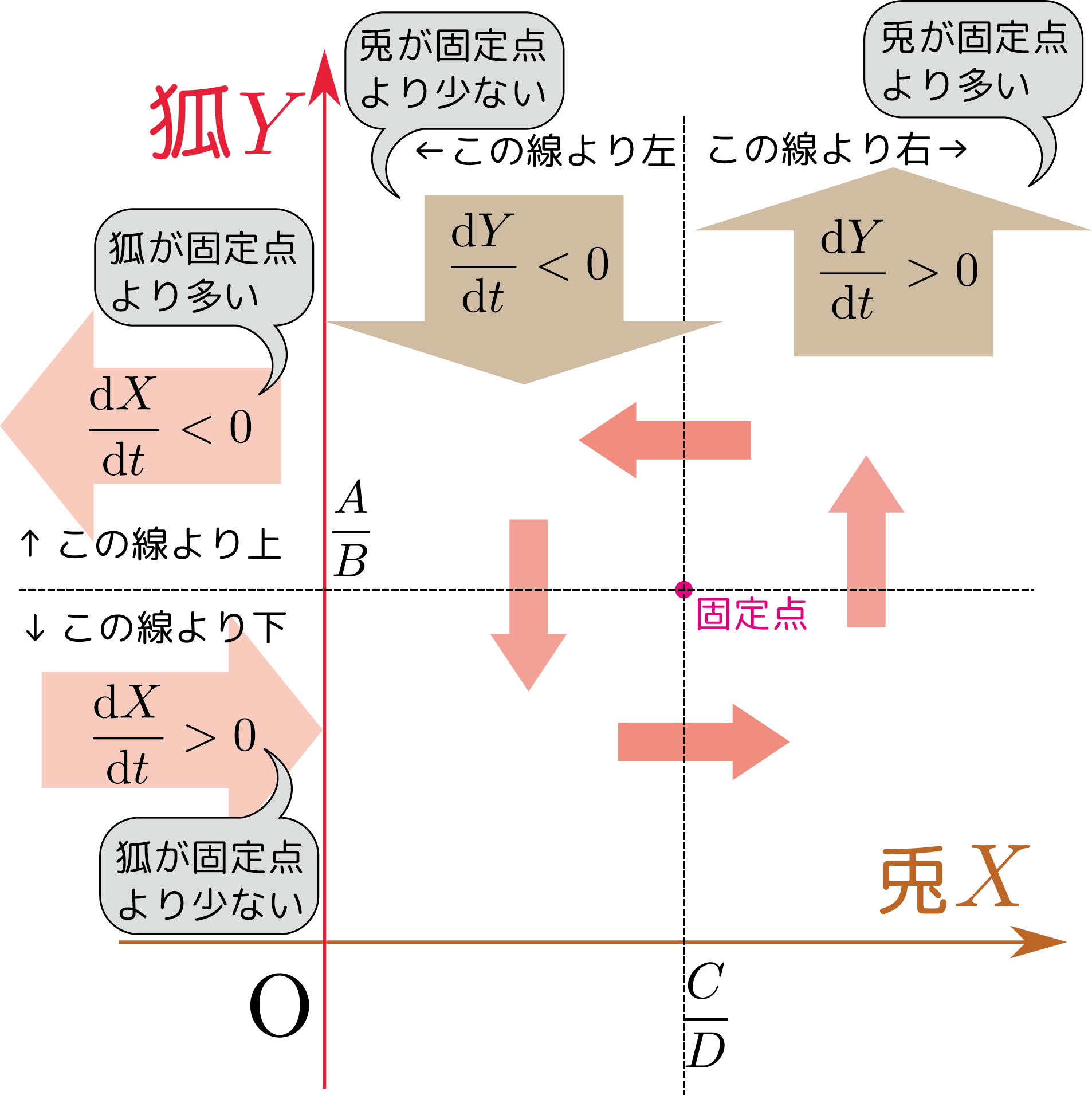
これから$\rcol{X}$-$\thetacol{Y}$平面内で反時計周りにぐるぐる回るような時間発展を行うということが予想される。
固定点からのずれを$\xcol{x},\ycol{y}$とする。つまり、 \begin{equation} \rcol{X}= {C\over D}+\xcol{x},~~\thetacol{Y}={A\over B}+\ycol{y} \end{equation} とする。こうして$\xcol{x},\ycol{y}$の微分方程式を作ると、 \begin{equation} {\coldx\over \coldt}= -B \left({C\over D}+\xcol{x}\right) \ycol{y},~~~ {\coldy \over \coldt}= D\left({A\over B}+\ycol{y}\right)\xcol{x} \end{equation} となる。ここで$\xcol{x},\ycol{y}$は${C\over D},{A\over B}$に比べて小さいと考えて、括弧内の$\xcol{x},\ycol{y}$は無視して、 \begin{equation} {\coldx\over \coldt}= -{BC\over D} \ycol{y},~~~ {\coldy \over \coldt}= {AD\over B} \xcol{x} \end{equation} と近似する。第一式を微分して \begin{equation} {\coldtwox\over \coldt^2}= -{BC\over D} {\coldy\over \coldt} \end{equation} にしてから第二式を代入すると \begin{equation} {\coldtwox\over \coldt^2}= -{BC\over D}\times{AD\over B}\xcol{x}=-{AC}\xcol{x} \end{equation} という、係数は違うが単振動と同じ式が出てくる。解はすでに知っていて、 \begin{equation} x\kakko{\tcol{t}}=x_0 \cos\kakko{\sqrt{AC}\tcol{t}+\alpha} \end{equation} と書ける。
授業ではこの↑解が質問してもすぐに出てこなくてびっくりした。これぐらいはささっと出てくるようでないと勉強が足りない。これを覚えるべきということではなく、普通に勉強していれば何度でもこの式が出てきて覚えてしまっているはず、ということ。
$\cos$の中の$\tcol{t}$の前に$\sqrt{AC}$がついているのは、この微分方程式が「二階微分すると元の$-AC$倍になる」という式だからである。$x_0,\alpha$は微分方程式からは決まらないパラメータである(二階微分方程式だからこれでちょうどよい)。
${\coldx\over \coldt}=-{BC\over D} \ycol{y}$なので、$\sqrt{AC}=\omega$として \begin{equation} \begin{array}{rl} -\omega x_0 \sin\kakko{\omega \tcol{t}+\alpha}= &-{BC\over D} y\kakko{\tcol{t}} \\ {D\over BC}\times\omega x_0 \sin\kakko{\omega \tcol{t}+\alpha}= &y\kakko{\tcol{t}} \end{array} \end{equation} で$\ycol{y}$も求まる。
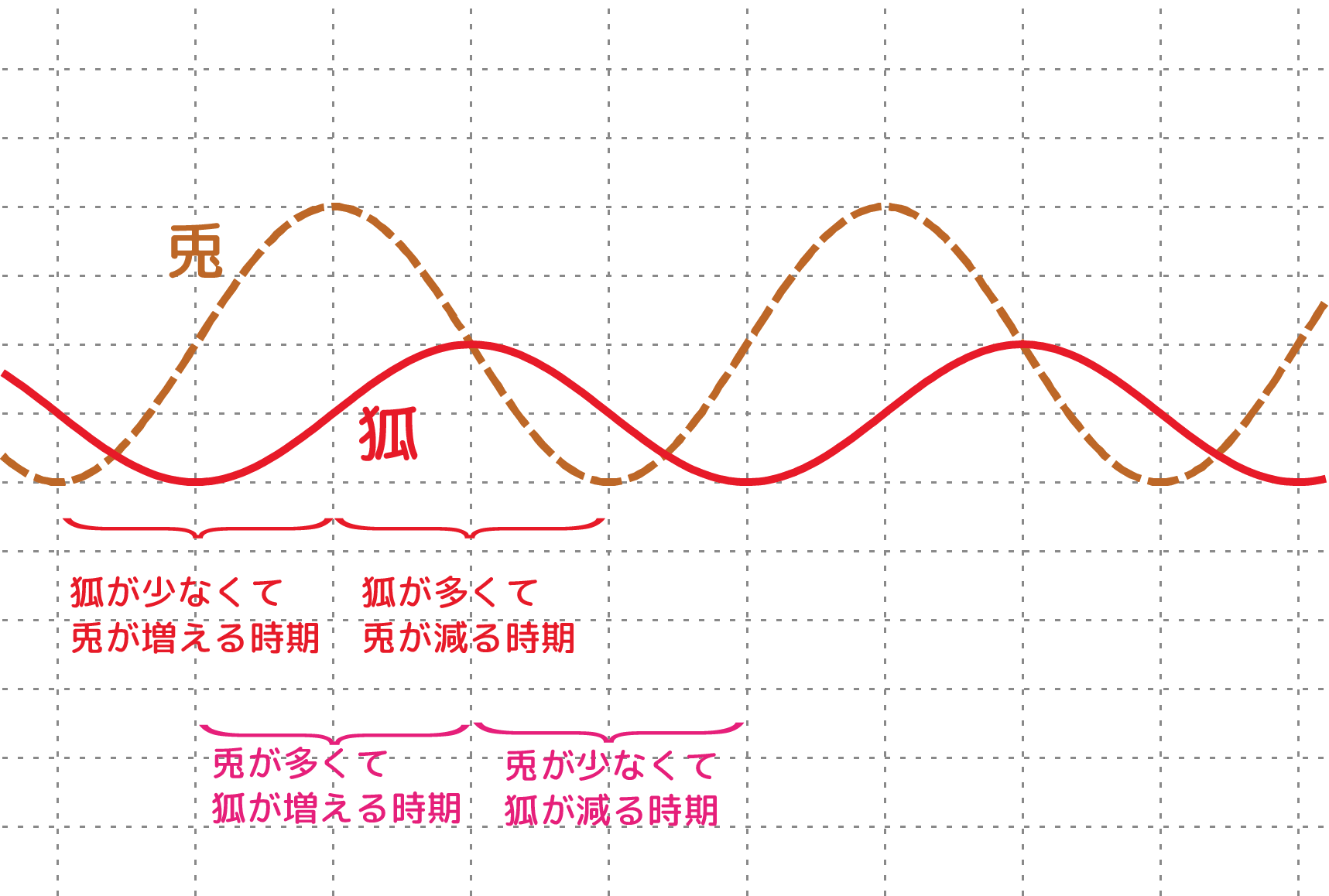
$\rcol{X},\thetacol{Y}$の時間変化を表すのが左のグラフである。$\xcol{x},\ycol{y}$と$\rcol{X},\thetacol{Y}$は定数を足しただけの違いなので、$\rcol{X}$(兎)の変化は$\cos$で、$\thetacol{Y}$(狐)の変化は$\sin$で表されていると思えばよい。
グラフに示したように、狐のグラフが「山」である間は兎のグラフは右下がり、狐のグラフが「谷」である間は兎のグラフが右上がりとなる。もちろんこれは「狐が多くて兎が食われる時期は兎が減り、狐が少なくなると兎が増える」を示している。逆に「兎が多いと狐が増える(およびこの逆)」もわかる。グラフを見ながらそれを確認してみよう。
ここで、時間変化が周期的になること、つまりある程度の時間がたつと(正確に言えば$\tcol{t}$が${2\pi\over \sqrt{AC}}$だけ増加すると)$\rcol{X}$と$\thetacol{Y}$は元の値に戻るということに注意しよう。
ここまでで求めたのは近似解なので、$\rcol{X}$-$\thetacol{Y}$平面に描かれる図形は単純な楕円であるが、実際に微分方程式を解いてみると少々複雑な図形を描く(次のグラフではコンピュータで数値的に計算させた)。
動くグラフはにある。
グラフでは$A=B=C=D=1$にして、$\rcol{X},\thetacol{Y}$の初期値を変えてグラフにしている。この場合は$(\rcol{X},\thetacol{Y})=(1,1)$が固定点であり、その周りをめぐる軌跡を描く。固定点からの外れが小さい領域では軌跡は円に近い(円なのは今の場合は${D\over BC}=1$だから)。