偏微分の定義
偏微分の定義と記号
ここまでで説明したように、2変数関数では微分が(最低)2種類ある。
- $\ycol{y}$を一定にして$\xcol{x}$を変化させたときの変化の割合
- $\xcol{x}$を一定にして$\ycol{y}$を変化させたときの変化の割合
で、それぞれ「$\xcol{x}$方向の微分」と「$\ycol{y}$方向の微分」となる。
この新しい形式の微分に名前と定義と、そして新しい記号を与えよう新しい記号が出て来ると「ああ、難しい話が始まった」とその記号を使うことに心理的拒否反応を示す人が時々いるのだが、上で書いたような「ちょっと違う微分」はこれまでも無意識に使っていたはずである。以下は、それに新しい名前をつけようというだけのことであるから、難しく考え過ぎないように。。
上で述べたような「実際は変数であるものを定数であるかのごとく扱って微分する」微分を「偏微分(partial differential)」と呼ぶ。名前の通り「肉と野菜を出されたのに、偏食して、肉しか食べない」という時の「偏」である。partialは「一部だけ」を意味している。「偏りのある微分」で、変数が二つ(ときには、三つ以上)あるのに、その変数のうち一個だけに着目して微分を行う。これまでの微分を区別のために「常微分(ordinary differential)」と呼ぶordinaryは「普通」なので「常」と訳すのは変に思う人もいるだろうが、この訳が定着している。ことにする。常微分の導関数または微係数は $$ \ddx f\kakko{\xcol{x}}=\lim_{\xcol{\Delta x}\to0}{f\kakko{\xcol{x}+\xcol{\Delta x}}-f\kakko{\xcol{x}}\over \xcol{\Delta x}} $$ と定義されていた。
偏微分は常微分とは違う記号を使うことにして、「導関数」または「微係数」にあたるものを「偏導関数(partial derivative)」または「偏微係数(偏微分係数)」と呼び、
偏導関数の定義
\begin{equation} \PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}= \lim_{\xcol{\Delta x}\to0}{ f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}}-f\kakko{\xcol{x},\ycol{y}} \over \xcol{\Delta x} } \end{equation}
と書くことにしよう。もう一つの変数$\ycol{y}$がついている(しかし定数として扱っている)以外は常微分と同じ計算である。
偏微分は$\diff$ではなく$\partial$という記号を使い、かつ「(本当は変数なんだけど)定数として扱っている文字」を$\opcol{\left(~~\right)}_{\!\ycol{y}}$のように括弧の後に下付き添字としてつけて表現する(誤解が起こらないだろうと思われる時は省略され関数の引数が$\kakko{\xcol{x},\ycol{y}}$だから、$\xcol{x}$で微分するなら$\ycol{y}$が一定なのは当然でしょ、という考え方をする。、単に$\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}$と書く場合も多いさらに$\PD{f}{\xcol{x}}$のように関数の引数も省略されている場合もあるが、その場合は文脈を読んで判断することになる(文脈からは判断しにくい場合は省略すべきではない)。)。$\PD{f\kakko{\xcol{x},\ycol{y}}}{{\xcol{x}}}\biggr|_{\ycol{y}}$のように、偏微分記号の後に縦線を引いてその右下に書くという書き方もある。
記号$\partial$はいろんな読み方がある。「丸いd」という意味で「ラウンドディー」と読む場合、それを省略して単に「ラウンド」と読む場合、偏微分(partial differential)から「パーシャル」と読む場合、derivativeの方から「デル」と読む場合がある。微分${\coldy\over \coldx}$を「でぃーわいでぃーえっくす」と読んだのと同様に、$\PD{f}{{\xcol{x}}}$は「でるえふでるえっくす」(あるいは「らうんどえふらうんどえっくす」)のように上から順に読む。
もちろん、立場を入れ替えた$\xcol{x}$を一定として$\ycol{y}$で偏微分は \begin{equation} \PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} =\lim_{\ycol{\Delta y}\to0}{ f\kakko{\xcol{x},\ycol{y}+\ycol{\Delta y}}-f\kakko{\xcol{x},\ycol{y}} \over \ycol{\Delta y} }\label{delfdely} \end{equation} である。どちらも、一方で微分する時はもう一方をあたかも定数であるかのように扱っている。ここまでの話として、常微分が偏微分に変わったことで特に難しいところはないはずだ。
計算も常微分と同様に行うことができる。たとえば\文中式{$\ycol{y}=\xcol{x}^2$}に含まれる変数$\xcol{x},\ycol{y}$を微小変化させた式は\文中式{$\ycol{y}+\coldy=(\xcol{x}+\coldx)^2=\xcol{x}^2+2\xcol{x}\coldx$}であり、この式の$\coldx,\coldy$の1次の項の係数を見ることで\文中式{$\coldy=2\xcol{x}\coldx$}または\文中式{${\coldy\over \coldx}=2\xcol{x}$}のようにすることで導関数${\coldy\over \coldx}$を求めることができた。
$f\kakko{\xcol{x},\ycol{y}}= \xcol{x}^2\ycol{y}$の微分を考えるには \begin{equation} \left(\xcol{x}+\coldx\right)^2\left(\ycol{y}+\coldy\right)=\xcol{x}^2\ycol{y}+2\xcol{x}\ycol{y}\coldx +\xcol{x}^2\coldy \end{equation} のように計算することで、 \begin{equation} \begin{array}{lcll} &\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{{\xcol{x}}}{\ycol{y}}= 2\xcol{x}\ycol{y},&\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}= \xcol{x}^2\\[6mm] \end{array} \end{equation} となる。同様に$f\kakko{\xcol{x},\ycol{y}}= \sin (\xcol{x}+\ycol{y}^2)$の場合を考えると \begin{equation} \begin{array}{lcll} &\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}= \cos\kakko{\xcol{x}+\ycol{y}^2},&\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}=2\ycol{y}\cos\kakko{\xcol{x}+\ycol{y}^2}\\ \end{array} \end{equation} である。
前にやった円柱の体積の例では、 \begin{equation} \mathrm dV\kakko{\rcol{r},\xcol{h}} = \overbrace{\pi \rcol{r}^2}^{\PDC{V}{\xcol{h}}{\rcol{r}}}\xcol{\mathrm dh} + \overbrace{2\pi\rcol{r}\xcol{h}}^{\PDC{V}{\rcol{r}}{\xcol{h}}}\rcol{\mathrm dr} \end{equation} となっている。この例の場合、偏微分係数である$\PDC{V}{\xcol{h}}{\rcol{r}},\PDC{V}{\rcol{r}}{\xcol{h}}$は底面積と側面積という意味のある量になるこのようにある物理量の偏微分係数がまた別の物理量になる、ということはよくある。一つの物理量を偏微分することでいろんな物理量がわかるようになっている。。
ここで標語を書いておこう。
偏微分では「どの方向の変化に対する変化量なのか」が常に大事である。
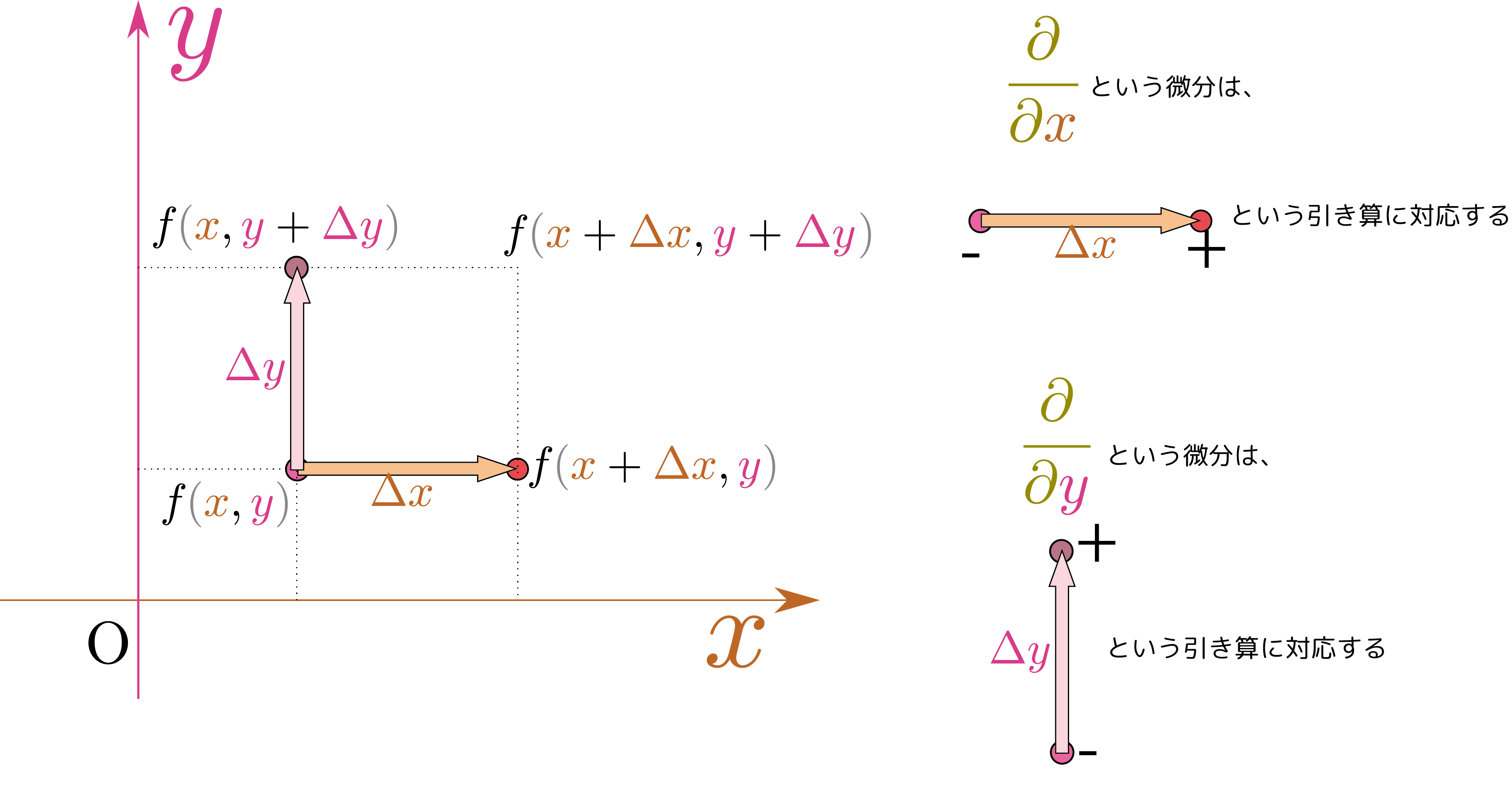
上の図に、二つの微分の意味を図解した。矢印の先(+と書いたところ)から矢印の根元(ーと書いたところ)を引く、というのが(たとえば$f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}}-f\kakko{\xcol{x},\ycol{y}}$)が偏微分という計算の本質になるこの後$\xcol{\Delta x}$で割って$\xcol{\Delta x}\to0$の極限を取って、という手続きが続くが、本質は「矢印の先と元の引き算」なのである。
微分の表現として、$f\kakko{\xcol{x}+\coldx}=f\kakko{\xcol{x}}+f'\kakko{\xcol{x}}\coldx$もしくは、$\mathrm df=f'\kakko{\xcol{x}}\coldx$という書き方具体例で示せば、$\cos\kakko{\xcol{x}+\coldx}=\cos \xcol{x}-\sin\xcol{x}\coldx$もしくは$\diff (\cos\xcol{x})=-\sin\xcol{x}\coldx$など。があったが、偏微分における同様の書き方が \begin{equation} f\kakko{\xcol{x}+\coldx,\ycol{y}+\coldy} =f\kakko{\xcol{x},\ycol{y}}+ \PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}\coldx +\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy\\[6mm] \end{equation} もしくは \begin{equation} \mathrm df\kakko{\xcol{x},\ycol{y}}=\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}\coldx +\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy \label{zenbibun} \end{equation} である。これを示すには、変化量の式を \begin{equation} f\kakko{\xcol{x}+\coldx,\ycol{y}+\coldy}-f\kakko{\xcol{x},\ycol{y}} = f\kakko{\xcol{x}+\coldx,\ycol{y}+\coldy}\underbrace{ -f\kakko{\xcol{x}+\coldx,\ycol{y}} +f\kakko{\xcol{x}+\coldx,\ycol{y}}}_{0}-f\kakko{\xcol{x},\ycol{y}} \end{equation} のように間に0になる量を挟んでから、前の2項が \begin{equation} f\kakko{\xcol{x}+\coldx,\ycol{y}+\coldy}-f\kakko{\xcol{x}+\coldx,\ycol{y}} =\PDC{{f\kakko{\xcol{x}+\coldx,\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy \end{equation} に$\coldx,\coldy$の1次の項までを考えているので、$\PDC{{f\kakko{\xcol{x}+\coldx,\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy=\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\ycol{y}}{\xcol{x}}\coldy$である。、後の2項が \begin{equation} f\kakko{\xcol{x}+\coldx,\ycol{y}}-f\kakko{\xcol{x},\ycol{y}}=\PDC{{f\kakko{\xcol{x},\ycol{y}}}}{\xcol{x}}{\ycol{y}}\coldx \end{equation} になると考えればよい。この式は上と同じ意味を持つ式である。上の例に則して書けば、 \begin{equation} \begin{array}{rll} \diff \overbrace{(\xcol{x}^2\ycol{y})}^{f\kakko{\xcol{x},\ycol{y}}}=&\overbrace{2\xcol{x}\ycol{y}}^{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}\coldx&+\overbrace{\xcol{x}^2}^{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}\coldy\\[2mm] \diff\goverbrace{ (\sin(\xcol{x}+\ycol{y}^2))}^{f\kakko{\xcol{x},\ycol{y}}}=&\goverbrace{\cos\kakko{\xcol{x}+\ycol{y}^2}}^{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}\coldx &+ \goverbrace{2\ycol{y}\cos\kakko{\xcol{x}+\ycol{y}^2}}^{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}\coldy \end{array} \end{equation} となる。新しい記号を使ってはいるが、この計算は別に目新しいものではない。偏微分は単に「本当は定数である文字を定数とみなして微分する」というだけで計算テクニックとして難しい点は無い(偏微分ならではの注意点は現段階ではまだ出てきていない。後で登場する)。
二階偏微分と多変数関数の極大極小
偏微分も常微分同様、二階微分がある。その記号も \begin{equation} \PDIC{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}{\xcol{x}}{\ycol{y}} =\PPDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} ,~~ \PDIC{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}{\ycol{y}}{\xcol{x}} =\PPDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \end{equation} のように常微分の場合に似た書き方にする(三階以上も同様である)。これら二つの偏微分が(それぞれ$\xcol{x}$方向と$\ycol{y}$方向の)曲がり具合を表現しているのは、1変数の場合と同様である。
偏微分の二階微分には、 \begin{equation} \PDIC{\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}{\xcol{x}}{\ycol{y}}=\PPDD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \end{equation} のように「最初に$\ycol{y}$で微分、次に$\xcol{x}$で微分」もある(上の式の右辺は固定する変数を省略する書き方を使った$\PPDD{f}{\xcol{x}}{\ycol{y}}$は$\PD{}{\xcol{x}}\left(\PD{f}{\ycol{y}}\right)$の省略形と考えよ。)。分母の書き方が常微分と決定的に違うところなので注意しよう。
ここで、$\PPDD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$と$\PPDD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}$は違うのか?---という疑問を持った人もいるだろう。微分可能な関数に対してはこの二つは等しい。詳しくは次回説明するので、しばらくの間は「そういうものだ」と思って進めよう。
偏微分の記号には省略形がいくらかある。たとえば「変数が$\xcol{x},\ycol{y}$の二つであることはわかっているから、$\xcol{x}$で偏微分するなら$\ycol{y}$が一定なのは書かなくてもわかるだろう」と判断できる場合は、$)_{\!\!\ycol{y}}$を省略して、$\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}$と書く場合がある。また、$\PDC{?}{\xcol{x}}{\ycol{y}}$を$\opcol{D_x}?$のように短縮形で書く場合もあり、 \begin{equation} \opcol{D_x} f=\PD{f}{\xcol{x}},~~\opcol{D_y} f=\PD{f}{\ycol{y}},~~\opcol{D_x}\opcol{D_x} f=\PPD{f}{\xcol{x}},~~\opcol{D_x}\opcol{D_y} f=\PD{}{\xcol{x}}\left(\PD{f}{\ycol{y}}\right)=\opcol{\partial^2\kuro{f}\over \partial x\partial y},\cdots \end{equation} のように表現する。あるいは、微分記号も書かずに、 \begin{equation} f_x=\PD{f}{\xcol{x}},~~f_y=\PD{f}{\ycol{y}},~~f_{xx}=\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}^2},~~f_{xy}=\PD{}{\xcol{x}}\left(\PD{f}{\ycol{y}}\right)=\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}\partial \ycol{y}},\cdots \end{equation} のように微分を下付き添字をつけることで表現する場合もある。
関数$f\kakko{\xcol{x},\ycol{y}}$の第1の引数に関する偏微分は$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$だが、同じ関数を$f\kakko{\tcol{t},\ycol{y}}$のように変数を変えて書いているときは第1の変数に関する偏微分は$\PDC{f\kakko{\tcol{t},\ycol{y}}}{\tcol{t}}{\ycol{y}}$になる。
1変数関数の極大・極小点では導関数が0になったが、多変数(ここでは「2変数」のみを扱う)関数の場合も極大極小点で導関数が0になるのは同じである。ただし、多変数なら「微分の方向」があるので「ある方向では0だが、別の方向では0でない」ということが起こりえる。
次の図に示したのは$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2+\ycol{y}^2,-\xcol{x}^2-\ycol{y}^2,\xcol{x}^2-\ycol{y}^2$の三つの関数の3次元グラフで、どの場合も原点においてどの方向の微分も0であるが、二階微分の値の正負が違う。
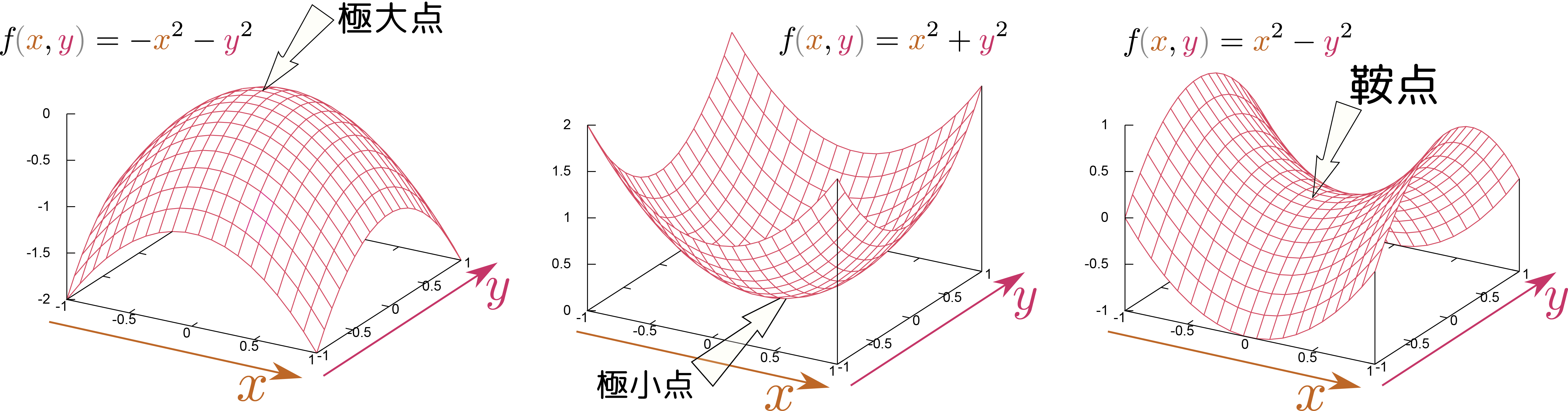
どの方向に対しても一階微分が0で二階微分が負なら、それは極大点である。逆に、どの方向に対しても一階微分が0で二階微分が正なら、それは極小点である(ここまでは1変数の時の素直な拡張である)。多変数で現れる新しい状況として「一階微分はどの方向に対しても0であるが、二階微分の正負は方向により異なる」という場合があり、この場合は(図に示したように馬の鞍の形なので)「鞍点(saddle point)」と呼ぶ。
上では比較的単純な例を提示したので、$\PPD{f}{\xcol{x}}$と$\PPD{f}{\ycol{y}}$の正負を見て場合分けできたが、2変数関数の二階微分はもう一つ、$\PPDD{f}{\xcol{x}}{\ycol{y}}$もある(上の例では全て$\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}\partial \ycol{y}}=0$なので気にしなくてもよかった)。