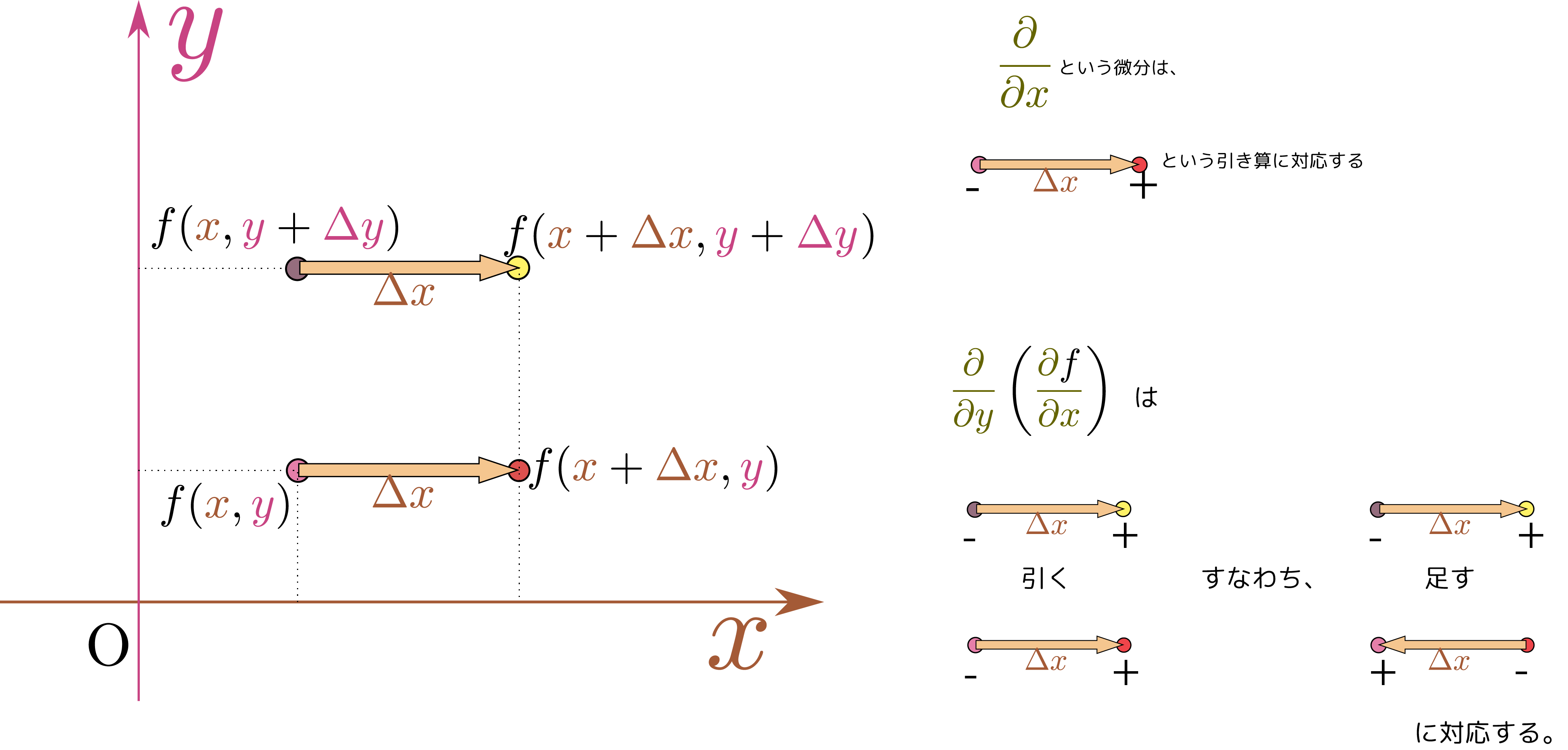
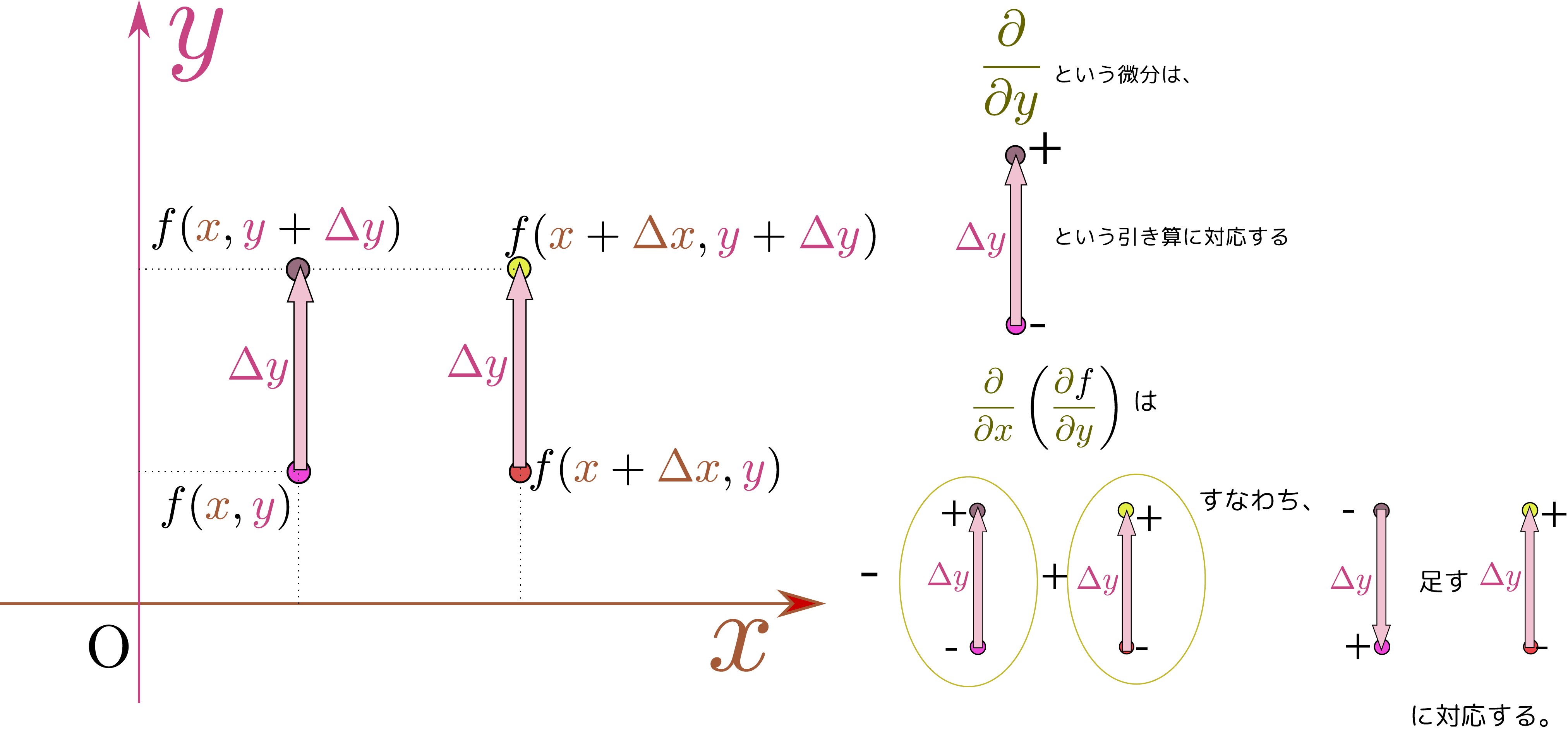
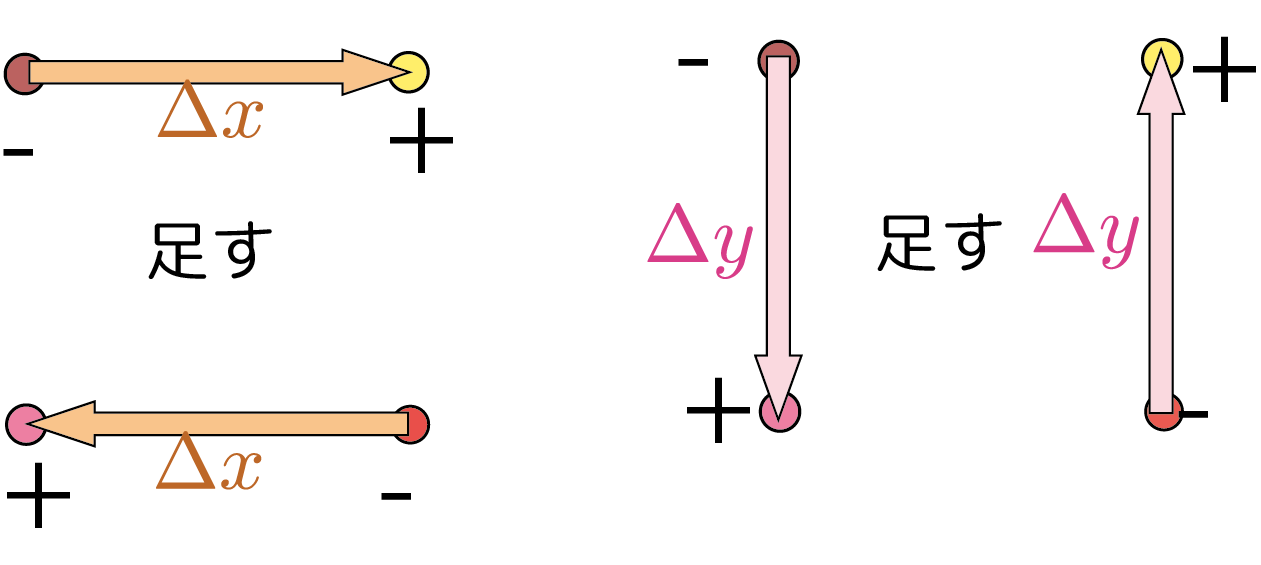偏微分と極大・極小
多変数関数のグラフ
先週は簡単な例で2変数関数の極大・極小を考えた。その例では、$\PPD{f}{\xcol{x}}$と$\PPD{f}{\ycol{y}}$の正負を見て場合分けできたが、2変数関数の二階微分はもう一つ、$\PPDD{f}{\xcol{x}}{\ycol{y}}$もある(これまでの例では全て$\opcol{{\partial^2 \kuro{f}\over \partial \xcol{x}\partial \ycol{y}}}=0$なので気にしなくてもよかった)。
逆に$\PPDD{f}{\xcol{x}}{\ycol{y}}\neq0$である例として、$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y}$の原点$(0,0)$を考えてみると、この場所も鞍点になっている実はこのグラフは$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2-\ycol{y}^2$を${\pi\over 4}$だけ回転して、少し高さを調整したものになっている。。
↓のような曲面を作るため、ストッキングを持っていって曲げたり伸ばしたりしながら授業した。
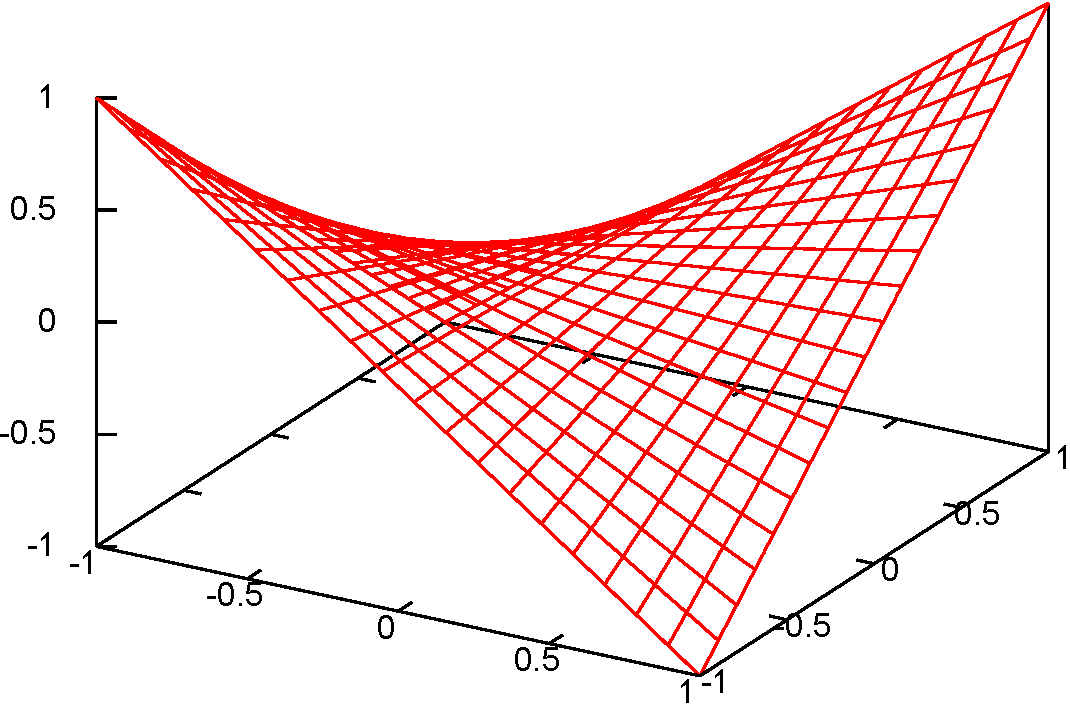
一般の2変数関数で、一階微分が全て0である点(このような点は「停留点」と呼ぶ停留点の中には、極大点と極小点と鞍点が含まれる。)が見つかったとして、その点が極大なのか極小なのかそれとも鞍点なのかを知りたい「別にそんなの知りたくない」って?---この関数がたとえば貴方の所有している財産の価値だったら、「ここが極大かどうか」を知りたくならないかな?場合は、テイラー展開の2次の項を調べる必要がある。
$(a,b)$が停留点とすればそこで一階微分は0だから、$(\xcol{x}-a)=\xcol{\Delta x},(\ycol{y}-b)=\ycol{\Delta y}$と書けば、 \begin{equation} f\kakko{\xcol{x},\ycol{y}} =f\kakko{a,b} +\goverbrace{\underbrace{{1\over 2}\PPD{f}{\xcol{x}}}_a(\xcol{\Delta x})^2 +\underbrace{\PPDD{f}{\xcol{x}}{\ycol{y}}}_b\xcol{\Delta x}\ycol{\Delta y} +\underbrace{{1\over 2}\PPD{f}{\ycol{y}}}_c(\ycol{\Delta y})^2}^{曲がり具合を表現する部分} +\cdots \end{equation} となる。3次以上の項$(\cdots)$は省略した。式に示したように、係数を以下$a,b,c$で表す。
上の「曲がり具合を表現する部分」がどのような$\xcol{\Delta x},\ycol{\Delta y}$に対しても正であるならばこの点は極小点、逆に常に負ならば極大点である。正にも負にもなる場合は鞍点だと言える(他の可能性としては正、負ではなく0以上や0以下という可能性もある)。この式は \begin{equation} a(\xcol{\Delta x})^2 + b\xcol{\Delta x}\ycol{\Delta y}+c(\ycol{\Delta y})^2 =\underbrace{(\ycol{\Delta y})^2}_{常に正}\underbrace{ \left( a\left({\xcol{\Delta x}\over\ycol{\Delta y} }\right)^2 +b{\xcol{\Delta x}\over\ycol{\Delta y} }+c \right)}_{この部分の正負が問題} \end{equation} となるから、$\tcol{t}={\xcol{\Delta x}\over\ycol{\Delta y}}$とすれば後は「二次式$a\tcol{t}^2+b\tcol{t}+c$の正負を場合分けせよ」という問題$\tcol{t}={\xcol{\Delta x}\over\ycol{\Delta y} }$の変域は実数全体である。$\xcol{\Delta x}=a\cos\alpha,\ycol{\Delta y}=a\sin\alpha$と置けば、${\xcol{\Delta x}\over\ycol{\Delta y} }=\cot \alpha$となる。になり、
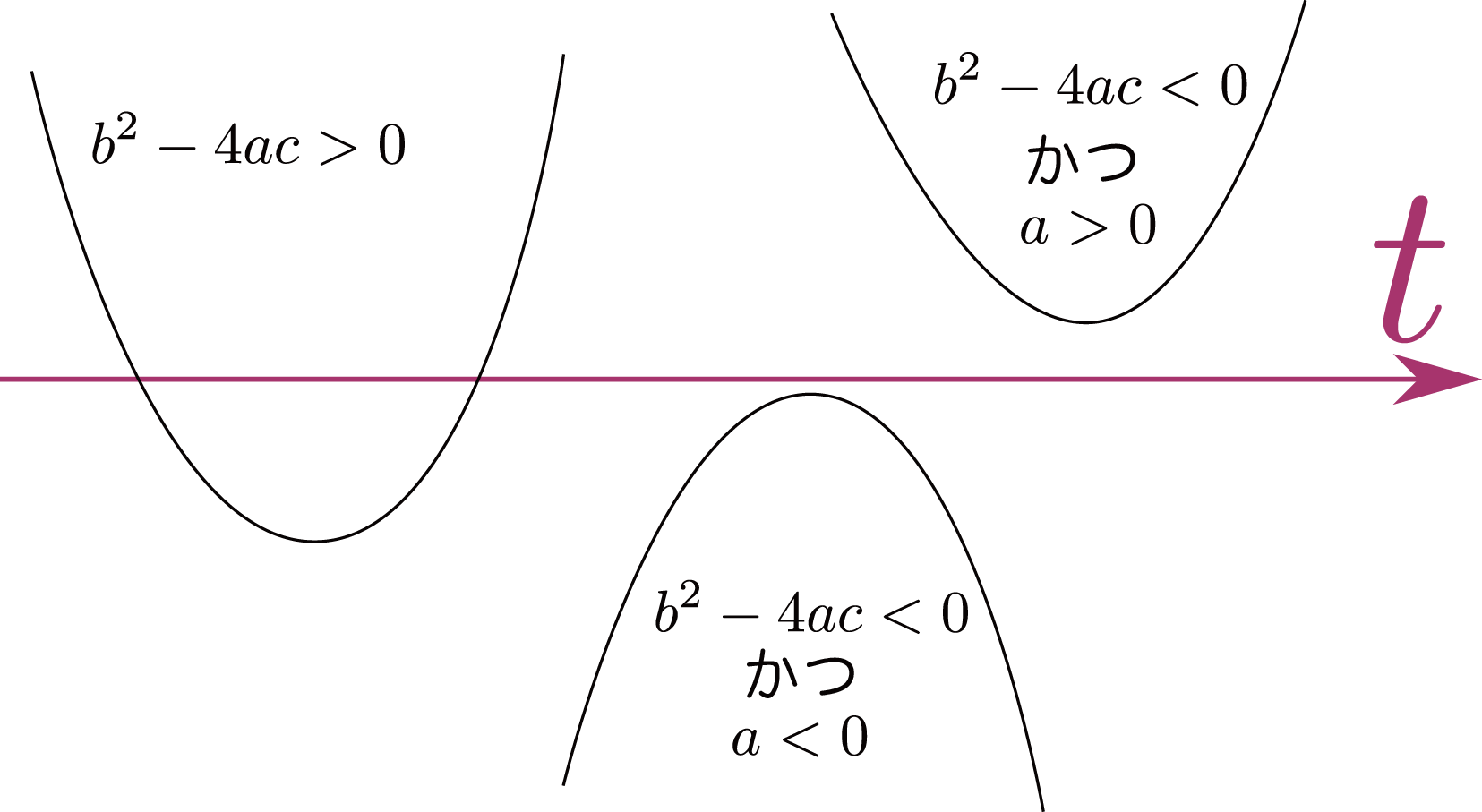
- $b^2-4ac>0$ の場合: 正にも負にもなる(鞍点)
- $b^2-4ac<0$ かつ $a>0$の場合: 常に正(極小点)
- $b^2-4ac<0$ かつ $a<0$の場合: 常に負(極大点)
のように二次方程式の判別式を使うこととで状況を分類することができる$b^2-4ac=0$の場合は省略したが、正(もしくは負)が0以上(もしくは0以下)になるという違いである。。
この判別式$b^2-4ac$というのは実は$\left(\begin{array}{cc}\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}^2}&\opcol{\partial^2 \kuro{f}\over \partial \xcol{x}\partial {\ycol{y}}}\\[3mm]\opcol{\partial^2 \kuro{f}\over \partial {\ycol{y}}\partial \xcol{x}}&\opcol{\partial^2 \kuro{f}\over \partial {\ycol{y}}^2}\end{array}\right)$という行列(「ヘッセ行列」と呼ぶ)の行列式の$-4$倍である。行列の形で書くと、3変数以上の場合にも拡張できる(作り方のルールは類推できるだろう)。