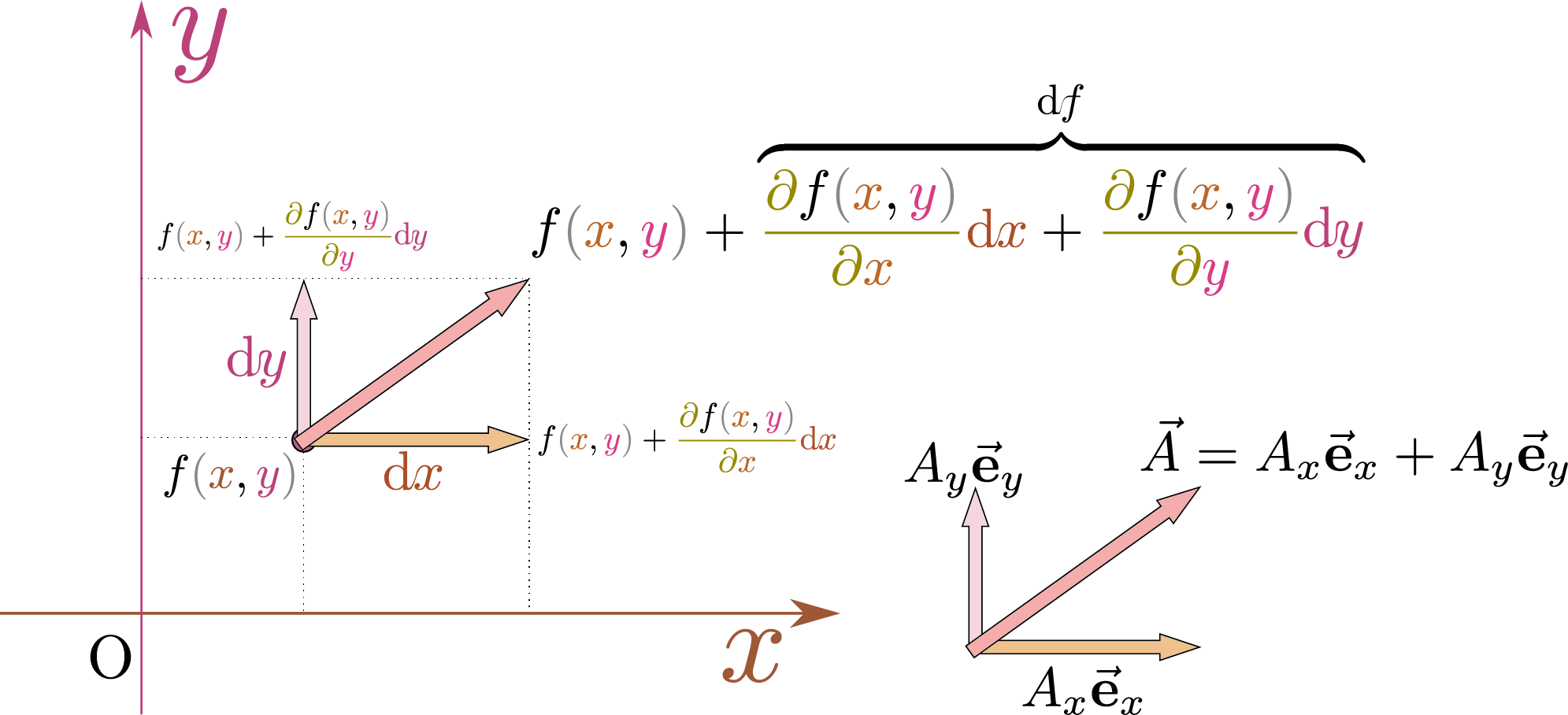全微分と偏微分
「関数$f\kakko{\xcol{x},\ycol{y}}$の微小変化」を表す量は、以下の式のように書ける。
関数$f\kakko{\xcol{x},\ycol{y}}$の全微分
\begin{equation}
\mathrm df\kakko{\xcol{x},\ycol{y}}=\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\coldx+\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\coldy\label{koregazenbibun}
\end{equation}
この$\diff\left( ? \right)$という形の式を「?の全微分(exact differential)」と言う。前に「偏微分には方向がある」と述べたが、上の式は「$\xcol{x}$方向の偏微分係数$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$」と「$\ycol{y}$方向の偏微分係数$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}$」の二つを含む。
全微分の式は(常微分のとき\文中式{$f\kakko{\xcol{x}}$の変化が$f'\kakko{\xcol{x}}\coldx$と書けた}のと同様に)
$f\kakko{\xcol{x},\ycol{y}}$に起こる変化のうち、
- $\xcol{x}$の変化によって起こる変化は$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\coldx$と書け、
- $\ycol{y}$の変化によって起こる変化は$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\coldy$と書ける。
というふうに「読む」べきである。
$f\kakko{\xcol{x},\ycol{y}}$の全微分のうち$\coldx$の係数である$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$を取り出したもの($\ycol{y}$方向も同様)が「偏微分」である。ベクトルを$\vec A=A_x\vec{\mathbf e}_x+A_y\vec{\mathbf e}_y$と$\xcol{x}$成分と$\ycol{y}$成分に分けて表現する($\vec A$の$\xcol{x}$成分が$A_x$、$\vec A$の$\xcol{y}$成分が$A_y$)のと同様に、$\mathrm df\kakko{\xcol{x},\ycol{y}}$の$\xcol{x}$成分(のようなもの)が$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$、$\mathrm df\kakko{\xcol{x},\ycol{y}}$の$\ycol{y}$成分(のようなもの)が$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}$}であると思ってよい。
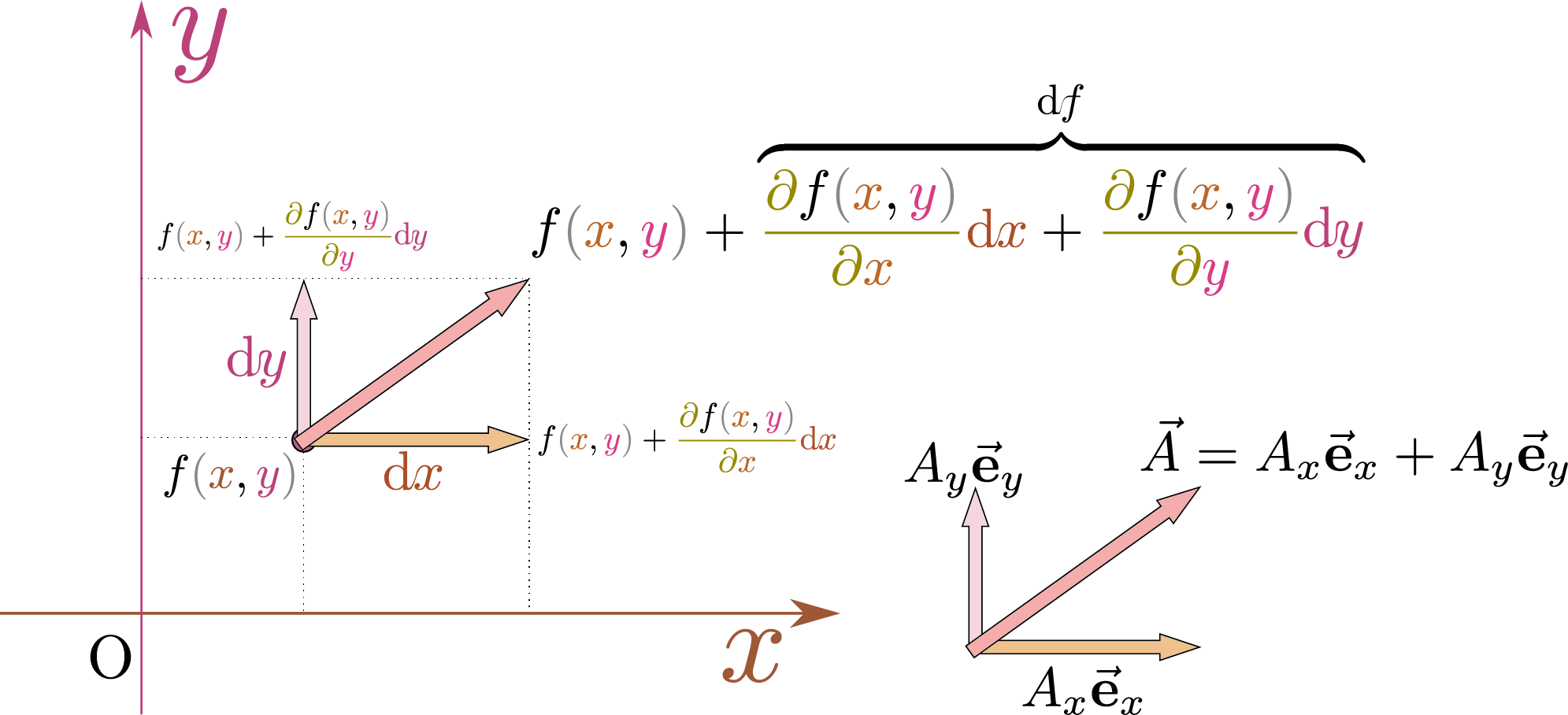
全微分を考えることの意義の一つとして、「全微分は変数の取り方によらない」ということがある。偏微分$\PD{f}{\xcol{x}},\PD{f}{\ycol{y}}$は我々1がどのように座標(たとえば$\xcol{x},\ycol{y}$)を選んだかによって変わる量である(後で、これを使って偏微分の関係を導こう)が、全微分として組み合わされた$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\coldx+\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\coldy$は座標を変えても変わらない量になる(もともと、$f\kakko{\xcol{x},\ycol{y}}$の変化量という意味のある量だから)。
全微分は座標に依らない。しかしその一部を取り出した偏微分(たとえば$\xcol{x}$方向の偏微分は$\PDC{f}{\xcol{x}}{\ycol{y}}$)は座標の取り方によって変わる($\xcol{x}$座標や$\ycol{y}$座標が変わってしまえば、$\PDC{f}{\xcol{x}}{\ycol{y}}$も変わらずにいられない)。
これは、「ベクトル$\vec A$は座標系によらずに(人間がどんな座標系を取るかに関係なく)存在するが、それを$\vec A=A_x\vec{\mathbf e}_x+A_y\vec{\mathbf e}_y$と表現したときの$\xcol{x}$成分$A_x$や$\ycol{y}$成分$A_y$は座標系に依存した量である」のと同様である。
たとえば横$\xcol{x}$、縦$\ycol{y}$の長方形の面積$\rcol{S}=\xcol{x}\ycol{y}$の全微分はライプニッツ則により
\begin{equation}
\mathrm dS=\underbrace{\coldx \ycol{y}}_{\xcol{x}を微分した項}+ \underbrace{\xcol{x}\coldy}_{\ycol{y}を微分した項}
\end{equation}
となる。面積は、$\xcol{x}$が$\coldx$増加すれば、$\ycol{y}\coldx$だけ、$\ycol{y}$が$\coldy$増加すれば、$\xcol{x}\coldy$だけ増加することを上の式は表している。
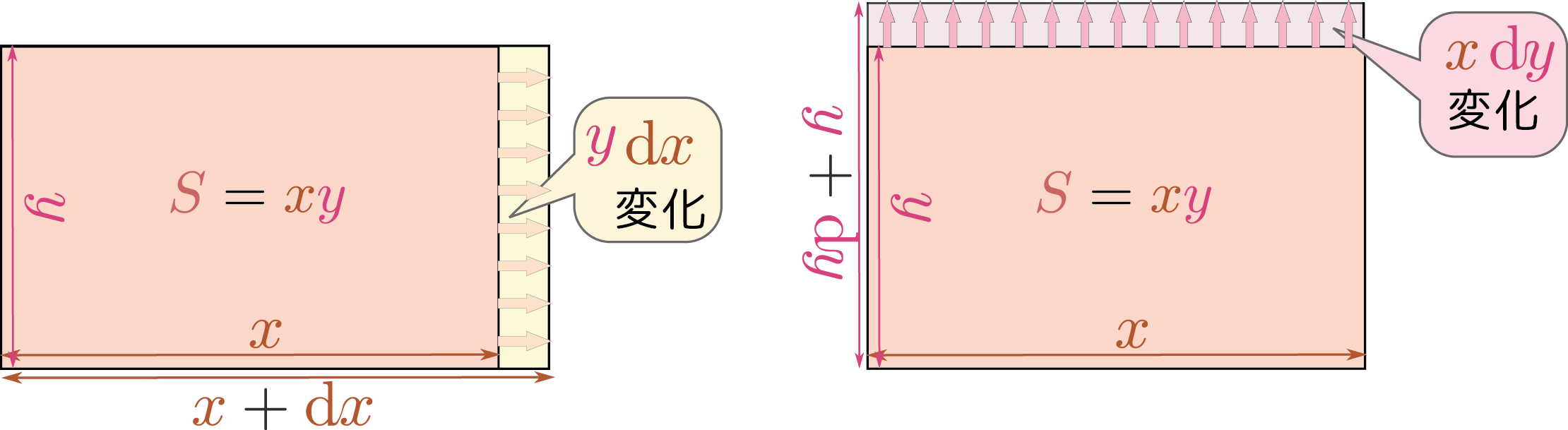
数式で表現すれば、$\PDC{(\xcol{x}\ycol{y})}{\xcol{x}}{\ycol{y}}=\ycol{y}$と、$\PDC{(\xcol{x}\ycol{y})}{\ycol{y}}{\xcol{x}}=\xcol{x}$ということになる。
全微分が0になる条件
ある関数の全微分が0になる条件を知ることが大切な場合があるので、その例について話しておこう。
例1:$S=\xcol{x}\ycol{y}$
上でも考えた$\rcol{S}=\xcol{x}\ycol{y}$を考えよう。この$\rcol{S}$の全微分が0になるということは、すなわち$\rcol{S}$が一定だということである。
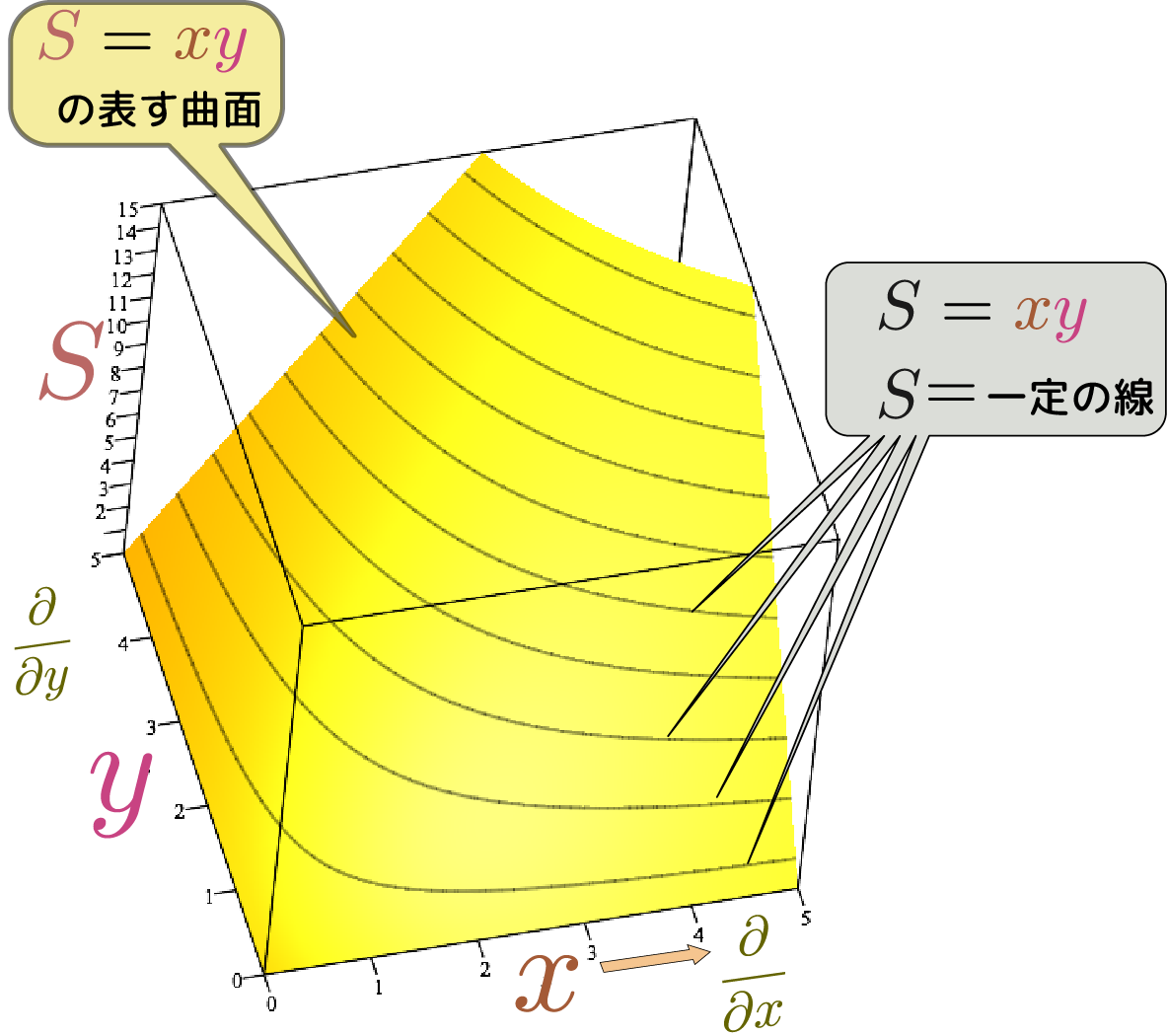
$\rcol{S}$が一定という条件がついていない場合を上のように図で表現すると、$\xcol{x},\ycol{y},\rcol{S}$という3次元座標(自由度3)に$\rcol{S}=\xcol{x}\ycol{y}$という制限がつくことで、2次元の面(曲面)が表現されている。すなわち、$\rcol{S}$が自由な値を取るとき、$\rcol{S}=\xcol{x}\ycol{y}$が表すのは2次元の曲面である(自由度2)。$\rcol{S}$が一つの値$S$に固定(条件$S(定数)=\xcol{x}\ycol{y}$)されると、自由度はさらに一つ減り1になる。結果として、$S(定数)=\xcol{x}\ycol{y}$が表すのは1次元的な線(曲線)になる。
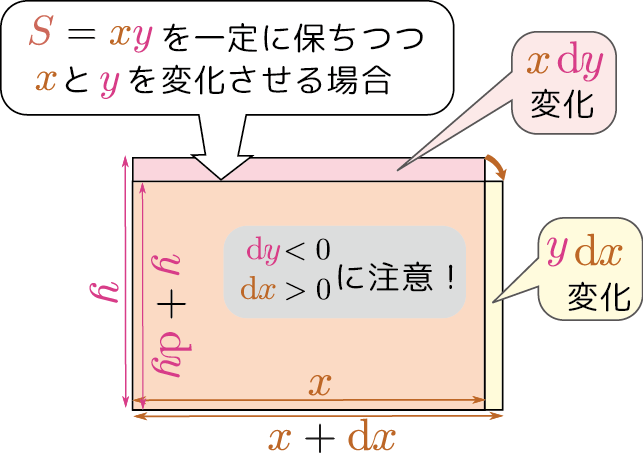
変数である$\rcol{S}$に対する$\rcol{S}=\xcol{x}\ycol{y}$が「山の地表面」を表すと考えると、定数となった$S$に対する$S=\xcol{x}\ycol{y}$が表現するのはいわば「等高線」である。それも図に示した。$\rcol{S}$を一定にしたことにより、1変数関数($\xcol{x}$と$\ycol{y}$のどちらかが独立変数で、もう片方が従属変数)となっている。 面積を一定に$\rcol{S}=\xcol{x}\ycol{y}=C(定数)$を保ちつつ、すなわち$\rcol{ S}$の全微分を0($\dS=0$)にしつつ$\xcol{x}$と$\ycol{y}$を変化させる様子を図示すれば右の図のようになる。このときの$\coldx$と$\coldy$は0ではないが、$\coldx \ycol{y}+\xcol{x}\coldy=0$という関係を持つ。この式は${\coldy\over \coldx}=-{\ycol{y}\over \xcol{x}}$または$\coldx:\coldy=\xcol{x}:(-\ycol{y})$と書き直すこともできる。
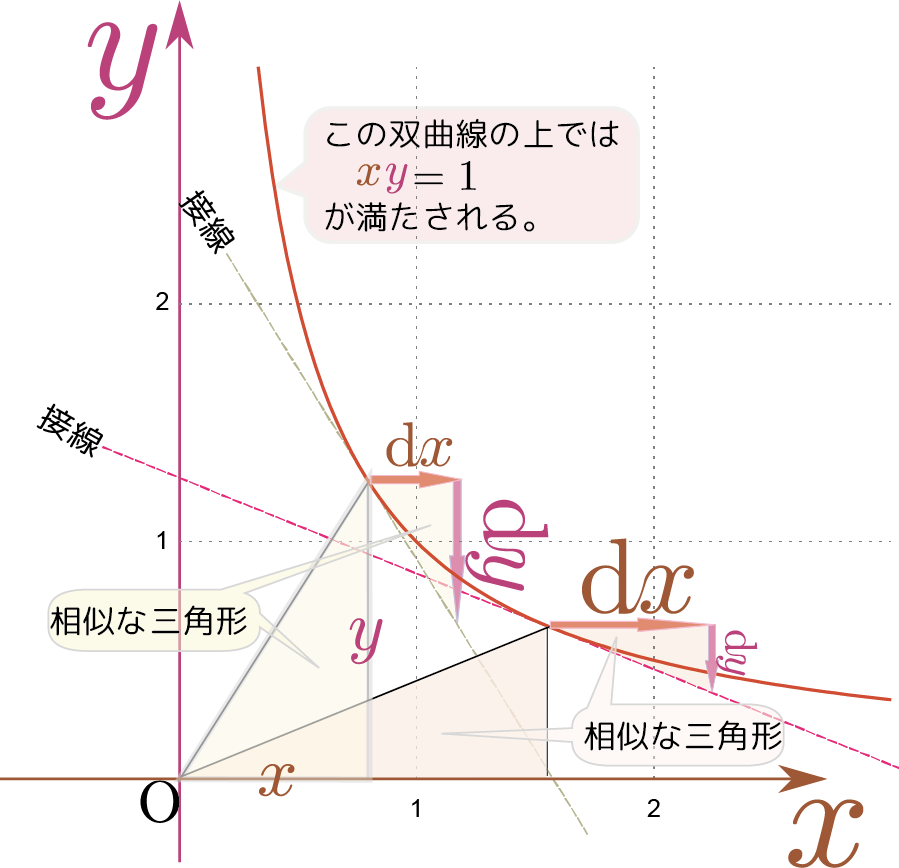
$\ycol{y}\coldx + \xcol{x}\coldy=0$をグラフで表現したのが上の図である。定数である$S$を一つ指定することで線(この場合は双曲線になる)が引ける。ここでは$\xcol{x}\ycol{y}=1$のグラフのみを描いた。グラフ上に表現したように、$\coldx:\coldy=\xcol{x}:(-\ycol{y})$となっていて、$(\xcol{x},\ycol{y})$を斜辺とする直角三角形と$(\coldx,\coldy)$を斜辺とする直角三角形は、上下をひっくり返した相似形である。
$\ycol{y}\coldx + \xcol{x}\coldy=0$から$\xcol{x}\ycol{y}=一定$を求めるのは、各点における接線の傾きからこの双曲線を導き出す計算であり、逆に「全微分を求める」というのは双曲線から接線の傾きを($\coldx$と$\coldy$の比の形で)求める計算だったと思ってもよい。
例2:$R=\sqrt{\xcol{x}^2+\ycol{y}^2}$
$\xcol{x}$と$\ycol{y}$が$\sqrt{\xcol{x}^2+\ycol{y}^2}$が一定であるという関係を持っている場合、$\xcol{x}$と$\ycol{y}$それぞれの変化量である$\coldx$と$\coldy$も独立ではない。$\sqrt{\xcol{x}^2+\ycol{y}^2}=R\kakko{一定}$を保ちつつ(グラフ上では、原点を中心とする半径$R$の円の上に乗りつつ)変化させた様子を描いたのが次の図である。
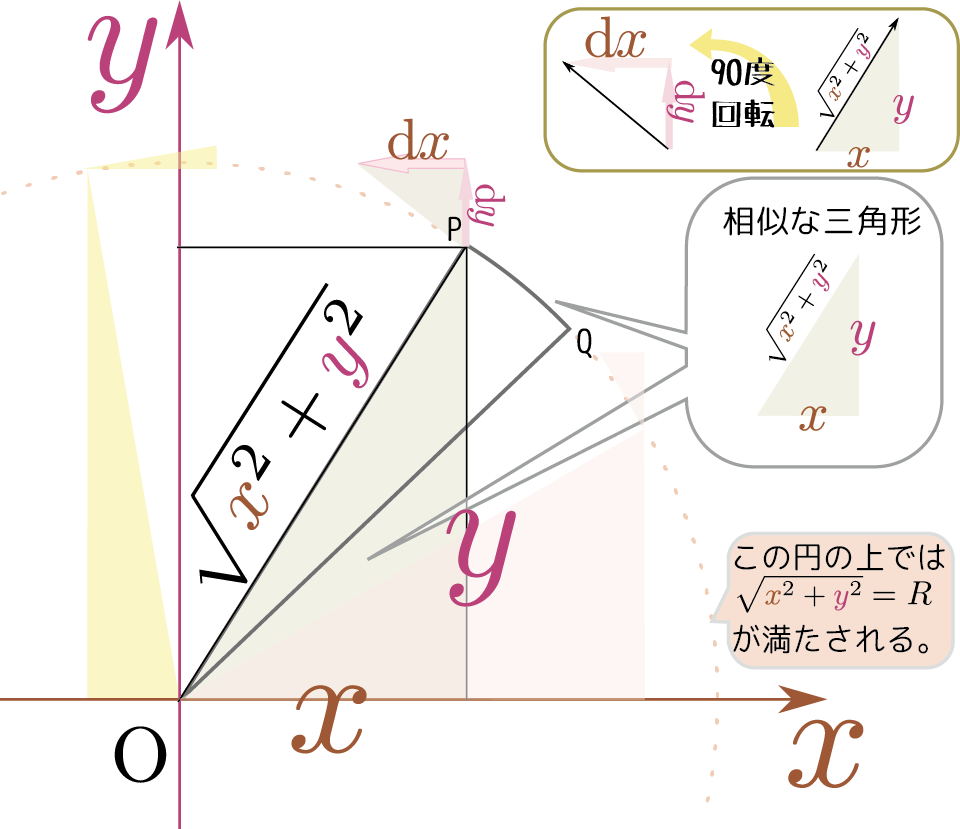
右の相似な三角形に注意すると、$\coldx$と$\coldy$の間に
\begin{equation}
\xcol{x}\coldx+\ycol{y}\coldy=0\label{xdxydyzero}
\end{equation}
という式が出る。一方、$\sqrt{\xcol{x}^2+\ycol{y}^2 }$の全微分が0であるという条件は
\begin{equation}
\goverbrace{{\xcol{x}\over\sqrt{\xcol{x}^2+\ycol{y}^2 }}}^{\PD{\sqrt{\xcol{x}^2+\ycol{y}^2 }}{\xcol{x}}}\coldx
+ \goverbrace{{\ycol{y}\over\sqrt{\xcol{x}^2+\ycol{y}^2 }}}^{\PD{\sqrt{\xcol{x}^2+\ycol{y}^2 }}{\ycol{y}}}\coldy=0
\end{equation}
という、本質的に(両辺に$\sqrt{\xcol{x}^2+\ycol{y}^2 }$を掛ければ)上と同じ式になる。
この$\xcol{x}\coldx+\ycol{y}\coldy=0$という式は、$(\xcol{x},\ycol{y})\cdot \left(\coldx,\coldy\right)=0 $のように$\left(\coldx,\coldy\right)$というベクトル(図の$\overrightarrow{\rm PQ}$)と$\left(\xcol{x},\ycol{y}\right)$というベクトル(図の$\overrightarrow{\rm OP}$)の内積が0(垂直)という式だと解釈することもできる。これは「円の接線」の性質に合致している。つまりこの$\sqrt{\xcol{x}^2+\ycol{y}^2}$を一定としての全微分は「$\thetacol{\theta}$方向の微分」になる。
以上、二つの例を示したが、全微分$=0$の条件が「$\xcol{x}$と$\ycol{y}$の間にある関係式が成り立つ」ことであり、「$\xcol{x}$-$\ycol{y}$グラフの上の曲線で表現される」ことでもあるという点を理解して欲しい。つまり2変数を含むに対する全微分$=0$の条件は関数を一つ決めているのであり、これも一種の微分方程式である。
ある常微分方程式${\coldy\over \coldx}=f\kakko{\xcol{x},\ycol{y}}$を$P\kakko{\xcol{x},\ycol{y}}\coldx + Q\kakko{\xcol{x},\ycol{y}}\coldy =0$と変形して、なんらかの計算の後に$\diff\left(なんとか\right)=0$の形にまとめ直すことができれば(すなわち、全微分$=0$の形に書き直すことができれば)、$なんとか=定数$と積分ができる。
つまり、$P\kakko{\xcol{x},\ycol{y}}\coldx + Q\kakko{\xcol{x},\ycol{y}}\coldy$を$\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\coldx+\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\coldy$の形に直す、という方針で微分方程式を解くのである。
以下の微分方程式を$\diff (なんとか)$の形にして解いてみよう。
$$
{\ycol{y}\over \xcol{x}}\coldx + (\log\xcol{x})\coldy=0
$$
これは${\ycol{y}\over \xcol{x}}=\PD{(\ycol{y}\log\xcol{x})}{\xcol{x}}$と$\log\xcol{x}=\PD{(\ycol{y}\log\xcol{x})}{\ycol{y}}$に気づけば、
$$
\diff\left(\ycol{y}\log\xcol{x}\right)=0
$$
と変形できることに気づく。
ゆえに解は
$$
\ycol{y}\log\xcol{x}=C(定数)
$$
である。
上の場合は少し探すと答が見つかったが、実はこれが「運が良かった」のである。たとえば、
$$
-\ycol{y}\coldx+\coldy=0
$$
という微分方程式をなにかの全微分にしょうとしても、うまくいかないだろう。実はこの式は$\E^{-\xcol{x}}$を掛けて
$$
- \ycol{y}\E^{-\xcol{x}}\coldx + \E^{-\xcol{x}}\coldy
$$
と直すと、全微分形
$$
\diff\left(\ycol{y}\E^{-\xcol{x}}\right)=0
$$
になる。
以上の例から、解ける微分方程式であっても、単に$P\coldx+Q\coldy=0$の形にしただけでは全微分形にはなっていないこともあることがわかる。しかし、適当に何らかの関数を掛けてやることで全微分形に直していくことができる場合もある。
以下のような問題を考えよう。
式$P\kakko{\xcol{x},\ycol{y}}\coldx+Q\kakko{\xcol{x},\ycol{y}}\coldy$は、何かの式の全微分だろうか?
ある関数$U\kakko{\xcol{x},\ycol{y}}$があったとすると、その全微分は
\begin{equation}
\underbrace{ \PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}_{P\kakko{\xcol{x},\ycol{y}}?}\coldx
+\underbrace{ \PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}_{Q\kakko{\xcol{x},\ycol{y}}?}\coldy=0
\end{equation}
だから、
\begin{equation}
\PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}=P\kakko{\xcol{x},\ycol{y}},~~~
\PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=Q\kakko{\xcol{x},\ycol{y}}
\end{equation}
となるような$U\kakko{\xcol{x},\ycol{y}}$は見つけることができればよい。問題は、$P\kakko{\xcol{x},\ycol{y}},Q\kakko{\xcol{x},\ycol{y}}$の形によっては解が見つからないことである。
そこで、$U\kakko{\xcol{x},\ycol{y}}$が見つかるための必要条件を求めておこう(これがあれば「あ、この場合は全微分にできない」ということがすぐわかる)。微分可能な関数$f\kakko{\xcol{x},\ycol{y}}$の偏微分が持つべき性質として、「偏微分の交換可能性」があった。その式から、
\begin{equation}
Uが存在する。\Rightarrow \biggl(\opcol{\partial \over \partial x}\underbrace{\PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}_{Q\kakko{\xcol{x},\ycol{y}}}\biggr)_{\!\!\ycol{y}}= \biggl(\opcol{\partial \over \partial y}\underbrace{\PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}_{P\kakko{\xcol{x},\ycol{y}}}\biggr)_{\!\!\xcol{x}}
\end{equation}
がわかる。よって
\begin{equation}
\PDC{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=
\PDC{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}~~~または~~~
\PDC{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}-
\PDC{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=0\label{sekibunkanou}
\end{equation}
は$\diff\left(U\kakko{\xcol{x},\ycol{y}}\right)=P\kakko{\xcol{x},\ycol{y}}\coldx+Q\kakko{\xcol{x},\ycol{y}}\coldy$となる$U$が存在するための条件となる。
たとえばさっきの${\ycol{y}\over \xcol{x}}\coldx + (\log\xcol{x})\coldy$なら、$\PD{{\ycol{y}\over \xcol{x}}}{\ycol{y}}={1\over\xcol{x}},\PD{(\log\xcol{x})}{\xcol{x}}={1\over\xcol{x}}$となって成立。
一方、$-\ycol{y}\coldx+\coldy$では、$\PD{(-\ycol{y})}{\ycol{y}}=-1,\PD{(1)}{\xcol{x}}=0$で不成立。
この条件の詳細については、次回。