全微分
微分方程式というと、 $$ {\coldy\over\coldx}=f\kakko{\xcol{x},\ycol{y}} $$ という形が多いが、これは「微小変化$\coldx$」と「微小変化$\coldy$」の比(の極限)が$f\kakko{\xcol{x},\ycol{y}}$になる、という意味だから、 $$ P\kakko{\xcol{x},\ycol{y}}\coldx +Q\kakko{\xcol{x},\ycol{y}}\coldy=0 $$ という形に書き直すことができる。
この式の左辺が実は$U\kakko{\xcol{x},\ycol{y}}$の「全微分」すなわち、 $$ \diff U\kakko{\xcol{x},\ycol{y}}=\PD{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}\coldx+\PD{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\coldy $$ という形になっていれば、 $$ U\kakko{\xcol{x},\ycol{y}}=定数 $$ という形で微分方程式が解けてしまう、というのが全微分を使った微分方程式の解き方である。
ただし、このようにできるためには$P\kakko{\xcol{x},\ycol{y}}$と$Q\kakko{\xcol{x},\ycol{y}}$が「ある条件」を満たさなくてはいけない、というところまでを前回話した。
いくつかの微分方程式(これまでやったもの)を表にしてみよう。
| (1) | (2) | (3) | (4) | (5) |
| 微分方程式 | 変数分離した形 | 解 | 一定となる量$U$ | $U$の全微分 |
| ${\coldy\over \coldx}=-{\xcol{x}\over \ycol{y}}~~~~$ | $\xcol{x}\coldx+\ycol{y}\coldy=0$ | $\xcol{x}^2+\ycol{y}^2=R^2$ | $\xcol{x}^2+\ycol{y}^2$ | $2\xcol{x}\coldx+2\ycol{y}\coldy$ |
| ${\coldy\over \coldx}=-{\ycol{y}\over \xcol{x}}$ | ${1\over \xcol{x}}\coldx+{1\over \ycol{y}}\coldy =0$ | $\ycol{y}={C\over \xcol{x}}$ | ${\xcol{x}\ycol{y}}$ | $ \ycol{y}\coldx+ \xcol{x}\coldy$ |
| ${\coldy\over \coldx}={\ycol{y}\over \xcol{x}}$ | $- {1\over \xcol{x}}\coldx+{1\over \ycol{y}}\coldy =0$ | $\ycol{y}=C\xcol{x}$ | ${\ycol{y}\over \xcol{x}}$ | $-{\ycol{y}\over \xcol{x}^2}\coldx+ {\coldy\over \xcol{x}}$ |
| ${\coldy\over \coldx}=\ycol{y}$ | $-\coldx+{1\over \ycol{y}}\coldy=0$ | $\ycol{y}=C\E^{\xcol{x}}$ | $\ycol{y}\E^{-\xcol{x}}$ | $ - \ycol{y}\E^{-\xcol{x}}\coldx + \E^{-\xcol{x}}\coldy$ |
ここで、
というのが変数分離を使って解く微分方程式の解法だが、
という微分方程式の解法も有り得るこの場合、変数分離不可能でも解ける可能性が出てくる。。
この「全微分形に直す」という解法を考えるために、上の例それぞれの場合で(2)と(5)の違いを見てみよう。
${\coldy\over \coldx}=-{\xcol{x}\over \ycol{y}}$の場合: (5)は(2)の2倍。
${\coldy\over \coldx}=-{\ycol{y}\over \xcol{x}}$の場合}: (5)は(2)の${\xcol{x}\ycol{y}}$倍。
${\coldy\over \coldx}={\ycol{y}\over \xcol{x}}$の場合: (5)は(2)の${\ycol{y}\over \xcol{x}}$倍。
${\coldy\over \coldx}=\ycol{y}$の場合: (5)は(2)の${1\over \ycol{y}\E^{-\xcol{x}}}$倍。
以上の例から、解ける微分方程式であっても、単に$P\coldx+Q\coldy=0$の形にしただけでは全微分形にはなっていないこともあることがわかる。
しかし、適当に何らかの関数を掛けてやることで全微分形に直していくことができる場合もある常にできるとは限らないが、これができるならこのやり方で解ける微分方程式だったということ。。
したがって微分方程式を「全微分形にする」という方針で解こうとするのであれば、方程式に適切な関数を掛けるという操作が必要になりそうである。たとえば、 \begin{equation} f'\kakko{\xcol{x}}\ycol{y}\coldx+f\kakko{\xcol{x}}\coldy=0 \end{equation} のような微分方程式があったならば、 \begin{equation} \diff \left(f\kakko{\xcol{x}}{\ycol{y}}\right)=0 \end{equation} という形にまとめていくことで解いていくことができそうだ。
積分可能条件
以下のような問題を考えよう。
たとえば我々はすでに$\ycol{y}\coldx+\xcol{x}\coldy$は$\xcol{x}\ycol{y}$の全微分であることや、${\xcol{x}\over \sqrt{\xcol{x}^2+\ycol{y}^2}}\coldx+{\ycol{y}\over \sqrt{\xcol{x}^2+\ycol{y}^2}}\coldy$が$\sqrt{\xcol{x}^2+\ycol{y}^2}$の全微分であることを知っている。では今ここで$なんとか\kakko{\xcol{x},\ycol{y}}\coldx+かんとか\kakko{\xcol{x},\ycol{y}}\coldy$という式を見せられて、「これは○○の全微分である」とわかるだろうか?---たとえば$\xcol{x}\ycol{y}\coldx+\xcol{x}^2\coldy$という式は、何かの全微分になっているだろうか?
今から微分方程式を解こうとしているとき、「この式が全微分に直せる」ということがすぐに判定できれば、たいへん有利なので、この問題の答えとなる、ある条件を以下で求めたい。
ある関数$U\kakko{\xcol{x},\ycol{y}}$があったとすると、その全微分は \begin{equation} \underbrace{ \PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}_{P\kakko{\xcol{x},\ycol{y}}?}\coldx +\underbrace{ \PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}_{Q\kakko{\xcol{x},\ycol{y}}?}\coldy=0 \end{equation} だから、 \begin{equation} \PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}=P\kakko{\xcol{x},\ycol{y}},~~~ \PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=Q\kakko{\xcol{x},\ycol{y}} \end{equation} となるような$U\kakko{\xcol{x},\ycol{y}}$は見つけることができればよい。問題は、$P\kakko{\xcol{x},\ycol{y}},Q\kakko{\xcol{x},\ycol{y}}$の形によっては解が見つからないことである。
そこで、$U\kakko{\xcol{x},\ycol{y}}$が見つかるための必要条件を求めておこう(これがあれば「あ、この場合は全微分にできない」ということがすぐわかる)。微分可能な関数$f\kakko{\xcol{x},\ycol{y}}$の偏微分が持つべき性質として、「偏微分の交換可能性」があった。その式から、 \begin{equation} Uが存在する。\Rightarrow \biggl(\opcol{\partial \over \partial x}\underbrace{\PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}}_{Q\kakko{\xcol{x},\ycol{y}}}\biggr)_{\!\!\ycol{y}}= \biggl(\opcol{\partial \over \partial y}\underbrace{\PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}}_{P\kakko{\xcol{x},\ycol{y}}}\biggr)_{\!\!\xcol{x}} \end{equation} がわかる。よってこの対偶「$P\Rightarrow Q$」に対して「$Qでない\Rightarrow Pでない$」をその対偶と呼ぶ。ある命題が正しければその対偶も正しい。を取れば、 $$ \PDC{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}- \PDC{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\neq0\Rightarrow U$は存在しない $$ となる。すぐ後で示すようにこの逆も成り立つので、
積分可能条件
\begin{equation} \PDC{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}= \PDC{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}~~~または~~~ \PDC{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}- \PDC{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=0\label{sekibunkanou} \end{equation} は$\diff\left(U\kakko{\xcol{x},\ycol{y}}\right)=P\kakko{\xcol{x},\ycol{y}}\coldx+Q\kakko{\xcol{x},\ycol{y}}\coldy$となる$U$が存在するための必要十分条件「$A$が$B$の必要十分条件である」とは$A\Rightarrow B$と$B\Rightarrow A$の両方が成り立つこと。である。
がわかる。この式は「積分可能条件(integrability condition)」と呼ばれる。
たとえば$\xcol{x}\ycol{y}\coldx+\xcol{x}^2\coldy$は、$P\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y},Q\kakko{\xcol{x},\ycol{y}}=\xcol{x}^2$であり$\underbrace{\PD{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}}_{\xcol{x}}-\underbrace{\PD{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}}_{2\xcol{x}}\neq0$なので、積分可能条件は満たされず、全微分ではない。
$\PDC{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}- \PDC{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=0$の、「$\ycol{y}$に関係する量である$Q$を$\xcol{x}$で微分したものと、$\xcol{x}$に関係する量である$P$を$\ycol{y}$で微分したものを引算する」という計算は、ベクトル解析で「rot」という名前で登場するもの($\ycol{y}$成分を$\xcol{x}$で微分したもの引く$\xcol{x}$成分を$\ycol{y}$で微分したものを含んでいる)と似た形をしている(まだ知らない人は今後のお楽しみに置いておこう)。同様の式が出てきて、それが0になった時は「積分可能になった($U$が求められる!)」とピンと来て欲しい。
ここまでで示したのは、$U$が存在$\Rightarrow$積分可能条件が満たされるのみである。
この逆積分可能条件が満たされる$\Rightarrow U$が存在するも成り立つことを示そう。そのためには実際に$U$を作ってみせればよい。
まず \begin{equation} U_誤\kakko{\xcol{x},\ycol{y}} =\int_{x_0}^{\xcol{x}}\coldt P\kakko{\tcol{t},\ycol{y}} +\int_{y_0}^{\ycol{y}} \coldt Q\kakko{\xcol{x},\tcol{t}}\label{Umachigai} \end{equation} は間違いである。一見「微分は積分の逆だからこれでOK」と思ってしまいがちだが、この$U_誤$を$\xcol{x}$で微分すると(第2項にも$\xcol{x}$があることに注意)、 \begin{equation} \PDC{U_誤\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}=P\kakko{\xcol{x},\ycol{y}} +\int \coldt \PDC{Q\kakko{\xcol{x},\tcol{t}}}{\xcol{x}}{\ycol{y}} \end{equation} となってしまって$\opcol{\partial \kuro{U}\over \partial x}=P\kakko{\xcol{x},\ycol{y}}$にならない。$\opcol{\partial \kuro{U}\over \partial x}=P\kakko{\xcol{x},\ycol{y}}$とするのに$U$に必要なのは第1項の$\int_{x_0}^{\xcol{x}}\coldt P\kakko{\tcol{t},\ycol{y}} $だけであって、これ以外に$\xcol{x}$の関数を付け加えては答があわなくなってしまう。付け加えてもよいのは$\ycol{y}$の関数のみである。
というわけで、$Q\kakko{\xcol{x},\ycol{y}}$を含む項を入れるのをやめて、 \begin{equation} U_試\kakko{\xcol{x},\ycol{y}}=\int_{x_0}^{\xcol{x}}\coldt P\kakko{\tcol{t},\ycol{y}}+f\kakko{\ycol{y}} \end{equation} という関数を試しに作ってみる。この関数は$\PDC{U_試\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}=P\kakko{\xcol{x},\ycol{y}}$を満たす(第2項の$f\kakko{\ycol{y}}$は$\xcol{x}$で偏微分すると消える)。次に$\ycol{y}$で微分してみよう。 \begin{equation} \PDC{U_試\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} =\int_{x_0}^{\xcol{x}}\coldt \PDC{P\kakko{\tcol{t},\ycol{y}}}{\ycol{y}}{\tcol{t}} +\opcol{\diff \kuro{f\kakko{\ycol{y}}}\over \kidy} \end{equation} となる($f\kakko{\ycol{y}}$の微分は偏微分にする必要はないことに注意)。
この結果は$Q\kakko{\xcol{x},\ycol{y}}$にならなくてはいけない。積分可能条件$\PDC{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=\PDC{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}$を($\xcol{x}$のところに$\tcol{t}$を代入し$\PDC{P\kakko{\tcol{t},\ycol{y}}}{\ycol{y}}{\tcol{t}}=\PDC{Q\kakko{\tcol{t},\ycol{y}}}{\tcol{t}}{\ycol{y}}$に変えてから)使うと、 \begin{equation} \PDC{U_試\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} =\int_{x_0}^{\xcol{x}}\coldt\PDC{Q\kakko{\tcol{t},\ycol{y}}}{\tcol{t}}{\ycol{y}} +\opcol{\diff \kuro{f\kakko{\ycol{y}}}\over \kidy} \end{equation} となる。ここでの$\PD{}{\tcol{t}}$という計算は「$\ycol{y}$を一定として」という前提のもとでの計算だから、$\ycol{y}$は定数とみなしてよい。よって、$\int_{x_0}^{\xcol{x}}\coldt\opcol{\diff \kuro{f\kakko{\tcol{t}}}\over \kidt}=f\kakko{\xcol{x}}-f\kakko{x_0}$という、定積分と原始関数の関係が偏微分に対しても同様に成り立って、 \begin{equation} \int_{x_0}^{\xcol{x}}\coldt\PDC{Q\kakko{\tcol{t},\ycol{y}}}{\tcol{t}}{\ycol{y}}=Q\kakko{\xcol{x},\ycol{y}}-Q\kakko{x_0,\ycol{y}} \end{equation} とすることができる($\tcol{t}$で微分してから$\tcol{t}$で定積分した、ということ)。これを使えば \begin{equation} \PDC{U_試(\xcol{x},\ycol{y})}{\ycol{y}}{\xcol{x}} =\int_{x_0}^{\xcol{x}}\coldt\PDC{Q\kakko{\tcol{t},\ycol{y}}}{\tcol{t}}{\ycol{y}} + \opcol{\diff \kuro{f\kakko{\ycol{y}}}\over \kidy}=Q\kakko{\xcol{x},\ycol{y}}\underbrace{-Q\kakko{x_0,\ycol{y}} +\opcol{\diff \kuro{f\kakko{\ycol{y}}}\over \kidy}}_{消えて欲しい部分} \end{equation} を得る。「消えて欲しい部分」を消すためには、$f\kakko{\ycol{y}}$を「微分すると$Q\kakko{x_0,\ycol{y}}$になる関数」にすればよい。そのような関数の一例として$f\kakko{\ycol{y}}=\int_{y_0}^{\ycol{y}} \coldt Q\kakko{x_0,\tcol{t}}$を選べば、 \begin{equation} U\kakko{\xcol{x},\ycol{y}}=\int_{x_0}^{\xcol{x}}\coldt P\kakko{\tcol{t},\ycol{y}} +\int_{y_0}^{\ycol{y}} \coldt Q\kakko{x_0,\tcol{t}}\label{Uintone} \end{equation} となる(間違いであった式との違い---$Q\kakko{\xcol{x},\tcol{t}}$か$Q\kakko{x_0,\tcol{t}}$か---に注意!)。なお、この選び方により$U\kakko{x_0,y_0}=0$としたことになる。もちろん、$U\kakko{x_0,y_0}$が0ではない場合は右辺に$+U\kakko{x_0,y_0}$を付け加えればよいだけのことである。この$U\kakko{\xcol{x},\ycol{y}}$は$\PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=Q\kakko{\xcol{x},\ycol{y}}$を満たす。$\ycol{y}$のみの関数を付け加えたのだから、$\PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}=P\kakko{\xcol{x},\ycol{y}}$の方もそのまま成り立っている。
なお、ここでやった計算で$\xcol{x}$と$\ycol{y}$の役割を逆転させれば、 \begin{equation} U\kakko{\xcol{x},\ycol{y}}=\int_{x_0}^{\xcol{x}}\coldt P\kakko{\tcol{t},y_0} +\int_{y_0}^{\ycol{y}} \coldt Q\kakko{\xcol{x},\tcol{t}}\label{Uinttwo} \end{equation} という式が作られる。これも正しい$U\kakko{\xcol{x},\ycol{y}}$である。微分してみると、$\PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}=Q\kakko{\xcol{x},\ycol{y}}$なのはもちろん、 \begin{equation} \begin{array}{rl} \PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} =&P\kakko{\xcol{x},y_0}+\int_{y_0}^{\ycol{y}}\coldt \PDC{Q\kakko{\xcol{x},\tcol{t}}}{\xcol{x}}{\tcol{t}}~~\kokode{積分可能条件}\\[4mm] =&P\kakko{\xcol{x},y_0}+\int_{y_0}^{\ycol{y}}\coldt \PDC{P\kakko{\xcol{x},\tcol{t}}}{\tcol{t}}{\xcol{x}}\\[4mm] =&P\kakko{\xcol{x},y_0}+P\kakko{\xcol{x},\ycol{y}}-P\kakko{\xcol{x},y_0}=P\kakko{\xcol{x},\ycol{y}} \end{array} \end{equation} となって、$U\kakko{\xcol{x},\ycol{y}}$の満たすべき条件を満たしている。
二つの積分が「どの場所の何を積分しているか」を図で表したものが次のグラフである。
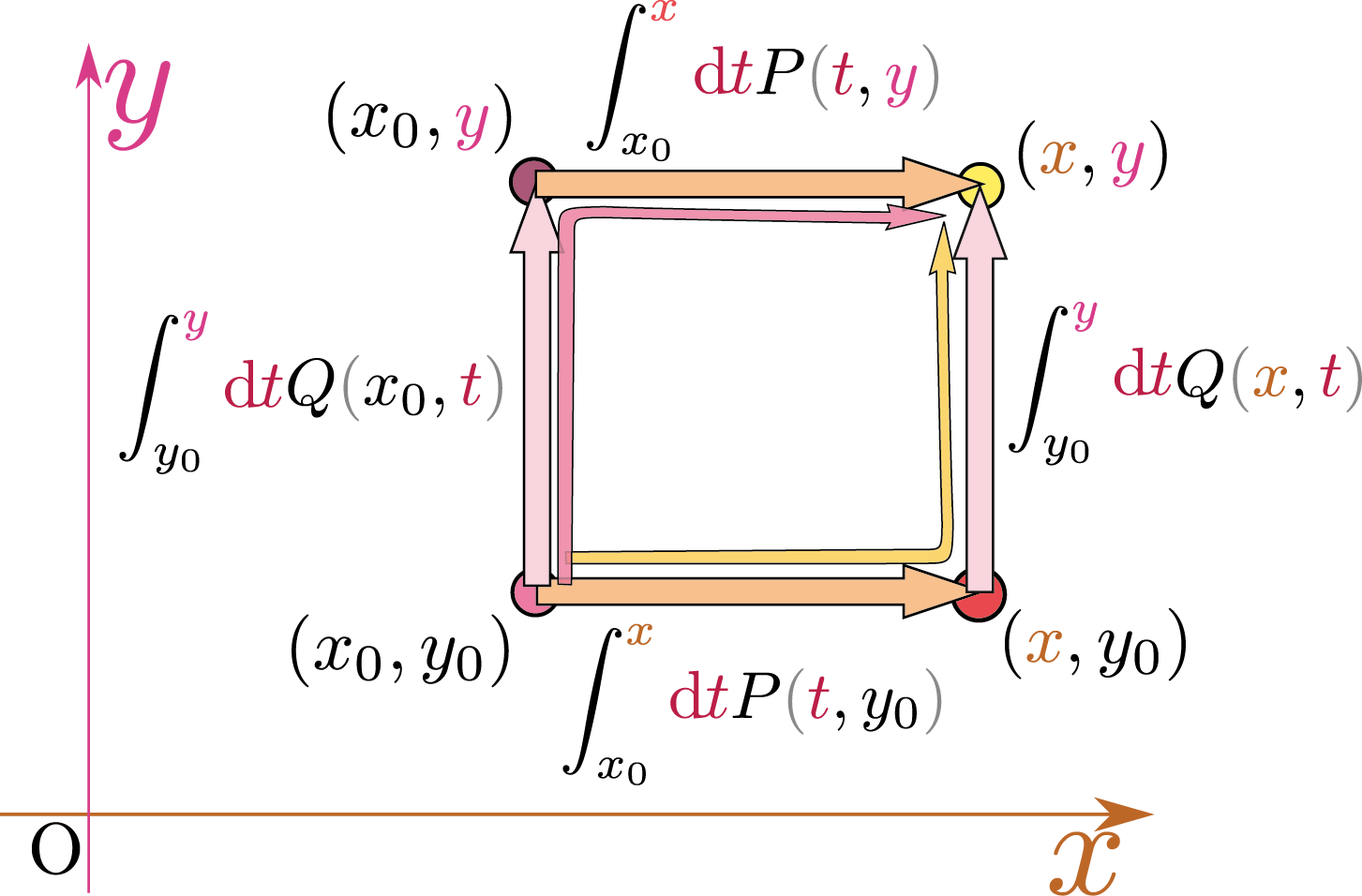
場所$(\xcol{x},\ycol{y})$における$U$を求めるために、場所$(x_0,y_0)$から出発する。 第1の積分ではまず右へ$(\xcol{x},y_0)$まで進んでから上へ$(\xcol{x},\ycol{y})$まで進む。第2の積分でははまず上へ$(x_0,\ycol{y})$まで進んでから右へ$(\xcol{x},\ycol{y})$まで進んでいる。
この二つの積分結果が同じになることが積分可能条件そのものなのだ。
「微分の逆が積分」は何度か述べているが、常微分での$\int_a^b {\diff f\over \diff x}\kakko{\xcol{x}}\coldx=f\kakko{b}-f\kakko{a}$という式を偏微分の時に使おうとすると、
積分ってどの積分?
という問題が生じてくる。積分可能条件が成立してればそこは気にしなくてよくなり、 \begin{equation} U\kakko{\xcol{x},\ycol{y}}= \int_{y_0}^{\ycol{y}} \coldt \PD{U\kakko{x_0,\tcol{t}}}{\tcol{t}} +\int_{x_0}^{\xcol{x}}\coldt \PD{U\kakko{\tcol{t},\ycol{y}}}{\tcol{t}} ~~ または ~~ \int_{x_0}^{\xcol{x}}\coldt \PD{U\kakko{\tcol{t},y_0}}{\tcol{t}} +\int_{y_0}^{\ycol{y}} \coldt \PD{U\kakko{\xcol{x},\tcol{t}}}{\tcol{t}} \end{equation} と書ける(この式は「$U$を微分して積分したら元に戻る」という式になっている)。
より一般的には斜めや曲線の場合も含めて、 \begin{equation} U\kakko{x_1,y_1} = \int_{\vec x_0}^{\vec x_1} \left( \coldx\PD{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}} +\coldy\PD{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}} \right) = \int_{\vec x_0}^{\vec x_1} \xcol{\diff\vec x}\cdot\vec\nabla U\kakko{\xcol{x},\ycol{y}} \end{equation} のように書く(この式では積分変数を$\xcol{x},\ycol{y}$と書くことにしたので、到着点は$\vec x_1=(x_1,y_1)$にしてある)。この式で「経路」を指定してないのは、積分結果が経路によらないことをすでに知っているからである。
以上からわかるように、ある微小量があったとき、それが全微分であるかどうかというのは非常に大事である。ある量が微小量で、かつ全微分である量であったとすれば、そのある量を$\rcol{\diff X}$と書いて、「微分される前の量」である$\rcol{X}$を定義することができる。そうやって定義された$\rcol{X}$は、「変化のさせ方にはよらず、変化後の状態だけで決まる量(状態量)」になり、便利である。
いったん「状態量」であることが証明された量は、「これまでどんな変化をしてきたか」という経歴を一切考慮することなく「今どうなっているか」だけを見て計算し表現することができる。エネルギーなどがこれにあたる。\akantalk{この物体が昨日どこにいたかを知らないとこの物体の位置エネルギーは計算できない}と言われたらどれだけ面倒くさいことになるかと想像してみれば、エネルギーが状態量であることの有難味がわかる。ある微小量が全微分となり、対応する状態量が定義できる(逆にいえば、これを微分すれば最初考えていた「ある微小量」が出て来る)という状況は、たいへん有り難い状況なのだ。
一方、微小量ではあるが全微分ではない量(もちろんこういう量も存在する!)については、対応する状態量を定義できない。
例としては「熱」がある。気体をある状態から微小に違う別の状態に変化させる時に、微小な熱が移動するが、一般的には変化のさせ方で移動する熱量は変わる。だから、「微分すると熱になる量」は特別な場合を除けば定義できない(そういう量は$\diff 'X$のように${}'$をつけて「全微分じゃないよ」と表すこともある)。
積分因子
積分可能条件が満たされてなかったら全微分形ではない。しかし、ここで$P\coldx+Q\coldy=0$の右辺が0なので、両辺にある関数$\lambda\kakko{\xcol{x},\ycol{y}}$を掛けて \begin{equation} \lambda\kakko{\xcol{x},\ycol{y}} P\kakko{\xcol{x},\ycol{y}}\coldx +\lambda\kakko{\xcol{x},\ycol{y}} Q\kakko{\xcol{x},\ycol{y}}\coldy=0 \end{equation} として、 \begin{equation} \begin{array}{rl} \PDC{U\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}&=\lambda\kakko{\xcol{x},\ycol{y}} P\kakko{\xcol{x},\ycol{y}},\\ ~~~ \PDC{U\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}&=\lambda\kakko{\xcol{x},\ycol{y}} Q\kakko{\xcol{x},\ycol{y}} \end{array} \end{equation} を満たすことができれば全微分形ではなかった微分方程式を全微分形に直せた。この掛算した$\lambda\kakko{\xcol{x},\ycol{y}}$のことを「積分因子(integrating factor)」と呼ぶ。積分因子は \begin{equation} \PDC{\left( \lambda\kakko{\xcol{x},\ycol{y}} Q\kakko{\xcol{x},\ycol{y}} \right)}{\xcol{x}}{\ycol{y}}- \PDC{\left( \lambda\kakko{\xcol{x},\ycol{y}} P\kakko{\xcol{x},\ycol{y}} \right)}{\ycol{y}}{\xcol{x}}=0 \end{equation} すなわち \begin{equation} \PDC{\lambda\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} Q\kakko{\xcol{x},\ycol{y}} - \PDC{\lambda\kakko{\xcol{x},\ycol{y}} }{\ycol{y}}{\xcol{x}} P\kakko{\xcol{x},\ycol{y}} = -\lambda\kakko{\xcol{x},\ycol{y}} \PD{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}-\PD{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \end{equation} という方程式を満たせばよい。しかし、この式から$\lambda\kakko{\xcol{x},\ycol{y}}$の形を求めるのは一般には簡単ではない(また、この方程式の解$\lambda\kakko{\xcol{x},\ycol{y}}$は一意ではない)。たまたま、$\lambda$が$\xcol{x}$のみの関数になるような場合はこの式が \begin{equation} \opcol{\diff \kuro{\lambda\kakko{\xcol{x}}} \over \diff x} Q\kakko{\xcol{x},\ycol{y}} = -\lambda\kakko{\xcol{x}} \left( \PD{Q\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}- \PD{P\kakko{\xcol{x},\ycol{y}}}{\ycol{y}} \right)\label{lambdaketteij} \end{equation} という形になるので、少し解きやすくなる。実際に解くときには、いろいろな場合を想定して試行錯誤を行う。
最後に少し物理的な注意。ある微小量が全微分になっているかどうかはとても大事(特に熱力学などで重要)。君たちの知っている例で言うと、運動方程式 $$ m{\mathrm dv\over\mathrm dt}=-{\mathrm d U\over\mathrm dx} $$ は、 $$ m{\mathrm dv}=-{\mathrm d U\over\mathrm dx}\mathrm dt $$ として両辺に$v={\mathrm dx\over\mathrm dt}$を掛けると、 $$ mv{\mathrm dv}=-\mathrm d U $$ となって全微分形になる。積分結果は $$ {1\over2}mv^2 +U = 一定 $$ で、つまりエネルギー保存則。エネルギー保存則は運動方程式を全微分形に直して積分したもの、と考えることができるのである。