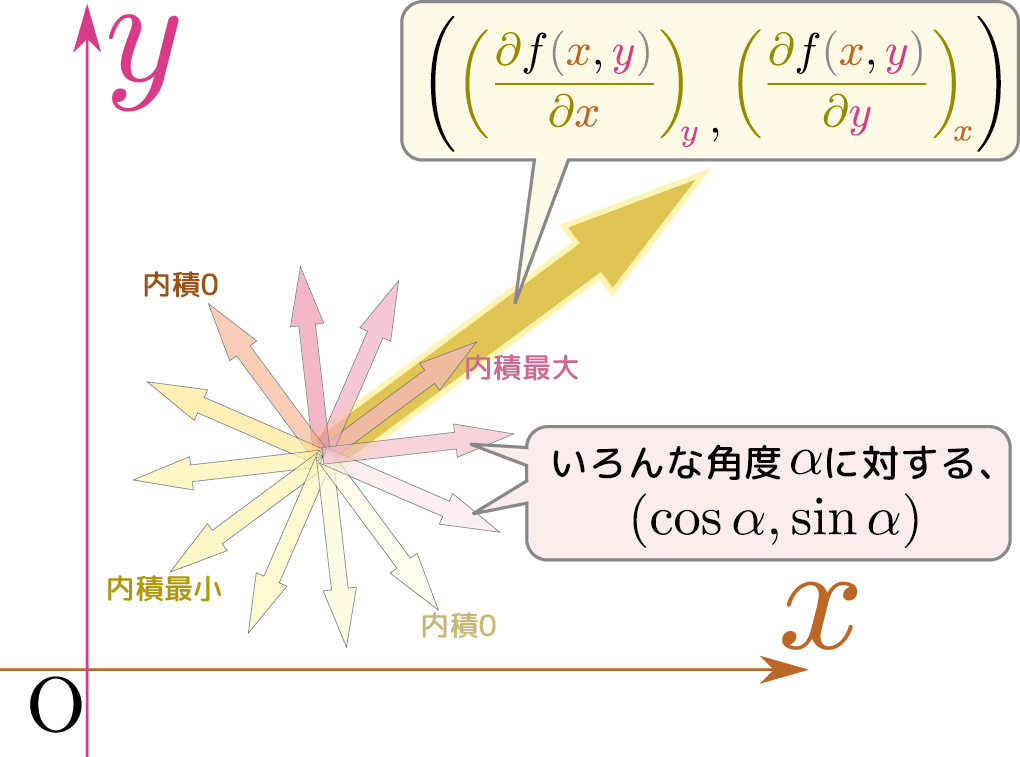
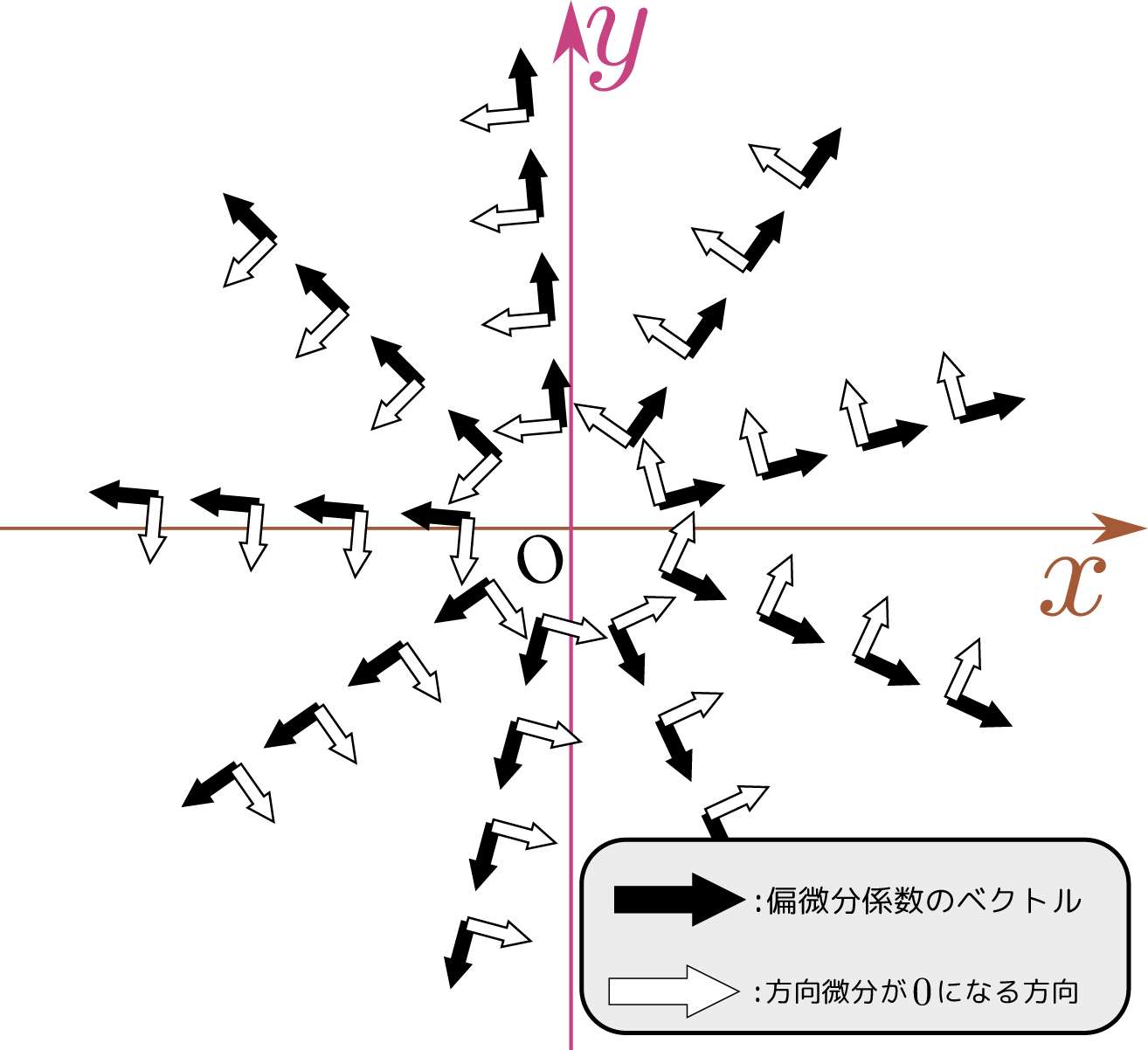
2次元の座標と方向微分
2次元の座標と方向微分
2次元の座標
まず、平面上を考えよう。平面上の位置は、二つの座標によって表現できる。
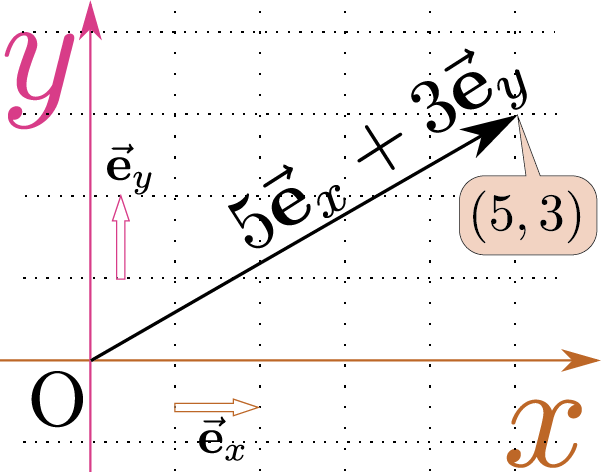
座標とは位置を表現するための数で、よく使われるのは右のように場所を原点からその場所に引っ張った矢印であるベクトル(位置ベクトル)を$\colvecx=\xcol{x}\ve_x+\ycol{y}\ve_y$のように表現したときの$\xcol{x}$と$\ycol{y}$である。図に示したように、$\xcol{x}$軸方向を向いた単位ベクトル(長さが1のベクトルのこと)を$\ve_x$、$\ycol{y}$軸方向を向いた単位ベクトルを$\ve_y$と書いている。
直交座標における「$\xcol{x},\ycol{y},\zcol{z}$方向を向いた単位ベクトル」の表現方法としては、他に、${\mathbf e}_x,{\mathbf e}_y,{\mathbf e}_z$(矢印をつけない)、${\mathbf i},{\mathbf j},{\mathbf k}$や、$\hat {\mathbf x},\hat {\mathbf y},\hat {\mathbf z}$(ハット$\hat {~}$をつける)などがある。記号が違っても中身は変わらない。
位置ベクトルは$\colvecx=\xcol{x}\ve_x+\ycol{y}\ve_y$のように書けるが、成分を並べて$(\xcol{x},\ycol{y})$と書いても位置を表現できる。それぞれの点に応じて一つの数が決まる対応関係がある場合、その対応関係すなわち関数を$f\kakko{\xcol{x},\ycol{y}}$、または$f\kakko{\!\colvecx\!}$と書く$f\kakko{\zcol{\vec x}}$と書いたからといって、関数$f$がベクトルになったわけではない。$f\kakko{\!\colvecx\!}$は「ベクトル$\colvecx$を一個決めると数$f\kakko{\zcol{\vec x}}$が決まる」という関係である。。
2次元の位置を表現するのによく使われるのは直交座標(デカルト座標)で、上で述べた二つの座標$\xcol{x},\ycol{y}$を使って位置を表現する。もう一つよく使われるのが極座標で、これは原点からの距離$\rcol{r}=\sqrt{\xcol{x}^2+\ycol{y}^2}$と、どの方向に原点から離れているかを意味する$\thetacol{\theta}$で位置を表現するその意味からして、$\rcol{r}w=0$(原点)では座標$\thetacol{\theta}$は無意味になることに注意。。
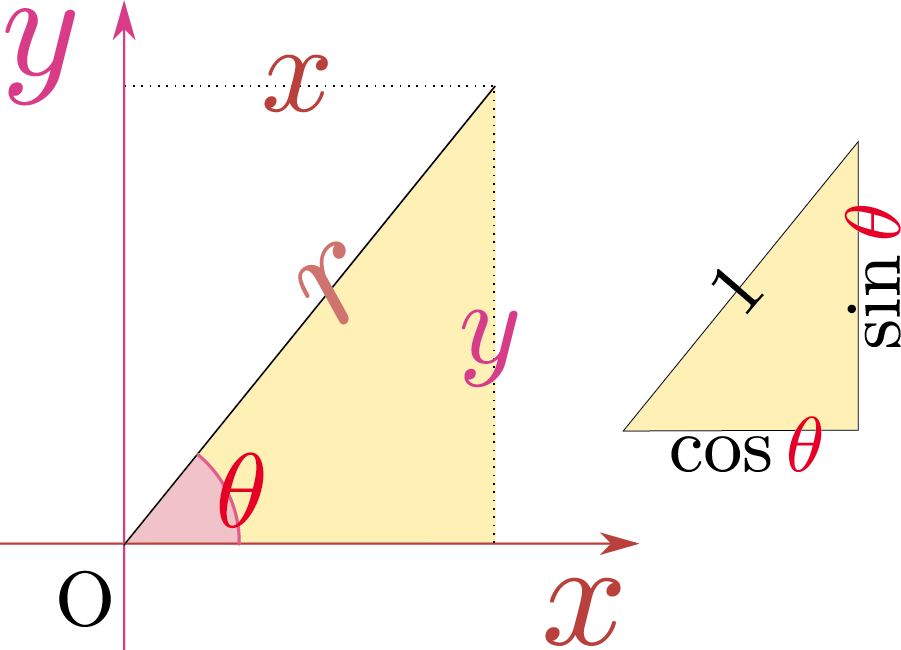
図からわかるように極座標と直交座標には以下のような関係がある。 \begin{equation} \begin{array}{l} \xcol{x}=\rcol{r}\cos \thetacol{\theta},\ycol{y}=\rcol{r}\sin \thetacol{\theta},\\[2mm] \rcol{r}=\sqrt{\xcol{x}^2+\ycol{y}^2},\\ \cos\thetacol{\theta}={\xcol{x}\over \sqrt{\xcol{x}^2+\ycol{y}^2}},\sin\thetacol{\theta}={\ycol{y}\over \sqrt{\xcol{x}^2+\ycol{y}^2}} \end{array} \end{equation}
$\xcol{x},\ycol{y}$はどちらも実数全体$-\infty$から$\infty$が定義域だが、極座標では$0\leq \rcol{r}<\infty$(0以上の数のみ)と$0\leq\thetacol{\theta}<2\pi$となる。$\thetacol{\theta}<2\pi$にしたのは$\thetacol{\theta}=2\pi$にあたる点は$\thetacol{\theta}=0$と同じ点であるからだが、座標に重複を許すならば$-\infty\leq\thetacol{\theta}<\infty$(定義域は実数全体)としてもよい。その場合の$\thetacol{\theta}$という座標は「$2\pi$の整数倍の違いは同じ点を示す」つまり「$\thetacol{\theta}$と$\thetacol{\theta}+2n\pi$($n$は整数)は同一点」という周期性を持つことに注意しなくてはいけない。

直交座標の$\ve_x,\ve_y$同様、極座標でも$\rcol{r}$方向($\rcol{r}$が増加する方向)の単位ベクトル、$\thetacol{\theta}$方向($\thetacol{\theta}$が増加する方向)の単位ベクトルを考えて、これを$\ve_r,\ve_\theta$と書く(${\bf \hat r},{\bf \hat \theta}$と書いている本もある)。図に表したように(そして、その定義から当然そうなるべく)、$\ve_r,\ve_\theta$は場所によって違う方向を向く原点においては、$\ve_r,\ve_\theta$ともに定義できない。この意味で、原点は極座標の「特異点」である。。具体的に言えば$\thetacol{\theta}$によって違う方向を向くので、$\thetacol{\theta}$の関数座標$\thetacol{\theta}$を決めるとベクトルが一つ決まる。数→ベクトルという関数。であると考えれば$\ve_r\kakko{\thetacol{\theta}},\ve_\theta\kakko{\thetacol{\theta}}$と書くべきである(しかししばしば省略する)。
下の図からわかるように、$\ve_r$は$\xcol{x}$成分が$\cos\thetacol{\theta}$、$\ycol{y}$成分が$\sin\thetacol{\theta}$なので、
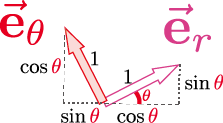
\begin{equation} \ve_r=\cos\thetacol{\theta}\ve_x+\sin\thetacol{\theta}\ve_y \end{equation} となる。同様に$\ve_\theta$は$\xcol{x}$成分が$-\sin\thetacol{\theta}$で$\ycol{y}$成分が$\cos\thetacol{\theta}$となり \begin{equation} \ve_\theta=-\sin \thetacol{\theta}\ve_x+\cos\thetacol{\theta}\ve_y \end{equation} と書ける。この二つのベクトルは直交する($\ve_r\cdot\ve_\theta=0$)。以上がどのような角度$\thetacol{\theta}$のときでも正しいことは、図をたくさん描いて確認して欲しい。
なお、極座標の「$\rcol{r}$方向」と「$\thetacol{\theta}$方向」も直交はしている。「直交座標」という言葉を「座標の方向が直交している座標系」と捉えるならば、極座標も``直交座標''だということになる。本書では「直交座標」は$(\xcol{x},\ycol{y})$を使う座標系(デカルト座標系)の名前として使うことにして、「座標の方向が直交している座標系」は「直交曲線座標」と呼ぶことにする。他の本を読むときには注意すること。
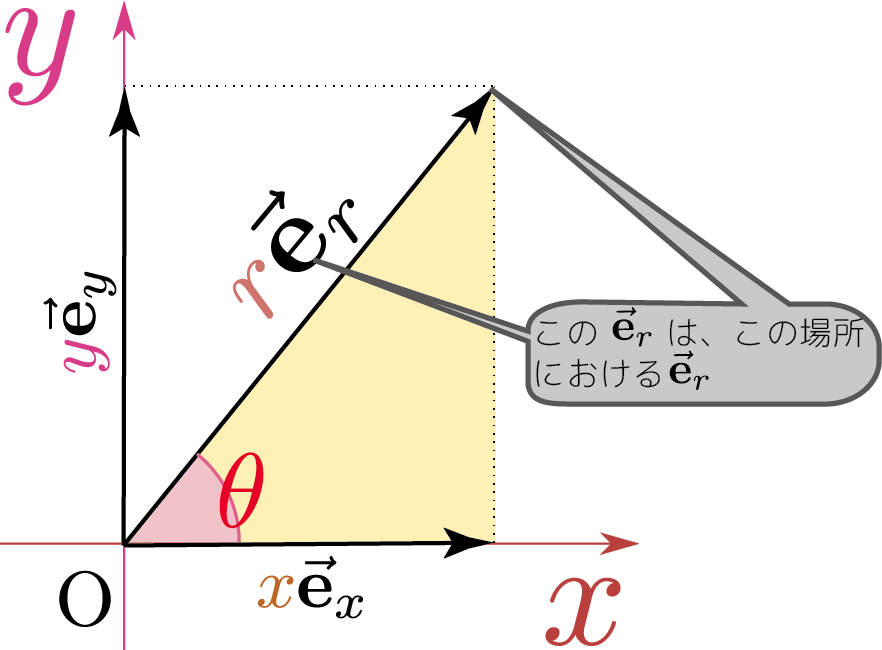
2次元平面上における位置ベクトルは \begin{equation} \overbrace{\colvecx=\xcol{x}\ve_x +\ycol{y}\ve_y}^{直交座標} =\goverbrace{\rcol{r}\ve_r\kakko{\thetacol{\theta}}}^{極座標}\label{ichivec} \end{equation} のように表現される。直交座標では「原点から$\ve_x$の方向に$\xcol{x}$移動し、次に$\ve_y$の方向に$\ycol{y}$移動する」と考えると$\xcol{x}\ve_x +\ycol{y}\ve_y$となる。極座標では$\ve_r\kakko{\thetacol{\theta}}$の方向に$\rcol{r}$だけ移動する。
極座標の位置ベクトルは$\colvecx=\rcol{r}\ve_r\kakko{\thetacol{\theta}}$となり$\ve_\theta$は出てこない。この式はしばしば省略されて$\colvecx=\rcol{r}\ve_r$と書かれる本書でも多くの場面で省略記法の方を使う。が、$\ve_r\kakko{\thetacol{\theta}}$は(たとえ省略して$\ve_r$と書かれていようと)$\thetacol{\theta}$に依存しているのだから、$\colvecx$が$\thetacol{\theta}$に依存していないわけではない。
直交座標と極座標の二つの表現が等しいことは、$\ve_r=\cos \thetacol{\theta}\ve_x+\sin\thetacol{\theta}\ve_y$を代入して \begin{equation} \rcol{r}\overbrace{\left(\cos \thetacol{\theta}\ve_x+\sin\thetacol{\theta}\ve_y\right)}^{\ve_r} =\underbrace{\rcol{r}\cos\thetacol{\theta}}_{\xcol{x}}\ve_x+\underbrace{\rcol{r}\sin\thetacol{\theta}}_{\ycol{y}}\ve_y \end{equation} のように計算して確認することもできる。
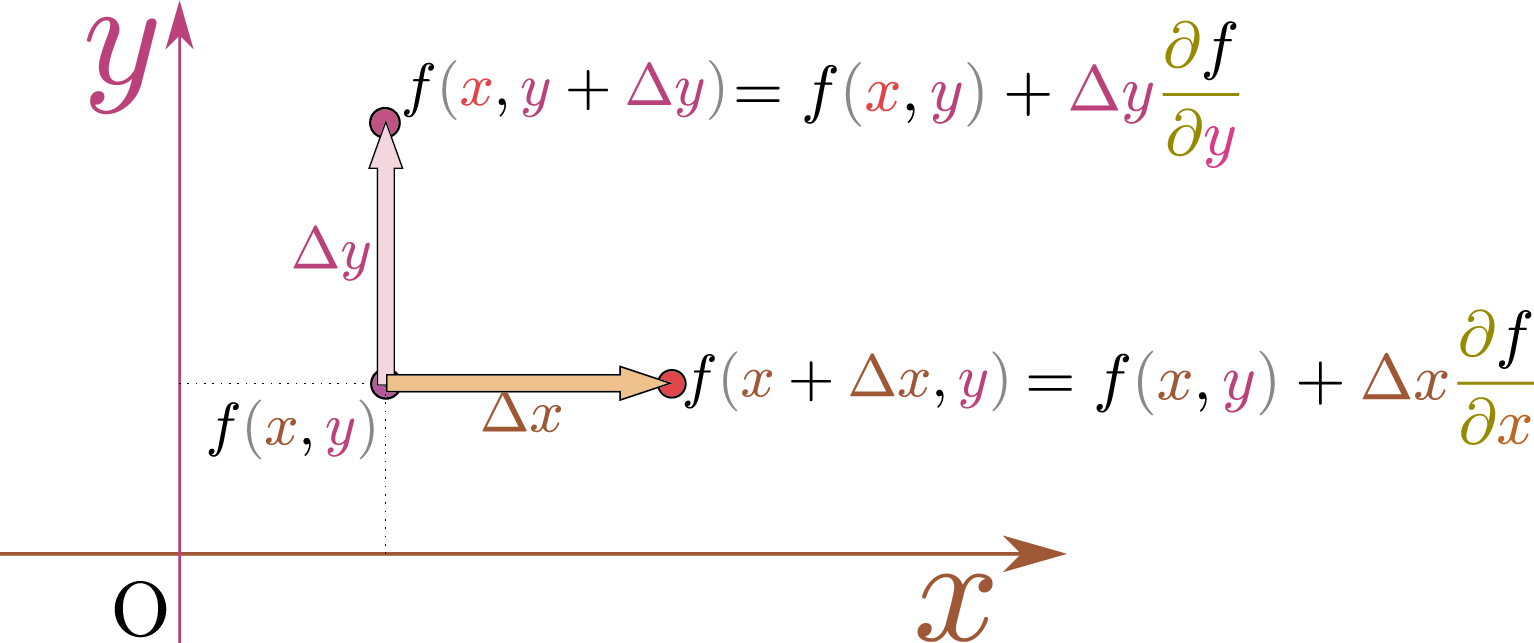
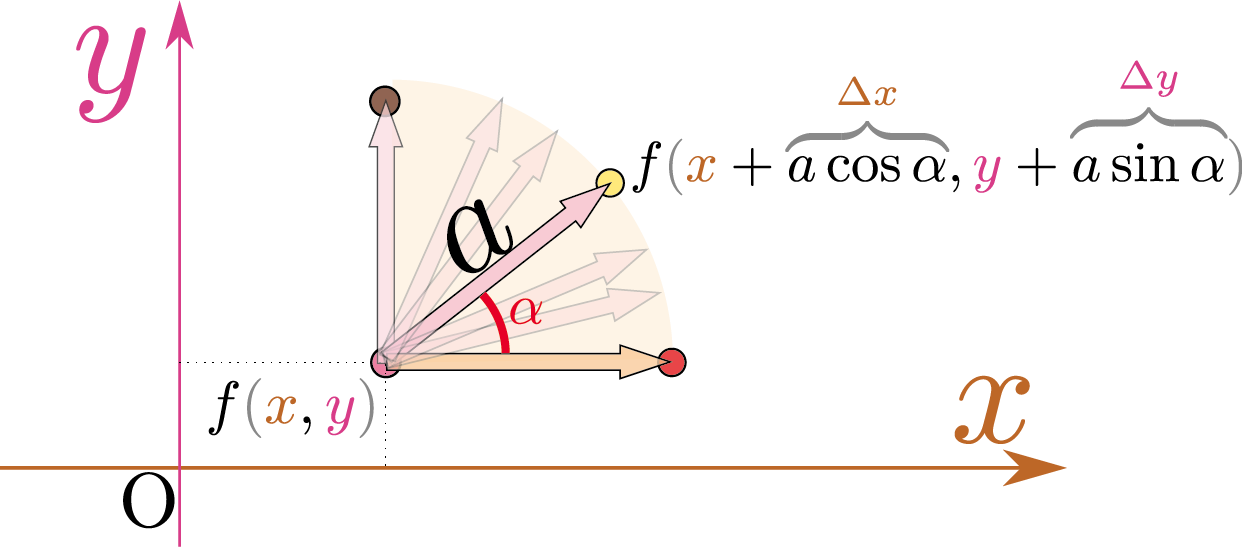
 ←この交通標識は「勾配0.1」の印。
←この交通標識は「勾配0.1」の印。