2次元の座標と方向微分

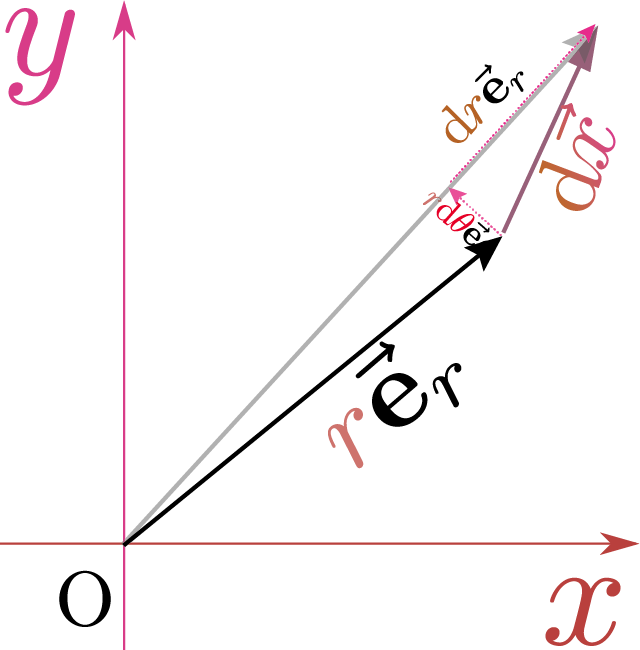
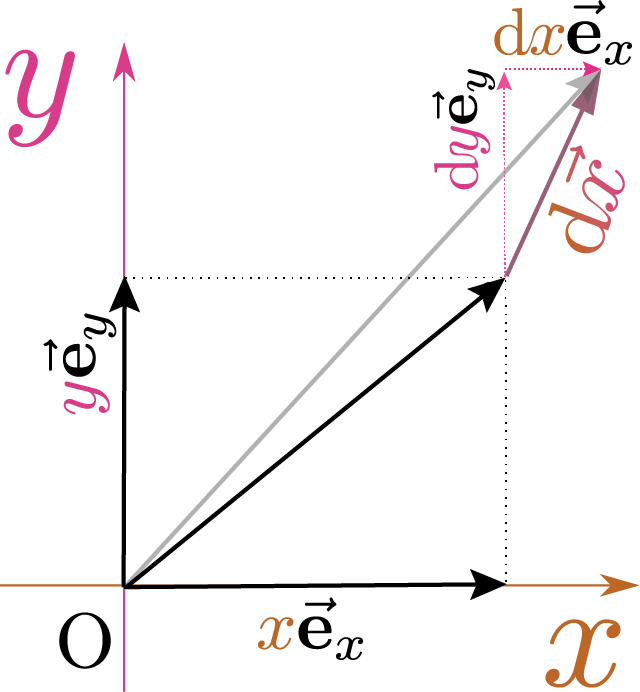$\def\coldr{\rcol{\mathrm dr}}\def\coldvecx{\xcol{\mathrm d\vec x}}\def\intdx{\opcol{\int \mathrm dx}}\def\E{\mathrm e}\def\I{\mathrm i}\definecolor{opcol}{RGB}{149,139,0}\definecolor{hai}{RGB}{137,137,137}\definecolor{tcol}{RGB}{166,54,109}\definecolor{kuro}{RGB}{0,0,0}\definecolor{xcol}{RGB}{169,103,49}\def\opcol#1{{\color{opcol}#1}}\def\ddx{\opcol{{\mathrm d\over \mathrm dx}}}\def\ddt{\opcol{{\mathrm d\over \mathrm dt}}}\def\xcol#1{{\color{xcol}#1}}\definecolor{ycol}{RGB}{217,61,137}\def\ycol#1{{\color{ycol}#1}}\def\haiiro#1{{\color{hai}#1}}\def\kuro#1{{\color{kuro}#1}}\def\kakko#1{\haiiro{\left(\kuro{#1}\right)}}\def\coldx{{\color{xcol}\mathrm dx}}\def\Odr{{\cal O}}\definecolor{ncol}{RGB}{217,51,43}\def\ncol#1{{\color{ncol}#1}}\definecolor{zcol}{RGB}{196,77,132}\def\zcol#1{{\color{zcol}#1}}\definecolor{thetacol}{RGB}{230,0,39}\def\thetacol#1{{\color{thetacol}#1}}\def\diff{\mathrm d}\def\kidb{\opcol{\mathrm db}}\def\kidx{\opcol{\mathrm dx}}\def\coldy{\ycol{\mathrm dy}}\def\coldtheta{\thetacol{\mathrm d\theta}}\def\ddtheta{\opcol{{\mathrm d\over\mathrm d\theta}}}\def\tcol#1{{\color{tcol}#1}}\def\coldt{\tcol{\mathrm dt}}\def\kidtheta{\opcol{\mathrm d\theta}}\def\dtwodx{\opcol{\diff^2\over\diff x^2}}\def\kokode#1{{↓#1}}\def\goverbrace{\overbrace}\def\coldz{\zcol{\mathrm dz}}\def\kidt{\opcol{\mathrm dt}}\definecolor{rcol}{RGB}{206,114,108}\def\rcol#1{{\color{rcol}#1}}\def\coldtwox{\xcol{\mathrm d^2x}}\def\PDC#1#2#3{{\opcol{\left(\opcol{{\partial \kuro{#1}\over \partial #2}}\right)}}_{#3}}\def\PDIC#1#2#3{{\opcol{\left(\opcol{\partial \over \partial #2}\kuro{#1}\right)}}_{#3}}\def\PD#1#2{{\opcol{\partial \kuro{#1}\over \partial #2}}}\def\PPDC#1#2#3{{\opcol{\left(\opcol{\partial^2 \kuro{#1}\over \partial #2^2}\right)}}_{#3}}\def\PPDD#1#2#3{{\opcol{{\partial^2 \kuro{#1}\over \partial #2\partial #3}}}}\def\PPD#1#2{{\opcol{{\partial^2 \kuro{#1}\over \partial #2^2}}}}\def\kidy{\opcol{\diff y}}\def\ve{\vec{\mathbf e}}\def\colvecx{\xcol{\vec x}}\definecolor{usuopcolor}{RGB}{237,234,203}\def\usuopcol#1{\color{usuopcolor}#1}\def\vgrad#1{{\usuopcol{\overrightarrow{\opcol{\rm grad}~\kuro{#1}}}}}$

2次元の座標と方向微分（続き）

　 前回は2次元の方向微分が $$ \vgrad{f\kakko{\xcol{x},\ycol{y}}}=\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\ve_x + \PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\ve_y $$ という「勾配（grad）」と呼ばれるベクトルと、考えている方向を向いた単位ベクトルの内積で表現できる、という話までした。

　gradと単位ベクトルの内積を作ると、 $$ \begin{array}{rl} \ve_x\cdot\vgrad{f\kakko{\xcol{x},\ycol{y}}}=&\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\\ \ve_y\cdot\vgrad{f\kakko{\xcol{x},\ycol{y}}}=&\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\\ \ve_r\cdot\vgrad{f\kakko{\xcol{x},\ycol{y}}}=&\PDC{f\kakko{\xcol{x},\ycol{y}}}{\rcol{r}}{\thetacol{\theta}}\\ \end{array} $$ のようにその方向の微分が出て来る、というところまで先週説明した。では、 $$ \ve_\theta\cdot\vgrad{f\kakko{\xcol{x},\ycol{y}}}=\PDC{f\kakko{\xcol{x},\ycol{y}}}{\thetacol{\theta}}{\rcol{r}} $$ となるのかな？？---というところで先週は終わった。さて実際計算してみると、 $$ \begin{array}{rl} \ve_\theta\cdot\vgrad{f\kakko{\xcol{x},\ycol{y}}}=\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\underbrace{\ve_\theta\cdot\ve_x}_{-\sin\thetacol{\theta}} + \PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}\underbrace{\ve_\theta\cdot\ve_y}_{\cos\thetacol{\theta}} \end{array} $$ となる。

　一方、$\thetacol{\theta}$微分がどうなるかを確認しよう。そのため、$\xcol{x},\ycol{y}$による微分と$\rcol{r},\thetacol{\theta}$による微分の間の関係式が欲しい。そこで、直交座標で考えた関数$f\kakko{\xcol{x},\ycol{y}}$を、極座標で書き直すところから始めよう。直交座標の関数を極座標での関数に書き直した結果を関数$g\kakko{\rcol{r},\thetacol{\theta}}$として、 $$ f\kakko{\xcol{x},\ycol{y}}\biggr|_{\xcol{x}=\rcol{r}\cos \thetacol{\theta},\atop\ycol{y}=\rcol{r}\sin \thetacol{\theta}\phantom{,}}=g\kakko{\rcol{r},\thetacol{\theta}} $$ と書こう。一例を示すなら、$f\kakko{\xcol{x},\ycol{y}}=\xcol{x}\ycol{y}$とすれば、$g\kakko{\rcol{r},\thetacol{\theta}}=\rcol{r}^2\cos\thetacol{\theta}\sin\thetacol{\theta}$である。これを、 \begin{equation} f\kakko{ {x}\kakko{\rcol{r},\thetacol{\theta}},{y}\kakko{\rcol{r},\thetacol{\theta}}} =g\kakko{\rcol{r},\thetacol{\theta}}\label{fxyrtheta} \end{equation} と表現してもよい。この書き方では、$\rcol{r},\thetacol{\theta}$を決めると${x}\kakko{\rcol{r},\thetacol{\theta}}$と${y}\kakko{\rcol{r},\thetacol{\theta}}$が決まり、それによって$f$の値が決まる。これを（$\thetacol{\theta}$を一定として）$\rcol{r}$で微分する。その意味するところは、 \begin{equation} \PDC{f\kakko{ x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}} }}{\rcol{r}} {\thetacol{\theta}} =\lim_{\rcol{\Delta r}\to0} { f\!\haiiro{(} x\!\haiiro{(\rcol{r}\goverbrace{+\rcol{\Delta r}}^{{変化}},\thetacol{\theta})},y\!\haiiro{(\rcol{r}\goverbrace{+\rcol{\Delta r}}^{{変化}},\thetacol{\theta})} \haiiro{)} -f\kakko{ x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}} } \over \rcol{\Delta r} }\label{delfdelr} \end{equation} である。

　$\PD{}{\rcol{r}}$という微分演算子は$\rcol{r}$を$\rcol{\Delta r}$だけ変化させた時の変化量を$\rcol{\Delta r}$で割る（そして$\rcol{\Delta r}\to0$の極限を取る）という演算であるということを思い起こし、ここでは$\rcol{r}$が$\rcol{\Delta r}$だけ変化が起こる場所が二箇所あることに注意しよう。ここで、 \begin{equation} x\kakko{\rcol{r}+\rcol{\Delta r},\thetacol{\theta}}=x\kakko{\rcol{r},\thetacol{\theta}} +\PD{x\kakko{\rcol{r},\thetacol{\theta}}}{r}\rcol{\Delta r},~~ y\kakko{\rcol{r}+\rcol{\Delta r},\thetacol{\theta}}=y\kakko{\rcol{r},\thetacol{\theta}} +\PD{y\kakko{\rcol{r},\thetacol{\theta}}}{r}\rcol{\Delta r}\label{eqdeltar} \end{equation} を使い\式{delfdelr}の右辺分子を$f\kakko{x\kakko{\rcol{r},\thetacol{\theta}}+\PD{x\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}\rcol{\Delta r},y\kakko{\rcol{r},\thetacol{\theta}}+\PD{y\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}\rcol{\Delta r}}-f\kakko{x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}}}$と書く。第1項を$f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}+\ycol{\Delta y}}=f\kakko{\xcol{x},\ycol{y}}+\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}\xcol{\Delta x}+\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\ycol{\Delta y}$}のように$\xcol{\Delta x}\ycol{\Delta y}$の1次まで展開すれば \begin{equation} f\kakko{ x\kakko{\rcol{r}{+\rcol{\Delta r}},\thetacol{\theta}},y\kakko{\rcol{r}{+\rcol{\Delta r}},\thetacol{\theta}}} = f\kakko{ x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}} } +\underbrace{\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}\goverbrace{\PD{x\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}\rcol{\Delta r}}^{\xcol{\Delta x}}}_{xの変化による部分} +\underbrace{\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\goverbrace{\PD{y\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}\rcol{\Delta r}}^{\ycol{\Delta y}}}_{yの変化による部分} \end{equation} のようになる（$\Odr\kakko{(\rcol{\Delta r})^2}$は省略）から、引算を実行した結果を$\rcol{\Delta r}$で割ることにより、 \begin{equation} \PD{f\kakko{x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}}}}{\rcol{r}} =\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}\PD{x\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}} +\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\PD{y\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}\label{delfdelrkekka} \end{equation} となる。これが偏微分における連鎖律である。

　常微分での連鎖律 \begin{equation} \ddx f\kakko{g\kakko{\xcol{x}}}={\mathrm df\over \mathrm dg}\kakko{g\kakko{\xcol{x}}}{\mathrm dg\over\dx}\kakko{\xcol{x}} \end{equation} と比較すると項が二つ出てきた点が違うが、これは当然である。上の式では「$f\kakko{x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}}}$という式を$\rcol{r}$で微分する」という操作を行ったが、微分される相手である$f\kakko{x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}}}$の中には$\rcol{r}$が2箇所入っている。「だから微分の結果も二つの項になったのだ」新しい「計算ルール」を知ったとき、「このルールはどこから来たか」を理解するよう努めよう。闇雲にルールとして覚えるより効率がいい。と考えると、やっている計算の本質は常微分でも偏微分でも同じであることがわかる。

　同様に、${\thetacol{\theta}}$の方の微分は以下の通り。 \begin{equation} \PD{f\kakko{x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}}}}{{\thetacol{\theta}}} =\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}\PD{x\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}} +\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}\PD{y\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}}\label{delfdelthetakekka} \end{equation} となるので、$\thetacol{\theta}$微分は \begin{equation} \begin{array}{rl} \PD{f\bigl(x\kakko{\rcol{r},\thetacol{\theta}},y\kakko{\rcol{r},\thetacol{\theta}} \bigr)}{{\thetacol{\theta}}} =&\goverbrace{-\rcol{r}\sin {\thetacol{\theta}}}^{\PD{x\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}}} ~\PD{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}} +\goverbrace{\rcol{r}\cos {\thetacol{\theta}}}^{\PD{y\kakko{\rcol{r},\thetacol{\theta}}}{{\thetacol{\theta}}}}~\PD{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}} \end{array}\label{delthetatheta} \end{equation} となり、$\thetacol{\theta}$方向の方向微分とは、$\rcol{r}$倍違う$\left(\ve_\theta\cdot(\vgrad{f\kakko{x\kakko{\rcol{r},\thetacol{\theta}}}})={1\over \rcol{r}}\PD{f\kakko{x\kakko{\rcol{r},\thetacol{\theta}}}}{{\thetacol{\theta}}}\right)$。

　$\thetacol{\theta}$微分だけ一致しないのは、$\xcol{x},\ycol{y},\rcol{r}$と$\thetacol{\theta}$にある「違い」があるからである。何が違いだろう？---単位を考えてみるとどうかな？

　$\xcol{x},\ycol{y},\rcol{r}$はメートルで測るけど、$\thetacol{\theta}$はラジアンで測ります。

　そう、つまり$\xcol{x},\ycol{y},\rcol{r}$は「長さ」という意味を持つ量だけど、$\thetacol{\theta}$は、「角度」であって長さじゃない。そこが大きな違いで、方向微分を考えるときは

\begin{equation} \lim_{a\to0}{ f\kakko{\xcol{x}+ \goverbrace{\tcol{a}\cos\alpha}^{\xcol{\Delta x}},\ycol{y}+\goverbrace{\tcol{a}\sin\alpha}^{\ycol{\Delta y}}}-f\kakko{\xcol{x},\ycol{y}}\over \tcol{a} } =\PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \cos\alpha +\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \sin\alpha\label{houkoubibun} \end{equation}

のように、差（分子）を長さ$a$（分母）で割った。$\xcol{x},\ycol{y},\rcol{r}$方向の微分のときは長さ$a$がそれぞれ、$\xcol{\Delta x},\ycol{\Delta y}\rcol{\Delta r}$になったけど、$\thetacol{\theta}$方向だけは、この距離が$\thetacol{\Delta \theta}$ではなく、$\rcol{r}\thetacol{\Delta \theta}$になる。分母に$\rcol{r}$があるぶん、差が出るというわけです。

　以上をまとめると、$\ve_r\cdot\vgrad{f}=\PD{f}{\rcol{r}},\ve_\theta\cdot\vgrad{f}={1\over \rcol{r}}\PD{f}{\thetacol{\theta}}$となるので、

---

2次元極座標のナブラ

\begin{equation} \opcol{\vec \nabla}=\ve_r\PD{}{\rcol{r}}+{1\over \rcol{r}}\ve_\theta\PD{}{\thetacol{\theta}}\label{kyunabla} \end{equation} と定義されることになる。

---

2変数の一般的変数変換

　ここで、一般的な2変数の関数の変数変換をまとめておく。

　$(\xcol{x},\ycol{y})$から$(\rcol{X},\thetacol{Y})$へと変数を変える。もちろん、$\rcol{X},\thetacol{Y}$は両方とも$\xcol{x},\ycol{y}$の関数で、$\rcol{X}=X\kakko{\xcol{x},\ycol{y}},\thetacol{Y}=Y\kakko{\xcol{x},\ycol{y}}$となっている。$f\kakko{\xcol{x},\ycol{y}}$を、$\rcol{X},\thetacol{Y}$の関数として表すと$g\kakko{\rcol{X},\thetacol{Y}}$となるとする。具体的に \begin{equation} f\kakko{\xcol{x},\ycol{y}}=g\left({X}\kakko{\xcol{x},\ycol{y}},{Y}\kakko{\xcol{x},\ycol{y}}\right) \end{equation} であるとする。この式の両辺の$\xcol{x}$による偏微分を定義どおりに計算すると、 \begin{equation} \begin{array}{rl} &\lim_{\xcol{\Delta x}\to0} { f\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}}-f\kakko{\xcol{x},\ycol{y}} \over \xcol{\Delta x}}\\[3mm] =&\lim_{\xcol{\Delta x}\to0}{ g\left({X}(\xcol{x}+\xcol{\Delta x},\ycol{y}),{Y}\kakko{\xcol{x}+\xcol{\Delta x},\ycol{y}}\right) -g\left({X}(\xcol{x},\ycol{y}),{Y}\kakko{\xcol{x},\ycol{y}}\right) \over \xcol{\Delta x} } \end{array} \end{equation} となり、前節同様の計算を行い、以下を得る。 \begin{equation} \PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}= \PDC{X\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \PDC{g\kakko{\zcol{X},\rcol{Y}}}{\zcol{X}}{\rcol{Y}} + \PDC{Y\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}}\label{ippanhenbibunhenkan} \PDC{g\kakko{\zcol{X},\rcol{Y}}}{\rcol{Y}}{ \zcol{X}} \end{equation} \begin{equation} \PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}}= \PDC{X\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \PDC{g\kakko{{\zcol{X}},{\rcol{Y}}}}{\zcol{X}}{\rcol{Y}} + \PDC{Y\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \PDC{g\kakko{{\zcol{X}},{\rcol{Y}}}}{\rcol{Y}}{\zcol{X}}\label{ippanhenbibunhenkantwo} \end{equation}

　任意の関数に対して上の式が成り立つから、「後ろにある関数$f\kakko{\xcol{x},\ycol{y}}$または$g\kakko{\zcol{X},\rcol{Y}}$を省略した形」で書いて 　\begin{equation} \begin{array}{rl} \PD{}{\xcol{x}}=& \PDC{X\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \PD{}{\zcol{X}}+ \PDC{Y\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \PD{}{\rcol{Y}}\\[3mm] \PD{}{\ycol{y}}=& \PDC{X\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \PD{}{\zcol{X}}+ \PDC{Y\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \PD{}{\rcol{Y}} \end{array}\label{xyXYkankei} \end{equation} のような微分演算子相互の関係があると考えてもよい。

　常微分の時の$\ddx f\kakko{g\kakko{\xcol{x}}}={\mathrm df\over \mathrm dg}{\mathrm dg\over \mathrm dx}$という連鎖律に対しては$\mathrm dg$が約分されたと思えという簡単な考えができたが、偏微分の場合に$\kuro{\PD{g}{\zcol{X}}\PD{X}{\xcol{x}}}$で$\opcol{\partial \zcol{X}}$を約分して$\PD{g}{\xcol{x}}$は「大間違い」なので気をつけよう。

　この微分の変換から、直交座標と極座標の$\vec\nabla$の関係を直接出すことももちろんできる。 　\begin{equation} \begin{array}{rl} \PD{}{\rcol{r}}= \underbrace{\PDC{x\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}{\thetacol{\theta}}}_{\cos\thetacol{\theta}} \PD{}{\xcol{x}}+ \underbrace{\PDC{y\kakko{\rcol{r},\thetacol{\theta}}}{\rcol{r}}{\thetacol{\theta}}}_{\sin\thetacol{\theta}} \PD{}{\ycol{y}},~~~ \PD{}{\thetacol{\theta}}=& \underbrace{\PDC{x\kakko{\rcol{r},\thetacol{\theta}}}{\thetacol{\theta}}{\rcol{r}}}_{-\rcol{r}\sin\thetacol{\theta}} \PD{}{\xcol{x}}+ \underbrace{\PDC{y\kakko{\rcol{r},\thetacol{\theta}}}{\thetacol{\theta}}{\rcol{r}}}_{\rcol{r}\cos\thetacol{\theta}} \PD{}{\ycol{y}}\\ \end{array}\label{rthetaxykankei} \end{equation} となりこれから、 \begin{equation} \begin{array}{rl} \opcol{\vec \nabla} =&\ve_r\left(\cos\thetacol{\theta}\PD{}{\xcol{x}}+\sin\thetacol{\theta}\PD{}{\ycol{y}}\right) +{1\over \rcol{r}}\ve_\theta\left(-\rcol{r}\sin \thetacol{\theta}\PD{}{\xcol{x}}+\rcol{r}\cos \thetacol{\theta}\PD{}{\ycol{y}}\right)\\[3mm] =&\underbrace{\left(\ve_r\cos\thetacol{\theta}+\ve_\theta\sin \thetacol{\theta}\right)}_{\ve_x}\PD{}{\xcol{x}} +\underbrace{\left(\ve_r\sin\thetacol{\theta}-\ve_\theta\cos \thetacol{\theta}\right)}_{\ve_y}\PD{}{\ycol{y}} \end{array} \end{equation} となって、確かに二つの表現は同じである。

　ここでちょっと練習問題。 \begin{equation} \begin{array}{l} x=\sqrt{A}\cos\theta,y=\sqrt{A}\sin\theta,\\ A=x^2+y^2 \end{array} \end{equation} のような$(A,\theta)$という座標系の場合で、${\partial f\over\partial A}$と${\partial f\over\partial \theta}$を計算せよ。

　答えは \begin{equation} \PDC{f\kakko{\rcol{A},\thetacol{\theta}}}{\rcol{A}}{\thetacol{\theta}}= \PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \underbrace{\PDC{x\kakko{\rcol{A},\thetacol{\theta}}}{\rcol{A}}{\thetacol{\theta}}}_{{1\over2\sqrt{A}}\cos\thetacol{\theta}} +\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \underbrace{\PDC{y\kakko{\rcol{A},\thetacol{\theta}}}{\rcol{A}}{\thetacol{\theta}}}_{{1\over2\sqrt{A}}\cos\thetacol{\theta}} \end{equation} \begin{equation} \PDC{f\kakko{\rcol{A},\thetacol{\theta}}}{\thetacol{\theta}}{\rcol{A}}= \PDC{f\kakko{\xcol{x},\ycol{y}}}{\xcol{x}}{\ycol{y}} \underbrace{\PDC{x\kakko{\rcol{A},\thetacol{\theta}}}{\thetacol{\theta}}{\rcol{A}}}_{-\sqrt{A}\sin\thetacol{\theta}} +\PDC{f\kakko{\xcol{x},\ycol{y}}}{\ycol{y}}{\xcol{x}} \underbrace{\PDC{y\kakko{\rcol{A},\thetacol{\theta}}}{\thetacol{\theta}}{\rcol{A}}}_{{\sqrt{A}}\sin\thetacol{\theta}} \end{equation} となる。

　$\PD{f}{r}$と$\PD{f}{A}$は$2\sqrt{A}$倍違うが、それはちょうど$\PD{A}{r}=2r$の分である（$\PD{f}{A}\PD{A}{r}=\PD{f}{r}$に注意）。

直交座標と極座標の微小変位

　位置ベクトル$\overbrace{\colvecx=\xcol{x}\ve_x +\ycol{y}\ve_y}^{直交座標} =\overbrace{\rcol{r}\ve_r}^{極座標}$の全微分を計算すると「微小変位ベクトル」が計算できる。

　直交座標の方は変化するのは（変数なのは）$\xcol{x},\ycol{y}$だから、 \begin{equation} \coldvecx = \coldx \ve_x +\coldy \ve_y\label{dvecxxy} \end{equation} となる。直交座標の場合、$\ve_x,\ve_y$は場所によらない（よって$\diff \ve_x=0,\diff\ve_y=0$）ので、比較的単純に微小変化を計算できる。

　一方、$\ve_r$と$\ve_\theta$は場所によって変化する（厳密には$\ve_r\kakko{\thetacol{\theta}},\ve_\theta\kakko{\thetacol{\theta}}$と書くべき）ため、極座標の方は注意が必要である。$\ve_r$の全微分は \begin{equation} \diff \ve_r = \coldtheta \ve_\theta\label{nijigeneretheta} \end{equation} となる。

　上の図に書いたように、$\thetacol{\theta}$が$\coldtheta$だけ違う場所の$\ve_r$は、角度$\coldtheta$だけ違う方向を向いている。$\ve_r$は長さ1である。長さが1で角度が$\coldtheta$違う二つの差を取ると、結果は長さ$\coldtheta$のベクトルとなり、その方向は$\ve_\theta$と同じ方向を向いている（図にあるように、二つの$\ve_r$は半径１で中心角$\coldtheta$の扇形を作り、弧の長さが$\coldtheta$）と考えると$\diff \ve_r = \coldtheta \ve_\theta$}がわかる。

　よって、極座標での微小変位のベクトルは \begin{equation} \coldvecx = \coldr\ve_r+\rcol{r}\coldtheta\ve_\theta \end{equation} のように表せる$\rcol{r}\ve_\theta$という「数とベクトルの積」に対してもライプニッツ則を使って計算してよい。つまり、$\diff \left(\rcol{r}\ve_r\right)=\coldr\ve_\theta+\rcol{r}\diff\ve_\theta$}と考える。。

　これは、次のように図で考えても理解できるだろう。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。