三角関数の話の残り

　先週最後にsinθのθが小さい場合を計算してみようってのをやってその答えだけを板書して「種明かしは来週」で終わったのでここで種明かし。

sin 0.1	≒0.099833416646828
sin 0.01	≒0.009999833334167
sin 0.001	≒0.000999999833333
sin 0.0001	≒0.000099999999833

のようになり、だいたい$\sin\theta \simeq \theta$であることがわかる。

　こうなる理由は、前回やった$\sin\theta$の定義の図に角度$\theta$を描き込んでみるとわかる。

　この角度θをどんどん小さくしていけば、θとsinθは区別がつかなくなる、ということになる。

　ちなみにcosで同じことをやると、

cos 0.1	≒0.995004165278026
cos 0.01	≒0.999950000416665
cos 0.001	≒0.999999500000042
cos 0.0001	≒0.999999995

となる。今度は、$\cos\theta\simeq1-{\theta^2\over2}$が読み取れる。

　こちらは、$\sin^2\theta+\cos^2\theta=1$を思い出せばよい。 $$ \begin{array}{rl} \overbrace{\theta^2}^{\sin^2\theta}+\overbrace{\left(1-{1\over2}\theta^2\right)^2}^{\cos^2\theta}=&\theta^2+1-\theta^2+\underbrace{{\theta^4\over4}}_{無視}\\ =&1 \end{array} $$ となることから、$\cos\theta$がこうであればうまくいくことがわかる。

　なお、${\theta^2\over4}$が無視できるのは、今考えている$\theta$が$0.01={1\over 100}$ぐらいの値だと思えば、$\theta^2$が1万分の1程度、$\theta^4$が1億分の1程度、と考えれば理解できるだろう。

合成関数

合成関数

　関数は「数→数」の対応関係であるが、この対応関係を二段階にしたもの「数→数→数」を「合成関数」と呼ぶ。

　たとえば、ある部屋をクーラーで冷やしているとしよう。クーラーの電力を変えれば温度が変わる（電力→温度）。そして、温度が変わればその気体中の音速が変わる（温度→音速）。こうすると「電力を変えれば（温度の変化を通じて）音速が変わる」（電力→温度→音速）という関数関係ができることになる。

　こんなふうに日常的な話でも「関連する数の変化を追いかけて合成していく」ということをやっている。これが「合成関数」の気持ち。

　数式の例をあげよう。${y}=1-{x^2}$という${x}\to {y}$という対応関係があり、さらに${z}=\sqrt{{y}}$という${y}\to {z}$の対応関係があれば、この二つをまとめて、${z}=\sqrt{1-{x}^2}$という${x}\to{z}$という「合成関数」を作ることができる。

　二つの関数を${y}=f({x})$（yがxの関数である）および${z}=g({y})$（zがyの関数である）と書けば、合成関数は${z}=g(f({x}))$のように書ける（この式の意味は「まず$f({x})$を計算して、計算結果を$g({y})$のyに代入すると、zが求められる」ということだ）$g(f({x}))$を$(g\circ f)({x})$と書くこともある。。

図は

$f({x})={x}^3-{x}^2-2{x}+1$

$g({y})=\sin 3{y}$

の場合で、この時、

\begin{equation} {z}=g(f({x}))= \sin \left(3({x}^3-{x}^2-2{x}+1)\right) \end{equation}

ということになるyの変化の激しいところでは合成関数の結果であるzが激しく振動する、という様子が見て取れる。。

　下に、動かせる合成関数の図をつける。

　ここでは、

y=xという関数と

z=yという関数が合成され、

z=(x)という関数になっている。

---

　◆や◆や◆のような形が走り回っているが、これはx,y,zの変化を表したものである。

のように関数が合成されるところを確認しよう（もちろん他にももっといろいろなパターンがあるので、試してみよう）。

逆関数のペア

　これらの関数は互いに逆関数になっているペアがある。それらを確認しよう。

　上の図ではx→y→zという合成関数を考えているが、２個めのy zが１個めのx yの逆関数であるので、x→y→xというつながりで元に戻ってくる。

　よって、正しく逆関数になっていれば、z=xになるはずだ。

　ただし、実際やってみるとわかるように、これらは全てがちゃんとした逆関数にはなっていない。たとえばy=x²という関数はxが正でも負でも結果のyは正になる。そして、x=√|y|)の結果はどちらにしろ正の数になる。よって、x＜0である状況では「xの符号を外す（絶対値を取る）」ということをしてしまって、逆関数にならないじゃあどうなるか、は上で確認すべし！。

　同じような状況が他の場合でも起こり、上の例が逆関数になっていると言ってよいxの範囲は制限されることになる。これも、確認しよう。

　他の授業で「写像」って言葉が出てきたんですが、「関数」とは何が違うんですか？

　「写像」の方が「関数」より広い意味に取られることが多いですね。関数は数→数という対応によく使われるけど、写像だともっと抽象的な図形→図形みたいなのにも使ってよいです。どちらにしろ対応関係を表すのは同じです。

　「逆関数」へ

逆関数

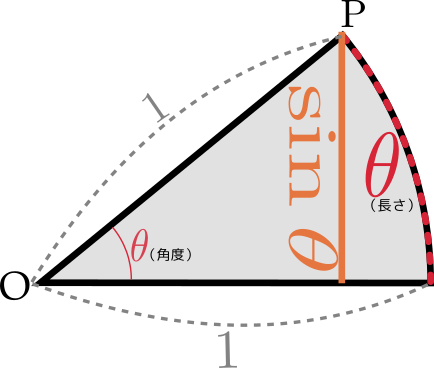
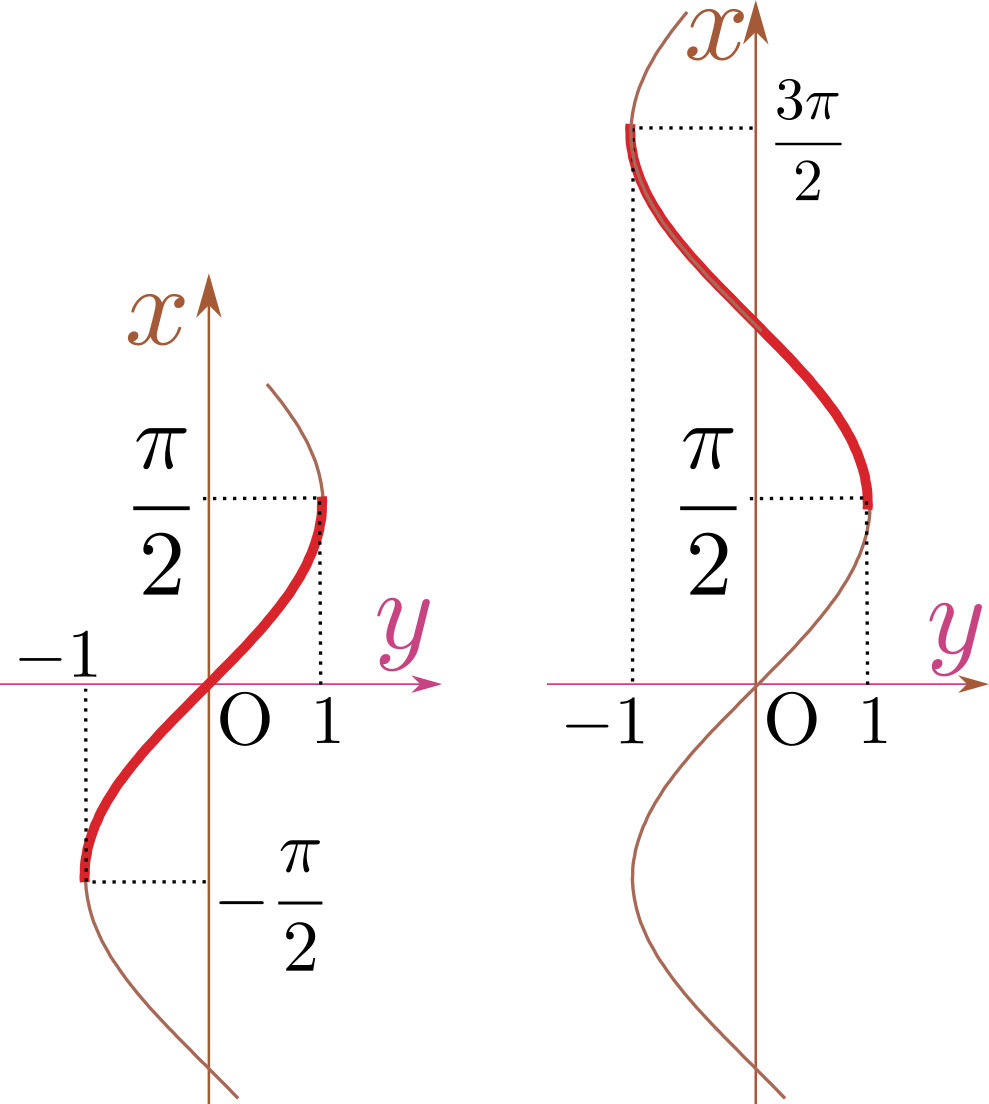　x→yという対応に対してこの逆のy→xという対応を元の関数の「逆関数」と呼ぶ$y=f(x)$に対して${x}=f^{-1}({x})$と書くこともある。。

　たとえば${y}=2{x}$、すなわちあるxに対しその2倍を対応させる関数の逆関数は${x}={1\over 2}{y}$、すなわち、あるyに対しその${1\over 2}$倍を対応させる関数である。この${x}={1\over 2}{y}$という書き方では、独立変数がyで従属変数がxだということになる。前にも書いたように「独立変数にx、従属変数にyを使うことが多い」のは単なる慣習であり、こだわる必要は何もない。もしどうしても「独立変数はx、従属変数はy」という形にしたければ、「ここでxとyを取り替えます」と宣言した上で${y}={1\over 2}{x}$と書き直せばよいそれで何か本質的なことが変わるわけではない。自然科学ではむしろ「この文字は何を表すか」（質量だったり、圧力だったり温度だったり時間だったり）の方が大事なので、同じ量なら従属変数だろうが独立変数だろうが同じ文字を使い、取り替えたりしない事が多い。。

　$y=f(x)$の逆関数が$x=f^{-1}(y)$だとすると、それ逆じゃなくて元のままじゃないですか？

　ええ、この式自体は全く、同じ式です。この場合の「逆」ってのは最初は「$x$が独立変数（先に決まる数）で$y$が従属変数（後から決まる数）」だったのに、後で「$y$が独立変数（先に決まる数）で$x$が従属変数（後から決まる数）」というふうに、独立←→従属の役割分担が「逆」になったというふうに理解してください。

　逆関数を考える時にも定義域と値域に対する注意は必要である。たとえば、「${y}={x}^2$という関数の逆関数は${x}=\sqrt{{y}}$」と言いたくなるが、これは${x}\geq0$という範囲で考えないと正しくない。${x}<0$の範囲であれば、「${y}={x}^2$という関数の逆関数は${x}=-\sqrt{{y}}$」となる。つまりxの領域によって逆関数の形を変えてやらなくてはいけない（これはすぐ下で述べる「関数が1対1か？」という問題のせいでもある）。また、${y}=\sin{{x}}$の逆関数は${x}=\arcsin {y}$と書く（$\arcsin$は「アークサイン」と読む）のだが、${x}=\arcsin {y}$のyは$-1\leq{y}\leq1$の範囲になくてはいけない（こう書いた時にはyは独立変数なので、この範囲は「定義域」である）。

　もう一つ、逆関数を考える時に気をつけなくてはいけないのは、元の関数が「1対1対応」かどうか、という点である。たとえば${y}=a{x}$（逆関数は${x}={1\over a}{y}$または${y}={a\over {x}}$（逆関数は${x}={1\over a{y}}$）などは、一つのxに対応するyはただ一つであり（でなかったらそもそも関数ではない）、さらに一つのyに対応するxもただ一つである。

　しかし、上でも例にした${y}={{x}^2}$はそうではない。たとえば${x}=1$でも${x}=-1$でも${y}=1$になってしまうから、x二つとy一つが対応している（${x}=0$を除く）。このような場合には${x}\to {y}$は関数であるが、${y}\to{x}$は関数ではない。このような場合は前に書いたように、定義域を制限するか、代表を一つ取り出すことでyに対してxが一つだけ決まるようにする。${y}={{x}^2}$の場合であれば、${x}\geq 0$の範囲しか考えないことにすればよい。

　より深刻な「1対1対応でない例」が${y}=\sin{{x}}$の逆関数${x}=\arcsin {y}$である。${y}=\sin{{x}}$は$x$に$x+2n\pi$（$n$は整数）を代入しても値が変わらない。つまり、y一つ（ただし、$-1\leq {y}\leq 1$）に対して無限個のxが対応してしまう。

　では、ここで${y}=\sin {x}$と${x}=\arcsin{y}$のグラフを描いてみよう。

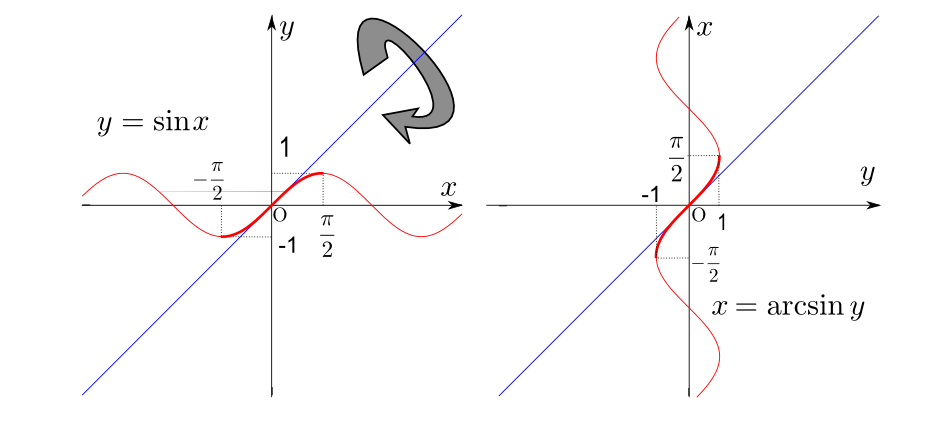
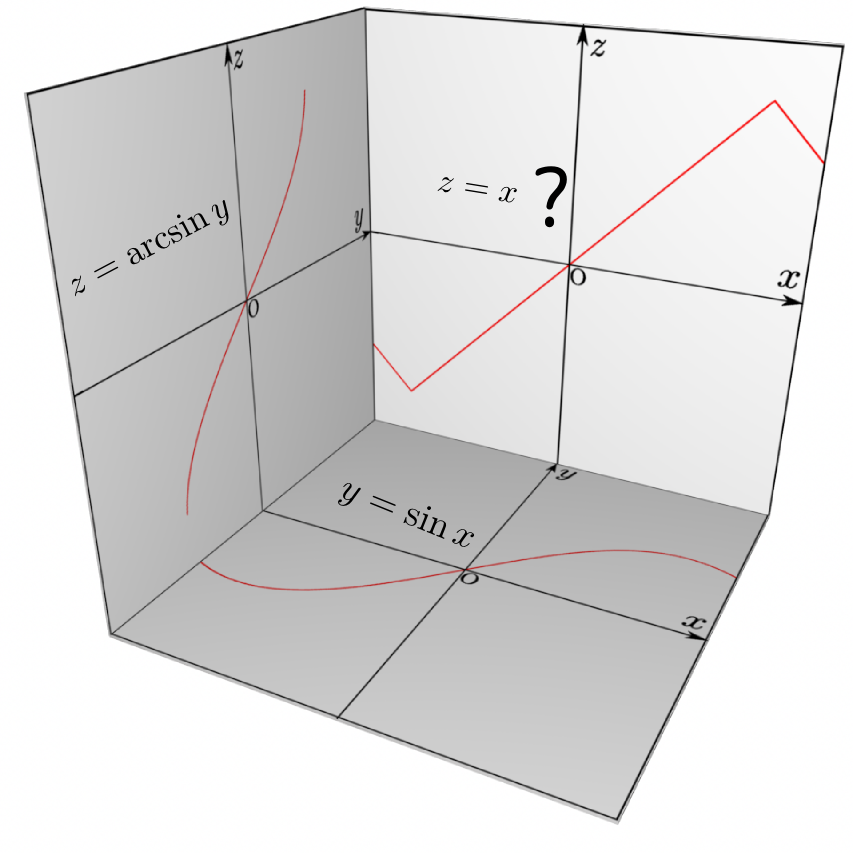
　関数と逆関数のグラフの関係は、（独立変数と従属変数の役割を取り替えるものだから）上の図に示したように「${y}={x}$の線、つまり斜め45度$\left({\pi\over 4}\right)$の線を対称線にして折り返す」ことで得られる。しかしこのままでは、${x}=\arcsin{y}$の方が関数になっていない。一つのyに対しxがたくさんあるからである。そこでグラフのうち太い線にした部分$-{\pi\over 2}\leq {x}\leq {\pi\over 2}$だけを取り出して、残りは捨てることにする。結果、${x}=\arcsin{y}$の定義域は$-1\leq {y} \leq 1$、値域は$-{\pi\over 2}\leq {x}\leq {\pi\over 2}$だということになる（こうしないと一つのyに対して一つのxが対応しない）ここで、xのうちどの部分を選ぶかには任意性があるが、対称性のよい$-{\pi\over 2}\leq {y}\leq {\pi\over 2}$を使うことが多い。。

　この二つの関数を合成するとこれはx=xに戻る…と期待したいところだが、そうはいかない。右に${y}=\sin {x}$と${z}=\arcsin{y}$（まだ元に戻るとは限らないから左辺はxにせず新しい変数zとした）のグラフが合成されるとどのようになるかを描いた。順番に見ていくと、${y}=\sin {x}$という関数の「答え」は$-1\leq {y} \leq 1$の範囲である。さらに${z}=\arcsin {y}$という関数による「答え」は$-{\pi\over 2}\leq {z}\leq {\pi\over 2}$に制限されてしまう。

　つまり元々のxの範囲は任意の実数であったのに、二つの関数を（元に戻ると期待して）作用させた結果、$-{\pi\over 2}\leq {z}\leq {\pi\over 2}$に制限された答えが返ってきたということである。よって、この範囲であれば確かに$\arcsin$は$\sin$の逆関数になっている（グラフの形からわかるように、1対1対応にするためにはこんなふうに変数の領域を制限する他はない）。逆関数を作る時にはこの点に注意が必要である。

　$x$の範囲ですが、$\sin$が下がるところを使ってもよいんですか？

${\pi\over2}$＜$x$＜${3\pi\over2}$ってことね。もちろんいいです。その場合、グラフは下の右側のようになります（比較してください）。

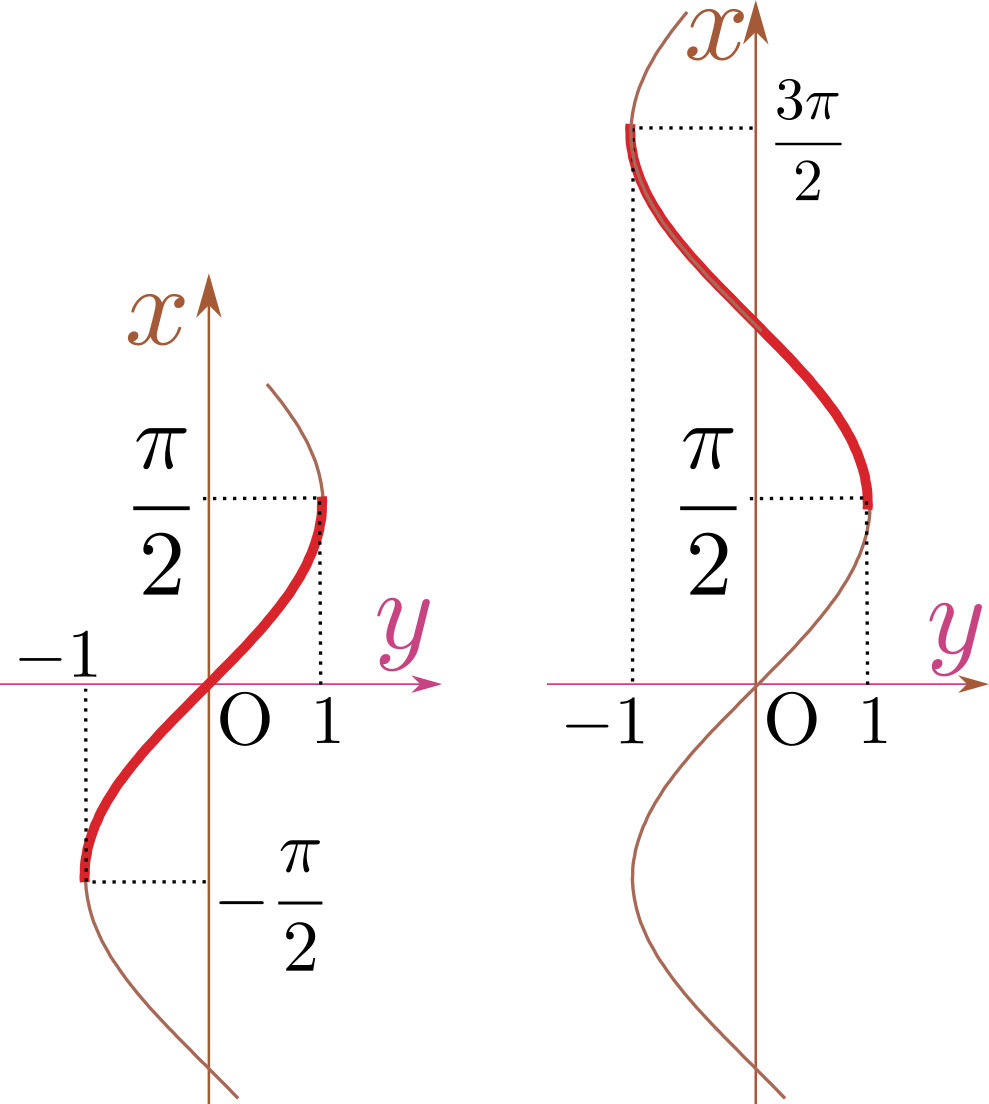
　こういう逆関数も、状況によっては必要になります（たとえば最初から角度がこの範囲にあるとわかっている場合など）。まぁたいていの場合、欲しい角度は$x=0$付近ですが。

　${y}=\cos{x}$の逆関数は${x}=\arccos{y}$である（$\arccos$は「アークコサイン」と読む）。こちらも変数の範囲に注意が必要だが、ここではグラフだけを載せておこう。

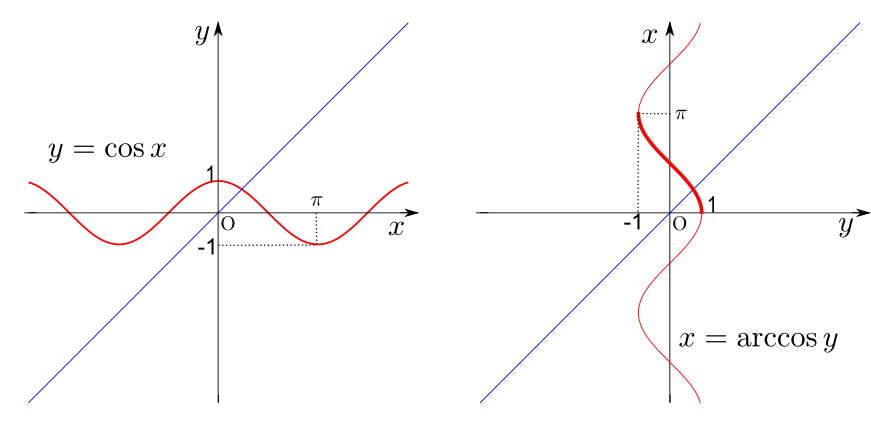
　$y=\arccos x$の値域は$0\leq y \leq \pi$にすることが多い。$\tan$の逆関数である$y=\arctan x$もある。

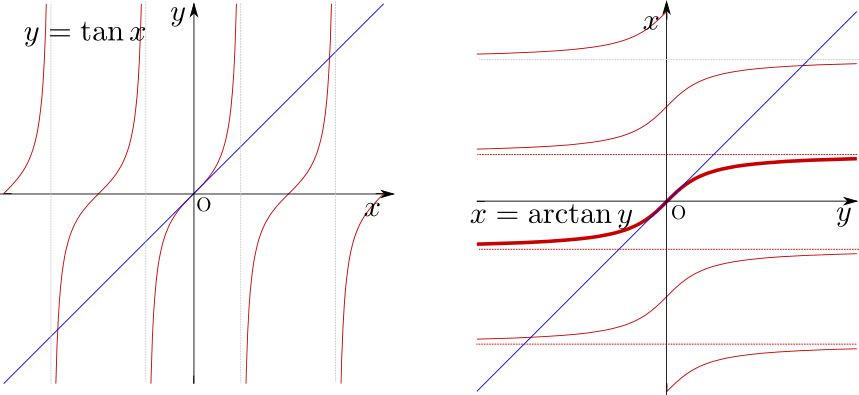
　$\arctan$は「アークタンジェント」と読む。値域は$-{\pi\over 2}<{y}<{\pi\over 2}$とすることが多い。グラフからわかるように、$\tan {x}$のグラフは同じ形の繰り返しだが、その一つだけを取り出して考えないと、逆関数は定義できない。

で距離$L$と角度$\theta$がわかっていれば高さ$h=L\tan\theta$がわかるという話だったけど、逆に$L,h$がわかっていて角度$\theta$を求めたい、ってときは$\arctan$の出番なわけです。このとき、$\theta$が0から${\pi\over2}$の間の角度だということは最初からわかっているから、この範囲で求められれば十分なわけです。

「合成関数」に戻る 「受講者の感想・コメント」へ

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

　主なもの、代表的なもののみについて記し、回答しています。