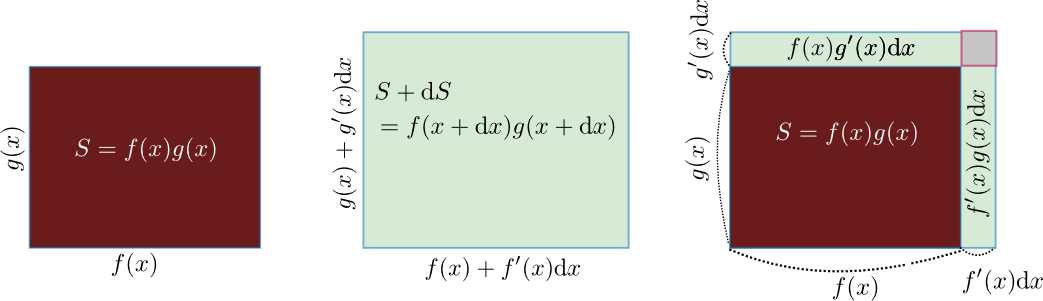微分の性質・公式など
微分の意味
もう一度微分の定義を、以後で使いやすい形でまとめると、
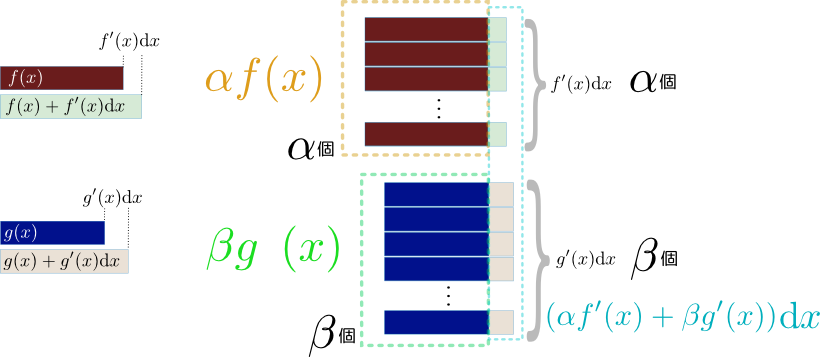
$\underbrace{f(x+\mathrm dx)}_{変化後の量}=\underbrace{f(x)}_{元の量}+ \underbrace{f'(x)\mathrm dx}_{変化量}$
のように書くことができる。この$\mathrm dx$の前の係数$f'(x)$が「$f(x)$の導関数(微係数、または微分)」と呼ばれる量である。となる。
$\mathrm d $という記号
${\Delta x}$や${\Delta y}$は「変化量」という意味があった。微分を行う時は、${\Delta x}$を0に近づける(連動して、${\Delta y}$も0に近づく)。このようにここから先の計算ではしばしば、${\Delta x}$や${\Delta y}$に「変化量」という意味に加えて「0に近づく」という属性が加わる。この「0に近づけていく変化量」という量を表すために、新しい記号として$\mathrm dx,\mathrm dy $を導入しよう。つまり、$\Delta$の替りに$\mathrm d $という記号を使って後で$\to0$という極限を取ることが約束されている変化量を示すことにする。本講義で$\mathrm dx $とか$\mathrm dy$ のように$\mathrm d $のついた量は、すべて「微小変化」を表現する量である。
$\mathrm dx$や$\mathrm dy$を「微小変化」と呼ぶが、この呼び方は少し説明が不足していて、単に「微小」ではなく「0になる極限を取る」という点が重要である。
あるいは「微小」という考え方がしっくりこない、という人は以下のように考えてもよい。
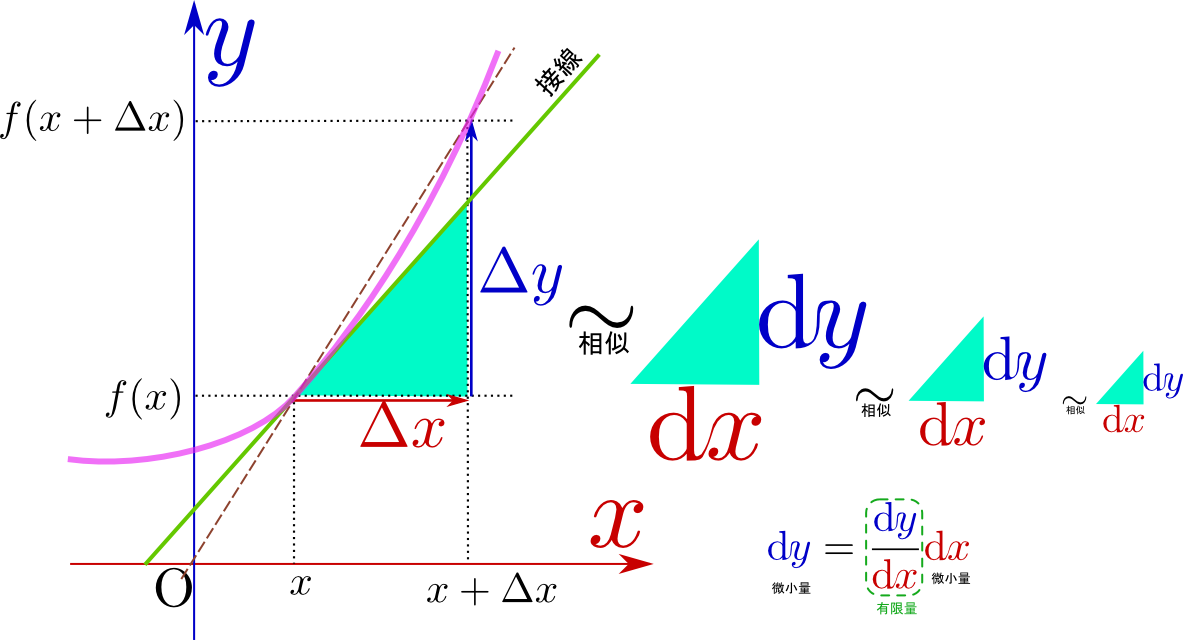
上の図にも示したように、$\mathrm dx$や$\mathrm dy$はあくまで、 のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える(この考え方なら微小である必要はない)。そして、$\mathrm dx$ や$\mathrm dy $そのものの大きさは重要ではなく、
のような「接線と同じ傾きを斜辺とした直角三角形」の底辺と高さだと考える(この考え方なら微小である必要はない)。そして、$\mathrm dx$ や$\mathrm dy $そのものの大きさは重要ではなく、 という形(どんな直角三角形か?)、あるいは「$\mathrm dx$ と$\mathrm dy $の比」が重要であって、$\mathrm dx$ や$\mathrm dy $そのものは大きさを考えてはいけない(考えても意味はない)量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy $の二つで向きを表現する量」なのである。
という形(どんな直角三角形か?)、あるいは「$\mathrm dx$ と$\mathrm dy $の比」が重要であって、$\mathrm dx$ や$\mathrm dy $そのものは大きさを考えてはいけない(考えても意味はない)量とする。いわば、「接線上で定義された長さのようなもの」が$\mathrm dx$ と$\mathrm dy$ であり、それぞれ一つだけでは意味がなく、「$\mathrm dx$ と$\mathrm dy $の二つで向きを表現する量」なのである。
${\mathrm dy\over \mathrm dx}$は普通の数(大きさを考える意味がある)だし、$\mathrm dy=a\mathrm dx$と書いた時の$a$も普通の数である。だから${\mathrm dy\over \mathrm dx}=2$や$\mathrm dy = 0.7\mathrm dx$は意味のある式である。しかし、$\mathrm dx=1$とか$\mathrm dy=0.02$などという式には全く意味がない=0だけは、「$\mathrm dx=0$の極限をとって」のように使うこともあるが、本来はあまりよい使い方ではない。。$\mathrm dy$ や$\mathrm dx $は、二つがペアになって接線の向きを表現している量であって、$\mathrm dx$ のみの大小を云々してはいけない。
新しい記号を使えば、接線の傾きは${\mathrm dy\over \mathrm dx}$になる$\mathrm dx$や$\mathrm dy$は、接線という直線の上での長さを表現しているという考え方もできる。。この${\mathrm dy\over\mathrm dx}$、厳密に書けば
\begin{equation} {\mathrm dy\over\mathrm dx}=\lim_{{\Delta x}\to0}{{\Delta y}\over {\Delta x}} \end{equation}が導関数(もしくは微係数)である。$\mathrm dy$ と$\mathrm dx $は微小量、すなわち0になる極限を取るべき量だが${\mathrm dy\over \mathrm dx}$は有限な量である。
これで${\mathrm dy\over \mathrm dx}$という量が「接線の傾き」という数字として意味のある量となったので、${\mathrm dy\over \mathrm dx}$で一つの量、として扱うことにする。この量もまた$x$の関数であることを表現するため、${\mathrm dy\over \mathrm dx}(x)$のように$(x)$という引数を付けて書く。この書き方はf(x)の$f$のところに${\mathrm dy\over \mathrm dx}$が入った形で、${\mathrm dy\over \mathrm dx}$が「関数名」として機能している(だから、${\mathrm dy\over \mathrm dx}$で1文字であるかのごとく扱う)${\mathrm dy\over \mathrm dx}$は「でぃーわいでぃーえっくす」と分子・分母の順にいっきに(「これで一文字だよ」って感じで)読む。分数のようなものではあるが、「でぃーえっくす、ぶんの、でぃーわい」とは読まない。。
これが導関数(もしくは微係数)を${\mathrm dy\over \mathrm dx}(x)$のように書く理由である。f'(x)の方はニュートンによる記号で、$f$という関数から$f'$を作ったということをよく表現できている記号である。一方${\mathrm dy\over \mathrm dx}$はライプニッツの記号で、何の変化と何の変化の比を考えているのかがよく表現できている記号である。これらの記号は使いどころによって一長一短がある。
この${\mathrm d \over \mathrm dx}$のような記号$y$で微分する${\mathrm d \over \mathrm dy}$などもあるし、ずっと後では偏微分${\partial\over \partial x}$などのような微分演算子も出てくる。を「微分演算子(differential operator)」と呼ぶさらには${\mathrm d \over \mathrm dx}$と書くのも面倒臭がって$D$一文字で表すこともある。。
新しい記号$\mathrm d$を使って微分の計算を行ってみよう。
前に行った$f(x)=x^2$の微分を例としよう。まず、$ {\Delta y}=2{x\Delta x}+({\Delta x})^2$を
\begin{equation} \mathrm dy=2x\mathrm dx+(\mathrm dx)^2 \end{equation}と書きなおす。この式の$\mathrm dx\to0,\mathrm dy\to0$の極限を考えると
\begin{equation} \underbrace{ \mathrm dy}_{\to0} = \underbrace{2x\mathrm dx}_{\to0} + \underbrace{(\mathrm dx)^2}_{\to0} \end{equation}となって0=0という「当たり前すぎてつまんない(trivialな)式」が出る。何の情報も引き出せない。$\mathrm dy$と$\mathrm dx$の比のみが重要なのだから、まず両辺を$\mathrm dx$で割って
\begin{equation} {\mathrm dy\over\mathrm dx} = 2x + \mathrm dx \end{equation}とした後に$\mathrm dx\to0$という極限を取ることで、以下の式を得る。
\begin{equation} {\mathrm dy\over\mathrm dx} = 2x \end{equation}「$\mathrm dx$というのは$\mathrm dx\to0$という極限を取られることを運命づけられている量であることを考えると、右辺第二項の$(\mathrm dx)^2$をこれ以上計算する必要はない」と考えて
\begin{equation} \mathrm dy= 2x\mathrm dx \end{equation}として${\mathrm dy\over\mathrm dx}=2x$を出してもよい。というより慣れてきたらそうするべきである。
$y=x^2$の両辺を微小変化させると
\begin{equation} y+\mathrm dy = (x+\mathrm dx)(x+\mathrm dx) \end{equation}になる。そして「あ、この中には$x\mathrm dx$が2個あるな」と考えれば、右辺は$x^2+2x\mathrm dx$となる。
次に図解で考えよう。一辺$x$の正方形の面積Sは$S=x^2$という式で表現できる$y=x^2$ではなく${S}=x^2$としたが、これはこの図の場合$x^2$に「面積」という意味があるからである。どんな文字を使うかは本質とは関係ない。。この式を微分した結果の導関数が${\mathrm dS\over \mathrm dx}(x)=2x$であることは、
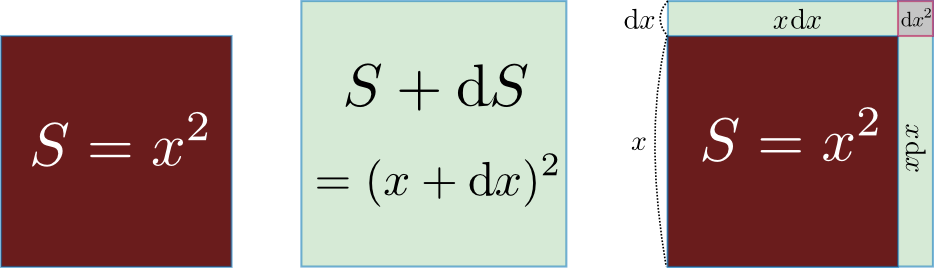
という図から理解できる。この場合、正方形の「縦」の変化による面積変化$x\mathrm dx$と、「横」の変化による面積変化$x\mathrm dx$の足算が面積変化$2x\mathrm dx$となっている。$\mathrm dx^2$の部分は無視されている。
$y=x^3$の微分を図で考えるとすると立方体が大きくなるところを想像するとよい。
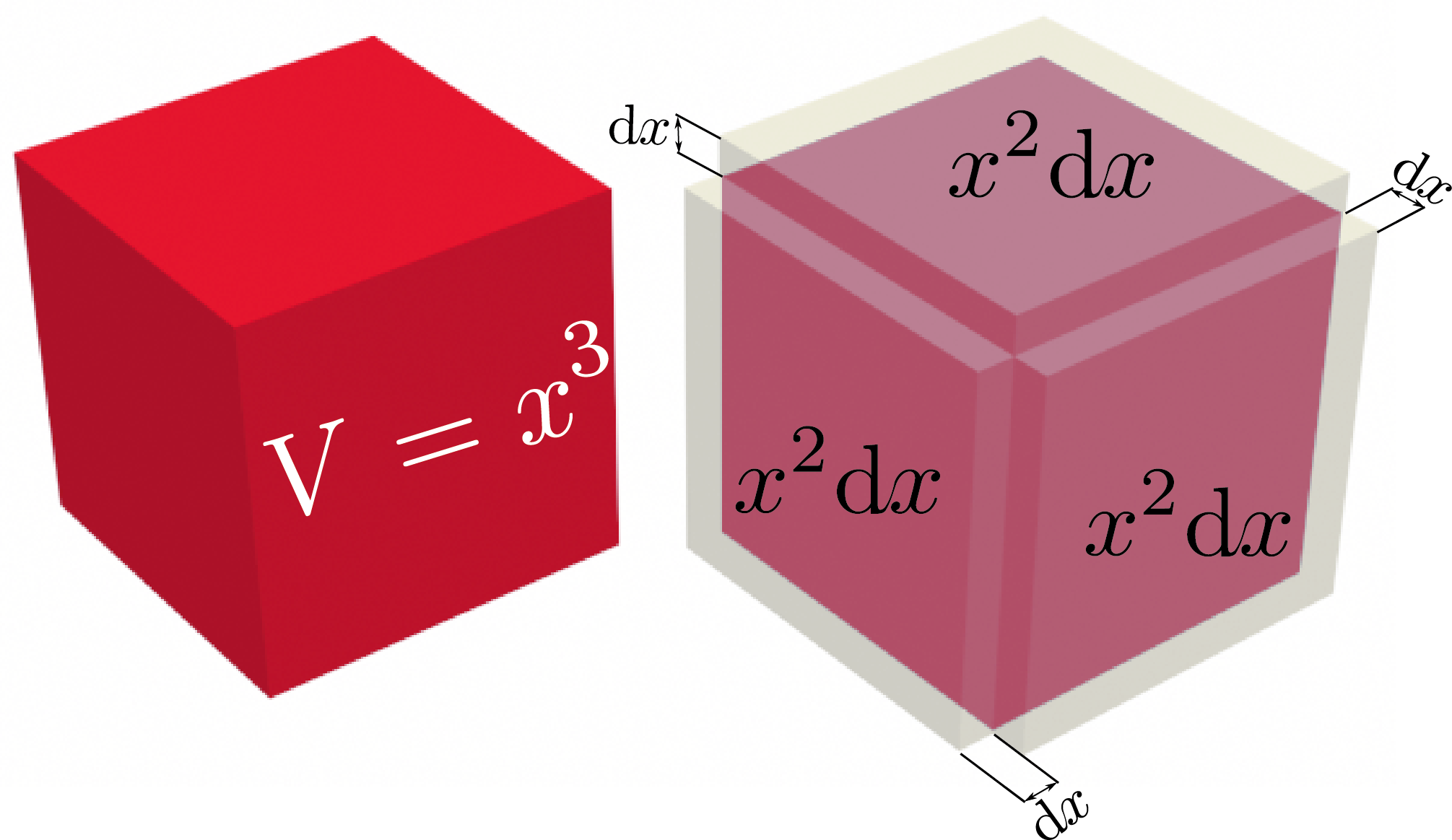
式で考えるならば、
\begin{equation} y+\mathrm dy = (x+\mathrm dx)(x+\mathrm dx)(x+\mathrm dx) \end{equation}として、右辺に$x^2\mathrm dx$が三つある、ということを数えれば、
\begin{equation} \mathrm dy = 3x^2 \mathrm dx \end{equation}となる。そしてこれから$y'={\mathrm dy\over \mathrm dx}=3x^2$である。
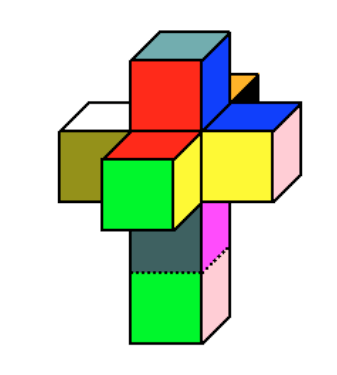
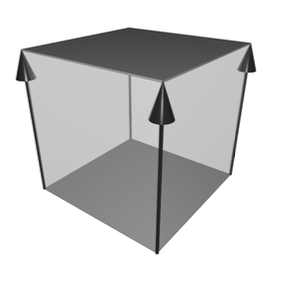
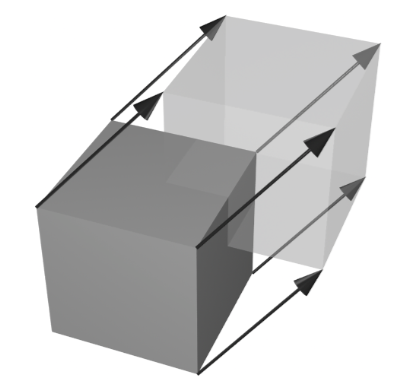
- x^2の微分の2xの係数を二倍した4は、正方形の境界の線の数。
- x^3の微分の3x^2の係数を二倍した6は、立方体の境界の面の数。
- x^4の微分の4x^3の係数を二倍した8は、4次元立方体の境界の立方体の数。
のように考えても、4次元立方体には、8個の3次元立方体が含まれていることがわかる!
冪の微分
$x^2,x^3$の場合をここまで考えたが、$x^n$の微分も同様に
\begin{equation} {y}+\mathrm dy=\underbrace{({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)\cdots }_{n個} \end{equation}の中にある$\mathrm dx$の1次は$n$個の${x}^{n-1}\mathrm dx$であろうと考えるか、もしくは
\begin{equation} \underbrace{{y}}_{これが変化すると}=\underbrace{\overbrace{ {x}\times{x}\times{x}\times{x}\times{x}\times{x}\times{x}\times\cdots }^{n個}}_{\tiny このうち一つが\mathrm dx 変化したもの\atop が全部でn種類出てくる} \end{equation}と考える(二つ以上の${x}$が変化して$\mathrm dx$になったものは、${\cal O}(\mathrm dx^2)$となって出てこない)と、
\begin{equation} \mathrm dy = n{x}^{n-1}\mathrm dx~~~すなわち、{\mathrm dy\over \mathrm dx}= n{x}^{n-1} \end{equation}と分かる。
上の式は$n$が自然数なら正しい。では、指数が負の整数ならどうなるだろうか。その場合は、${y}={x}^{-n}$をまず、${x}^n {y}=1$に直してから、その微小変化を考えると、
\begin{equation} \begin{array}{rll} \underbrace{({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)\cdots }_{n個}\times({y}+\mathrm dy)=&1\\ \underbrace{{x}^n {y}}_1 + n{x}^{n-1}\mathrm dx{y} + {x}^n \mathrm dy =&1\\ {x}^n \mathrm dy =&-n{x}^{n-1}\mathrm dx \underbrace{{x}^{-n}}_{{y}} \\ \mathrm dy =& -n {x}^{-n-1}\mathrm dx\\ \end{array}\label{fubekibibun} \end{equation}となる慣れてきたら、「${x}^n {y}=1$の両辺を微分する」の一言で$n{x}^{n-1}\mathrm dx {y}+ {x}^n \mathrm dy =0$を出してよい。(結果${\mathrm dy\over \mathrm dx}= -n x^{-n-1}$を上の${\mathrm dy\over \mathrm dx}=nx^{n-1}$と見比べると、単に$n\to -n$と置き換えただけの式になっている)。
指数が整数でない場合についても考えよう。たとえば${y}={x}^{1\over n}$については、これをまず${y}^n = {x}$になおしてから、
\begin{equation} \underbrace{({y}+\mathrm dy)({y}+\mathrm dy)({y}+\mathrm dy)({y}+\mathrm dy)\cdots }_{n個}= {x}+\mathrm dx \end{equation}とすれば(これまで同様、1次のオーダーを取り出すことで)こちらも慣れてくれば、${y}^n = {x}$からすぐに$n {y}^{n-1}\mathrm dy = \mathrm dx$が出せるだろう。、
\begin{equation} \begin{array}{rl} n {y}^{n-1}\mathrm dy =& \mathrm dx\\ {\mathrm dy\over \mathrm dx} =& {1\over n {y}^{n-1}}={1\over n}{x}^{{1\over n}-1}\\ \end{array} \end{equation}がわかる。同様に、${y}={x}^{m\over n}$に関しても${y}^n={x}^m$としてから
\begin{equation} \begin{array}{rl} \underbrace{({y}+\mathrm dy)({y}+\mathrm dy)({y}+\mathrm dy)({y}+\mathrm dy)\cdots }_{n個}=& \underbrace{({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)({x}+\mathrm dx)\cdots }_{m個}\\ n{y}^{n-1}\mathrm dy =& m {x}^{m-1}\mathrm dx \end{array} \end{equation}のように考えれば、
\begin{equation} {\mathrm dy \over \mathrm dx}= {m\over n} {x}^{{m\over n}-1} \end{equation}が示せるから、一般の有理数$\alpha={m\over n}$に対して${y}={x}^\alpha$の微分は
\begin{equation} {\mathrm dy\over \mathrm dx}= \alpha {x}^{\alpha-1} \end{equation}としてよい。ここまでくれば、「無理数に対しても極限操作で定義すればよさそうだ」とわかる(たとえば、$y=x^\pi$の微分を計算したければ、それは$y=x^{3.14}$の微分に近く、こちらは$y'=3.14x^{2.14}$のように微分できる)で、$\alpha$は任意の実数でよい。この式を見ると微分により${x}$の冪を1ずつ下がることが言える。例外は定数(すなわち$x^0$の時)で、この時だけは$(定数)\times x^{-1}$とはならず、0となるでは微分すると$x^{-1}={1\over x}$になる関数はないのかというと、ちゃんとある。。