ここまでの流れ

1. 等温操作における最大仕事でヘルムホルツの自由エネルギーを定義した。
   $-W_{\rm max}=\Delta F$
   ↑ヘルムホルツ自由エネルギーが減った分だけ外に仕事ができる、ということ。
   この定義では、（等温操作で定義したので）温度が変化した時の$\Delta F$に関しては何も言ってないことに注意。
2. 断熱操作における仕事で内部エネルギーを定義した。
   $-W=\Delta U$
   ↑内部エネルギーが減った分だけ外に仕事ができる、ということ。
   こちらは断熱操作（準静はつかない）で成り立つ式なので、全ての変化に対して定義できることに注意。
3. 等温操作での「吸熱」を$\Delta U-\Delta F$で定義した。
4. さらに、$S={U-F\over T}$でエントロピー$S$を定義した。
5. ここで、$F$が温度変化によってどう変わるかはまだ定義してなかったので、断熱操作では$S$が変化しないという条件を置いて$F$の温度依存性を決定した。これにより、エントロピー$S$が「断熱変化で変化しない状態量」になった。

　4.の段階では、カルノーサイクルの等温操作における$\Delta S$（$S$の変化）が同じになるが、断熱操作でどうなるかについてはまだわかってない。5.で$F$の温度依存性を決めたことで、断熱操作では$\Delta S=0$に決まった。

　前回はエントロピーの定義$S={U-F\over T}$を確認し、

• 示量変数であること
• 相加性を持つこと
• 任意の$T$＜$T'$と任意の体積$V$について、$S(T;V)$＜$S(T';V)$が成り立つこと（エントロピーは温度の増加関数だということ）。
• （それぞれの変数が微分可能なら）$\displaystyle {\partial U(T;V)\over \partial T}=T{\partial S(T;V)\over \partial T}$

ということを確認した。

　理想気体の場合で上の手順を具体的にやってみよう。

理想気体の場合のエントロピー

　実例の一つとして、理想気体の場合でエントロピーを計算しておこう。理想気体では、内部エネルギーは$U=cNRT+Nu$（$c$は単原子理想気体なら${3\over2}$）だった（

）。

　ヘルムホルツ自由エネルギーは、$F=-NRT\log\left({V\over V^*}\right)+$（$V$に依存しない部分）ということろまで計算していた（

）。ただし、この段階では$F$の$T$依存性を考えてなかった。教科書に合わせて、

$$F=-NRT\log\left({V\over v(T)N}\right)$$

としておこう。

　この通りに$S={U-F\over T}$を計算すると、

$$S ={cNRT+Nu+NRT\log\left({V\over v(T)N}\right)\over T} =cNR+{Nu\over T}+NR\log\left({V\over v(T)N}\right)$$

となる。まだ決まってない部分はどうやってきめるかというと、前回考えたように、$S$が断熱操作で変化しないように決める。理想気体の断熱操作では、$T^c V$が一定だったから、その条件を満たしつつ$T,V$変化するときに$S$が変わらないようにする。

$v(T)=\left({T^*\over T}\right)^c V^*\mathrm e^{{u\over RT}}$と決める（$T^*$と$V^*$はどこか「基準点」の温度と体積）ことにすれば、

$$S=cNR+NR\log\left({T^cV\over (T^*)^c V^*}\right)$$

となる。この式は確かに示量的（$\log V$のところが気になるかもしれないが、$\log \left({V\over V^*}\right)$とまとめて考えればよい）で相加的で、$S(T;V)$＜$S(T';V)$が成り立つ。また、前回最後に確認した式${\partial U\over\partial T}=T{\partial S\over \partial T}$を確認しておこう。微分すると確かに

$$T{\partial S\over\partial T}=T{\partial(NR\log T^c)\over \partial V}=T\times{cNR\over T}=cNR={\partial U\over \partial T}$$

になっている（なお、$S$のうち$T$によらない部分はどうせ微分しても消えるので、$S$のところには$NR\log T^c$だけを代入している）。

エントロピーと可逆性・不可逆性

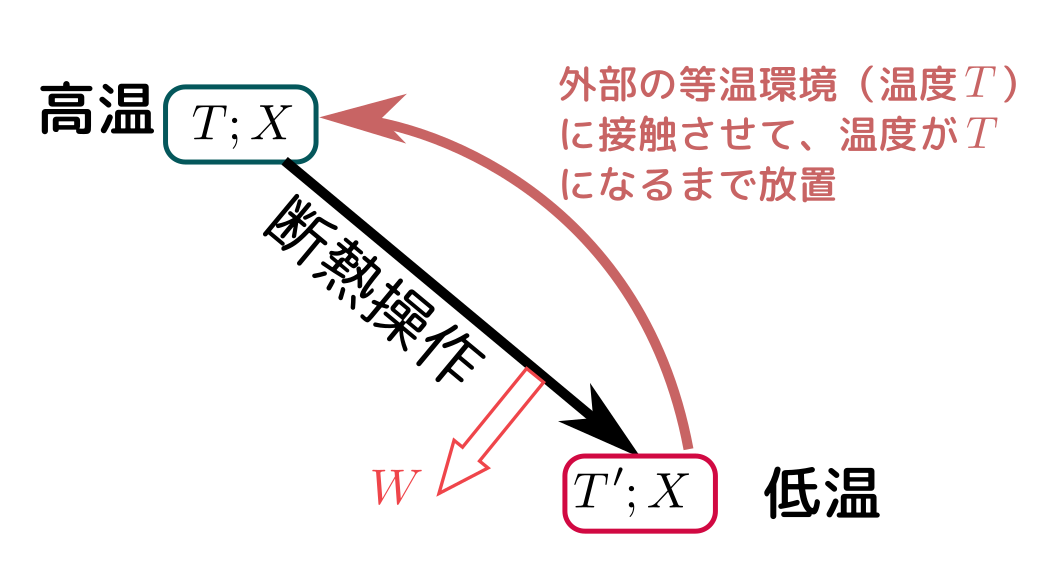
断熱操作$(T;X){{\rm a}\atop\longrightarrow}(T';X')$が可能でも、この逆操作である断熱操作$(T';X'){{\rm a}\atop\longrightarrow}(T;X)$が可能とは限らない（可能な場合はこの操作は可逆であると言う）。

　不可逆であることがすぐわかる例として、

がある（示している内容はとても単純で「寒い時に仕事をしてあたたまることはできるが、逆は無理」ということだ）。

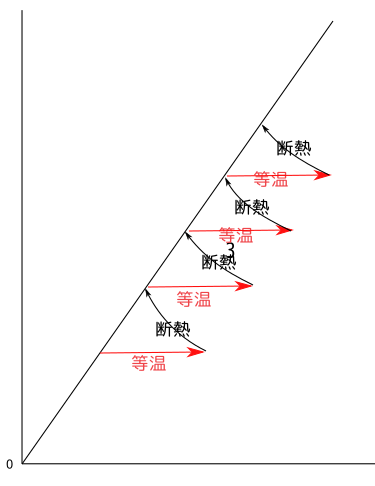
この原理はKelvinの原理を使って以下のように示される。

　上のようなサイクル（温度$T$の環境としか熱のやりとりをしてない）は、断熱操作において自分のエネルギーを下げている（高温→低温）ので、必ず正の仕事をする（環境と接触して温度変化する時点ではまったく仕事をしない）。しかしこれはKelvinの原理に反するから、こんなことはできない。

　この時「（示量変数$X$を変えずに）温度を上げる」という操作は「エントロピーを上げる」という操作と同じ（${\partial U\over \partial T}=T{\partial S\over \partial T}$で、この量は正。もちろん$T$は正だから、${\patial S\over \partial T}$も正）だということに注意しよう。ここで示したのは示量変数を変えない方向の変化である（後で一般化する）。

　以上の結果をグラフで表現すると、$V$-$T$グラフ

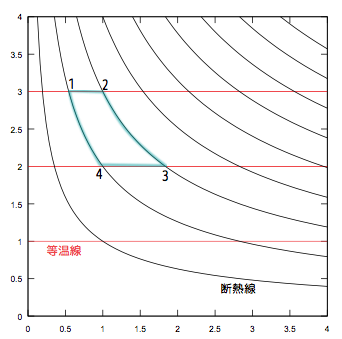
において「真上（$V$を変えずに$T$を上げる）ことはできるが、真下には行けない」ということを示したことになる。これをもっと一般的にする。

　まず$S(T;X)\leq S(T';X')$なら操作が可能であることを言う。断熱準静的操作を行えば$S$を上げずに示量変数$X$（たとえば$V$）を変えることができる。

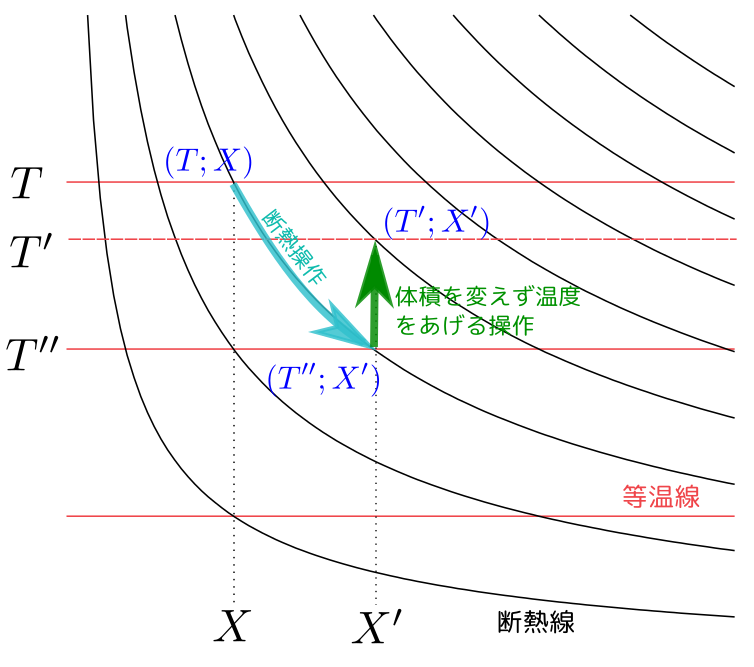
　つまりグラフの断熱線の上ならいくらでも移動できる。よって、まず断熱線に沿って$S(T;X)$から$S(T'';X')$まで行く（断熱膨張なので温度は下がるだろう）。$T''$＜$T'$なら、その後$T''\to T'$へと温度を上げればよい（上げるのはいつでもできる）。逆に温度を下げることはできないから、$T''$＞$T'$ならその操作はできない。

　次に、断熱操作$(T;X){{\rm a}\atop\longrightarrow}(T';X')$が可能なら$S(T;X)\leq S(T';X')$であることを示そう。

　今度は、可能だと仮定した断熱操作で$(T;X)\to(T';X')$と変化させた後、断熱準静的に$(T';X')\to (\tilde T;X)$と$X$だけを戻す。Planckの原理から$T\leq \tilde T$だから、この一連の変化で温度は上がり、ということはエントロピーは増える。断熱準静操作ではエントロピーは増えないから、その前の断熱操作の間に増えていることになる。

　こうして「断熱準静操作で変化しないような状態量」として定義したエントロピーは、実は（なぜそうなったのかというとKelvinの原理またはPlanckの原理のおかげだが）さらに「断熱（準静的とは限らない）操作では減らない（変わらないか、増えるか）」という興味深い性質を持っていることがわかった。

　結局、「断熱線（$S$が一定の線）」、言わば「等エントロピー線」を考えて、その等エントロピー線による「山を登る」方向にしか移動できないことになる（↓の図で、色をつけた部分にしかいけない）。緑の矢印は、可能な経路の例である。

　なお、この場合は「温度を下げる操作」も可能である。Planckの原理で必ず温度が上がるのは、体積などの示量変数を固定しているからである。

真空への自由膨張

　気体などが真空に向けての膨張はエントロピー増大過程で（だから不可逆で）ある。それは理想気体の場合のエントロピーの式からもだいたいわかるが、膨張した気体を断熱準静操作で元の体積に戻すにはかならず外部から正の仕事をする（すると内部エネルギーが増える、つまり温度が上がる）。同じ体積ならエントロピーは温度の増加関数だから、エントロピーは増えている。

　理想気体の場合の式を見てみると、確かに$S=cNR+NR\log\left({T^cV\over (T^*)^c V^*}\right)$という量は体積増加により増える量になっている。