青字は受講者からの声、赤字は前野よりの返答です。
今までの力学と熱力学の違いがわかった。高校の物理でも今日の授業くらいはしてもいいのではないかと感じた。
高校で習う範囲の熱力学は最初から準静的に限った話になっている感じですね。
私たちが高校で習ってきた気体の状態方程式はどのような条件下で活用されているか、や等温変化断熱変化での気体がする、される仕事についてもよく理解できました。
まず今日の話(特に最大仕事と準静的)が大事なキーワードになります。
元に戻しただけで仕事をしたことになるものが新しく発見されればいいなと思った。準静的に動かした時、最大仕事が実現できることがわかった。
まぁ、エネルギーが湧いて出るようものはやっぱりないのですよ。
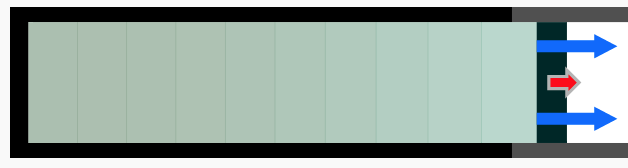
タブレットを使って、等温操作、断熱操作の例を見て、視覚的に準静的な時とそうでない時の温度変化を感じることで今日の授業がわかりやすかった。
準静的とは何で、どうしてそんなものを考えなくてはいけないか、ここが大事です。
ピストンを引いて押しても仕事が0にならないのが面白いなと思いました。最初はイメージが湧きませんでしたが、アニメーションでどのように温度が変化しているのか見れて分かりやすかったです。
現実は初等的な力学の通りにならないというのが面白いところですね。
ピストンによるエネルギーの移り変わりの説明が理解することができ面白かったです。「熱」というよく分からない存在を毎回の授業でとらえていきたいです。
まずは「最大仕事」から入って「ヘルムホルツの自由エネルギー」の意味を知りましょう。そこから熱まではもう少し。
複数の変化が同時にあるので、理解が難しそうだと思いました。
まぁややこしいと言えばややこしいですが、一歩一歩理解していってください。
タブレットを使って、温度を色で見ることができたので気体の温度変化について理解することができた。
今日で「準静的」を考える意味をつかんでおきましょう。
タブレットで理想的極限からのずれを実感できた。現実はうまくいきませんね。
理想通りにいかないのが現実ですが、だから物理を考えるときはまず「理想」を極めるのです。
冷蔵庫は、ポンプを引いて中の温度を下げているということを初めて知りました。プログラムを使用しての授業、とても分かりやすかったし、頭にすんなりと入ってきました。
まぁ実際は液体を気体にする(およびこの逆)過程なども入れて、もう少し複雑なことをやってます。
今までの力学で、今回の授業で例に出た装置で空気を圧縮、膨張させるとエネルギーがバランスすると見ていたのは、空気抵抗や摩擦を無視して考えるように、断熱で準静的操作のときの状態だと都合よく考えていたのかと思った。
まずは理想的な状況を考えて、少しずつ現実に近づけていくのは、物理の常套手段です。
熱力学のおおまかなものがわかった。これから数学を用いて詳しくやると思うが、今日学んだことを忘れずにやっていきたいと思う。
ここから細かく、数学的にきっちりやっていきながら、理解を深めましょう。
初めて聞く言葉もあったが、説明はとても分かりやすかった。ただ、分かった気でいるのかもしれないので、しっかりと復習したいです。
じっくりと教科書読み込んで、考えてみてください。
タブレットを使って、理解が深まった。すごく面白いと思った。力学での「摩擦なし」という条件と、熱力学での「準静的過程」という条件が同じポジション。簡単な状況での現象から考えていく、ということが、しっくりきた!!
熱力学を理解する上での最初の「肝」が「準静的」の理解だと思います。そこがしっくりきてよかった。
「準静的」「最大仕事」という物理の意味が分かった!また、「熱力学第2法則」というものが、エネルギー保存則とは別の熱力学法則で存在する、という大きなポイントが理解できたので、少しだが全体像をイメージできた。
ここからさらに詳しく、熱力学を理解していきましょう。
準静的、最大仕事など熱力学に必要な考えが理解できた。
大事なところです!
「準静的」「最大仕事」など、これからに備えて復習していきたい。
じっくり考えてみてください。
等温過程と断熱過程、準静的であるかどうかの違いでどのようなことが起こるか、少し理解できた。
「準静的」という理想的状態を考えなくてはいけない理由を理解してくれればよいです。
急激にピストンを動かすと理想的な状態から離れてしまう説明が分かりやすく、かつ楽しくて時間がいつの間にか過ぎてました。
楽しく勉強できてよかったです。この後もいろいろ楽しいです。
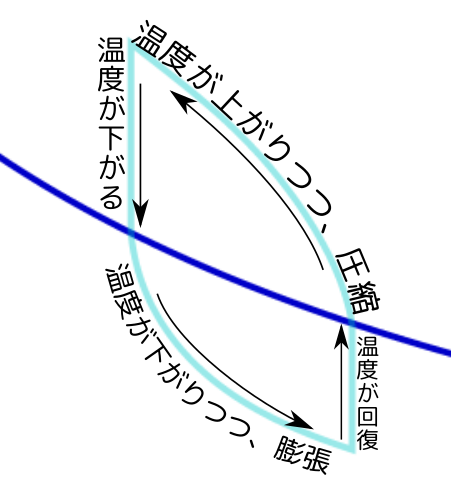
気体の体積を増加させ、次に戻した時、気体が受ける仕事の方が大きいのは、すごいと思った。しかしその分は熱として出るので、うまく成り立っていると思った。
物理の(熱力学の)うまくできているところを、感じてください。
内の人の気持ちになったり、外の人の気持ちになって考えたり、それによってW(仕事)をされる方が変わるので、まちがえないようにしたい。
そこは確かに混乱するかもしれないが、まちがえると物理が変わっちゃうね。
習ったことを、自分の言葉でしっかりと説明できるようにしなければいけないと感じた。等温の状態と断熱の状態での温度の変化の違いや、等温の際の最大仕事、準静的な操作について復習しておく。
復習して「俺ならどう説明する?」ということを考えてみてください。いい勉強になりますよ。
物理における理想状態はないと分かりました。しかし、実際の教授の中には勉強から一切逃げない学問だけがおもちゃという理想の教授はいますか?
さぁ。それは世界中の教授をチェックし終わらないと判定できないような。
実際の熱の移動と理想的状態の違いがわかりやすかった。
ちなみに、実際の熱の移動は今日のプログラムよりも、さらに複雑です。
等温過程の$W_1$と$W_2$の差は放熱と吸熱の差であるということはわかったのですが、その場合、中の気体は外の気体と吸熱放熱のたびに仕事をしているという理解でいいのでしょうか? それとも熱の散逸ですか?
「熱」は仕事でない形でエネルギーが移動している時に使う言葉なので、仕事ではありません。
ピストンの体積の増減、空気の膨張・圧縮で火が点くのも初めて知りました。準静的であるかそうでないかを目で見て実際感じることができました。圧力変化を積分で表そうとしたときに、ピストンの中の温度が場所によって違うのを見て、$PV=NRT$という単純な式で表しきれないのがわかりました。
単純に状態を表し切るためには、「準静的」という理想化が必要になる、ということですね。
準静的と最大仕事について少しわかった。教科書ノートを見て復習すれば理解できると思う。
では、教科書ノートじっくり読み込んでください。
今までに習った物理とは違って、現実の物理現象を相手に頭を悩ませるのは少し新鮮だった。
今までの物理も現実です。ただ、(熱力学でもそうですが)現実そのままだと把握しづらいので、理想化をそれぞれのレベルで行っているのです。
準静的の意味がよくわかってなかったので、今日の講義でよくわかりました。
そこはとっても大事なところです。理解しておきましょう。
教科書読んで復習します。でもストーリーのない教科書は読むのつらいです。
いや、この教科書は結構、ストーリーありますよ。
とっても遅く動けば効率が良いということがわかったが、時間効率はかなり悪そうだから、準静的もまた現実的でなく、世の中うまい話はないんだなぁと思った。
熱力学を勉強していくと、「うまい話ができないように物理ってできてるんだなぁ」とこの先でもおもうかもしれません。
熱の出入りや力学的エネルギーの出入りを、図でわかりやすく説明してくれたので、とてもわかりやすかったです。
この二つをきっちりと理解していきましょう(熱をちゃんと定義するまでだいぶかかるけど)。
等温操作と断熱操作について学んだ。ピストンの動きを速くするか遅くするかで変化の仕方に違いがあることがわかった。
だから、「十分遅く」と理想化することが必要なわけです。
準静的と最大仕事がなんとなく理解することができた。
最初なのでまだ「なんとなく」でもいいけど、反復していくうちに、きっちり理解していこう。
今回は疲れず楽しく授業を受けられた!
理解できたことをもう一度復習して、自分のものにできるようにします。
楽しく、理解していきましょう!
準静的過程と最大仕事について、プログラムで見やすかった。
この二つはこれからの熱力学の勉強で、とっても大事。

 で表現している。
で表現している。 で表現している。
で表現している。