前回の第２回
では準静的操作と最大仕事というキーワードについて、アニメーションなどを見ながら説明した。

まず聞いてみよう---準静的操作とはなんであったか？
じゅうぶんゆっくり動かすことです。
ふむ。ではどうなったら「じゅうぶんゆっくり」なんだろう？---そして、どうしてそうしなきゃいけないんだろう？？
気体が変化についてこれると「じゅうぶんゆっくり」なのでは。
「変化についてこれる」というのはどういう意味？？
ピストンを引いたときに、気体がピストンについてくると仕事をちゃんとしてくれるけど、そうじゃないとできる仕事が減ってしまう、ということです。
うん、いいところをついている。「ちゃんと仕事をしてくれる場合」の仕事を「最大仕事」と言って、熱力学ではそういう状況が成立する理想的状況を考えていく。
　先週も使ったP-Vグラフを今週も使いつつ授業した。今日の講義録にも
P-Vグラフつきのページ
をつけてある。
では、今日は教科書の第２章に沿って、平衡状態の記述について説明していこう。一部内容は３章や４章を先取りして話している。

平衡状態

　熱力学が考える理想的状況をピストンの場合で説明すると、

のように、ピストンを引いた直後の「左が高温・高圧で右が低温・低圧」という状況は「平衡状態」ではない。

　しばらく待つと、

のように全体の温度・圧力（密度も）が一様になり、「平衡状態」に達する。

　というわけで、ざっくり言えば「じゅうぶんゆっくり（つまり準静的に）変化するのであれば、途中の状態もすべて平衡状態を保ったまま変化していくと考えてよい」ということになる。

　平衡状態は温度・圧力などが一様なので、「温度はTです」「圧力はPです」と語ることで状態を指定できるが、平衡でない状態では「左の方の温度はT1で、右に行くほどだんだん低くなって最後はT2に」というふうに、場所の関数である温度変数T(x)を使わないと状態が指定できない。つまり、平衡状態の方が使う変数が少なくて済む。

　こう言うと、楽だからとズルをしているように思えるかもしれない。しかし大事なことは、「考える状態を平衡状態に限る」という（「ズル」に見えかねない）簡単化をしてもなお、熱力学という学問はとても役に立つということだ。たとえば力学における「摩擦がないとする」というのも「ズル」っぽいと言えば「ズル」なのだが、摩擦がないという簡単化をしてなお、力学は豊富な内容と実用性を持っている。

　考えてみると、ミクロな視点で見れば気体は6×1023個ぐらいの分子の集まりだから、「状態を完全に指定」しようと思ったらこの分子一個一個の運動を指定しなくてはいけない。

示量変数

　気体の状態を指定する変数としては温度T、圧力P、体積V、物質量Nなどが思い浮かぶ。このうち体積Vと物質量（モル数）Nは相加的（additive）であるという性質を持っている（たとえば体積V′の系と体積V″の系を合わせるとV'+V''の系になる）。

　体積の相加性は、同成分の物質なら疑うべくもないが、例えば『水1リットルとアルコール1リットルを混ぜると2リットルにならない』（この場合、気体と違って箱に閉じ込めているわけではないので体積は変化してしまう点に注意）のような現象もある（よりわかりやすい例は『大豆１升とゴマ１升を混ぜても２升にはならない』）。

　状態を指定する変数の中で、

系全体の大きさを\lambda倍した時に同じように\lambda倍になる変数

を「示量変数」（extensive varijable）と呼ぶ（漢字の方が意味がわかりやすい）。

　気体の場合、体積Vと物質量（モル数）Nが示量変数である。

　この後「示量変数を変化させる」という操作を行うのだけど、たとえば体積変化を起こすとその手応えは圧力として出現する。

Nを変化させるってのはどういう状況ですか？
　気体が空気なら、シリンダーに空気を吹き込む、ってことになるね。それに応じてもちろん系のエネルギーは変化する（どう変化するんだ、というのはずっと後で）。

　系全体を大きくしても変化しない変数は「示強変数」（intensive variable）である。圧力Pや温度Tはこちらに属する（100度の水と100度の水を合わせたら200度になったらびっくりする）。

熱力学の視点

　熱力学は、「実際には6\times10^{23}程度の自由度がある系」をまじめに考えるという方向の学問ではなく、むしろ、「外部からする操作の種類」程度の数の変数だけで系を代表させて考えていく。

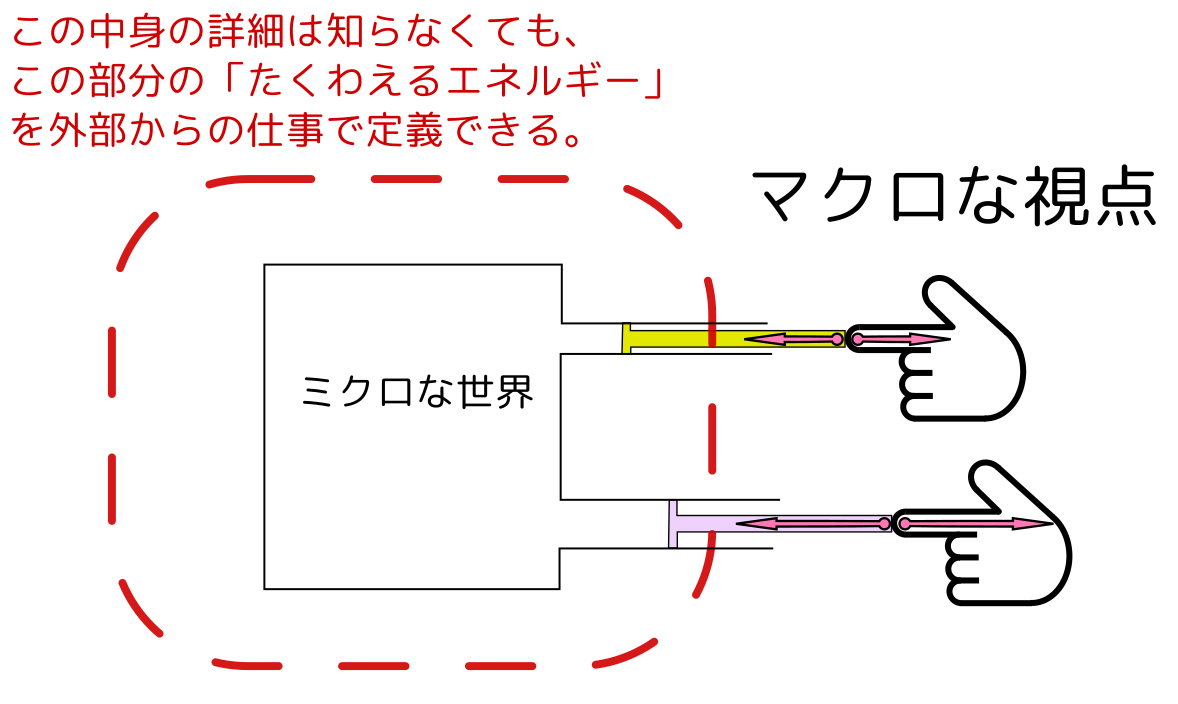
　上の図の場合、操作できるのが二つのピストンがあり、それぞれを押したり引いたりするとどの程度仕事がされるか、ということは「手」の動きと「手応え」で計算できる。それに応じて系のエネルギーに対応するものが増えたり減ったりする（前に説明したようにこの時の仕事は変化のさせ方によって違うからエネルギーをちゃんと定義するには「準静的に」とか「最大仕事になるように」とか変化方法を指定する必要がある）。

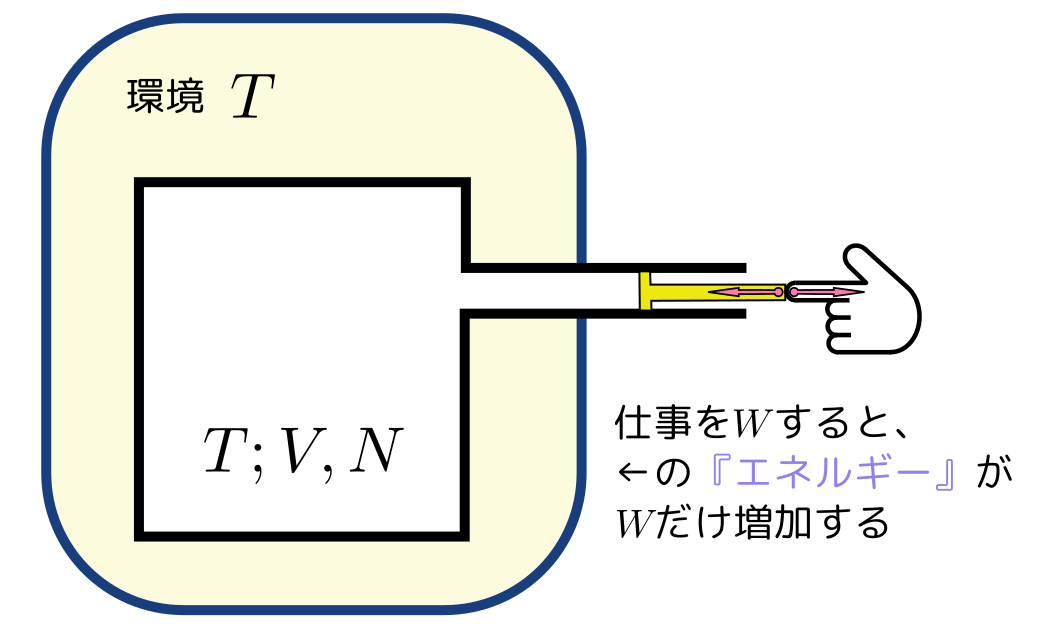
等温環境での平衡状態

　実際に実験を行う時の状況として「実験装置（系）を周囲の温度と同じにする」という状況がある。この時（例によって準静的に変化が起こるとすれば）、系の温度は一定である（実際には変化の最初と最後以外では温度が変わっている可能性はある）。

　ここで「温度って何？」をまだ定義してないのだが、ここでは教科書の要請2.1（ざっと言うならば、「示量変数を固定した状態で十分時間がたてば系は平衡状態に達する」ということ）と、教科書の要請2.2（ざっと言うならば「ある温度の環境の中で平衡に達した系の温度は環境温度と同じになる」といいうこと）を認めて、まわりの環境が「温度」なる量を一定にすべくいろんな影響を与えてくれているとだけ解釈する。
いつかは平衡に達するんだとすると、鉄を手で触るとひんやりするのはなぜですか？
ひんやりするのはまだ平衡に達してない間だけだね。そのうち鉄が生暖かくなって平衡に達します。ちなみに人間の温度（体温）が気温と一緒にならないのは、人間が体温を36度ぐらいで一定になるように頑張っているからであって、その頑張りがなくなれば平衡に達します（「死んだら」ってことだけど）。死ぬまでは平衡に達しないよう頑張りましょう。

　このような系の状態を記述するには、まず「外部から操作できる示量変数」であるX（V,Nをまとめてこう書く）と、「外部環境が決める示強変数」であるTが必要である。つまり、(T;X)（;で分けたのは（示強;示量）ということ）変数で系の平衡状態が定義できる（くどいようだがもう一度、こんなふうに少数の変数で系の状態が指定できてしまうのは、平衡状態だからである）。

　こういう系が等温に保たれる状態で系に仕事をさせると、その分系の『エネルギー』括弧つきで書いたのは、普通のエネルギーとはちょっと違うからである。が変化する。

ここで、このように定義された『エネルギー』が「ヘルムホルツの自由エネルギーF」というものになるのだが、このエネルギーはバネのエネルギーと決定的に違うことが「準静的でないとダメ」という点以外にもう一つある。バネの場合「{1\over2}kx^2というエネルギーは誰が持っているのか？」と言われたら答は間違いなく「バネ」であろう。しかしこの場合、『系』は『環境』と（熱という形で）エネルギーの出入りを行いつつ変化している。よってこの『エネルギー』（ヘルムホルツの自由エネルギー）は『系』と『環境』が持っていると考えるべきなのである。
系と環境と、二つのヘルムホルツの自由エネルギーがあるんですか？
いや違う。『系＋環境』という複合系が一つの「ヘルムホルツの自由エネルギー」を持ってます。
環境からエネルギーの補給を受けているとすると、いくらでも仕事できたりしませんか？
それは無理、「補給される」ということ無限に仕事できるということは別だから。実例として、等温環境で気体が膨張するケースを考えると、圧力がどんどん下がってピストンを押す力が弱くなり（やがて外気圧の方が高くなるだろうし）仕事はできなくなる。

断熱された系の平衡状態

　次に、周りとの接触を断って、「熱」（がまだ何なのかは説明していないが）が出入りしないという「断熱された系」を考える。今度は周りとの影響を遮断されているわけだから（たとえば魔法瓶では壁の中に真空を使うことでそれに似た状況を作っている）。

この時の仕事によって変化する量として、さっきのヘルムホルツの自由エネルギーとは別の『エネルギー』を定義することができる。

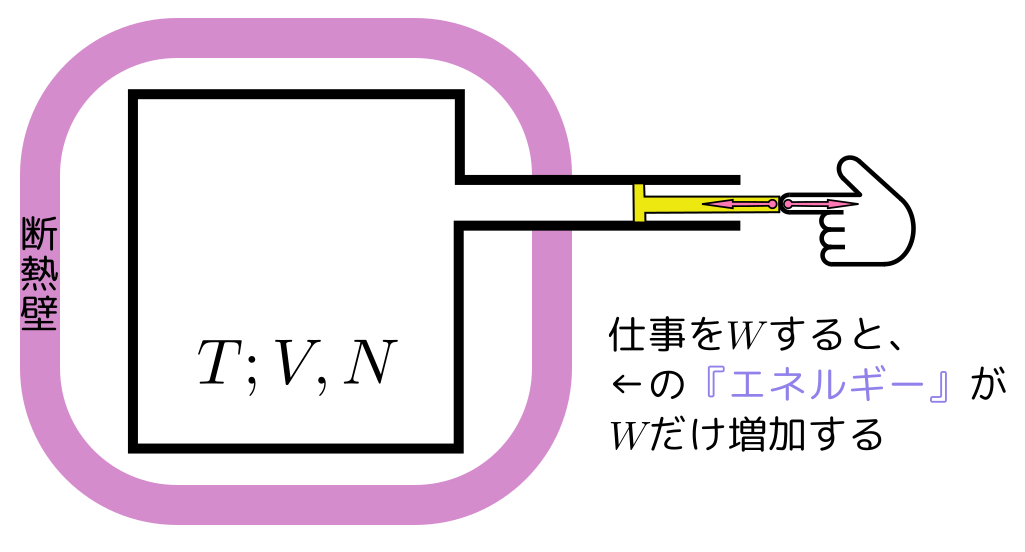
　こっちは内部エネルギーUと呼ばれる。環境と相互作用がないから、内部エネルギーは系が持っていると考えて良い（力学でのエネルギーに近いのはこっちだろう）。

　この場合外界との影響は断っているので、内部の温度Tは環境の温度とは関係ない量である（そして、実際のところ体積を変化させると連動して変化する）。

　今回使っている教科書では「熱」というよくわからない、目に見えないものは後で定義することにして、上で述べたような「操作とそれに対する手応え」で計算できるところの（つまり「目に見えるものから計算できる量」であるところの）「ヘルムホルツの自由エネルギー」や「内部エネルギー」を先に定義していく。

　こうして等温操作と断熱操作を比較してみると、等温操作の時にはTが「環境の温度」であって環境を決めれば決まる変数だったのにたいし、断熱操作では（ピストンを動かすという）操作によってVと連動して変化する変数になっているという違いが見て取れる。よって等温操作ではVと独立な変数であるTは、断熱操作においてはそうならない。

　このように「どの変数が他の変数と独立に動かせるか」が状況によって違うため、熱力学では偏微分計算が多用される。今後の熱力学の計算で偏微分を行う時は、「何を一定とした偏微分を行ったか」に注意する必要がある。