熱力学2015年度第４回

　前回まででヘルムホルツの自由エネルギーの意味をある程度説明したので、今日は教科書３章に従って、用語を定義していきながら進めよう。

等温操作

　まず$(T,X_1)$（温度が$T$で、示量変数の組が$X_1$）で指定される平衡状態があり、そこから等温である環境の中である操作を行い、しばらく待って、$(T,X_2)$（温度が$T$で、示量変数の組が$X_2$）で指定される平衡状態に達した。

　このように等温環境の中で行って、その操作の「出発点（初期状態）」と「到着点（終状態）」が平衡状態になっている操作を「等温操作」と呼ぶことにする。注意すべきは、途中の状態は平衡状態でなくてもよい（平衡状態でない状態は$(T,X)$のように表せないから、途中の状態をこんなふうに記述することもできない）。

このような状態変化を

$(T;X_1){{\rm i}\atop\longrightarrow}(T;X_2)$

と書くことにする。iは等温（isothermal）の頭文字である。

　だから「等温操作」という名前だが操作の途中の温度は一般に$T$ではない（どころか、温度一様ですらない）。

　だから、途中の状態はP-Vグラフとかに描けない。
　「途中の状態は平衡状態じゃない」ということですが、前に書いていたグラフ

では描いてましたが。
あの時の縦軸の圧力は「気体全体の圧力」じゃなくて、「気体のうちピストンに触れている部分」の圧力です。気体全体では圧力が一様じゃない（つまり、Pが１つじゃない）のであの「状態」をP-Vグラフに描き込むことはできないです。

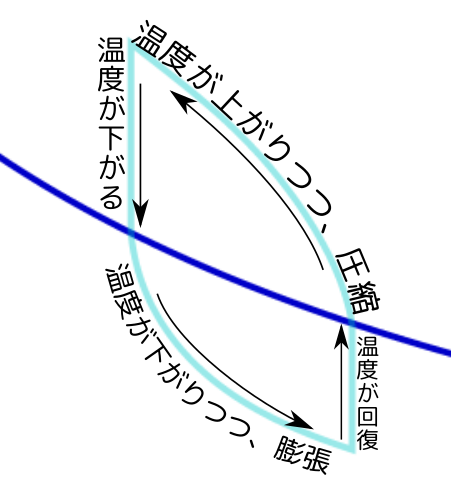
等温準静操作

　等温操作で、かつ途中を準静的に以降させたのが「等温準静的操作」で、この場合途中もすべて平衡状態だから、温度はちゃんと定義でき、かつ常に$T$を保つ。

このような状態変化を

$(T;X_1){{\rm iq}\atop\longrightarrow}(T;X_2)$

と書くことにする。qは準静的（quasistatic）の頭文字である。

　準静的は理想的なもので実現はできないが、これを手がかりにこの後熱力学的現象を考えていくことにする。

　準静的な場合の特徴は「逆が考えられる」ということである。

　準静的でない場合、逆がないということを（極端な）一例で示そう。

　気体をピストンに入れ、急激にピストンを引いたとする。

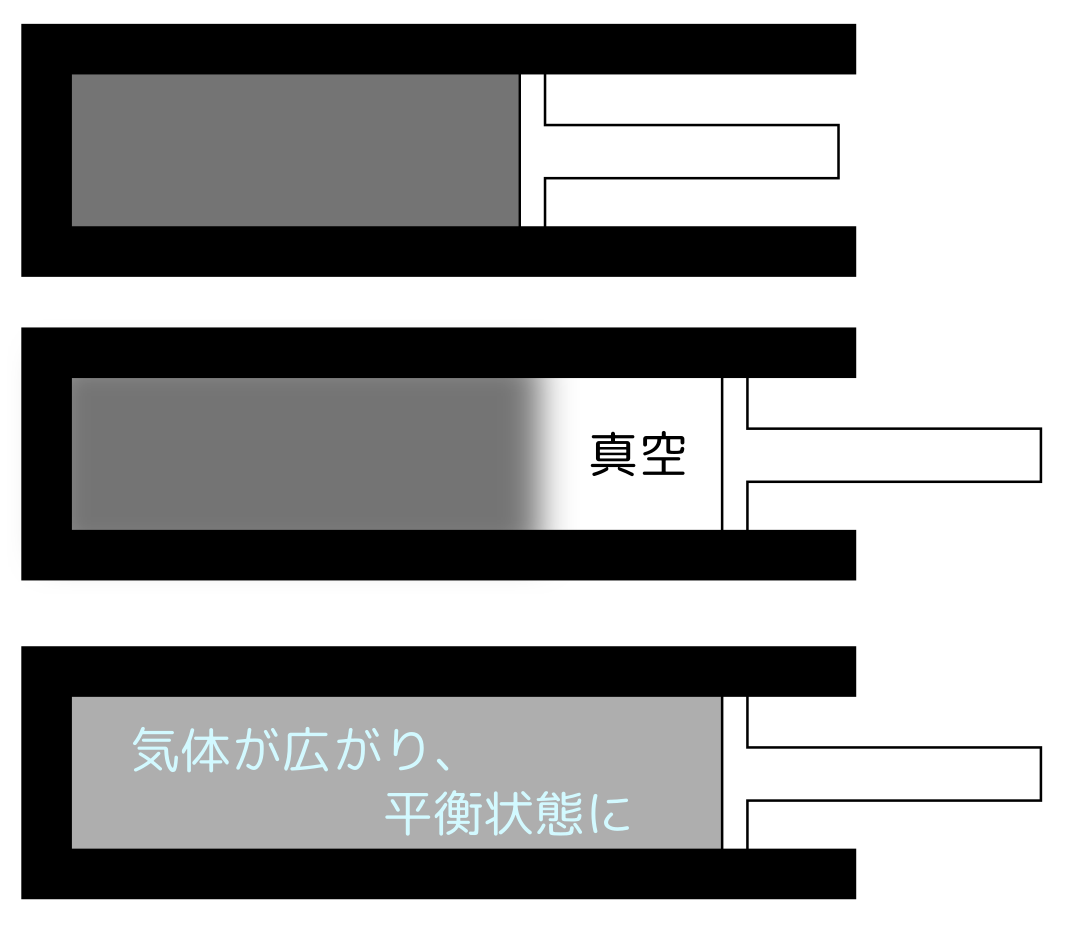
　↑のような変化が起こり（引きが速いのでまず右側に真空ができ、その後気体が全体に拡がっていく）、最後には一様な平衡状態に達する。

　この逆がもしあるとしたら、

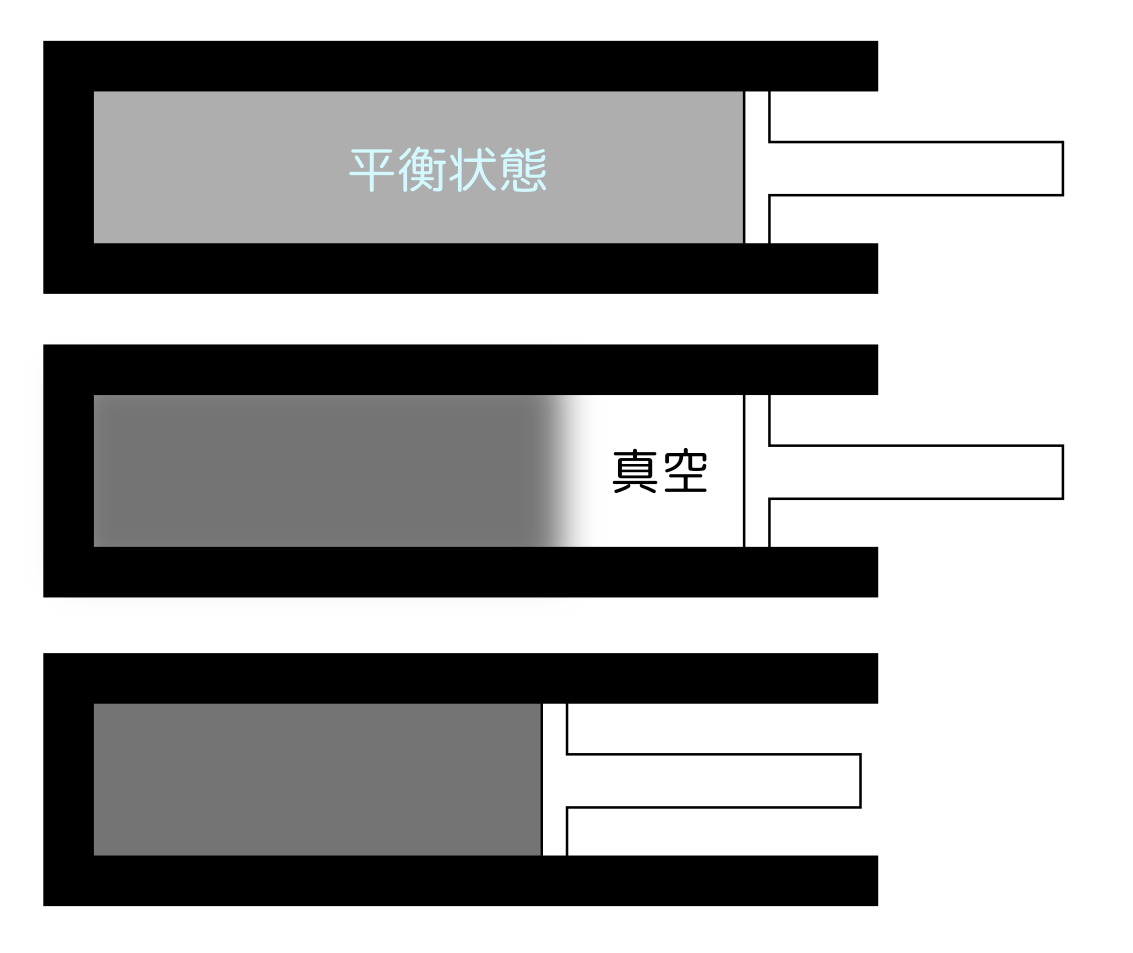
のような現象が起こることになる。つまり、平衡状態にあった気体の右側に突然真空が発生し、その後にピストンが動かされてその真空のところを埋める。

この部屋でもしこんなことが終わったら、右側に座っている人は窒息する。たいへんだ。

　準静的操作では、常に平衡状態を保っているため、逆が可能なのである。

　力学でも熱的現象が起きると逆が考えられなくなる例がある。たとえば放物運動は逆の運動も存在するが、「床に物体が落下して（ドスン、とか音がして）静止した」という現象の逆（静止した物体が周りからの音や振動のエネルギーを吸収して飛び上がる）は起きない。あるいは「摩擦熱が発生して物体が遅くなる」という現象はあるが「周りの温度が下がると物体が加速する」という現象はない。

　これも逆が起こりえるとしたら、安心して道を歩けない。路傍の石が突然飛び上がってきたりしないのも、逆現象がないからである。

　準静的で逆操作を行ったとき、気体のする仕事は「同じ大きさで逆符号」になる（圧力も逆になるから）。

　準静的でない場合、極端な場合を上の例で示したように、膨張する際は気体の出す力が準静的な場合より弱くなり、気体のする仕事は小さくなる。一方収縮する場合は逆に気体が圧縮されることでピストン付近の圧力は局所的に上がるので、力は強くなる。力が強くなるから仕事も大きくなる、と思いきや、収縮する時は運動方向が逆なので仕事は負であり、負の仕事の絶対値が増える、ということはやっぱり「仕事は小さくなる」。

　以上で等温準静操作では「元に戻る」という操作をすると仕事は差し引き0になるが、準静的でない場合は差し引きマイナスになる、ということを気体の例で説明したが、それが一般的にそうだ、というのがKelvinの原理である。

Kelvinの原理

　等温操作で$(T,X)$から$(T,X)$に戻る操作をしたとき、その系のする仕事を$W_{\rm cyc}$とすると、$W_{\rm cyc}\leq0$である。

というのがKelvinの原理。

　上で例に出した気体でなく一般的にそうだ、と主張している。ただしこれは「要請」であって、（少なくとも熱力学の範囲では）何かによって証明されたりはしない。

　こういう「要請」は全ての学問にある。力学なら運動の三法則は証明されないが、「もっともな要請」として受け入れられている。

　Kelvinの原理がある為、自分の状態を変えることなく仕事を生み出す、ということは誰にも（何にも）できない（Kelvinの原理の反例は見つかってない）。これはエネルギー保存則とは別の、新しい法則である。たとえば$W_{\rm cyc}>0$な物が見つかったとしても、エネルギー保存則は満たしている。しかし、Kelvinの原理を満たしてないから存在できない。

　どうして$W_{\rm cyc}>0$でエネルギー保存則を満たせるんですか？？
　今考えているのは等温環境の中に置かれた系なので、周囲と熱のやりとりができます。系が仕事Wをしても、熱Qを吸収して、その吸収した熱Qを仕事にしていると考えれば、エネルギーは保存してます。つまりエネルギーが保存するだけでなく、Kelvinの原理が成り立つという法則も要求しないと、この世界の記述としては不十分になります。

　地球上で、「仕事をし続ける」という現象が起きているときは、なんらかの形でKelvinの原理の前提が成り立っていない。たとえば植物は光合成をしてエネルギーを（ブドウ糖や澱粉を合成するという形で）作り出し続けている。これがなぜ許されるかというと、太陽というエネルギー源であると同時に地球（たとえば25度）よりも高温の状態（太陽の温度は6000度）があって、この温度差による熱の流れをエネルギーに変換できるからである。Kelvinの原理は等温環境の話だから、6000度の物体と25度の物体が共存しているところでは仕事をし続けることができる（その温度差が存在している限りは）。

　要はエネルギーを取り出せるかどうかにとって重要なのは、そこに温度差があるか？ということ。

　たとえば水力発電なんてのも、太陽が水を温めて蒸発させ、雨として高いところに持ち上げてくれるからできる。

　太陽はどこからエネルギーもらうんですか？
　核融合。太陽の水素がヘリウムに変化したりする過程でエネルギーが出てくる。だから何10億年もたつと太陽もエネルギー出せなくなる。

力学におけるポテンシャルエネルギー

　さて、仕事とエネルギーの関係を振り返っておこう。

y

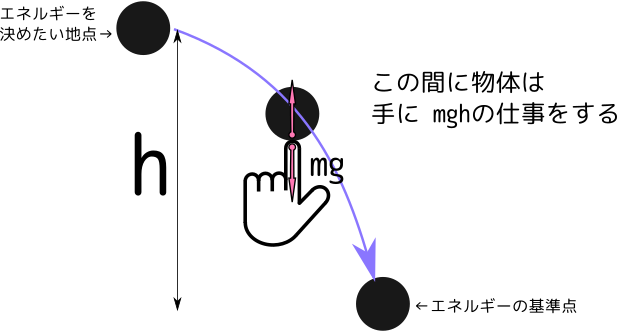
　ポテンシャルエネルギーを決めるには、図のようにまず基準点（ポテンシャルエネルギーが0の点）を決め、エネルギーを求めたい状態から基準点まで物体を移動させた時、物体のする仕事を求める。「物体のエネルギーはした仕事の分だけ減る」というエネルギーの定義から、この時物体のする仕事は最初の場所で持っていたエネルギーそのものになる。

二つのブラックボックス

　熱力学的対象に対して力学の場合と同じように「した仕事の分エネルギーが減る」ということからエネルギーを求めたい。

　我々はブラックボックスの中身を知らなくても、そのブラックボックスを押したり引いたりして仕事をすることで、そのブラックボックスの持つエネルギーを計算することができる。まず（ブラックボックスと言いつつ）よく知っている「フックの法則に従うバネ」の場合で仕事を計算してみる。

大事なのは「ある場所$x$でブラックボックス（実はバネ）の出す力は$kx$である」ということで、これだけ知っていればブラックボックスのする仕事を

$\int_a^b (-kx) \mathrm dx = \left[-{1\over2}kx^2\right]_a^b={1\over2}ka^2-{1\over2}kb^2$

と計算できる（$-kx$にマイナスがついているのは$x$軸負方向の力だから）。

　この仕事はマイナスであるが、その結果として、ブラックボックス（バネ）のエネルギーが${1\over2}ka^2$から${1\over2}kb^2$へと「増えた」と考えられる。つまりバネのエネルギーが${1\over2}kx^2$であることがわかる。

　次にブラックボックスの中にあるのが「等温環境に置かれた理想気体」だとしてみよう。

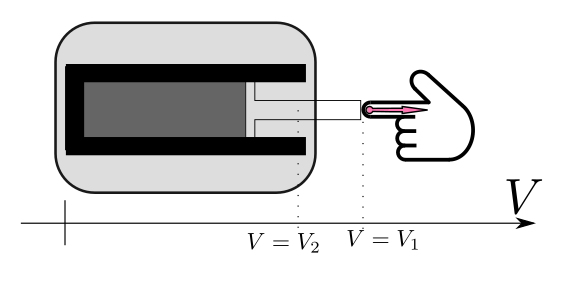
　この時気体のする仕事は

$\int_{V_1}^{V_2} P\mathrm dV$

である。理想気体だとすれば$P={nRT\over V}$であり、等温準静操作だとすれば$T$は定数だから$nRT$を積分の外に出して、

$\int_{V_1}^{V_2} P\mathrm dV=nRT\int_{V_1}^{V_2}{\mathrm dV\over V}=nRT\left[\log V\right]_{V_1}^{V_2}=nRT\log V_2 - nRT \log V_1$

となる。$V_1>V_2$だからこれは負の量である（気体は仕事をされているからこれでよい）。

　この式から気体の持つエネルギーのようなものは$-nRT\log V_1$から$-nRT\log V_2$へと減った、と解釈できる。

　来週、↑の式をもう少し具体的にやる。

　ここで「のようなもの」をつけた理由は二つある。

　一つは「準静的」を仮定したこと（具体的には、$nRT$を「定数」として積分の外に出したところでこの仮定を使った）。よって実際にされる仕事はこれより小さい。

　もう１つは、これは確かに「気体のした仕事」であるが、エネルギーは気体だけが供給していると考えるのはおかしい。等温操作だから気体と環境の間に「熱」という形でエネルギーの移動があるから、ここで変化しているのは「気体＋環境」のエネルギーだと解釈しなくてはいけない。

　このように「仕事」ではなく「最大仕事」をもって定義し、かつ実は計算の仮定で「環境」の持つエネルギーも一緒に計算している「エネルギーのようなもの」が「ヘルムホルツの自由エネルギー」なのである。

最大仕事

　最大仕事は準静的な等温操作で気体のする仕事として定義する。大事なことは通常の「仕事」は過程により違うが「最大仕事」は出発点と到着点だけで決まることである。よって、$W_{\rm max}(T;X_1\to X_2)$のように書く。

ヘルムホルツの自由エネルギー

　力学的エネルギーを決めるとき「基準点」を考えて「その基準点に持っていくまでにできる仕事」でエネルギーを決めた。同様に、「等温操作をしつつある基準点まで変化させるときの最大仕事」で「ヘルムホルツの自由エネルギー」を定義する。

$F[T;X]=W_{\rm max}(T;X\to X_0(T))$

である。ただしこのエネルギーの基準点$X_0(T)$は温度によって変わっていい（まだ基準点は決めない。６章で決める）。

　なぜ「基準点は温度によって変わっていい」ということになるかというと、ここでは「等温操作」でヘルムホルツの自由エネルギーを定義していて、まだ「温度が変わると$F$がどう変わるか」は何にもわからないのである。

ここまでで理解しておくべきことは、温度を１つ決めた時に「最大仕事」を使って$F$が定義（計算）できるということだけである。

　ヘルムホルツの自由エネルギーは、エネルギーが持っているべき条件を満たしている。具体的には、示量的であることと、独立な二つ（示量変数が$X$のものと示量変数が$Y$のもの）がそれぞれ$F(T;X),F(T;Y)$のヘルムホルツの自由エネルギーを持っていたら、合成系のヘルムホルツの自由エネルギーは$F(T;X)+F(T;Y)$になる。

温度が同じじゃなかったらどうなるんですか？
その時は足せない。合成系の温度が一様じゃなくなってしまうから（熱的に接触している場合なら温度が変わってしまうだろうし）。

受講者の感想・コメント

　青字は受講者からの声、赤字は前野よりの返答です。

初めて熱力学がおもしろいと感じた。
お、それは素晴らしい。これからもおもしろさを感じつつ、勉強してください

ねむたすぎてすいまとたたかうのでやっとでした（笑）。
笑っている場合じゃないなぁ。

一般的な等温操作と等温準静操作が異なるという考えは重要である。Kelvinの原理のような要請を考える必要があるというのが、熱力学が実際の物理をうまく表す学問らしいと思った。
現実に合わせて要請を作っていった結果できたのが熱力学です（まぁ、他の物理もだいたいそうなんだけど）。

準静的に操作することは素晴らしいと、講義を聴くたびに思わされます。
そうですね。話をとても楽にしてくれます。

ピストンを押す手がうまく描けないです。GWですがこの講義はなくならないですね、ヤッター。
絵は練習しましょう。また一週間後に。

図解が多くて分かりやすかった。具体的な計算が少しずつ入ってきたので、しっかり復習していきたい。
計算は一度は自分でやってみましょう。

最大の仕事をしても一周させると0になってしまのはとても悲しいなと思いました。
しかしまぁ、しょうがないよね。

Kelvinの原理を学んだ。ヘルムホルツの自由エネルギーが気体だけでなくその周りの環境によるエネルギーであることが分かった。
力学でのエネルギーといろいろ違うので、違いを把握して理解していってください。

Kelvinの原理で、小さいころ永久機関のインテリアが欲しかったことを思い出した。
楽しそうですね、永久機関のインテリア。

Kelvinさんはとても偉大だと改めて思いました。
偉大です（他にもいろいろやってるしね）。

$W_{\rm cyc}$の話がおもしろく感じました。
あれが常に0以下ってのはおもしろいですね。

教科書で少しわかりずらかったヘルムホルツの自由エネルギーがどういったものか、つかめてきた感じがするので、もう一度教科書ノートを読み返してKelvinの原理とともに理解したい。
ヘルムホルツの自由エネルギーのつかめれば、後は楽です。頑張ってください。

光合成の話をしてましたが、もしも地球が太陽と同じ温度であれば、Kelvinの原理により光合成は生じないのですか？
もしすべての場所が等温なら、エネルギーを仕事として取り出す方法はなくなりますね（光合成ももちろんだめ）。

Kelvinの原理がなんとなくわかった。気体って体積を変えてもらうだけでエネルギーをもらえるっていいですね。
「だけ」っていうけど、気体の体積変えるのってたいへんだよ。

Kelvinの原理＆ヘルムホルツの自由エネルギーについて学んだ。ヘルムホルツの自由エネルギーは気体と環境の持つエネルギーだとわかった。
ヘルムホルツの自由エネルギーは大事なので、その概念をしっかり持っていてください。

気体のする仕事を計算すると出た値が気体のエネルギーとは限らないということを系の様子などから導いたのが、なるほどと思った。
気体と環境と、相互作用している相手を全部考えないと、正しい考察にならないですね。

気体のエネルギーのようなもの（$-nRT\log V$）に対する説明がおもしろいと思った。数式で表せるのに様々な条件付けがあるのは、熱力学ならではなのかもしれない。
確かにいろいろな相互作用を考えなくてはいけない分、いろいろややこしいですね。

やっぱりヘルムホルツの自由エネルギーが怖いです。４章５章が終わらないと基準点がわからないなんてとてつもなく怖いです。
エネルギーの基準点というのは普通のエネルギーでもわからない（から適当に決める）ものです。むしろヘルムホルツの自由エネルギーは決め方が他から決まるところが新しい（でもそれは先で理解していきましょう）。

気体と環境のエネルギーを出す時に何も考えずに$nRT$を定数として積分していたが、そのときも準静的であることに気付かされました。ヘルムホルツの自由エネルギーの部分をもう一度理解したいです。
計算のやり方と、今考えている条件設定というのは密接に結びついているものです。

熱力学って、デリケートだと思った。条件も気体も設定してあげる必要がある。都合いいなぁと思ったり。
条件が違うと仕事の仕方も変わるから、エネルギーも定義が変わる、ということがあるので、設定に気を使わなくてはいけないのは仕方ないのです。

ヘルムホルツの自由エネルギーはまわりの環境と関係していて、違う気体どうしをたせるのは等温のときだけとしった。等温でなかったら足すことはできない。
定義の仕方から、等温じゃない系についてヘルムホルツ自由エネルギーを考えてはいけませんね。

ヘルムホルツの自由エネルギーは、名前だけ聞くと難しそうなイメージがあったが、今まで学んだことを考えると理解はしやすかった。
そうです、仕事とエネルギーの定義を素直に拡張すると、等温操作では自然にヘルムホルツの自由エネルギーが出てくるのです。

ヘルムホルツの自由エネルギーは系と周りの環境によるものだということを学べた。
はい、定義と中身を理解していきましょう。

宇宙全体でエネルギーが保存されているのはいいのですが、そのエネルギー自体はどこから来たのでしょう？　ビッグバンから始まったんだとして、爆発が起こる前の物質がどこから来たのか気になりますね。未知のことですか。
ビッグバンというのは「物質が爆発した」わけではなく、それより前には「何も（物質も時空も）なかった」と考えるべきです。というわけでどこから来たも何もない。ビッグバンが全ての「最初」です。

内部エネルギーは示量的でないのかもしれない。GW中にヒマがあれば調べてみます。復習もやります。
内部エネルギーは示量的です。系が変な相互作用をしているとそうはいかない場合もあるでしょうが点…

最大仕事とヘルムホルツの自由エネルギーの関係がよくわからなかった。
う〜ん、そこがわからないと全然分かってないのと同じです。来週でもう一回やりますが、そこはきっちり理解できるようにしましょう。

ヘルムホルツの自由エネルギーを最大仕事という量で定義していて、これからどう発展していくのか楽しみ！　ケルビンさんに圧倒的感謝。
こうして定義した量がいろんな意味を持ってきます。

これからヘルムホルツの自由エネルギーがどう活躍するのか楽しみだ。
お楽しみに。

今回も楽しんで受けることができましたが、後半足早だったので、もう少しゆっくり説明していただければありがたいです。
とりあえず今日のうちに$F$の定義までは話しておきたかったので、ちょっと急ぎました。来週このあたりからもう一回復習しつつ、行きます。

今日はわかったほうだと思う。
それはよかった。

今日やったヘルムホルツの自由エネルギーのところは分かったけど、最後の方はペースが早くてついていくのが大変だった。
とりあえず「ヘルムホルツの自由エネルギーは何か」が分かればオッケー。

授業の最後の方がスピードアップしていったので少しあせりました。
$F$の定義までは喋りたかったので、ちょっと急ぎましたね。