青字は受講者からの声、赤字は前野よりの返答です。
今の講義ではケルビンの原理とヘルムホルツの自由エネルギーの復習をして、等温操作、断熱操作について勉強した。しっかり整理したいと思います。
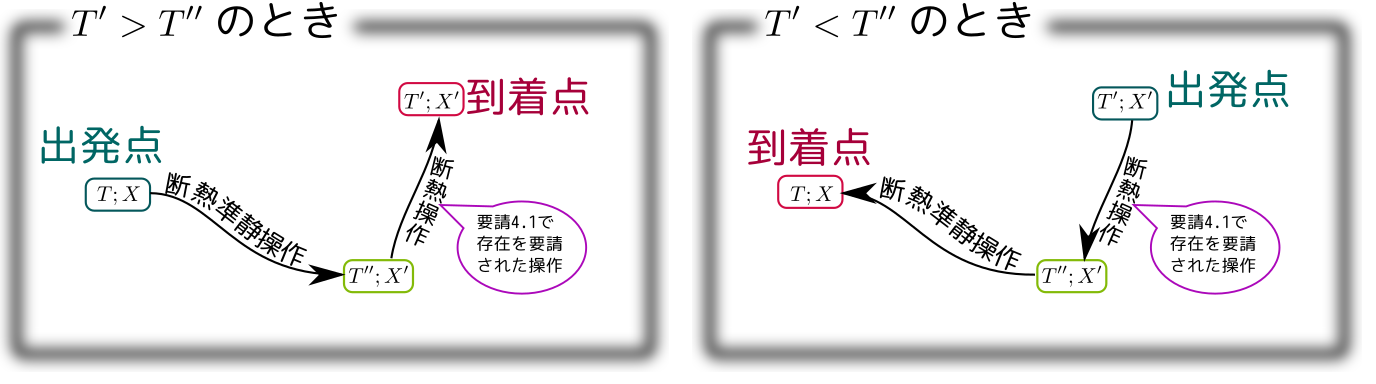
この後、断熱操作と等温操作を組み合わせることでいろんなことを証明していきます。
断熱操作で仕事のさせかたで温度が変わることがわかった。振り子の鳥?? 欲しくなりました。
最近は「ドリンキング・バード」という名前で売ってるようです。
ヘルムホルツの自由エネルギーをきちんと自分の言葉で説明できるようになりたいです。等温操作と断熱操作で混乱してしまったので、復習して理解したいです。
「自分の言葉で説明できる」というのはとても大事なことです。普段から心がけるようにしましょう。
授業の最初でHelmholtzの自由エネルギーの説明をするようにあてられたときに、ポイントを押さえて正確に自分の言葉で説明できなかったので悔しかった。復習の際にノートに自分の言葉でわかりやすい説明を書くように心がけたい。
普段から「ヘルムホルツの自由エネルギーってなんだっけ?」と考えておくようにしましょう。
等温操作と断熱操作で温度$T$が独立であるか従属であるかという違いを認識できるようにしたい。エネルギーの保存も双方では変わってくるのでその辺も注意する。
それぞれの操作の前提を理解して考えるとちゃんと認識できると思います。
水飲み鳥すごいですね。見ていたらいつのまにか終わってました(ノートはちゃんと取りました)。いつまでも見ていたい気がします。
ノートはともかく、話はちゃんと聞きましょう。
断熱操作について学んだ。ふたつの状態があるとき必ずどちらかの方向に変化させる方法があることがわかった。
(準静的な場合を除いて)どちらかしかないというのが面白いところです。
仕事以外のエネルギーの出入りがない中、AができないときはBができる(逆も可)ということがわかった。
どちらかはできることでエネルギーが定義できます。
第一回めの授業で、でてきた内部エネルギーとヘルムホルツの自由エネルギーの違い、二つを区別して考えなければいけない理由がやっとわかった。
この二つの区別が大事なのです。
熱力学の逆が可能でない操作(身体を温めるゴシゴシはあるが冷やすことはできない)におもしろみを感じた。
逆があるとは限らないのが熱力学の面白いところですね。
断熱操作で出た「出発到着が同じならどのような過程でも気体のする仕事は等しい」という理k偽悪の素直なポテンシャルのような考えが、ヘルムホルツの自由エネルギーよりわかりやすかった。
力学に近いのでわかりやすいのですが、それだけでは熱力学にならないのが辛いところ。
等温操作と断熱操作の違いについて学べた。等温なのか断熱なのかに注意して勉強していきます。
この二つの違いが大事です。
ある系の示量変数$X(V,N)$が変化して最大仕事$W_{\rm max}$が得られる時、ヘルムホルツの自由エネルギーが$F=W_{\rm max}$で定義できるということがわかった。断熱操作の時の仕事$W_{\rm ad}$のadは、断熱のadiabaticの頭文字の2文字を取っているということでいいんですか。
はい、adiabaticのadです。
系が周りの環境と仕事以外のエネルギーをするかどうか(等温なのか断熱なのか)を考えヘルムホルツの自由エネルギーと内部エネルギーを区別して考えるということがわかった。
その区別をちゃんとつけながら考えていきましょう。
断熱変化のときの変化の様子を学んだ。
来週、理想気体の場合でどうなるかをやります。
物理の分野は全部つながっていて、ひとつ気になると他のもつながって気になるので質問するより先に自分で調べた方が見につきそうなので、なるべくそうしていきたい。
もちろん自分のペースで自分流にやっていいですが、質問があったらいつでもどうぞ。
断熱操作の時は等温操作の時とは違い準静的に動かしても元に戻らないし、到着点が同じなら。それまでの動きは関係なく仕事が同じだと知った。
いや、準静的なら元に戻りますよ。
独立変数と従属変数の大事さを確認できた。
この先の計算でますます大事になってきます。
内部エネルギーが定義できる話がおもしろかった。
うまいことできてるでしょ。
またしても、あっという間に終わってました。授業とは関係ないのですが、楽しい授業をするコツって何なのか、もしよろしければ教えてください。あ、ちなみに致着ではなく到着ですよ。
楽しい授業をするコツは「自分でストーリーを持って語ること」でしょうか。黒板で漢字間違えてましたか、なんかおかしい気はしてたんだけど。
あんな当たり前の要請から内部エネルギーが定義できたのがとても素晴らしいと思った。熱という量がいかにして導かれるか楽しみです。
熱の導入まではあとちょっとです。割りと、素直な導入です。
断熱操作も加わってきたので、もう一度等温操作のときに満たす条件、断熱操作の条件を整理する。偏微分がこの授業では初めて出てきたので使えるように復習しておく。
熱力学では偏微分は使いまくりますよ。
断熱操作と等温操作、準静的かどうかを意識して考えることが大事だと、今更ながらわかってきました。
どっちも大事なポイントです。
等温と断熱、二つの操作の違いをはっきりさせて、条件などを間違えないようにしたいです。
どうして違いが出てくるか、をじっくり考えてみてください。
内部エネルギーについて復習したい。断熱操作もしっかり勉強しようと思った。
これからこれらの概念を使って先へ進んでいきます。
これから内部エネルギーを習っていく前に、ヘルムホルツの自由エネルギーを理解しておきたいと思います。
両方の定義の仕方と、それからどういう違いが出てくるかを、じっくりと理解しましょう。
前回休んでしまったので少しわからないところがあったので、土日で復習したい。
学問は積み重ねなので、抜けた分のフォローはちゃんとやっておかないと、どんどん遅れますよ。
前回欠席した分の復習が不十分なので、理解できるまで勉強したいと思います。
休んだ分は自分でしっかりやっておきましょう。
等温操作も断熱操作も準静的でなければ元の状態に戻せないことがわかったときに、やっぱり準静的を自然環境で表す?のはとても難しいんだと改めて感じました。
自然を記述するには、ある程度の単純化を行っていかないといけない、ということなのでしょう。
こんがらがりそうだけどよく見ると簡単なことを行っているように見えるので復習して自分の中に落とし込もうと思います。
はい、簡単なんです。自分のまとめ方でまとめてみてください。
授業の最初の先生の質問に答えきれなかったので、しっかり復習してきます。
いろんなことを自分の言葉で説明できるようになることがとても大事です。
なんとなくは理解できた。復習して理解を深めたい。
「なんとなく」から「なるほど」になるまで、頑張ってください。
今日の後半の内容は忘れやすそうなので、何回も復習したいと思います。
これからも出てきますよ、今日の内容は。
断熱操作は等温とは違うところが多いので注意したい。
両方の特徴をよく考えて理解していきましょう。
力学とは異なり不可逆な変化の多い熱力学でのエネルギーの定義の方法が面白かった。
不可逆が入ってくるのが熱力学の面白いところです。
ヘルムホルツと内部エネルギーの違い、等温操作と断熱操作の違いがわかりました。
大事なところです。
断熱の方が外とのエネルギーのやりとりがない分、等温より理解しやすいと思いました。$W_{\rm ad}$=一定の話しがとてもしっくりきました。
断熱と等温、両方とその違いを理解して、勉強を進めていってください。