ここまで示したことと今から示すこと

ここまで示したこと

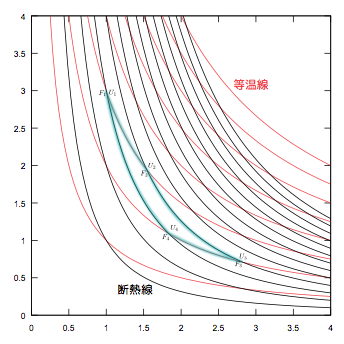
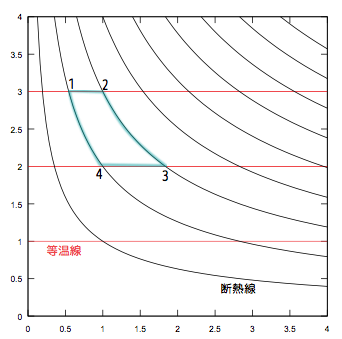
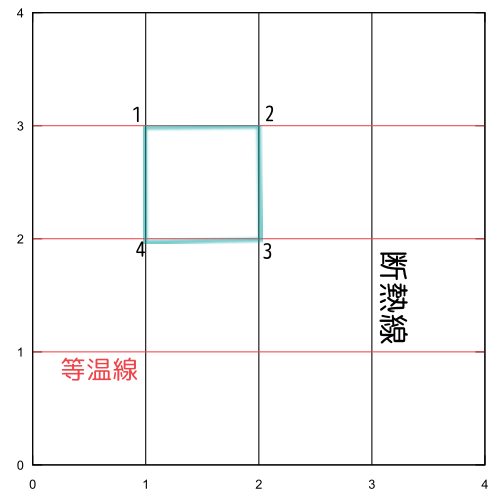
　カルノーサイクルと呼ばれる「等温準静的操作二つと断熱準静的操作二つを組み合わせた系の周期的状態変化」に対し、

${Q_{\rm out}\over Q_{\rm in}}$（ただし、$Q_{\rm in}$と$Q_{\rm out}$は二つの等温準静的操作において系に入ってくる（あるいは系から出て行く）熱量）

を計算する。理想気体の場合ではこの量は${T'\over T}$（$T'$は熱を放出する等温準静的操作での温度、$T$は熱を吸収する準静的操作での温度）になる。

今から示すこと

　実はこの${Q_{\rm out}\over Q_{\rm in}}$は系がどのような物質でできているかによらず同じ値を取ることが証明される（これがCarnotの定理）ので、どのような物質でできた系においても、${Q_{\rm out}\over Q_{\rm in}}={T'\over T}$となる。これを変形した${Q_{\rm out}\over T'}={Q_{\rm in}\over T}$という式は次の章で定義するエントロピーという量と関係していいて、とても重要。

カルノーの定理の一般的証明

　この証明には、

を使う。カルノーサイクルはそのままでは二つの温度（$T,T'$）の熱源と相互作用するサイクルだから、ケルビンの原理の適用範囲外である。そこで、ある意味二つの熱源のうち１つの効果を打ち消すようなことを行う教科書にも記してあるが、以下の証明は少し雑である。気になる人は教科書の付録を読むこと。。

　もう一度カルノーサイクルの図を見よう。

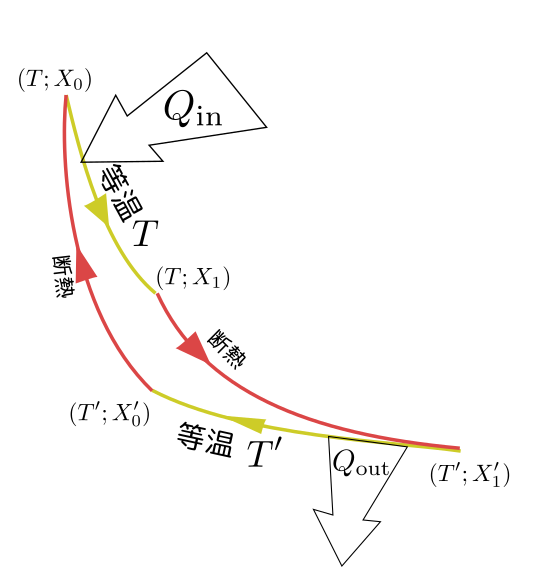
　ここで吸収、放出されている熱は教科書では

$Q_{\rm in}=Q(T;X_0\to X_1)$

$Q_{\rm out}=Q(T';X'_0\to X'_1)$

と書かれている$Q_{\rm out}$の方、図で起こる変化は$X'_1\to X'_0$なのに式では$X'_0\to X'_1$となっていて「逆では？」と思うかもしれないが、この$Q(T';X'_0\to X'_1)$の定義は状態$X'_0$から状態$X'_1$に行くときに吸収する熱量で、$Q_{\rm out}$は放出する熱量という定義なので、二回符号がひっくり返ってこれでよい。。

　もう１つ、逆向きに操作する（元のカルノーサイクルが時計回りなのに対して反時計回りである）「逆カルノーサイクル」を動かそう。

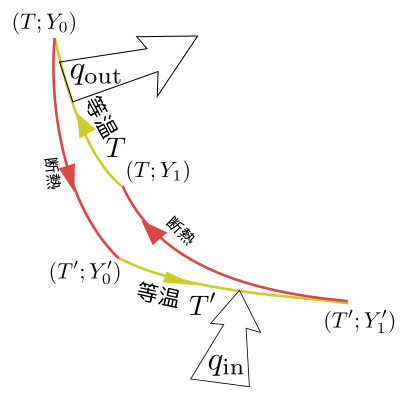
　こちらは吸収、放出する熱は

$q_{\rm in}=Q(T';Y'_0\to Y'_1)$

$q_{\rm out}=Q(T;Y_0\to Y_1)$

となる（逆回転なのでinとoutの位置が違う。また示量変数は$X$ではなく$Y$で表現している）。

　ここでカルノーサイクルが吸収する熱$Q_{\rm in}$と逆カルノーサイクルが放出する熱$q_{\rm out}$が$\alpha$倍違っていたとする（すなわち、$Q_{\rm in}=\alpha q_{\rm out}$）。

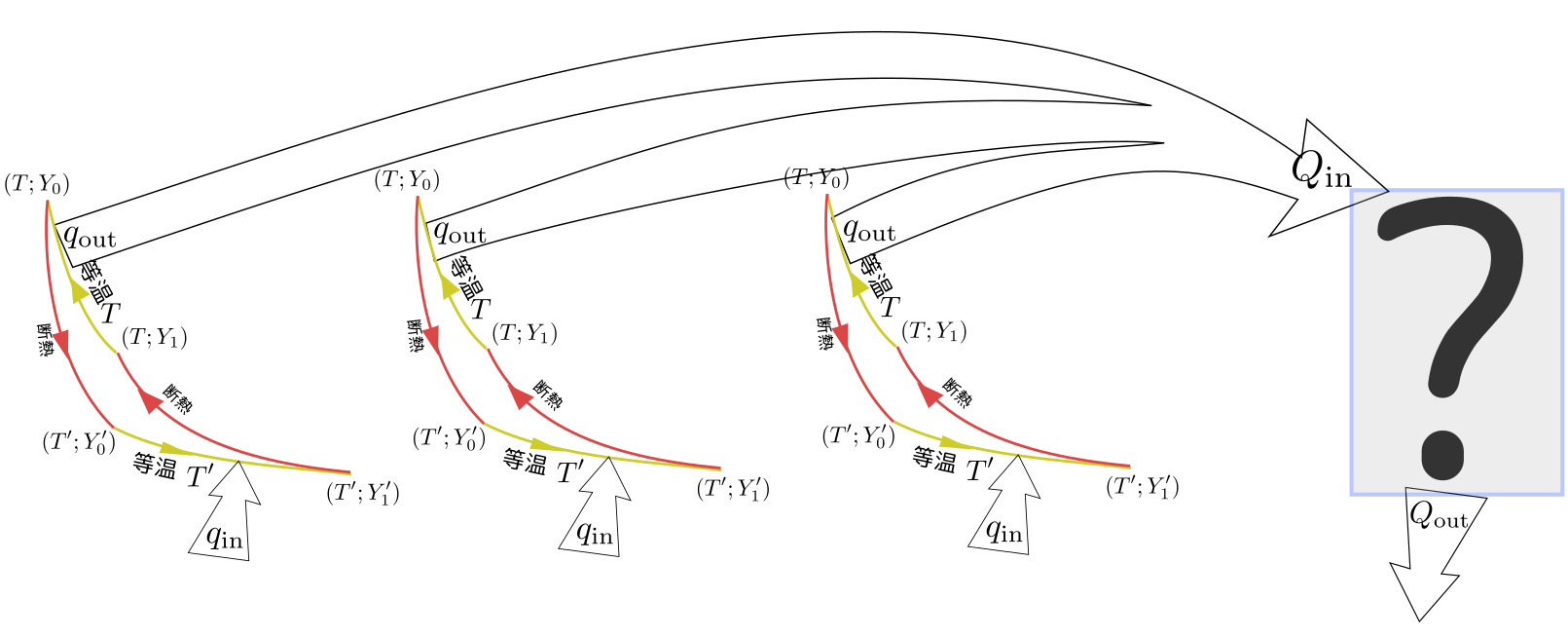
　ここで逆カルノーサイクルを$\alpha$個用意しよう。たとえば$\alpha=3$だとしたら３つのカルノーサイクルを

のように組み合わせ、カルノーサイクルが吸収する熱が逆カルノーサイクル３つが放出する熱と釣り合うようにする。

　このカルノーサイクルの組み合わせが吸収した熱は

$\alpha q_{\rm in}-Q_{\rm out}=\alpha Q(T';Y'_0\to Y'_1)-Q(T';X'_0\to X'_1)$

で、この熱のやりとりは温度$T'$の環境とのみ行われる。

　サイクル運動だから、この式はサイクルのする仕事$W_{\rm cyc}$に等しい。ところがケルビンの原理によりその仕事は0以下であるから、

$\alpha Q(T';Y'_0\to Y'_1)\leq Q(T';X'_0\to X'_1)$

が言える。

　一方、すべてのサイクルを逆回転させると以上の計算のすべてが逆になるから、

$\alpha Q(T';Y'_0\to Y'_1)\geq Q(T';X'_0\to X'_1)$

も言える。結局、

$\alpha Q(T';Y'_0\to Y'_1)=Q(T';X'_0\to X'_1)$

であり、$\alpha$の定義を思い出せば、

${Q_{\rm in}\over q_{\rm out}}\times Q(T';Y'_0\to Y'_1)=Q(T';X'_0\to X'_1)$

すなわち、

${Q(T;X_0\to X_1)\over Q(T';X'_0\to X'_1)}={Q(T;Y_0\to Y_1)\over Q(T';Y'_0\to Y'_1)}$

となって、最大吸熱の比は系が変わっても変わらないことになる。そして、理想気体ではこれが${T'\over T}$であることはすでに見たから、${Q(T;X_0\to X_1)\over Q(T';X'_0\to X'_1)}={T'\over T}$が全ての系に対して言える。

カルノーサイクルではないサイクル

　カルノーサイクル以外のサイクル（以下「謎のサイクル」）の場合でも同様の議論を繰り返して、

のように考えて同様に、

$\alpha q_{\rm in}\leq Q_{\rm out}$

が言える。「謎のサイクル」は逆操作ができるとは限らないから、$\alpha q_{\rm in}\geq Q_{\rm out}$の方は出ない。このことから「謎のサイクル」の吸熱比は等号にならず、

${Q_{\rm out}\over Q_{\rm in}}\geq {Q(T;Y_0\to Y_1)\over Q(T';Y'_0\to Y'_1)}={T'\over T}$

となる。よって「謎のサイクル」の吸熱比は、カルノーサイクルより大きくなる（つまり、熱機関の効率はカルノーサイクルより悪くなる）。

　「謎のサイクル」が「ケルビンの原理」を満たさないような「謎の物質」でできていればこうはならないが、ケルビンの原理を破るような系は見つかってない。誰がが「ぼくの作った最強のサイクル」を持ってきたとしても、ケルビンの原理に反するサイクルを持ってきてない限り、そのサイクルはカルノーサイクルに負ける。