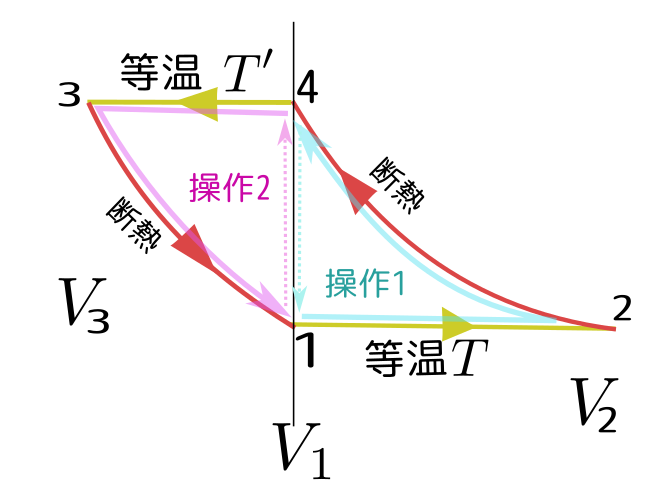
エントロピー導出の流れをもう一度
カルノーサイクルは等温操作と断熱操作を組み合わせているが、その等温線と断熱線を、$V$-$P$グラフ上に表現したものを見てみよう。
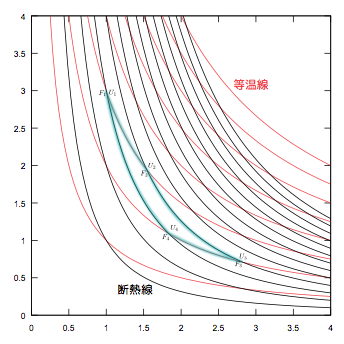
ということに気づいて欲しい。どちらの線も曲線で、しかもよく似ているのだから少々見た目がわかりにくい。そこで縦軸を温度にして、かつ横軸をまだ決めてないある量(エントロピー$S$)にして、経路の図が長方形になるようにできるのでは?---つまり、
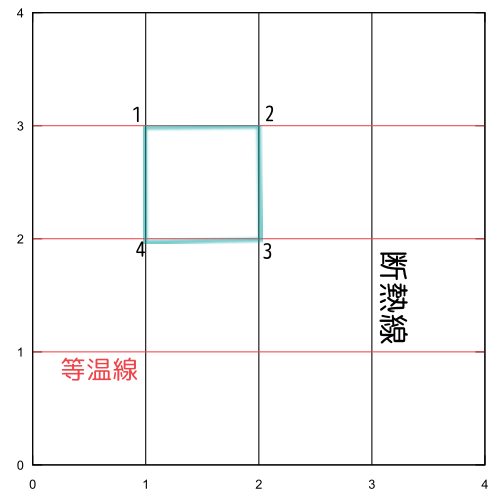
のようなグラフを作りたい!!という「野望」を抱こう。
そのためには$S$はある平衡状態が与えられれば計算できるようにしたいから、「状態量」の組み合わせで作る必要がある。これまで出てきた状態量は、$P,V,T$の他に、
と、
の二つがあった。
$U$と$F$の定義を今の場合に適用すると
等温操作で成り立つ式
- 状態1→状態2で成り立つ式:$F_2-F_1=-W_{{\rm max:}1\to2}$
- 状態3→状態4で成り立つ式:$F_4-F_3=-W_{{\rm max:}3\to4}$
と、
断熱操作で成り立つ式
- 状態1→状態2で成り立つ式:$U_2-U_1=-W_{1\to2}$(←注意:今考えているサイクルとは別の仮想的操作)
- 状態2→状態3で成り立つ式:$U_3-U_2=-W_{2\to3}$
- 状態3→状態4で成り立つ式:$U_4-U_3=-W_{3\to4}$(←注意:今考えているサイクルとは別の仮想的操作)
- 状態4→状態1で成り立つ式:$U_1-U_4=-W_{4\to1}$
が言える。1→2と3→4は等温操作であるが、出発点と到着点が同じになるような断熱操作(あるいは、その逆の操作)は必ず存在していて、その時の仕事で内部エネルギー$U$の差が定義されているので、上のような式を作ることができることに注意。
そして、等温準静的操作での仕事と、同じ出発点・到着点が同じ断熱操作での仕事での差から系の吸収する熱量が定義できているから、
$Q_{\rm in}=U_2-U_1-(F_2-F_1)$(内部エネルギーの増加とヘルムホルツ自由の増加との差が吸熱量)
$Q_{\rm out}=U_3-U_4-(F_3-F_4)$(←こちらは「放出する熱量」なので引き算が逆)
がいえて、かつカルノーの定理${Q_{\rm out}\over Q_{\rm in}}={T'\over T}$または${Q_{\rm out}\over T'}={Q_{\rm in}\over T}$より、
$\displaystyle {U_3-U_4-(F_3-F_4)\over T'}={U_2-U_1-(F_2-F_1)\over T}$
となる。
今から定義する新しい状態量$S$は、断熱準静的操作では変化しないように(つまりカルノーサイクルの$2\to 3$と$4\to1$で変化しないように)しなくてはいけないから、
- 状態2と状態3で変化しない。$S_2=S_3$
- 状態4と状態1で変化しない。$S_1=S_4$
という二つの条件を満たすことが必要となる。この式を辺々引くと
$S_2-S_1=S_3-S_4$
となるが、まずこの式が以下ですぐに示せる。
$\displaystyle {U_3-U_4-(F_3-F_4)\over T'}={U_2-U_1-(F_2-F_1)\over T}$という式をじっくり見ると、$S={U-F\over T}$という量を作ると、この式は
$\displaystyle \underbrace{U_3-F_3\over T'}_{S_3}-\underbrace{U_4-F_4\over T'}_{S_4}=\underbrace{U_2-F_2\over T}_{S_2}-\underbrace{U_1-F_1\over T'}_{S_1}$
となって$S_3-S_4=S_2-S_1$となる。満たして欲しい条件は$S_2=S_3,S_1=S_4$だから、この二つの式の引き算については証明できた。
さて問題は$S_2=S_3$になるかどうかだが、その式は
$\displaystyle {U_2-F_2\over T}={U_3-F_3\over T'}$
である。ここで$F$の定義が、
だったことを思い出す。この定義は、等温操作による変化である$1\to2$と$3\to4$においてどのように$F$が変化したかは定義されている(つまり$F_2-F_1$と$F_4-F_3$は決っている。しかし$F_2$と$F_3$の関係については何も言ってない(決めてない)。
別の言い方をすれば、$F$は一本の「等温線」の上では値が(正確には、等温線に沿って動くときにどう値が変化するか)は決っているが、違う等温線ではどう変化するか(たとえば、断熱線に沿って動いたときにはどう変化するのか??)は「まだ」決めていない。
「じゃあいつ決めるの?---今でしょ!」ということでここで、$S_2=S_3$になるように決める。
$S_3-S_4=S_2-S_1$はすでに示したから、$S_2=S_3$ならば$S_4=S_1$も決まる。
このようにして決めた新しい状態量が$S$すなわちエントロピーである。