図形の変換を表す「行列」
次に、平面の図形を変換ここで行うのは線形変換もしくは1次変換と呼ばれる変換のみ。する手段としての「行列」を見よう。というより、「行列で表現できるような変換の組」をここでは扱う。
元の図を、以下のような「シュレーディンガーの猫」の絵としよう。
元の図: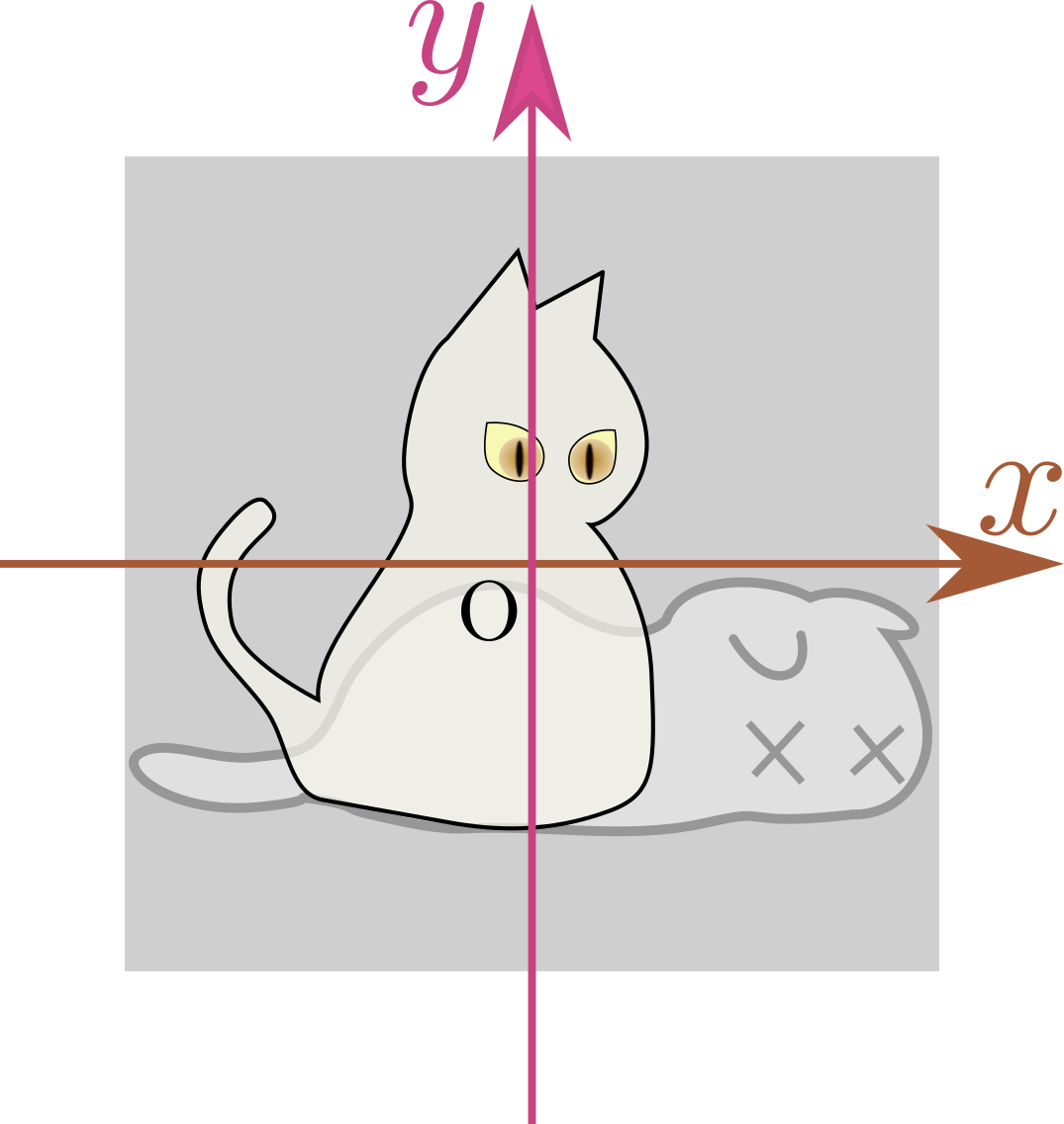
この図の変形として、以下のようなものを考える。まずはシンプルな「反転」である。2種類ある。
左右反転:$\mtx[c]{\xcol{x}\\\ycol{y}}\to\mtx[c]{-\xcol{x}\\\ycol{y}}$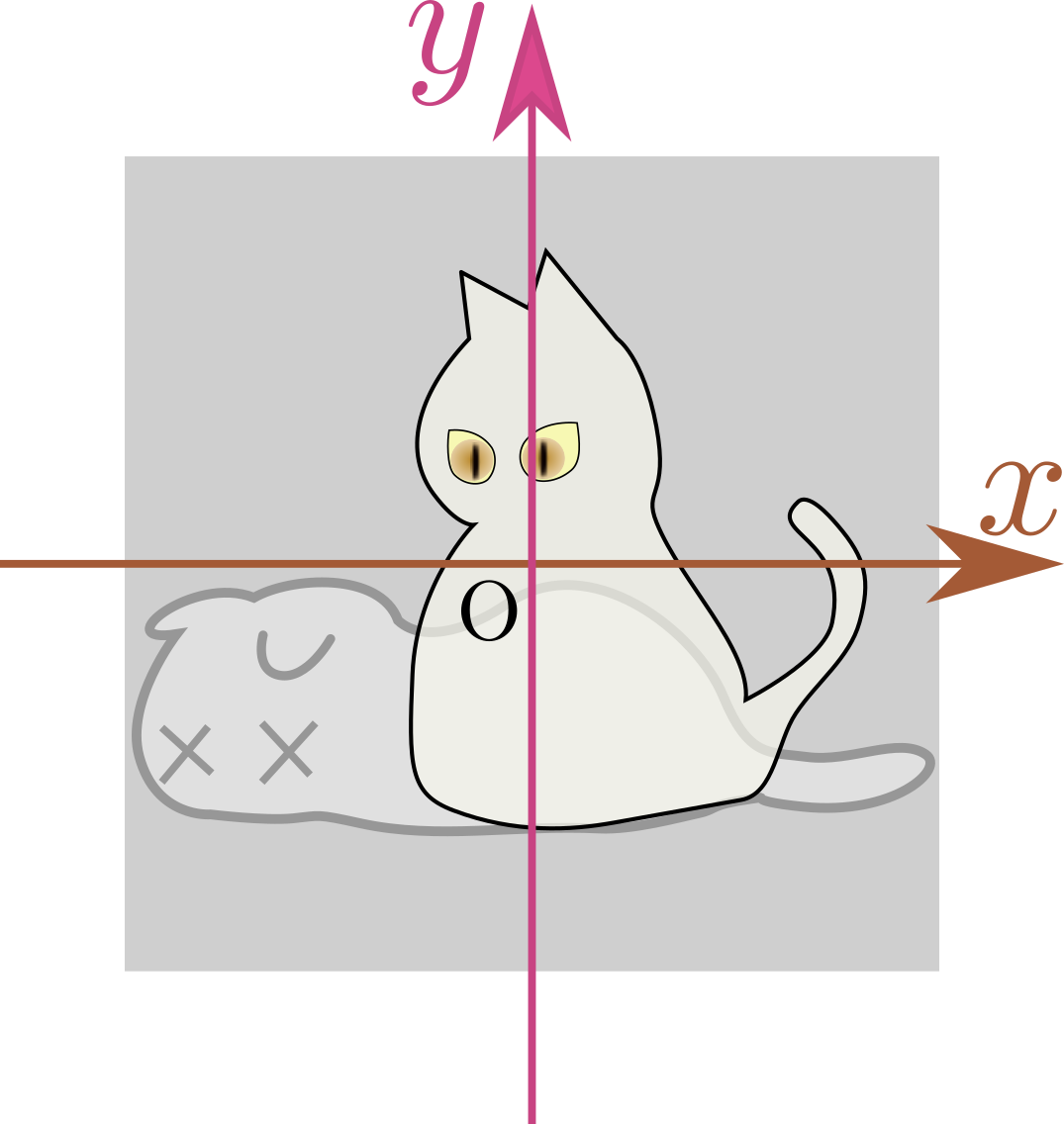
上下反転:$\mtx[c]{\xcol{x}\\\ycol{y}}\to\mtx[c]{\xcol{x}\\-\ycol{y}}$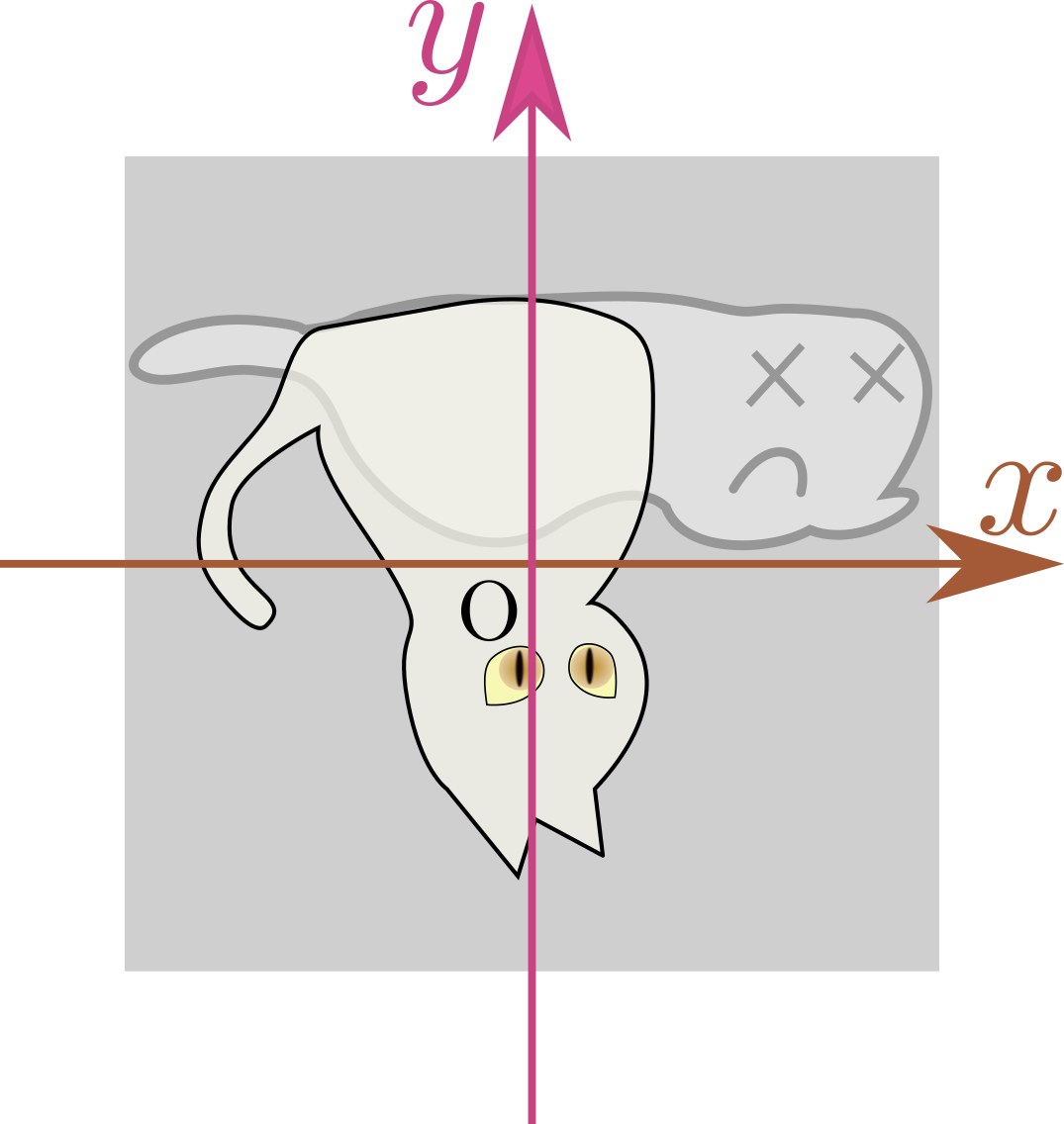
この「反転」は平面上の$\xcol{x}$座標または$\ycol{y}$座標の符号をひっくり返すという操作だが、それは画像を鏡像反転させる操作になっている。
次に「伸縮」の2種類を考えよう。
左右伸縮:$\mtx[c]{\xcol{x}\\\ycol{y}}\to\mtx[c]{\alpha\xcol{x}\\\ycol{y}}$
上下伸縮:$\mtx[c]{\xcol{x}\\\ycol{y}}\to\mtx[c]{\xcol{x}\\\alpha\ycol{y}}$ 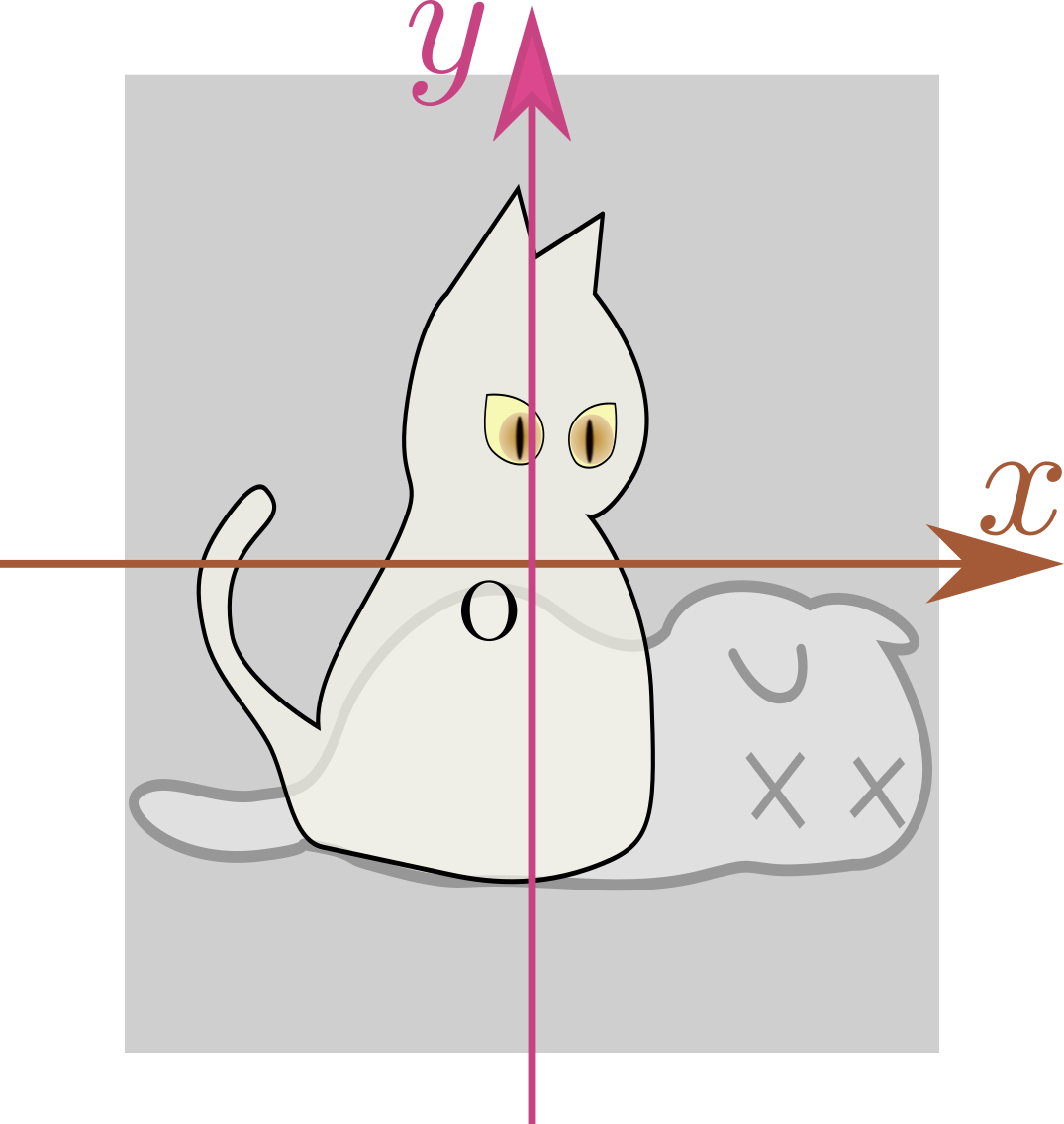
さらに、「回す」ということが考えられるだろう。この式は少しだけ難しい(この章はイントロなので、この式については後でゆっくりやることにする)。
回転:$\mtx[c]{\xcol{x}\\\ycol{y}}\to\mtx[c]{\xcol{x}\cos \theta-\ycol{y}\sin\theta\\\xcol{x}\sin\theta+\ycol{y}\cos\theta}$
ここまでは形を(反転はしても)変えない変換だったが、以下の操作では形が歪みを生じる。
垂直ずらし:$\mtx[c]{\xcol{x}\\\ycol{y}}\to\mtx[c]{\xcol{x}\\\ycol{y}+\alpha\xcol{x}}$ 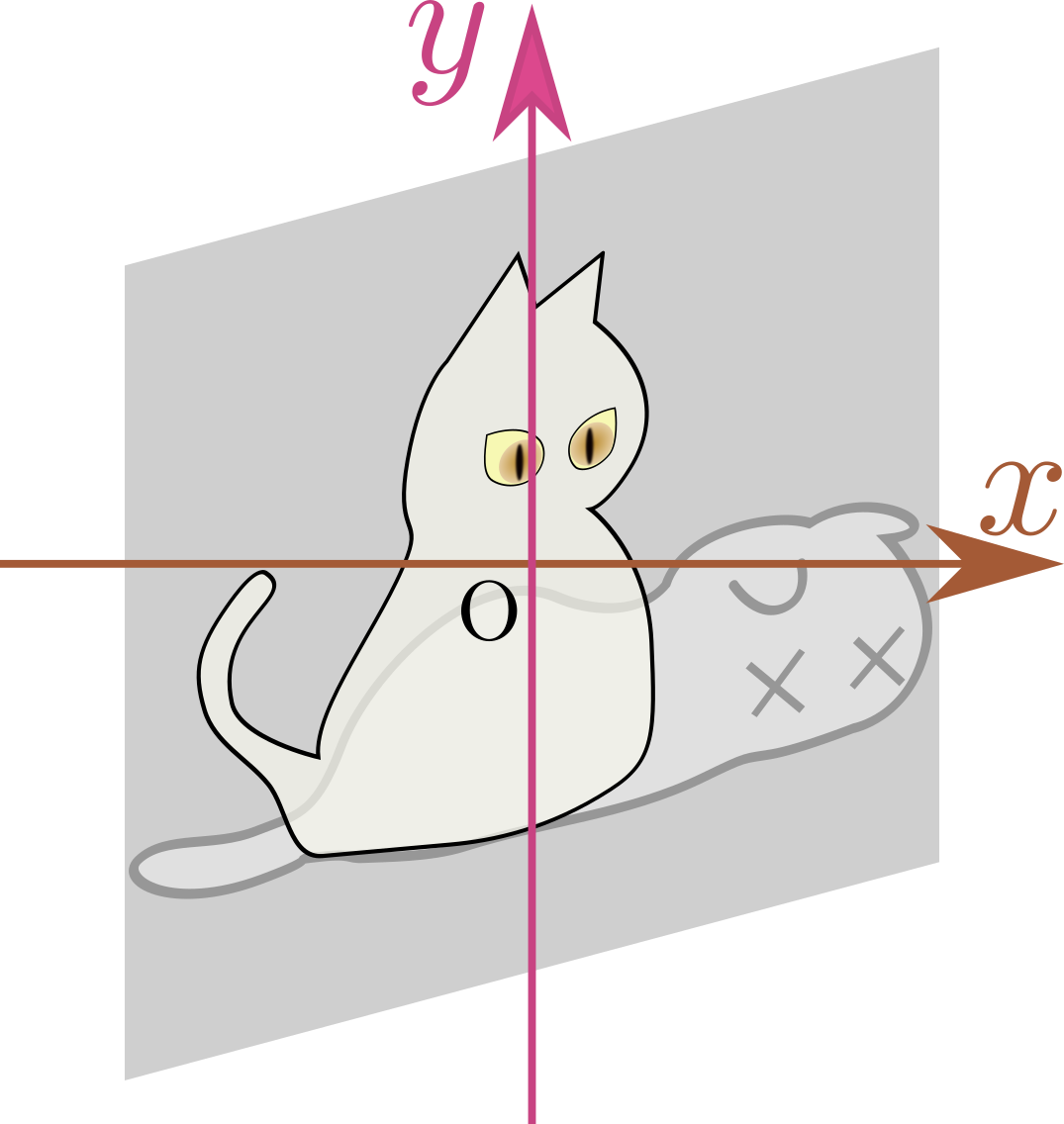
水平ずらし:$\mtx[c]{\xcol{x}\\\ycol{y}}\to\mtx[c]{\xcol{x}+\alpha\ycol{y}\\\ycol{y}}$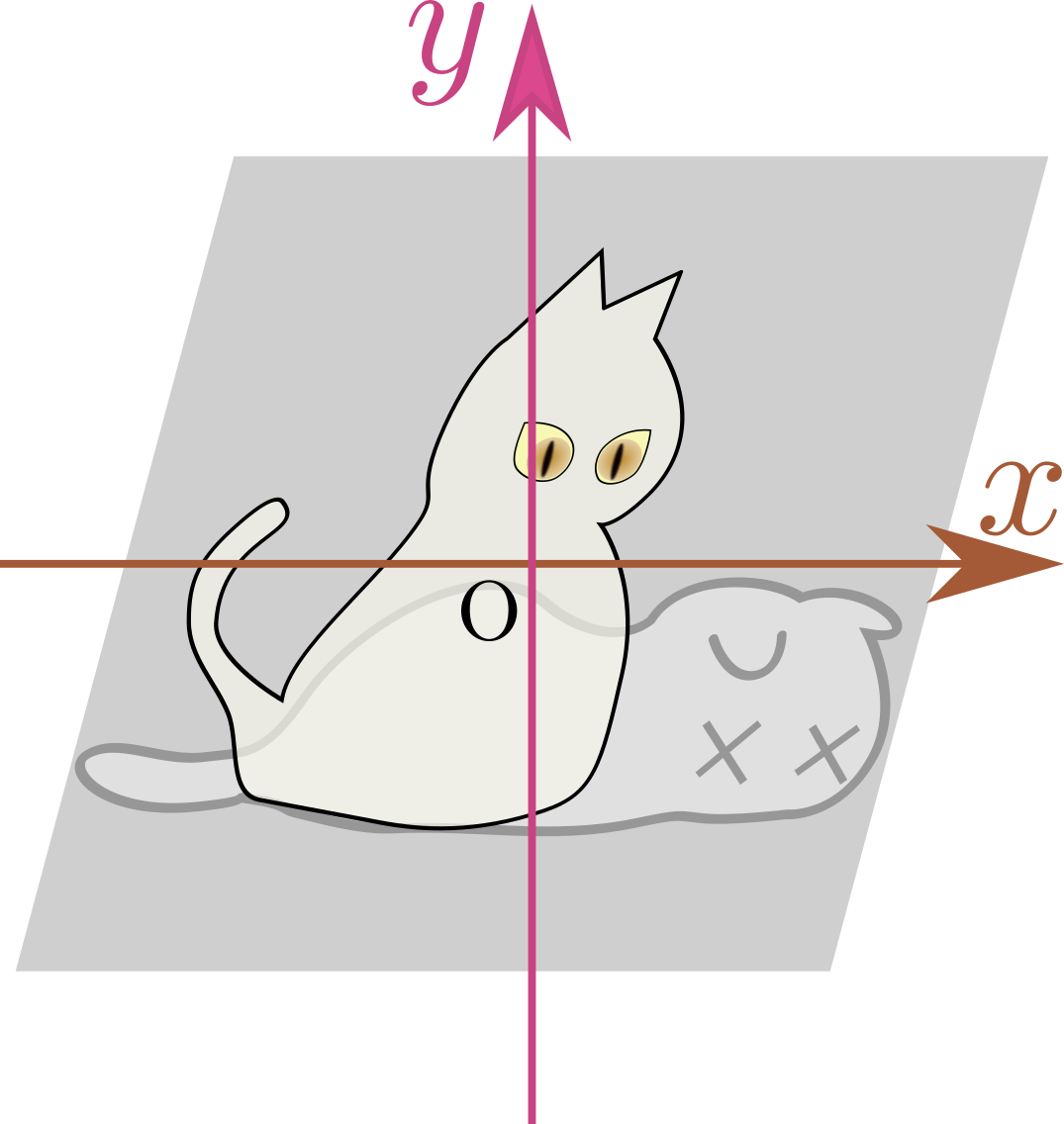
$a=-1,b=0,c=0,d=1$と選べば左右反転が表現できる。
ここで、 \begin{align} \mtx[cc]{a&b\\c&d}\mtx[c]{\xcol{x}\\\ycol{y}}=\mtx[c]{a\xcol{x}+b\ycol{y}\\c\xcol{x}+d\ycol{y}} \end{align} のように「行列の計算ルール」を定めておくと、行列$ \mtx[cc]{a&b\\c&d}$を一つ決めることで以上の変換がすべて表現できることになる。たとえば、左右反転の行列は$\mtx{-1&0\\0&1}$で、これによって \begin{align} \mtx[cc]{-1&0\\0&1}\mtx[c]{\xcol{x}\\\ycol{y}}=\mtx[c]{-\xcol{x}\\\ycol{y}} \end{align} のような計算がされる。
操作と、行列の関係を整理すると以下のような感じだ。
| 左右反転 | 上下反転 | 左右伸縮 | 上下伸縮 | 回転 | 垂直ずらし | 水平ずらし |
| $\mtx{-1&0\\0&1}$ | $\mtx{1&0\\0&-1}$ | $\mtx{\alpha&0\\0&1}$ | $\mtx{1&0\\0&\alpha}$ | $\mtx{\cos \theta&-\sin \theta\\\sin \theta&\cos \theta}$ | $\mtx{1&0\\\alpha&1}$ | $\mtx{1&\alpha\\0&1}$ |
こうやってできあがった行列の表現を見ると、$\alpha=-1$の左右伸縮は左右反転であることがわかる(同様に$\alpha=-1$の上下伸縮は上下反転である)。さらに言えば反転と収縮は全部まとめて$\mtx{\alpha&0\\0&\beta}$という行列で表現できる。
行列で書いたことのメリットはやはり、「操作をまとめることができる」ということである。たとえば

という操作は行列では \begin{align} \mtx{\cos \theta&-\sin \theta\\\cos \theta&\sin \theta} \mtx{1&0\\\alpha&1}\mtx[c]{\xcol{x}\\ \ycol{y}} =& \mtx{\cos \theta&-\sin \theta\\\sin \theta&\cos \theta} \mtx[c]{\xcol{x}\\ \ycol{y}+\alpha\xcol{x}} \nonumber\\ =& \mtx[c]{ \xcol{x}(\cos \theta-\alpha\sin \theta) -\ycol{y}\sin \theta \\ \xcol{x}(\sin \theta+\alpha\cos \theta) +\ycol{y}\cos \theta} \end{align}
と表現できる。
ここで大事なことを一つ。上とは操作の順番を変えた

角度$\theta$回してから$\alpha$の垂直ずらしをする
という操作の結果は、見てわかるとおり、全く違う(操作の「部品」は同じでも、順番が変われば結果が変わる)。
このことは行列の計算にも当然反映されていて、行列の順番を変えたときの結果 \begin{align} \mtx{1&0\\\alpha&1} \mtx{\cos \theta&-\sin \theta\\\sin \theta&\cos \theta}\mtx[c]{\xcol{x}\\\ycol{y}} =& \mtx{1&0\\\alpha&1} \mtx[c]{\xcol{x}\cos \theta-\ycol{y}\sin \theta\\\xcol{x}\sin \theta+\ycol{y}\cos \theta} \nonumber\\ =&\mtx[c]{\xcol{x}\cos \theta-\ycol{y}\sin \theta\\\xcol{x}(\sin \theta+\alpha\cos \theta)+\ycol{y}(\cos\theta-\alpha\sin \theta)} \end{align} となって、全く違う変換となる。
で実際に試しながら確認して欲しい。今日のwebClassでこれに関する問題を出す。
行列を使うメリット
ここまでだと、行列で書いたって大して変わらんじゃないか、という感想を抱くかもしれない。行列で書いたことの意義は何かというと、 \begin{equation} \gunderbrace{ \mtx{a&b\\c&d}}_{操作} \gunderbrace{\rv{\xcol{x}\\ \ycol{y}}}_{入力} =\gunderbrace{\rv{\zcol{X}\\\thetacol{Y}}}_{出力} \end{equation} のように、式の上で「入力」「操作」「出力」が分離されてくるということにある。
「操作」が分離されているおかげで、上の計算を \begin{equation} \gunderbrace{ \mtx{a&b\\c&d}}_{操作} \rv{\xcol{x}\\ \ycol{y}} =\rv{X\\Y} ~~\to~~ \rv{\xcol{x}\\ \ycol{y}} =\gunderbrace{{1\over D}\mtx{d&-b\\-c&a}}_{逆操作}\rv{X\\Y}\label{gyakusousa} \end{equation} (ただし、$D=ad-bc$のように「逆操作」を作るという演算だとか考えることができるのである。具体的にどのようにこの逆操作を考えていくかについては後でじっくり説明する。
また、二つの操作を続けて行なうとき---たとえば、まず$\mtx{e&f\\g&h}$で表される操作を行ったのち、$\mtx{a&b\\c&d}$で表される操作を行う(上でやった「ずらした後で回転する」など)のであれば、 \begin{equation} \gunderbrace{ \mtx{a&b\\c&d}}_{第2の操作} \gunderbrace{ \mtx{e&f\\g&h}}_{第1の操作} \rv{\xcol{x}\\ \ycol{y}}\label{twosousa} \end{equation} となる(第1の操作を行った結果に第2の操作を行っている)。
ここで、第1の操作と第2の操作をまとめて行なうという操作を、一つの行列で表現してしまうことができる、というのが行列を使うことの強みの一つである。同じことを行列を使わない計算で書くと、 \begin{equation} \goverbrace{\begin{cases} \xcol{x'}=e\xcol{x}+f\ycol{y}\\ \ycol{y'}=g\xcol{x}+h\ycol{y} \end{cases}}^{第1の操作}~~~~ \goverbrace{ \begin{cases} \xcol{x''}=a\xcol{x'}+b\ycol{y'}\\ \ycol{y''}=c\xcol{x'}+d\ycol{y'} \end{cases}}^{第2の操作}\label{daiichidaini} \end{equation} をまとめて、 \begin{equation} \begin{cases} \xcol{x''}=a\goverbrace{(e\xcol{x}+f\ycol{y})}^{\xcol{x'}}+b\goverbrace{(g\xcol{x}+h\ycol{y})}^{\ycol{y'}}=(ae+bg)\xcol{x}+(af+bh)\ycol{y}\\ \ycol{y''}=c\goverbrace{(e\xcol{x}+f\ycol{y})}^{\xcol{x'}}+d\goverbrace{(g\xcol{x}+h\ycol{y})}^{\ycol{y'}}=(ce+dg)\xcol{x}+(cf+dh)\ycol{y} \end{cases}\label{matomete} \end{equation} となる。ごちゃごちゃしてわかりにくい。
これを再び行列の言葉に翻訳しよう。 \begin{equation} \goverbrace{\mtx[c]{\xcol{x''}\\\ycol{y''}} =\mtx{a&b\\c&d}\mtx[c]{\xcol{x'}\\\ycol{y'}}}^{第1の操作}~~~~~~~~ \goverbrace{ \mtx[c]{\xcol{x'}\\\ycol{y'}}=\mtx{e&f\\g&h}\mtx[c]{\xcol{x}\\\ycol{y}}}^{第2の操作} \end{equation} と翻訳され、もうひとつの式は \begin{equation} \mtx[c]{\xcol{x''}\\\ycol{y''}} = \goverbrace{\mtx{a&b\\c&d}}^{第2の操作} \goverbrace{\mtx{e&f\\g&h}}^{第1の操作}\mtx[c]{\xcol{x}\\\ycol{y}} =\goverbrace{\mtx{ae+bg&af+bh\\ce+dg&cf+dh}}^{二つの操作をまとめた表現}\mtx[c]{\xcol{x}\\\ycol{y}} \end{equation}
のように翻訳される(ここの説明も、後でじっくりやるから今は「ふむふむ、後でそんな計算をやるのね…」程度に思いながら眺めておけばよい)。
ここで行列を使ったことの強みが現れる。というのは、この場合、 \begin{equation} \mtx{a&b\\c&d} \mtx{e&f\\g&h} =\mtx{ae+bg&af+bh\\ce+dg&cf+dh} \end{equation} という計算を先にやってしまうことができるのであるこれができるのは行列やベクトルの掛け算において「結合法則(後述 )」が成り立つから。。
このように操作を行列という形でまとめることには、単純に見栄えの問題ではないメリットがある。たとえば我々は \begin{align} \opcol{\diff \over \kidt}x\kakko{t}=&A_{xx}\,x\kakko{t}+A_{xy}\,y\kakko{t} \\ \opcol{\diff \over \kidt}y\kakko{t}=&A_{yx}\,x\kakko{t}+A_{yy}\,y\kakko{t} \end{align} のような「連立微分方程式」を解かなくてはいけないこともあるが、これを \begin{align} \opcol{\diff \over \kidt}\mtx[c]{x\kakko{t}\\ y\kakko{t}}=\mtx{A_{xx}&A_{xy}\\A_{yx}&A_{yy}}\mtx[c]{x\kakko{t}\\ y\kakko{t}} \end{align} と書いておくと、微分方程式を解く手間が大幅に減る(1変数の方程式を2回解く程度の手間で済む)。これについても、後でじっくり述べよう。
この章は本当に「イントロ」なので複雑な話を全くしてない。なので「こんな簡単なことなら別に行列とか新しいもの使わなくてもいいのでは?」と思ってしまう人もいるかもしれない。だが、行列を使って線形代数を考えることで、間違いなく世界は広がる。物理はもちろんAIなどの応用も含め、工学や経済学なども含めた広い範囲で線形代数は応用されているのである。来週からは、その基礎の部分を学んでいこう。
最初に、今日やった「行列による図形の変換」に関する問題が一問あります。
- (a)「伸縮」と「伸縮」
- (b)「伸縮」と「回転」
- (c)「伸縮」と「ずらし」
- (d)「回転」と「回転」
- (e)「回転」と「ずらし」
- (f)「ずらし」と「ずらし」
この問題への解答が正解かどうかは、成績には影響しません。
あと、授業への感想・コメントと、オンライン授業についての要望などを書く欄がありますので、そちらも記入してください。
物理数学I webclass
この感想・コメントシートに書かれたことについては、代表的なものに対しては次のページで返答します。
なお、webClassに情報を載せていますが、授業があった日の午後7時より約1時間、オンラインオフィスアワーとしてzoomを開いてます。質問や相談などがある人は来て話してください。