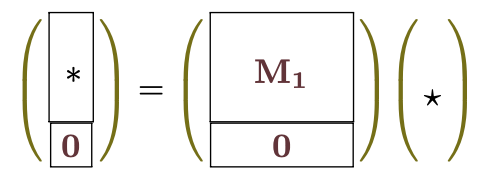前回の感想・コメントシートから
前回の授業の「感想・コメント」の欄に書かれたことと、それに対する返答は、
にありますので見ておいてください。
前回は「回転」という具体例についてですが、今回で少し抽象的な一般論をやります。
ベクトル空間
ここまで、ベクトルを「数を並べたもの」とか「矢印」とか、具体的なものとして扱ってきた。数学の利点の一つは「抽象化」である(抽象化することによって問題をより広い視点で見ることができるようになる)。
そこで、以下では「ベクトル」という言葉の意味をずっと広く取ることにする。
以下の話の説明ビデオは↓
まず大雑把に述べておくと足し算とスカラー倍ができるようなものは全部ベクトルである。
そんなことを言ったらたいていの量はベクトルでは?と思った人へ---あなたは正しい。
ベクトル空間の条件
以下では、「ベクトル」という言葉を非常に抽象的に使うので、その意味でのベクトルはこれまでの$\vec a$のように矢印を使うのではなく、$\avec{a}$のように色付きゴシック体で表現することにする。その抽象的な「ベクトル」の集合が「ベクトル空間」である。
以下のような性質を持つ集合を「ベクトル空間」と呼ぶ。
ベクトル空間の条件:加法
次のような性質を持つ「加法」と呼ぶ二つの元から一つの元への写像$\left\{\avec{a},\avec{b}\right\}\mapsto\avec{a}+\avec{b}$が定義できる。
- 交換則 任意の元$\avec{a}$について、
\begin{equation}
\avec{a}+\avec{b}=\avec{b}+\avec{a}
\end{equation}
- 結合則 任意の元$\avec{a},\avec{b},\avec{c}$について、
\begin{equation}
(\avec{a}+\avec{b})+\avec{c}=\avec{a}+(\avec{b}+\avec{c})
\end{equation}
- 単位元 任意の元$\avec{a}$について、
\begin{equation}
\avec{a}+\avec{0}=\avec{a}
\end{equation}
となる元(単位元と呼び「$\avec{0}$」と書く)が存在する。
- 逆元 任意の元$\avec{a}$について、
\begin{equation}
\avec{a}+(-\avec{a})=0
\end{equation}
となる元$-\avec{a}$が存在する。
「加法」は、より精密に書くなら、ベクトル空間の要素の任意の組$\avec{a},\avec{b}$に対してベクトル空間の要素が一つ対応するという対応関係を作ることができる、ということになる。名前は「加法」であるが、この性質を持っていれば実際の演算はどんなものでもいい。
ベクトル空間の条件:スカラー倍
次のような性質を持つ「スカラー倍」$\avec{a}\mapsto\alpha\avec{a}$が定義できる。
- 可換性 任意の元$\avec{a}$とスカラー$\alpha,\beta$について、
\begin{equation}
\alpha(\beta \avec{a})=\beta(\alpha \avec{a})
\end{equation}
- 1倍 任意の元$\avec{a}$について、
\begin{equation}
1\times \avec{a}=\avec{a}
\end{equation}
- 分配則(ベクトルの和について) 任意の元$\avec{a},\avec{b}$とスカラー$\alpha$について、
\begin{equation}
\alpha(\avec{a}+\avec{b})=\alpha\avec{a}+\alpha\avec{b}
\end{equation}
- 分配則(スカラーについて)
任意の元$\avec{a}$とスカラー$\alpha,\beta$について、
\begin{equation}
(\alpha+\beta) \avec{a}=\alpha \avec{a}+\beta\avec{a}
\end{equation}
こちらもより精密に書くなら、ベクトル空間の要素の任意$\avec{a}$とスカラー(実数または複素数)$\alpha$の組に対してベクトル空間の要素が一つ対応するという対応関係を作ることができる、ということになる。
以上が、その集合が「ベクトル空間(vector space)」(または「線形空間(linear space)」)であるための必要条件である。上の定義の中で用いた「スカラー」が実数である場合を「実ベクトル空間(real vector space)」(または「実線形空間(real linear space)」)、複素数である場合を「複素ベクトル空間(complex vector space)」(または「複素線形空間(complex linear space)」)と言う。実ベクトル空間と複素ベクトル空間はそれぞれ「実数を係数体とするベクトル空間」「複素数を係数体とするベクトル空間」のように呼ぶこともある。
FAQ:この「定義」はベクトルの性質でやったのと同じものでは?
同じものを含んでいるが、前に考えたときの「ベクトル」は「数を$n$個並べたもの」であって、その足し算も定義がすでに行われていた。ここで考えているのは逆に、具体的な内容(数が$n$個で表されているとか)を考えずに「こんな演算ができる空間があったとしたら」という仮定を出発点に置く。
FAQ:交換則や結合則が成り立たない加法ってあるんですか?
ここで書いている「加法」は「いわゆる普通の足し算」とは限らない。「いわゆる普通の足し算」ではない演算を持ってきて、それがベクトル空間になるかどうかを判断する。たとえば「この空間における加法とは二つの実数の平均を取る操作である」という定義を取ることができるが、その定義では結合法則が成り立たず、ベクトル空間ではない。数学では、なるべく一般的に物を考えようとするので、「当たり前」と思うところも前提として(ということはつまり、当たり前じゃないものも存在していると考えて)「そういう前提があれば何が言えるか」を考えていくのである。
我々はこの後しばらく「この公理が満たされるならどんな結果が導けるか」を考えていく。そうしておくことで後である空間がベクトル空間であると判明したならば、「○○の定理が使える」と即座に判断できるわけである。
これらはいずれも「何を当たり前のことを」と言いたくなるほどに「当たり前」の条件である。それは我々が普段使っている量がすでに「ベクトル空間」に属する量だからである。
○○と○○の線形結合は○○
の○○の全てが、考えているベクトル空間の中に存在していなくてはいけない、ということである。
いくつかの実例をみておこう。
もっともつまらないベクトル空間は$\avec{0}$だけを含む集合である。加法は「$\avec{0}+\avec{0}=\avec{0}$」で定義し、スカラー倍を「$\avec{0}$に何を掛けても$\avec{0}$」で定義すれば、ベクトル空間の公理をすべて満たす(とはいえ、つまらない)。
実数は通常の加法の定義においてベクトル空間をなす。単位元と逆元があることは自明として、実数と実数の線形結合は実数だからである。
「ベクトルとは矢印で表せるもの」とか「ベクトルは向きと大きさがあるもの」と習った人には、単なる実数が「ベクトル」と呼ばれることには違和感があると思うが、ここでの「ベクトル」はそういう定義なのだ。
ただし、条件の中の「スカラー」が複素数だと線形結合を取ると複素数になってしまうから、スカラーが実数でないとベクトル空間にならない。
同様に、複素数と複素数の線形結合は複素数なので、複素数もベクトル空間である(こちらはスカラーは実数でも複素数でもよいが、複素数にするのが普通である)。
もちろん、数ベクトル$\vec A$(3次元の場合に成分で表現すれば、$(A_x~A_y~A_z)$となる)は上の全ての条件を満たす。
普通に思いつく「ベクトル」よりも「大きな」ものも「ベクトル」の範疇に入る。たとえばある共通の定義域($a\lt \xcol{x}\lt b$}など)で定義された関数$f\kakko{\xcol{x}}$は立派なベクトルである。
「当たり前」とは言ったが、なかには上の条件を満たさないようなものもある。たとえば「自然数」の集合を考えると、交換則と結合則は満たすが、単位元($\avec{0}$はこの場合、数の0である)は「自然数」には含まれないし、$a$の逆元となる$-a$は負の数であるから「自然数」に含まれない。
ベクトル空間の公理を満たすならば、その空間では
単位元の唯一性
ベクトル空間には単位元は一つしかない。
逆元の唯一性
ベクトル空間の一つの元$\avec{a}$に対して逆元$-\avec{a}$は一つしかない。
のような定理が満たされる。
簡単なので問題としてやっておこう。
上の二つの結果を証明せよ。答えがわかってから開くこと。
単位元について。$\avec{0_2}$は単位元であるから、任意の$\avec{a}$に対して$\avec{a}+\avec{0_2}=\avec{a}$を満たす。よって、$\avec{0_1}+\avec{0_2}=\avec{0_1}$である。交換則を使うと、$\avec{0_1}+\avec{0_2}=\avec{0_2}+\avec{0_1}$であり、$\avec{0_1}$もまた単位元であるなら、$\avec{0_2}+\avec{0_1}=\avec{0_2}$となる。よって$\avec{0_2}=\avec{0_1}$である。すなわち単位元は一つしかない。
逆元について。$\avec{a}$の逆元が$\avec{b},\avec{c}$のように二つあったと仮定する。$\avec{b}+\avec{a}+\avec{c}$に結合法則を使うと
\begin{align}
\avec{b}+\goverbrace{\avec{a}+\avec{c}}^{先に計算}
=& \goverbrace{\avec{b}+\avec{a}}^{先に計算}+\avec{c}\nonumber\\
\avec{b}=&\avec{c}
\end{align}
となる。よって逆元は一つ。
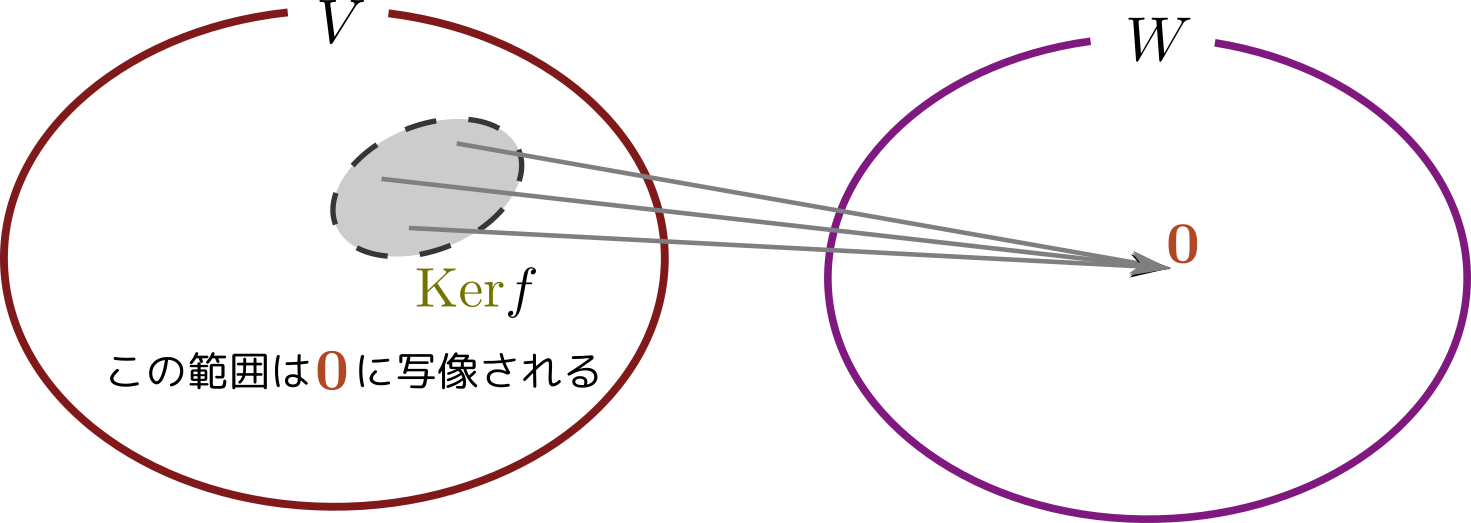
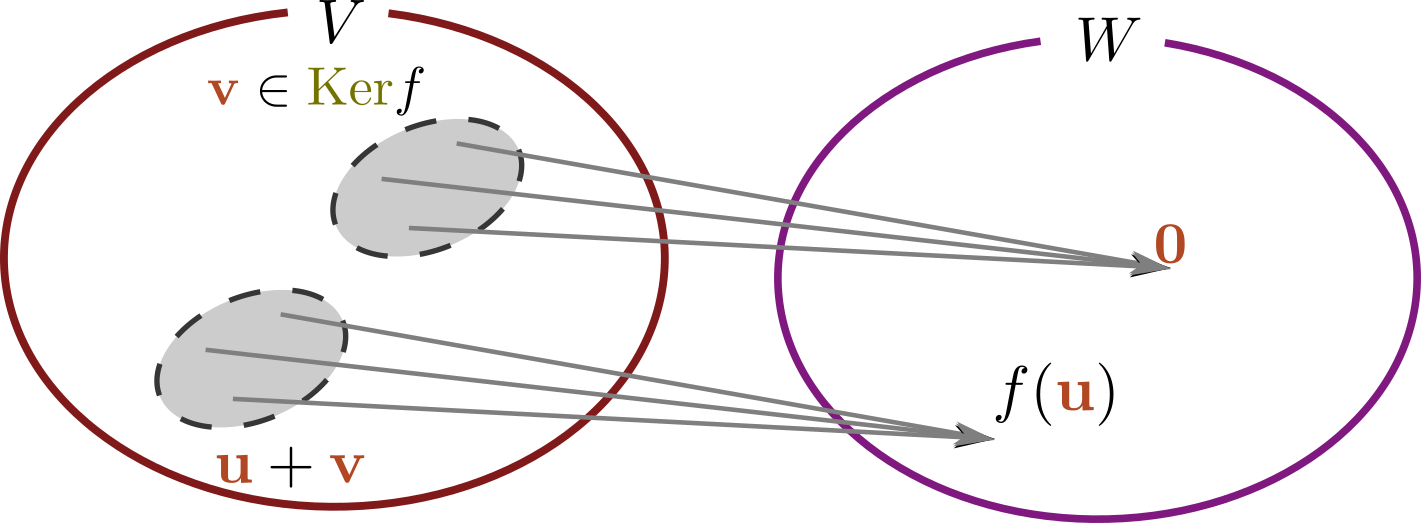
 のように変形できることをのあたりで示したが、この$\mt{0}$になっている列がかかる相手が$\Ker\mt{M}$である。この行列を掛けると、
のように変形できることをのあたりで示したが、この$\mt{0}$になっている列がかかる相手が$\Ker\mt{M}$である。この行列を掛けると、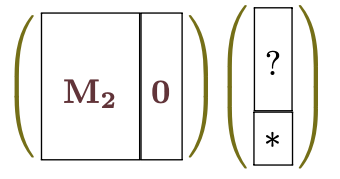
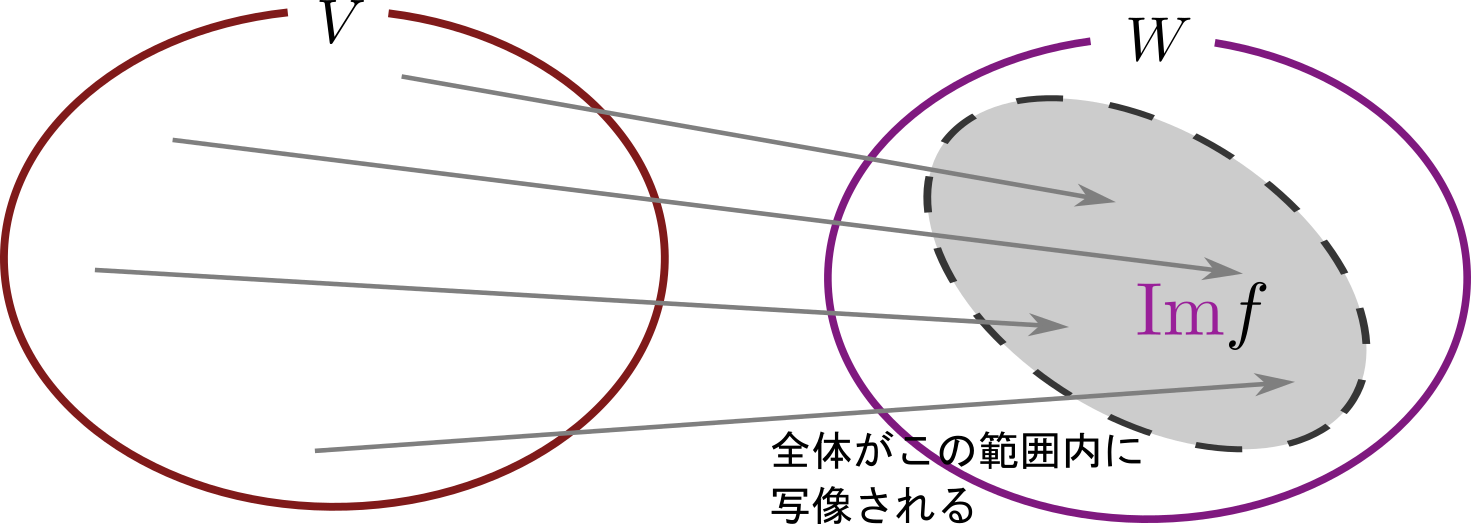
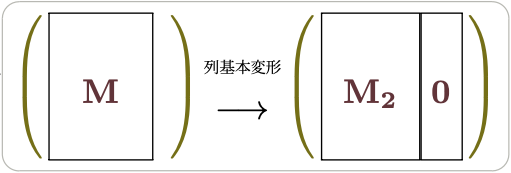
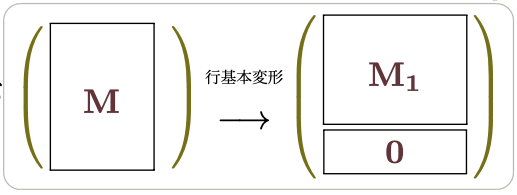 のように変形できることを示したが、この$\mt{0}$になっている行以外の部分が$\Img\mt{M}$である。
のように変形できることを示したが、この$\mt{0}$になっている行以外の部分が$\Img\mt{M}$である。