「物理数学Ⅰ」2021年度講義録第12回

前回の感想・コメントシートから

　前回の授業の「感想・コメント」の欄に書かれたことと、それに対する返答は、

にありますので見ておいてください。

固有ベクトル

　行列で表現できる線形変換では、ベクトルが別のベクトルへと「変換」される。以下では、変換前のベクトルのいる空間と変換後のベクトルのいる空間が同じ$V$である場合を考えよう。つまり、今から考える写像（変換）は同じベクトル空間の間の演算（$V\to V$）だ（行列で表現すれば正方行列だ）とする。よってこの章で登場する行列はすべて正方行列である。

　固有ベクトルを理解するためのアプリは、前にも使った↓です。

　アプリの固有ベクトルに関する話の説明ビデオは↓

　正方行列による変換の様子を見ていると、多くの線形変換に対して「大きさは変わるが向きが変わらないベクトル」があることに気づく。

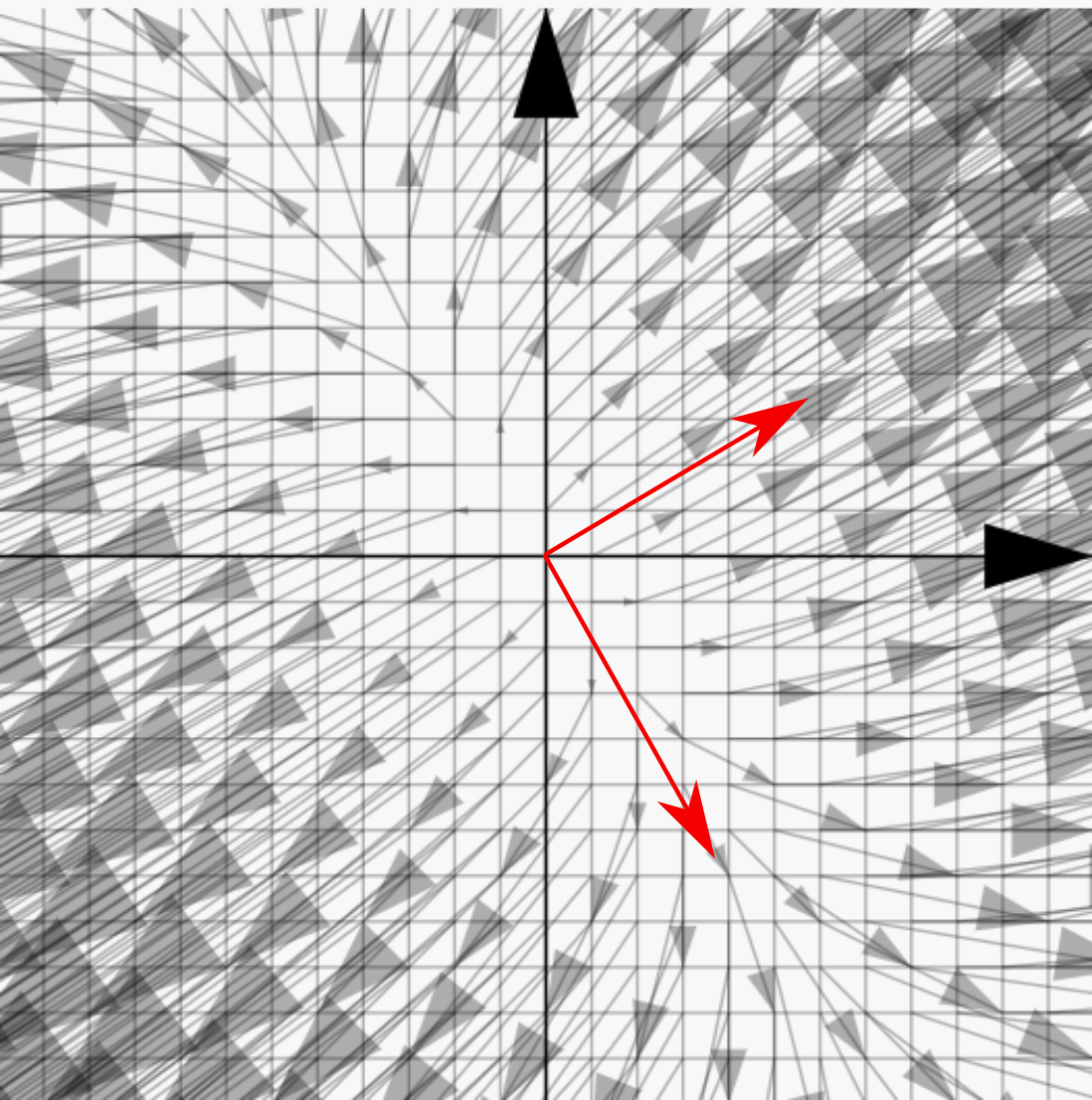
　↑の図は、行列$\mtx{3&1\\1&2}$による写像による点の移動を矢印で表現したものだが、これを見ていると赤矢印で示した二つの方向については変換による点の移動が「原点にから離れる向き」になっている（つまり、ベクトルの向きが変わらない）ことがわかる。

　↑このあたりはアプリをじっくりといじくってみること。絵で感覚をつかむのは大事である。

固有ベクトルの定義

固有ベクトルの定義と例についてのビデオ↓

以下は文章による説明。

　一般に、ある演算子$\ope{\cal O}$（行列で表現されていてもいいし、微分演算子などでもよい）を$\avec{0}$ではない、あるベクトル$\avec{v}$に掛けたときに元のベクトルのスカラー倍になるのは特別なベクトルの場合に限る。この特別なベクトルに名前をつけよう。つまり

固有ベクトル

線形演算子$\ope{\cal O}$と零ベクトルではないベクトル$\avec{v_\lambda}$とスカラー量$\lambda$の間に \begin{equation} \ope{\cal O}\avec{v_\lambda}=\lambda\avec{v_\lambda}\label{defofeigenvector} \end{equation} なる関係が成り立つとき、$\avec{v_\lambda}$を「$\ope{\cal O}$の固有ベクトル(eigenvector)」と呼び、スカラー$\lambda$のことを「固有値(eigenvalue)」と呼ぶ。

eigenはドイツ語の「固有」。歴史的な理由でドイツ語が使われる。eigen vectorと分けて表記する場合もある。$\ope{\cal O}$が微分演算子である場合は「固有関数(eigenfunction)」と呼ぶことが多い。

　「$\lambda$は$\ope{\cal O}$の（$\avec{v_\lambda}$に対する）固有値である」とか、「$\avec{v_\lambda}$は固有値$\lambda$の$\ope{\cal O}$の固有ベクトルである」のように表現する。このことは、

固有ベクトル$\avec{v_\lambda}$の前にある線形演算子$\ope{\cal O}$は、スカラー$\lambda$に置き換えてよい。

ことを意味する。演算子がスカラーに「化ける」のだから、計算をかなり簡単にしてくれる。

　シンプルな例をいくつか示しておこう。行列$\mtx{a&0\\0&b}$のような簡単な行列なら、固有ベクトルは$\mtx[c]{1\\0}$と$\mtx[c]{0\\1}$であり、固有値はそれぞれ$a$と$b$である。

　行列$\mtx{0&1\\ 1&0}$は「上下成分を入れ替える$\mtx[c]{x_1\\ x_2}\to \mtx[c]{x_2\\ x_1}$行列」だから、固有ベクトルは$\mtx[c]{1\\1}$（入れ替えても同じ）と$\mtx[c]{1\\-1}$（入れ替えると逆符号）である。固有値はそれぞれ1と$-1$となる。

　行列でない演算子に対しても固有値・固有ベクトルは定義できる。もっとも簡単な例は微分演算子$\opcol{\diff \over \kidx}$に対する固有ベクトルである指数関数$\E^{K\xcol{x}}$である（固有値は$K$）。$\opcol{\diff \over \kidx}\E^{K\xcol{x}}=K\E^{K\xcol{x}}$という式を見るとわかる。

　なお、固有値が0の固有ベクトル（$\ope{\cal O}\avec{v_0}=0$を満たすベクトル）が存在することは$\Ker{\ope{\cal O}}$が$\{\avec{0}\}$ではないことを意味する。

　以下では$\avec{v_\lambda}$が複素数$N$成分のベクトル（${\mathbb C}^N$）であり、$\ope{\cal O}$が$N\times N$行列$\mt{M}$である場合を考えよう。なお、行列を掛けるときは、

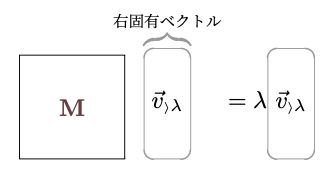
のように行列を左から、右にある列ベクトルに掛ける場合と

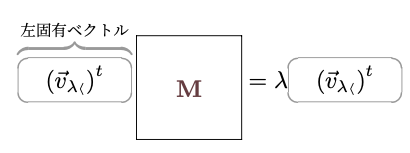
のように左にある行ベクトルに行列を右から掛ける場合が考えられるので、この二つの固有ベクトルを「右固有ベクトル」と「左固有ベクトル」と呼んで区別する（$\lambda$の横につけた$\langle$または$\rangle$は「開いている方の方向から行列を掛けてね」という向きを表す）。後で示すが、これらの固有値の組は同じになるが、右固有ベクトルと左固有ベクトルは一般には一致しない。

左固有ベクトルと右固有ベクトルが同じになる例を扱うことが多いので、このことを失念しやすい。

　行列が対称行列ならばスカラー倍をのぞいて一致し、$\vec v_{\lambda{\scriptscriptstyle \langle}}=\alpha_{\lambda}\vec v_{{\scriptscriptstyle \rangle}\lambda}$（$\alpha_\lambda$は任意のスカラー）となる。また、行列がエルミート行列なら、$(\vec v_{\lambda\fromR})^*=\alpha_\lambda\vec v_{\fromL\lambda}$となる（$*$が必要、ただしここで固有値には$*$は不要である。後で説明する）。

固有ベクトルの相互関係

　以下の話の説明ビデオは↓

固有値のそれぞれ違う固有ベクトルの組は線形独立である

　固有値のそれぞれ異なる固有ベクトルの組は線形独立である。

　ゆえに、$n$次元ベクトル空間の固有ベクトルは最大でも$n$本である。

ということが証明できる。以下の練習問題をやってみよう。

上の前半、すなわち、固有値がそれぞれ$\lambda_i$である固有ベクトルの組$\avec{v_i}(i=1,2,\cdots,K)$（$\allc{\lambda_*}$は互いに異なる値を持つ）は、いかなる係数$\alpha_i$を使っても（全てが0である場合を除き） \begin{align} \sum_{\dum[ycolor]i=1}^K\alpha_{\dum[ycolor]{i}} \avec{v_{\dum[ycolor]i}}=0\label{ldeigen} \end{align} が成り立つことはないことを示せ。

　このことから、$n\times n$行列に対する固有値は最大でも$n$個しかないことがわかる（$n$次元空間では線形独立なベクトルは最大でも$n$本である）。ただし、固有値の数が$n$より少ないことは有り得る（後でどのような場合にそうなるかを考えよう）。

　固有値と内積に関しては以下の定理が知られている。

固有値の違う左固有ベクトルと右固有ベクトルは直交する

$\lambda_1\neq\lambda_2$のとき、$\vec v_{{\lambda_1}{\scriptscriptstyle \langle}}\cdot {\vec v_{{\fromL}{\lambda_2}}}=0$である。

　これを証明するには、左固有ベクトルと右固有ベクトルの間に行列$\mt{M}$を挟んだ式（下の二つの式の左辺）を、以下のように2種類の方法で計算する。 \begin{align} \gunderbrace{\yokovec{\vec v_{{\lambda_1}{\scriptscriptstyle \langle}}} \,\mt{M}}_{こっちを\atop 先に計算}\tatevec{\vec v_{{\lambda_2}{\fromL}}}=&\yokovec{\lambda_1\vec v_{{\lambda_1}{\scriptscriptstyle \langle}}} \tatevec{\vec v_{{\fromL}{\lambda_2}}}=\lambda_1\vec v_{{{\lambda_1}\scriptscriptstyle \langle}}\cdot {\vec v_{{\lambda_2}{\fromL}}} \\ \yokovec{\vec v_{{\lambda_1}{\scriptscriptstyle \langle}}}\,\gunderbrace{\mt{M}\tatevec{\vec v_{{\fromL}{\lambda_2}}}}_{こっちを\atop 先に計算}=&\yokovec{\vec v_{{\lambda_1}{\scriptscriptstyle \langle}}} \tatevec{\lambda_2\vec v_{{\fromL}{\lambda_2}}}=\lambda_2\vec v_{{\lambda_1}{\scriptscriptstyle \langle}}\cdot {\vec v_{{\fromL}{\lambda_2}}} \end{align} 上の二つの式を辺々引くことにより、 \begin{align} 0= (\lambda_1-\lambda_2){\vec v_{{\lambda_1}{\scriptscriptstyle \langle}}}\cdot{\vec v_{{\fromL}{\lambda_2}}} \end{align} を得るが、 $\lambda_1\neq\lambda_2$なので${\vec v_{{\lambda_1}{\scriptscriptstyle \langle}}}\cdot{\vec v_{{\fromL}{\lambda_2}}}=0$とわかる。

この定理の応用として、 \begin{align} m,nが整数で、m\neq nならば \int_0^\pi \sin m \thetacol{\theta}\sin n\thetacol{\theta}=0 \end{align} を、$\int_0^\pi \sin m \thetacol{\theta}\left({\diff \over \diff \theta}\right)^2\sin n\thetacol{\theta}$を2通りの計算で計算することから示すことができる。やってみよ。

前回の感想・コメントシートから対称行列とエルミート行列の固有値

対称行列とエルミート行列の固有値

　以下の話の説明ビデオは↓

対称行列の場合

　行列が対称行列$\mt{M}=\mt{M^t}$なら、左固有ベクトルと右固有ベクトルには違いがない。転置することによって \begin{align} \mt{M}\vec v_{{\fromL\lambda}}=\lambda\vec v_{\fromL\lambda}~~~\overset{転置}{\longrightarrow}~~~~ \left(\vec v_{{\fromL\lambda}}\right)^t \mt{M^t}=\lambda \left(\vec v_{{\fromL\lambda}}\right)^t \end{align} が示せるからである。

エルミート行列の場合

　なお、「転置してさらに複素共役を取る」という操作を「エルミート共役」、「エルミート共役を取っても変わらない行列」を「エルミート行列」と呼ぶが、行列がエルミート行列の場合は、 \begin{align} \mt{M}\vec v_{{\fromL\lambda}}=\lambda\vec v_{\fromL\lambda}~~~\overset{エルミート共役}{\longrightarrow}~~~~ \left(\vec v_{{\fromL\lambda}}\right)^\dagger \mt{M^\dagger}=\lambda^* \left(\vec v_{{\fromL\lambda}}\right)^\dagger \end{align} が言える。つまり左固有ベクトルは右固有ベクトルの$\dagger$である。

　実はエルミート行列の場合、$\left(\vec v_{{\fromL\lambda}}\right)^\dagger\mt{M}\vec v_{\fromL\lambda}$を \begin{align} \gunderbrace{\left(\vec v_{{\fromL\lambda}}\right)^\dagger\mt{M}}_{\lambda^*\left(\vec v_{{\fromL\lambda}}\right)^\dagger}\vec v_{\fromL\lambda}=& \left(\vec v_{{\fromL\lambda}}\right)^\dagger\gunderbrace{\mt{M}\vec v_{\fromL\lambda}}_{\lambda\vec v_{\fromL\lambda}}\nonumber\\ \lambda^* \left(\vec v_{{\fromL\lambda}}\right)^\dagger\vec v_{\fromL\lambda} =&\lambda \left(\vec v_{{\fromL\lambda}}\right)^\dagger\vec v_{\fromL\lambda} \end{align} のように二通りの計算方法で計算することで、$\lambda=\lambda^*$が言える。つまりエルミート行列の固有値は実数である。

固有ベクトルの相互関係特性方程式

特性方程式

以下の内容の説明ビデオが↓

特性方程式と特性多項式

　固有値の定義式$\ope{\cal{O}}\avec{v}=\lambda\avec{v}$は、 \begin{align} \left(\ope{\cal O}-\lambda\right)\avec{v}=0 \end{align} と変形できる。これから、演算子$\left(\ope{\cal O}-\lambda\right)$には逆があってはいけない（あったら、$\avec{v}=0$になってしまう）。

　このことは、演算子$\ope{\cal O}$が$N\times N$行列$\mt{M}$で表現される場合、

特性方程式

\begin{align} \det\kakko{\mt{M}-\lambda\mt{I_\sN}}=0\label{tokusei} \end{align}

が満たされなくてはいけないことを意味する。この式を「特性方程式」または「固有方程式」と呼び、左辺に現れる

特性多項式

\begin{align} \phi_{\mt{M}}\kakko{\xcol{x}}=\det\kakko{\mt{M}-\xcol{x}\mt{I_\sN}}\label{tokuseiP} \end{align}

を「特性多項式」と呼ぶ。特性多項式は \begin{align} \det\mtx[cccc]{M_{11}-\xcol{x}&M_{12}&\cdots&M_{1\sN}\\M_{21}&M_{22}-\xcol{x}&\cdots&M_{2\sN}\\ \vdots&\vdots&\ddots&\vdots\\ M_{\sN1}&M_{\sN2}&\cdots&M_{\sN\sN}-\xcol{x}} \end{align} と書くことができ、対角成分の積$(M_{11}-\xcol{x})(M_{22}-\xcol{x})\cdots(M_{\sN\sN}-\xcol{x})$を含み、これから出てくる項$(-1)^\sN\xcol{x}^N$以外に$\xcol{x}$の$N$次の項は出てこないから、$\xcol{x}$に関して$N$次の多項式$\alpha_0+\alpha_1\xcol{x}+\alpha_2\xcol{x}^2+\cdots+(-1)^N\xcol{x}^N$である（$\allc{\alpha_*}$は$\ope{\cal O}$を決めれば決まる定数）。この式を$(-1)^N$で割ってから因数分解して$=0$と置くと \begin{align} (\xcol{x}-\lambda_1) (\xcol{x}-\lambda_2) \cdots (\xcol{x}-\lambda_\sN)=0\label{eigeneq} \end{align} となり、この式の$N$個の解が固有値$\lambda_1,\lambda_2,\cdots,\lambda_\sN$である。

ここまで「左固有ベクトル」と「右固有ベクトル」を区別しつつ「左固有値」と「右固有値」を区別しなかった。もし左固有値と右固有値が違う数列であったとすると、特性多項式が「左固有値を使った因数分解」と「右固有値を使った因数分解」の二つを持つことになってしまう。しかし多項式の因数分解は一意的である。よって左固有値の数列と右固有値の数列は等しい。

　ここまでの話を聞くと「固有値は$N$個ある」と思ってしまいがちだが、二つの理由で$N$個ない場合がある。

重解を持つ場合上の多項式の一部が$(\lambda-\lambda_i)^k(kは整数で、k>1)$となっている場合である。この場合、$k-1$個だけ固有値の数が減る。
実ベクトルを考えていて、複素数解の場合 実ベクトル空間を考えている場合、$\lambda_i$が複素数だと$\lambda_i\avec{v}$が考えているベクトル空間の外に出てしまうから、たとえ$\ope{\cal O}\avec{v}=\lambda_i\avec{v}$が満たされていても、これは固有ベクトルとは言えない。

対称行列とエルミート行列の固有値 $2\times2$行列の実例

$2\times2$行列の実例

　$2\times2$行列の場合で例を示す。まず重解でない場合を考える。 \begin{equation} \mtx{2&-1\\3&6}\rv{x\\y}=\lambda\rv{x\\y} \end{equation} となるようなベクトル$\rv{x\\y}$を求めよう。上の式を \begin{equation} \mtx{2-\lambda&-1\\3&6-\lambda}\rv{x\\y}=\rv{0\\0}\label{lambdaxx} \end{equation} と変形する。この行列$\mtx{2-\lambda&-1\\3&6-\lambda}$に逆行列があってはならないから \begin{equation} \det\mtx{2-\lambda&-1\\3&6-\lambda}=0 \end{equation} が成り立たねばならない。これから \begin{equation} \begin{array}{rl} (2-\lambda)(6-\lambda)-(-1)\times 3&=0\\ 15-8\lambda+\lambda^2&=0\\ (\lambda-3) (\lambda-5) &=0 \end{array} \end{equation} という特性方程式が出てくる。ゆえに、$\lambda$は3か5でなくてはいけない。

　$\lambda=3$}である場合は \begin{equation} \mtx{-1&-1\\3&3}\rv{x\\y}=\rv{0\\0} \end{equation} となる。これはあきらかに、$y=-x$であることを示している。一方$\lambda=5$である場合は、 \begin{equation} \mtx{-3&-1\\3&1}\rv{x\\y}=\rv{0\\0} \end{equation} であるから、$y=-3x$であるということになる。こうして、固有値$3$を持つ固有ベクトル$\mtx[c]{1\\-1}$と、固有値5を持つ固有ベクトル$\mtx[c]{1\\-3}$が見つかった。

　$2\times2$行列で特性方程式が重解になる例をやっておくと、一つは単位行列に比例する行列$\mtx{a&0\\0&a}$で、これの特性方程式は$(\lambda-a)^2=0$になり、固有値は2のみである。ただし、この場合任意のベクトルは固有ベクトルである（つまり、独立な固有ベクトルの本数は2）。もう少し複雑な重解になる例を挙げると行列$\mtx{1&-1\\1&3}$で、固有値方程式は \begin{align} \det\mtx{1-\lambda&-1\\1&3-\lambda}=& (1-\lambda)(3-\lambda)-(-1)\times 1 \nonumber\\ =& \lambda^2 -4\lambda+4=(\lambda-2)^2 \end{align} で、固有値は2しかない。この場合の固有ベクトルは \begin{align} \mtx{-1&-1\\1&1}\vec v_{\fromL 2}=0 \end{align} を満たすベクトルなので、独立なものは$\mtx[c]{1\\-1}$の1本しかない。左固有ベクトルは$\vec v_{2\fromR}=\mtx{1\\1}$、つまり、$(\vec v_{2\fromR})^t=\mtx{1&1}$である。

　二次方程式を解くとき「重解は珍しい」という経験をしているんだろう。同様に特性方程式が重解になる行列はある意味「珍しい」行列である。行列のパラメータを変えていくと、パラメータ空間内の孤立した点として「固有方程式が重解になる行列」が出現する。

　固有値の数が減る場合でも、固有ベクトルの数も減る場合とそうならない場合があることに注意（後で一般論を考える）。

　複素数解となるシンプルな例を一つやっておこう。行列$\mtx{0&-1\\1&0}$を考えると、特性方程式は \begin{align} \det\mtx{-\lambda &-1\\ 1&-\lambda}=&0\nonumber\\ -\lambda^2 -1 =&0 \end{align} となり、この方程式の解は$\lambda=\pm\I$であって実数解がない。この行列は「${\pi\over 2}$回転」の行列なので「回転しても元と同じ方向を向いているベクトル」がないのは当然といえば当然である。

　なお、複素ベクトル空間だと、 \begin{align} \mtx{\mp\I &-1\\ 1&\mp\I}\vec v_{\fromL\pm\I}=0 \end{align} より、$\vec v_{\fromL\pm\I}=\mtx[c]{1\\ \mp\I}$という固有ベクトルが存在する。掛け算してみると \begin{align} \mtx{0&-1\\1&0}\mtx[c]{1\\ \mp\I}=\mtx[c]{\pm\I\\ 1}=\pm\I\mtx[c]{1\\ \mp\I} \end{align} となってこれは確かに固有ベクトルになっている。

特性方程式 $2\times2$行列の一般論

$2\times2$行列の一般論

　以下の話の説明ビデオは↓

　例で感じをつかんだところで、一般的に考えていこう（ここではベクトル空間は${\mathbb C}^2$とする）。一般の$2\times2$行列を$\mt{M}=\mtx{a&b\\c&d}$と書くと、$\mt{M}-\lambda\mt{I_2}$が逆行列を持ってはいけないので、 \begin{align} \det\mtx{a-\lambda&b\\ c&d-\lambda}=&0\nonumber\\ (a-\lambda)(d-\lambda)-bc =&0\nonumber\\ \lambda^2-(a+d)\lambda +ad-bc=&0\label{tokutwo} \end{align} という式が出る。これから固有値が \begin{align} \lambda_\pm ={a+d\pm\sqrt{(a+d)^2-4(ad-bc)}\over 2} ={a+d\pm\sqrt{(a-d)^2+4bc}\over 2} \end{align} であることがわかる。重解でない場合（$(a-d)^2+4bc\neq0$の場合）、固有ベクトルは固有値二つに対応して2本あるので、 \begin{align} \mtx{a-\lambda_\pm&b\\c&d-\lambda_\pm}\vec v_{\fromL\lambda_\pm}=&\vec 0\\ \end{align} を解こう（以下しばらくは重解でない場合のみを考える）。

　解は \begin{align} \vec v_{\fromL\lambda_\pm}=\mtx[c]{b\\ \lambda_\pm -a}または\mtx[c]{\lambda_\pm-d \\ c}\label{eigeneqtwo} \end{align} ある。複号がある式が二つなので、一見四つの解があるように見えるが、もちろん独立なベクトルは2本しかない。

　以下の式は簡単にしめすことができる。

$(\lambda_\pm-d)\mtx[c]{b\\\lambda_\pm-a}=b\mtx[c]{\lambda_\pm-d\\c}$
$(\lambda_\pm-a)\mtx[c]{\lambda_\pm-d\\ c}=c\mtx[c]{b\\\lambda_\pm-a}$

　以上より、$b$が0でない場合は$\mtx[c]{b\\ \lambda_+ -a}$と$\mtx[c]{b\\ \lambda_- -a}$という独立な固有ベクトル2本を得る。$c$が0でないなら$\mtx[c]{\lambda_+-d\\ c}$と$\mtx[c]{\lambda_- -d\\ c}$でもよい。

　上の1.の式は$b=0$のときは$0=0$という意味のない式になる。同様に2.の式は$c=0$のとき意味のない式となる。

　$b$または$c$が0のとき、すなわち$bc=0$の場合が心配になるが、そのときは$(\lambda_\pm-a)(\lambda_\pm -d)=0$が成り立つので$\lambda_\pm$の片方は$a$、もう片方が$d$になり、「四つの解」は \begin{align} \mtx[c]{b\\0},\mtx[c]{b\\ d-a},\mtx[c]{a-d\\c},\mtx[c]{0\\c} \end{align} となるので$\mtx[c]{b\\d-a}$と$\mtx[c]{a-d\\c}$の2本を独立な固有ベクトルと選んでおけばよい。$b$も$c$も0のときは、もっと簡単に$\mtx[c]{1\\0}$と$\mtx[c]{0\\1}$としても同じことである。「$a=d$だと困る」と思うかもしれないが、それは重解のケースに対応するので、以下で別に考える。

$2\times2$行列の実例重解の場合

重解の場合

　重解である場合は、$\lambda$が一つの解$\lambda_1={a+d\over 2}$しかない。まず$b=0$または$c=0$の場合を考えよう。重解のときは$(a-d)^2+4bc=0$が成り立つので、$b,c$が0になると$a=d$になる。$b$も$c$も0である場合は、元々の行列が単位行列に比例する（$a\mt{I}$または$d\mt{I}$）。この場合は固有ベクトルは$\mtx[c]{1\\0}$と$\mtx[c]{0\\1}$の2本となる。このように、2本以上の互いに独立な固有ベクトルが同じ固有値を持つとき、「固有値が縮退(degenerate)する」と表現する（量子力学でよく使う表現である）。

$b=0$で$c\neq0$の場合は行列が$\mtx{a&0\\c&a}$の形になるので、固有ベクトルは$\mtx[c]{0\\1}$しかない。$c=0$で$b\neq0$の場合は行列は逆で、固有ベクトルは$\mtx[c]{1\\0}$の1本になる。

　次に$bc\neq0$の場合を考える。この場合固有ベクトルが満たすべき式は \begin{align} \mtx{a-\lambda_1& b\\ c&d-\lambda_1}\mtx[c]{v_{x}\\ v_{y}}=&0\nonumber\\ \mtx{{a-d\over 2}& b\\ c&{d-a\over 2}}\mtx[c]{v_{x}\\ v_{y}}=&0 \end{align} であり、固有ベクトルは$\mtx[c]{-b\\ {a-d\over 2}}$か$\mtx[c]{{d-a\over 2}\\ -c}$である（これら二つは比例するので、どっちでも同じ）。

　$2\times2$行列の場合、以下のことが言える。固有値が2個（すなわちベクトル空間の次元と同じ数）あるときは常に固有ベクトルが2本見つかる。固有値が1個しかないときは、固有ベクトルが2本ある場合と、1本しかない場合がある。固有値が一つもないということはありえない。

　ただし、以上は${\mathbb C}^2$で考えた結果である。もしベクトル空間が${\mathbb R}^2$なら、固有値が複素数になることは許されない（固有ベクトルも複素数の成分を持てない）。その場合は固有値や固有ベクトルが一つもない、という状況が有り得る。

　以上で第11回の授業は終わりです。webClassに行って、アンケートに答えてください。

物理数学I webclass

この感想・コメントシートに書かれたことについては、代表的なものに対しては次のページで返答します。

　なお、webClassに情報を載せていますが、木と金の11:50〜12:50の間、オンラインオフィスアワーとしてzoomを開いてます。質問や相談などがある人は来て話してください。参加者が少ないので、物理系１年生向けのオフィスアワーと合同になってます。

テキストのPDF版はこちらです。

$2\times2$行列の一般論受講者の感想・コメント

受講者の感想・コメント

「固有値の違う右固有ベクトルと左固有ベクトルは直行する」という説明のところで、v〉λ２とvλ２〉の２種類の表記があったのですが、この表記の分け方って何か意味があるのでしょうか？

あ、すいません、特に意味はないです。どっちでも同じ（統一しておくべきでした）。

固有値と固有ベクトルについて考えるときに、固有値は同じなのに左右でベクトルが違う例などは面白いと思ったが、重解や複素数解になるときを考えたり、重解の中でも固有値一つに対してベクトルが一つなのか二つなのか考えなければならないのはこれらのパターンをそれぞれ理解しておかなければならないのが大変だなと感じた。

複素数解は別にやることは増えないです。重解はたしかにめんどくさい。その変わり、あまりでてこない。

固有ベクトルに右左があるのは初めて知った。固有値とそれに対応する固有ベクトルを求める作業は少し面倒に感じたが計算は楽しいと思えた。

対称行列やエルミート行列のときは左右を区別しなくていいので、そっちばっかりやっていると左右があることを忘れる傾向があります。そうじゃないこともあることには注意。

今回の授業では自分は固有ベクトルについてあまりわかっていなかったのですが固有ベクトルとその性質を理解することができ、また、固有ベクトルを考える意味が分かりました。他にも特性方程式がどのようなものかを理解することができたので、しっかり復習してこれらを使える（計算できる）ようにしていきたいと思いました。

計算練習してみてください。

慣れてくるとそう大変でもないので、練習してみてください。

重解の場合