特性方程式が重解を持つ場合の三角行列化
特性多項式が以下のように因数分解されたとしよう。 \begin{align} \phi_{\mt{M}}\kakko{\xcol{x}}= (\xcol{x}-\lambda_1)^{m_1} (\xcol{x}-\lambda_2)^{m_2}\cdots (\xcol{x}-\lambda_k)^{m_k}\label{mklambda} \end{align} $k$は固有値の数で、$N$より小さい整数である。
ここで$\allc{m_*}$は$\sum_{\dum{j}=1}^k m_{\dum{j}}=N$を満たす1以上の整数（$k$は1以上$N$以下の整数となる）で、$m_i$を固有値$\lambda_i$の「重複度」と呼ぶ。すべての重複度$\allc{m_*}$が1ならば前節で考えた場合になる。
特性方程式が重解を持つときでもCayley-Hamilton定理は成り立ち、 \begin{align} (\mt{M}-\lambda_1)^{m_1} (\mt{M}-\lambda_2)^{m_2}\cdots (\mt{M}-\lambda_k)^{m_k}=\mt{0}\label{mklambdaM} \end{align} である。
前に述べたように「重解」になるのはたくさんの行列のうちの孤立した「珍しいもの」だけだである。
たとえば$\mtx{1&1\\-1&3}$は特性方程式が$\lambda^2-4\lambda+4=0$になって重解を持つのだが、これをちょっとだけ変えた行列$\mtx{1&1+\epsilon\\-1&3}$の特性方程式は$\lambda^2-4\lambda+4+\epsilon=0$になって、たとえ$\epsilon$が小さくとも重解ではない。
「重解」の場合の周囲に存在する「重解にならない行列」からの連続的極限の先に「重解になる行列」があると考えれば「重解でない場合に成り立つ式は重解の場合でも成り立ちそうだな」と予想される（その方向で証明する方法もある）。
ここでは三角行列化を使った証明を行う。特性方程式に重解があったとしても、固有ベクトルが$N$本見つかったなら前項の証明はそのまま繰り返すことができる。ここでは固有ベクトルが$k$本$(k\lt N)$しか見つからなかった場合を考えよう。そのとき、固有ベクトル以外に「固有ベクトルとは独立なベクトル」が$N-k$本見つかる。これらのベクトルは後で説明する「一般化固有ベクトル(generalized eigenvector)」になっている。
それらを$\allc{\vec V_*}$として \begin{align} \mt{P_1}=\mtx[c@{}c@{}cc@{}c@{}c]{ \nagatatevec{\vec v_{\fromL\lambda_1}}&\cdots&\nagatatevec{\vec v_{\fromL\lambda_k}} &\nagatatevec{\vec V_{1}}&\cdots&\nagatatevec{\vec V_{N-k}}} \end{align} のような行列を作る。ここで使った列ベクトルは全て独立だから、逆行列を \begin{align} \mt{(P_1)^{-1}}=\mtx[c]{\nagayokovec{~~\vec v^{\lambda_1\fromR}~~}\\[-1mm]\vdots\\\nagayokovec{\vec v^{\lambda_k\fromR}}\\\nagayokovec{\vec V^{1}}\\ \vdots\\\nagayokovec{\vec V^{N-k}}} \end{align} のように作ることができる。これらを使って、 \begin{align} \mt{(P_1)^{-1}MP_1}=&\mtx[ccc@{}c@{}|c]{ \lambda_1&\cdots&0&&\\ \vdots&\ddots&\vdots&&*\\ 0&\cdots&\lambda_k&&\\\hline &\mt{0}&&&\mt{M_1} } \end{align} のように「一部対角化」できる。
ここで対角化できた部分を$\mt{D_1}$、$*$の部分を$\mt{X_1}$と書いて、$ \mt{(P_1)^{-1}MP_1}=\mtx{\mt{D_1}&\mt{X_1}\\\mt{0}&\mt{M_1}}$としておこう。
この結果はまだ対角行列でも上三角行列でもないが、ここでさらに \begin{align} \mt{P_2}=\mtx[cc]{\mt{I}&\mt{0}\\\mt{0}&\mt{p_2}} \end{align} を使って、すでに対角化された$\mt{D_1}$の部分を壊さないようにしつつ、 \begin{align} \goverbrace{\mtx{\mt{I}&\mt{0}\\ \mt{0}&\mt{(p_2)^{-1}}}}^{ \mt{(P_2)^{-1}}}\goverbrace{\mtx{\mt{D_1}&\mt{X_1}\\\mt{0}&\mt{M_1}}}^{\mt{(P_1)^{-1}MP_1}}\goverbrace{\mtx[cc]{\mt{I}&\mt{0}\\\mt{0}&\mt{p_2}}}^{\mt{P_2}} =\mtx{\mt{D_1}&\mt{X_1p_2}\\ \mt{0}&\mt{(p_2)^{-1}M_1p_2}} \end{align} のように相似変換を続ける。
$\mt{(p_2)^{-1}M_1p_2}$が対角化行列になっていれば、行列は上三角行列化されたことになる。そうでなかったなら、話を次にすすめる。$\mt{M_1}$という$(N-k)\times(N-k)$行列も固有ベクトルを1本は持っているはずなので、$\mt{(p_2)^{-1}M_1p_2}=\mtx{\mt{D_2}&\mt{X_2}\\\mt{0}&\mt{M_2}}$の形にはできる（対角化できた部分を増やせる）。
これでもまだ三角化が完了してなかった場合は、$\mt{M_2}$の部分について同じ作業を繰り返せば、いつか、全体が上三角行列になる。
こうしてできた上三角行列の対角成分に$\lambda_1,\lambda_2,\cdots,\lambda_k$があることまではすでにわかっている。残りの$N-k$個が$\lambda'_{k+1},\cdots,\lambda'_\sN$だったとして、$\mt{M}-\xcol{x}\mt{I}$を相似変換した行列（対角成分は$\lambda_i-\xcol{x}$と$\lambda'_i-\xcol{x}$）の行列式を計算すると、
\begin{align}
\det\kakko{\mt{P^{-1}}(\mt{M}-\xcol{x}\mt{I})\mt{P}}
=\prod_{\dum{i}=1}^k (\lambda_{\dum{i}}-\xcol{x})\times
\prod_{\dum[ycolor]{j}=k+1}^N(\lambda'_{\dum[ycolor]{j}}-\xcol{x})
\end{align}
となる（三角行列の$\det$には対角成分以外は寄与しない）。相似変換は行列式を変えないはずだから、これは固有多項式に一致しなくてはいけない。つまり$\mt{P^{-1}MP}$の対角成分にはもともとの行列$\mt{M}$の固有値が重複度の回数ずつ現れる。ここで$\mt{P^{-1}NP}$が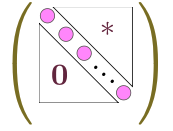
の形になったことを考えると、$\mt{P^{-1}} \phi_{\mt{M}}\kakko{\mt{M}}\mt{P}$は
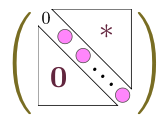
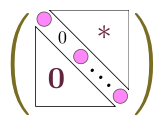
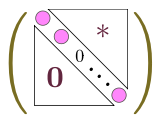$\cdots$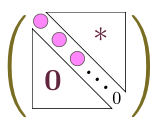
のようになり、この行列の積は0になる。
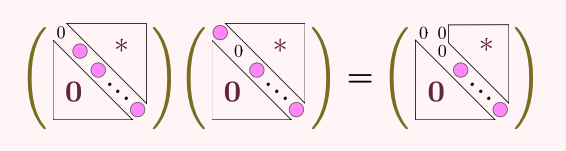
のように、「1列めと2列めが全て0になった行列」になる。
その次と掛け算すると今度は3列めも消える。
以下同様に考えていくと、上の式の計算が終わると全ての行が消える。
こうして、Cayley-Hamiltonの定理が対角化できない場合でも証明された。
任意の行列$\mt{M}$は適当な正則行列$\mt{P}$を使って上三角行列の形に相似変換することができる。この結果の上三角行列の対角成分には、特性方程式の解がそれぞれの重複度の回数ずつ登場する。
も同時に示された。
特性方程式の解が重複している場合にどのようなことが起こるのかについて考えるため、次の節で「一般化固有ベクトル」とそれによるベクトル空間の分解を考えよう。