ここでベクトルの定義を、図形を離れてやり直そう。
$N$次元のベクトルとは実数を$N$個並べたものである(ただそれだけではなく、以下に示す演算の規則が満たされているものをベクトルと呼ぶ)。
まずは\文中式{$N=3$}の場合を考えよう。$\mtx[ccc]{\xcol{x}&\ycol{y}&\zcol{z}}$または$\mtx[c]{\xcol{x}\\[-1mm] \ycol{y}\\[-1mm] \zcol{z}}$のように「$\xcol{x}$成分、$\ycol{y}$成分、$\zcol{z}$成分」(各成分の名前はどうでもよい)と並べて表現する。前節で図形から定義した空間内のベクトル$\vec v$を$\xcol{x},\ycol{y},\zcol{z}$軸方向の基底ベクトルの線形結合として表現すると$v_x\ve_x+v_y\ve_y+v_z\ve_z$のようになるが、これと三つの数字を並べたベクトルとしてのベクトル$\mtx[c]{v_x\\[-1mm]v_y\\[-1mm]v_z}$が対応していることになる。しかし、数ベクトルは特に「矢印」のような図形的定義がなくても書き下すことができるので、こっちの方が「広い」のである。実際、これから先で使うことになる「ベクトル」は平面や空間内で定義されたものとは限らない。これまでに出てきた例でも、$\mtx[c]{りんごの数\\バナナの数}$というのは立派なベクトルなのだ(矢印ではないけれど)。
ベクトルを$\mtx[c]{a_x\\[-1mm]a_y\\[-1mm]a_z}$のように縦に並べるのを「列ベクトル(column vector)」(または「縦ベクトル」)、$\mtx[ccc]{a_x&a_y&a_z}$のように横に並べるのを「行ベクトル(raw vector)」(または「横ベクトル」)と呼ぶ。行と列のどっちが行でどっちが列かわからなくなる、という人は漢字 を思い出そう。横線を含む漢字が「行」で、縦線を含む漢字が「列」である。
を思い出そう。横線を含む漢字が「行」で、縦線を含む漢字が「列」である。
本講義では、ベクトルは主に$\mtx{a&b\\[-1mm]c&d}\mtx[c]{v_x\\[-1mm] v_y}$のように「行列が掛かる相手」として登場するので、縦ベクトルを基本にし、ベクトルを一文字で$\vec v$と表すときは縦ベクトルだとする。よって$\vec v=\mtx[c]{v_x\\[-1mm]v_y}$}と書く。なお、$\vec v$と書いたときは表現をどのようにするかを指定してない、抽象的なベクトルであり、$\mtx[c]{v_x\\[-1mm]v_y}$と書いたときはある表現を指定した上で(つまり、$x$成分とか$y$成分とは何であるかを指定した上で)「$x$成分は$v_x$、$y$成分は$v_y$」と示している。よってこの二つは数式を書くときの「文脈」が違うので、等号で結ぶのは厳密には正しくない、と言う立場もある。ここでは細かいことは言わずに$=$で書いてしまった。
行列やベクトルの「縦$\leftrightarrow$横」の取り替える操作を「転置(transpose)」と呼び、横ベクトルは「縦ベクトルを転置(transpose)したもの」と解釈する。転置を記号${}^t$を右に付けることで表現するので、$(\vec v)^t=\mtx[cc]{v_x & v_y}$である。
実数の足算(加法)と掛算(乗法)については以下のような法則が成り立つ。
実数の和の満たす法則
\begin{equation}
\begin{array}{rl}
交換法則:&a+b=b+a\\
結合法則:&(a+b)+c=a+(b+c)\\
分配法則:&a(b+c)=ab+ac
\end{array}
\end{equation}
ベクトルの和と実数倍に関しても以下が成立する。
ベクトルの和と実数倍の満たす法則
\begin{equation}
\begin{array}{rl}
交換法則:&\vec a+\vec b=\vec b+\vec a\\
結合法則:&(\vec a+\vec b)+\vec c=\vec a+(\vec b+\vec c)\\
ベクトル和の分配法則:&\lambda(\vec a+\vec b)=\lambda\vec a+\lambda\vec b\\
スカラー和の分配法則:&(\lambda_1+\lambda_2)\vec a=\lambda_1\vec a+\lambda_2\vec a
\end{array}
\end{equation}
ここで、通常の数を「スカラー」と呼んでいる。今の場合は実数である(複素数に拡張したりする話は、後でやる)。これらの法則は図を描いて確認することができるだろう。
以下は$\alpha,\beta$およびベクトルの成分が実数の場合を考えよう。
ベクトルは成分を並べて$\vec a=\mtx[c]{a_x,a_y}$と表現してもよい。これを「成分表示」と呼ぶ。こうして分解すると、
\begin{equation}
\begin{array}{rl}
\vec a+\vec b=&a_x\ve_x+a_y\ve_y+b_x\ve_x+b_y\ve_y\\
=&(a_x+b_x)\ve_x+(a_y+b_y)\ve_y
\end{array}
\end{equation}
となり、ベクトルの足算は成分をそれぞれ足算すればよい。成分表示で書くと上の式は
\begin{equation}
\mtx[c]{a_x\\a_y}+\mtx[c]{b_x\\b_y}=\mtx[c]{a_x+b_x\\a_y+b_y}
\end{equation}
である。ベクトルから$\xcol{x}$成分と$\ycol{y}$成分を求める方法については、後で考えよう。
ベクトルを成分で表現したときの引算は
\begin{equation}
\begin{array}{rl}
\vec a-\vec b=&a_x\ve_x+a_y\ve_y-b_x\ve_x-b_y\ve_y\\
=&(a_x-b_x)\ve_x+(a_y-b_y)\ve_y\\
&または\\
\mtx[c]{a_x\\a_y}-\mtx[c]{b_x\\b_y}=&\mtx[c]{a_x-b_x\\a_y-b_y}
\end{array}
\end{equation}
のように成分どうしで引算をすればよい。
ベクトルの線形結合を作るという操作は
\begin{align}
\goverbrace{\mtx[c]{V_x\\ V_y}}^{\vec V}
=\alpha\goverbrace{\mtx[c]{a_x\\ a_y}}^{\vec a}+\beta\goverbrace{\mtx[c]{b_x\\ b_y}}^{\vec v}
=\mtx[c]{\alpha a_x+\beta b_y\\ \alpha a_y+\beta b_y}
\end{align}
と書くことができる。実はこれは、
\begin{align}
\mtx[c]{V_x\\ V_y}=\mtx[cc]{a_x&b_x\\ a_y&b_y}\mtx[c]{\alpha\\ \beta}
\end{align}
という行列計算とやっていることは同じである。ここに現れた行列$\mtx[cc]{a_x&b_x\\ a_y&b_y}$は、$\mtx[cc]{\tatevec{\begin{array}{c}a_x\\a_y\end{array}}&\tatevec{\begin{array}{c}b_x\\b_y\end{array}}}$のように縦ベクトルを二つ並べたものと考えることができる。
以下はベクトルの満たす法則を説明したビデオ
線形独立と線形従属
$k$個のベクトル$\vec a_i=(\vec a_1,\vec a_2,\cdots\vec a_k)$があって、どんな0ではない係数$ \alpha_i$を持ってきて線形結合を作っても0ベクトルにできないとき、つまり
\begin{align}
\sum_{i=1}^k
\alpha_i\vec a_i=
\alpha_1\vec a_1+\alpha_2\vec a_2+\cdots+\alpha_k\vec a_k
=\vec 0
\end{align}
となるのは全ての$\alpha_i$が0である場合だけであるとき、この$k$個のベクトル$\vec a_i$は「線形独立(linearly independent)」または「一次独立」だと言う。逆に、適当に係数$\allc{\alpha_*}$をもってくれば上の式が成り立つようにできるとき、これらのベクトル$\allc{{\vec v}_*}$は「線形従属(linearly dependent)」または「一次従属」だと言う。
平面のベクトルの場合、2本のベクトル$\vec a,\vec b$が同じ方向を向いてなければ線形独立である。同じ方向を向いていれば、$\vec a=k\vec b$($k$はある定数)が成り立つということで、この場合$\vec a,\vec b$は線形従属である。以上は図形のベクトルの経験から納得できるだろう。数ベクトルで同じことを考えると、ベクトル$\mtx[c]{a_x\\[-1mm]a_y}$と$\mtx[c]{b_x\\[-1mm]b_y}$を考えて
\begin{align}
\alpha\mtx[c]{a_x\\a_y}+\beta\mtx[c]{b_x\\b_y}\stackrel{?}{=}\mtx[c]{0\\0}
\end{align}
で等号が成り立つようにしようとすると、$\alpha a_x+\beta b_x=0$にしなくてはいけないから$\beta=-{\alpha a_x\over b_x}$と決まってしまう。すると、
\begin{align}
\alpha\mtx[c]{a_x\\a_y}-{\alpha a_x\over b_x}\mtx[c]{b_x\\b_y}
= \mtx[c]{0\\\alpha a_y-{\alpha a_x\over b_x}b_y}
= \mtx[c]{0\\\alpha \left(
a_y-{a_x\over b_x}b_y
\right)}
\end{align}
となるが、$a_y-{a_x\over b_x}b_y=0$が成り立たないと右辺は零ベクトルにならない。この条件は${a_x\over b_x}={a_y\over b_y}=k$と書き直すことができるから、つまりは$\vec a$が$\vec b$の定数倍(今の場合は$k$倍)であるときには(そのときに限り)線形従属である。
$N$次元のベクトルの$k$本の線形結合$\alpha_1\vec v_1+\alpha_2\vec v_2+\cdots \alpha_k\vec v_k$は行列を使って表現すると
\begin{align}
\mtx[cccc]{\tatevec{\begin{array}{c}\\\vec v_1\\ \\\end{array}}&\tatevec{\begin{array}{c}\\\vec v_2\\ \\\end{array}}&\cdots&\tatevec{\begin{array}{c}\\\vec v_k\\ \\\end{array}}}\mtx[c]{\alpha_1\\\alpha_2\\\vdots\\\alpha_k}
\end{align}
と書くことができる。このベクトル$\allc{{\vec v}_*}$が線形従属なら、上の式の計算結果が$\vec 0$になることがある。線形従属かどうかを判定するにはどうすればよいかというと、この行列の性質を調べればよい。その性質とはなにかについては、後でじっくり説明しよう。
3次元以上については線形従属の条件は単純に「定数倍」とはならない(たとえば、3本のベクトルが互いに平行ではないが\文中式{$\vec a+\vec b+\vec c=0$}になっている状況は考えられる)。$N$次元のベクトル空間では、線形独立なベクトルは$N$個しかない。定義から、$N$次元なら任意のベクトルを(基底を$\vec v_1,\vec v_2,\cdots,\vec v_N$として)$\vec V=\alpha_1\vec v_1+\alpha_2\vec v_2+\cdots \alpha_N\vec v_N$と表すことができる($\alpha_1,\alpha_2,\cdots,\alpha_N$は適切に選ばれた係数)。
シラバスの予定では内積までやるところでしたが、内積・外積の話は来週に回します。
以上で第2回の授業は終わりです。webclassへ行って、「第2回授業感想・コメントシート」に答えてください。出席の代わりです(この授業は出席点はありませんが、皆さんがどの程度受講しているかも確認したいのと、反応もみたいので)。
物理数学I webclass
この感想・コメントシートに書かれたことについては、代表的なものに対しては次のページで返答します。
なお、webClassに情報を載せていますが、授業があった日の午後7時より約1時間、オンラインオフィスアワーとしてzoomを開いてます。質問や相談などがある人は来て話してください。
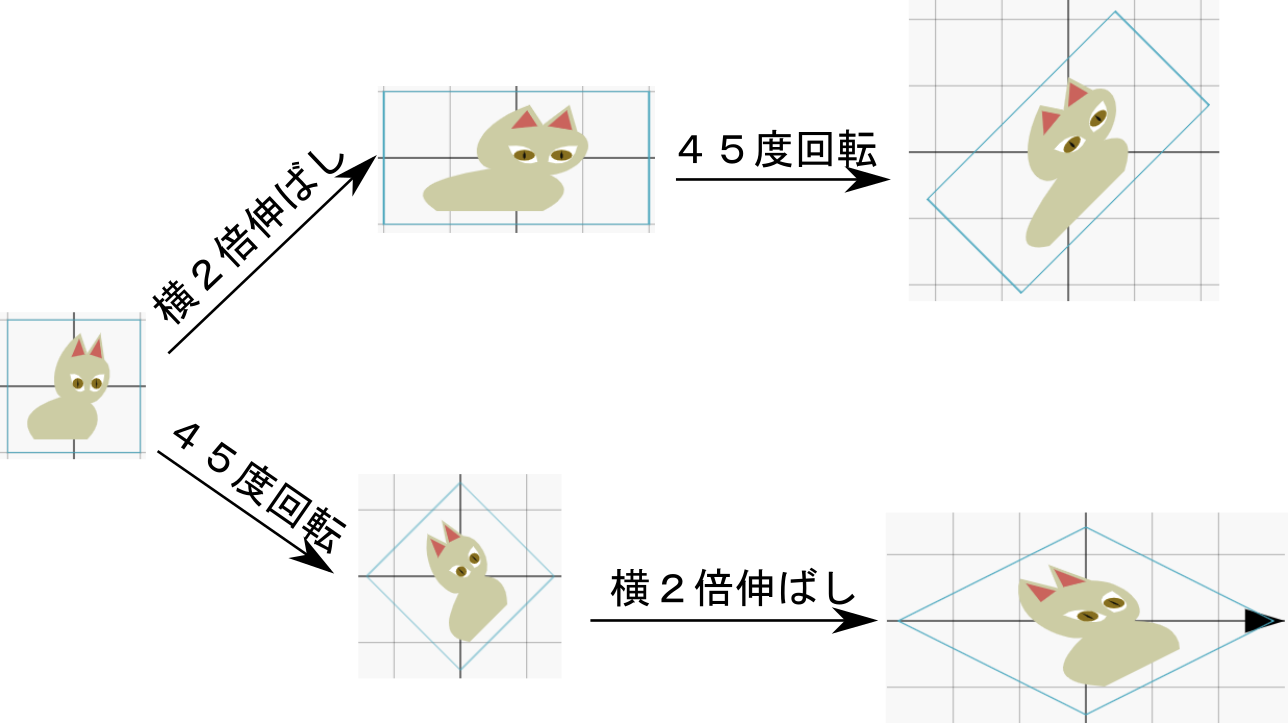
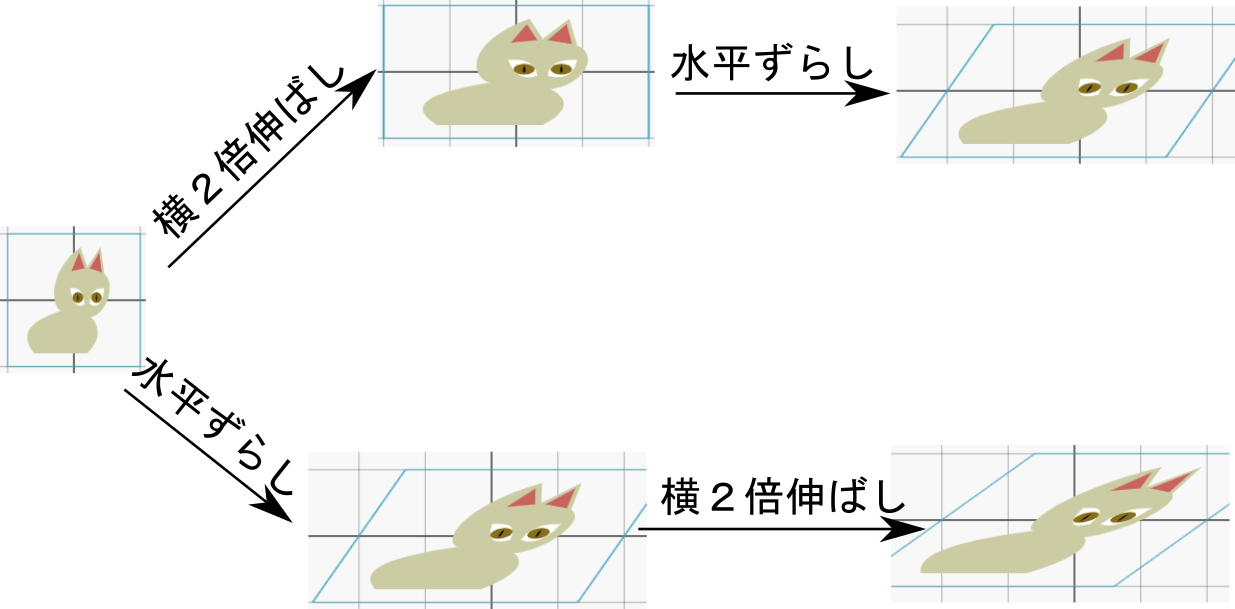
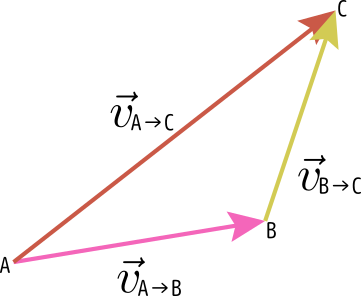
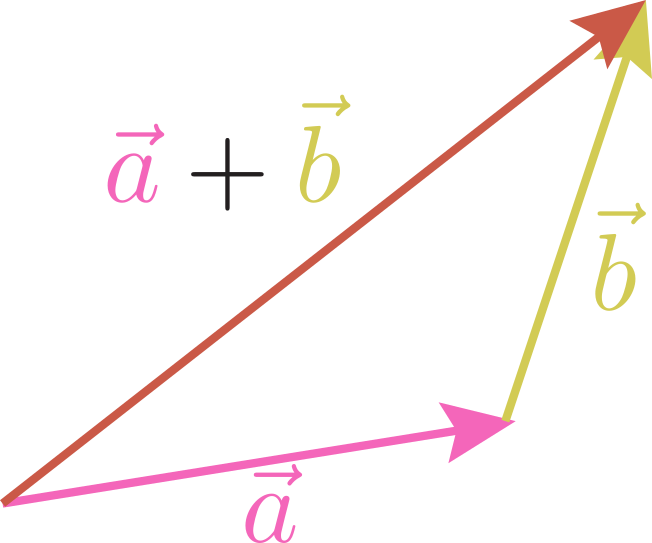 のように「ベクトルの和の規則」を定める。
のように「ベクトルの和の規則」を定める。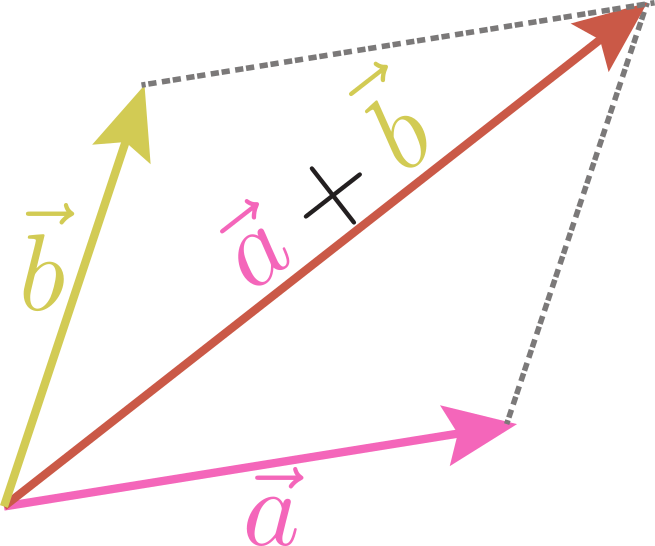 のような操作だと考えてもよい。このベクトルの足し算のやり方を「平行四辺形の法則」などと呼ぶ。
のような操作だと考えてもよい。このベクトルの足し算のやり方を「平行四辺形の法則」などと呼ぶ。

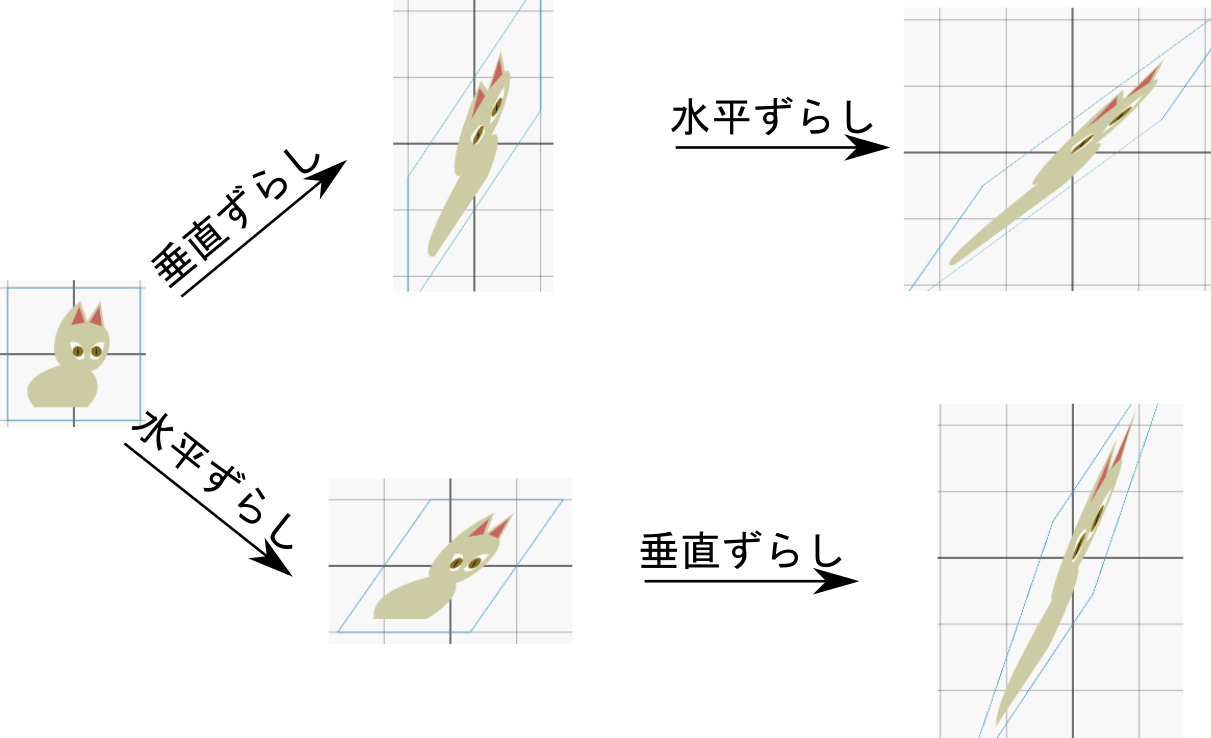
 のように図を描くことで、「ベクトルを2倍する」とは「向きを変えずに長さを2倍にする」ことだとわかる。同様に「3倍」「4倍」を順に定義していけば、「ベクトルの整数倍」という演算が定義できる。この逆を考えて${1\over2}\vec a+{1\over 2}\vec a=\vec a$が成り立つように「${1\over 2}$倍」「${1\over 3}$倍」を順に定義することで「ベクトルの${1\over 整数}$倍」が定義される。こうやって拡張していけば、任意の有理数$\lambda$に関して「ベクトルを$\lambda$倍する」とは「向きを変えずに長さを$\lambda$倍にする」としよう。ここまでくれば$\lambda$が任意の実数に対してこの定義を使ってよいだろう。
のように図を描くことで、「ベクトルを2倍する」とは「向きを変えずに長さを2倍にする」ことだとわかる。同様に「3倍」「4倍」を順に定義していけば、「ベクトルの整数倍」という演算が定義できる。この逆を考えて${1\over2}\vec a+{1\over 2}\vec a=\vec a$が成り立つように「${1\over 2}$倍」「${1\over 3}$倍」を順に定義することで「ベクトルの${1\over 整数}$倍」が定義される。こうやって拡張していけば、任意の有理数$\lambda$に関して「ベクトルを$\lambda$倍する」とは「向きを変えずに長さを$\lambda$倍にする」としよう。ここまでくれば$\lambda$が任意の実数に対してこの定義を使ってよいだろう。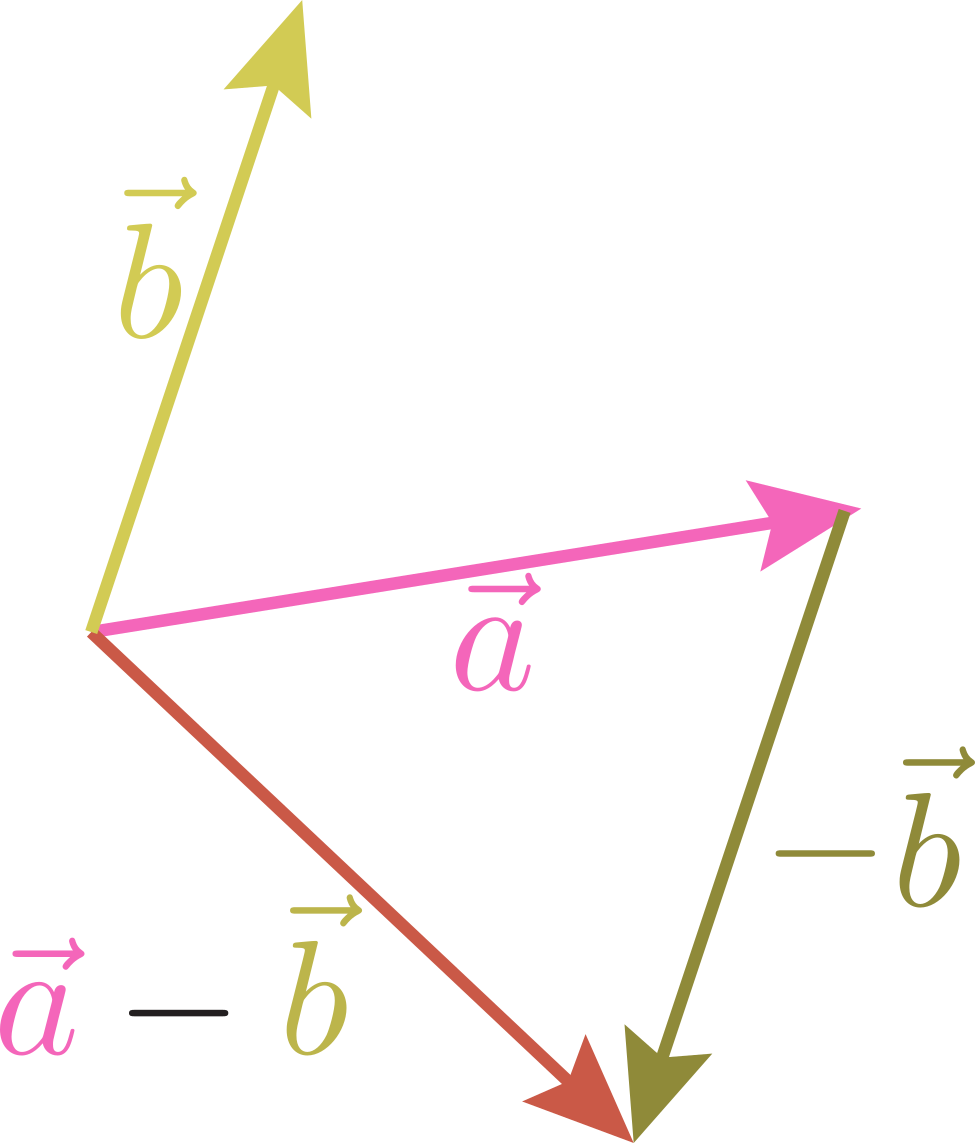 のように「逆向きにしてから足す」と考えてもよいし、
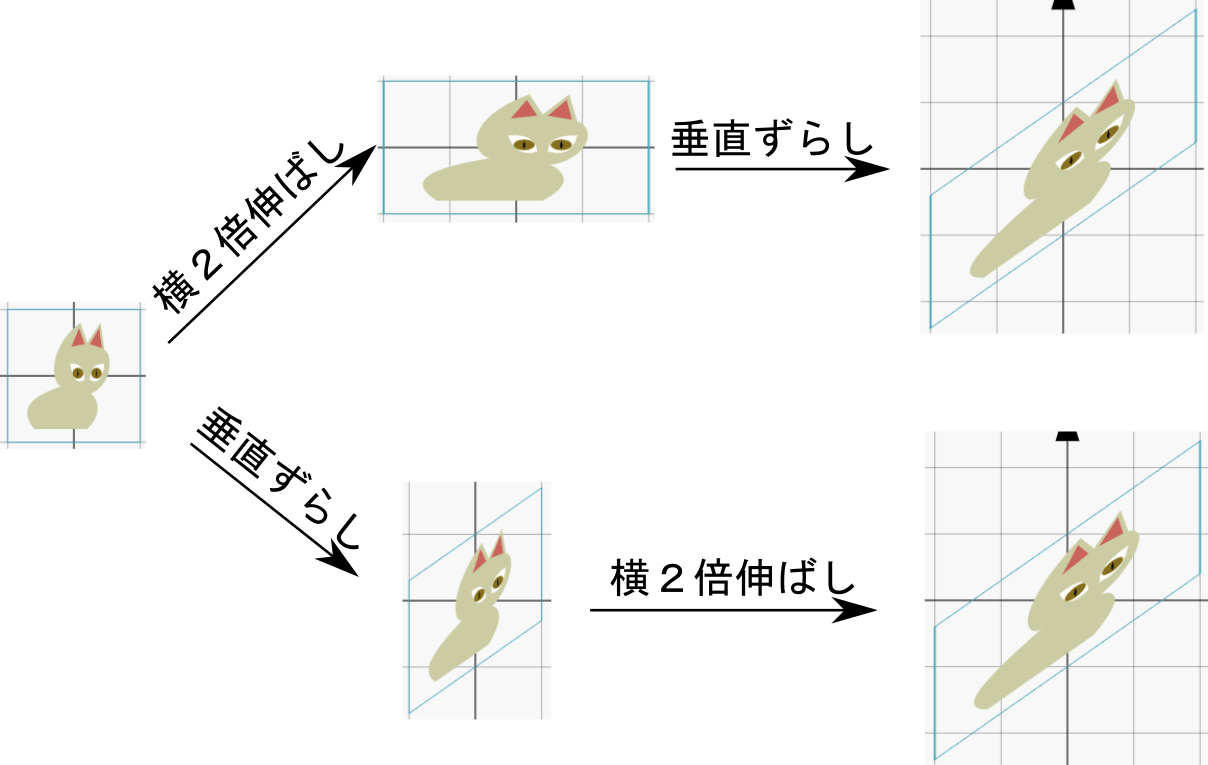
のように「逆向きにしてから足す」と考えてもよいし、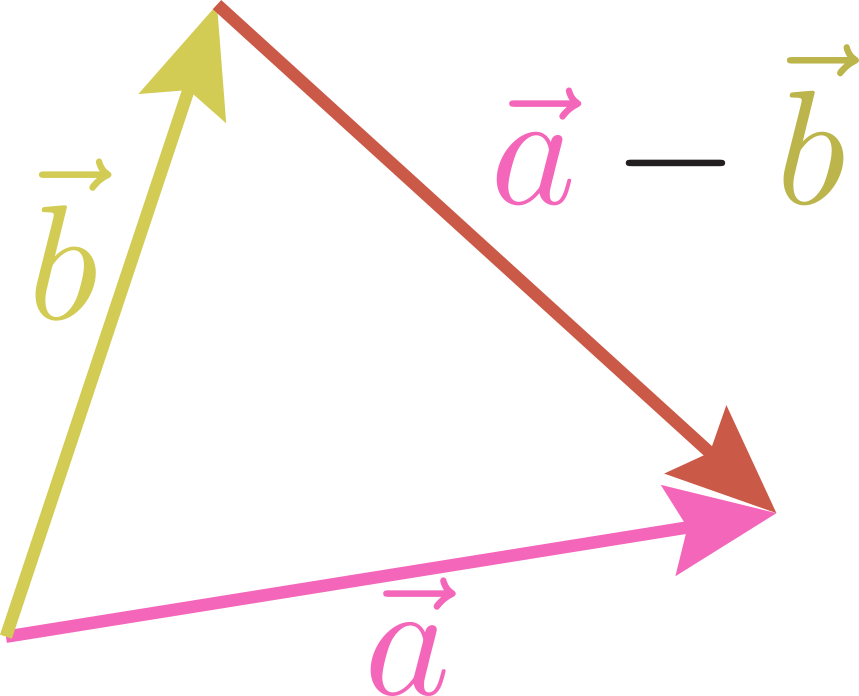 のように「
のように「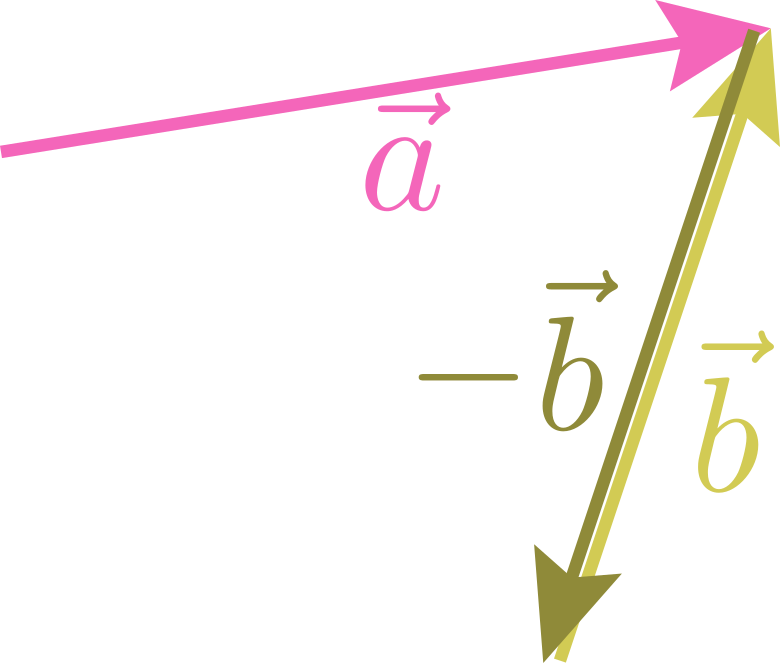 のように「行って戻る」ことで打ち消すと考えればよい。
のように「行って戻る」ことで打ち消すと考えればよい。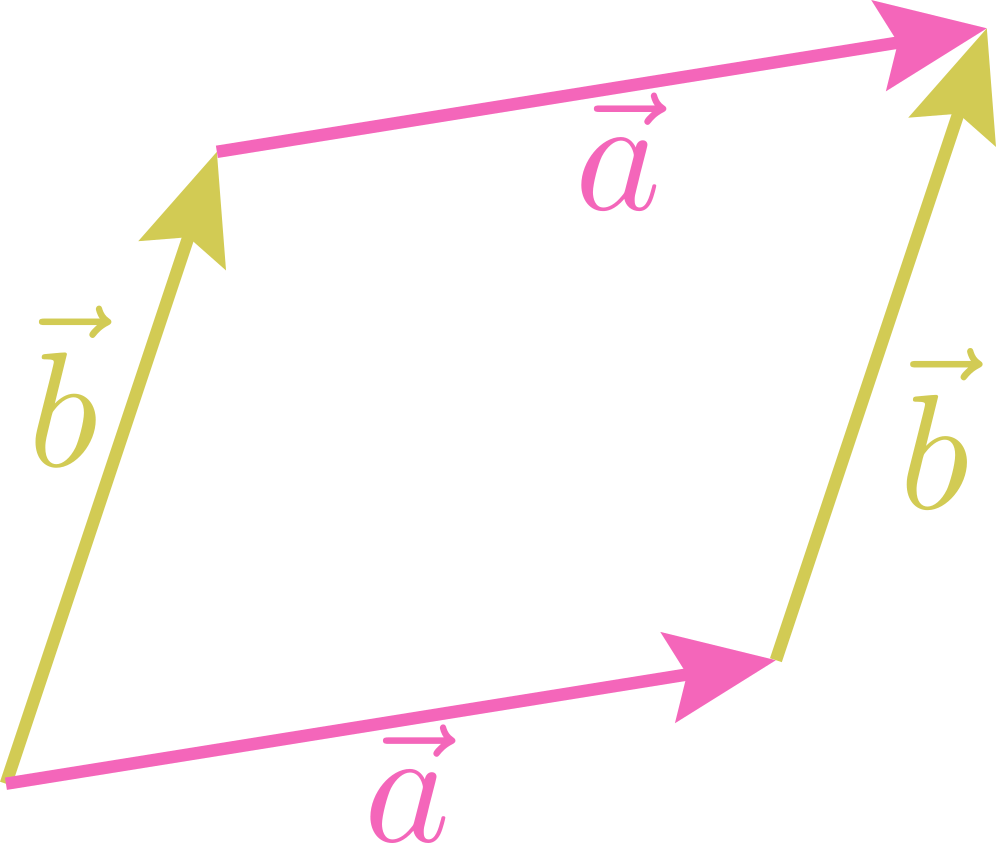 のように「根本も先も動かせば、平行移動したのと同じ(何も変わってない)」から打ち消すことになると考えればよい。
のように「根本も先も動かせば、平行移動したのと同じ(何も変わってない)」から打ち消すことになると考えればよい。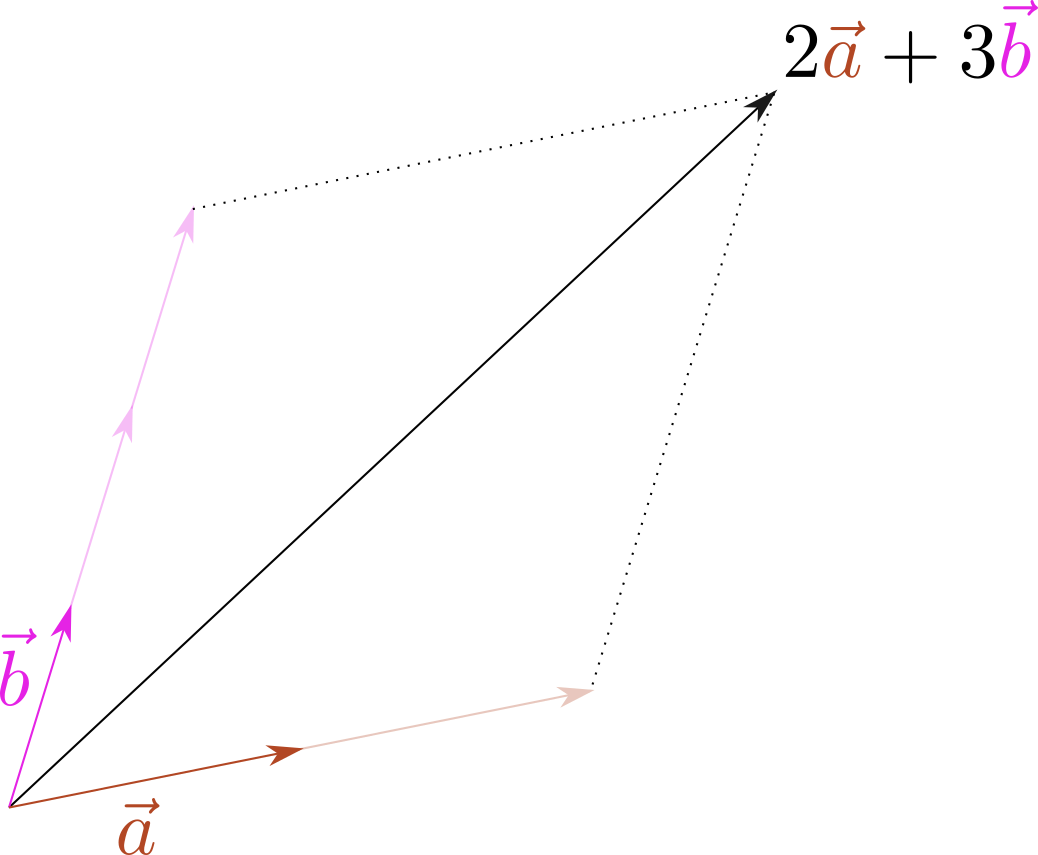
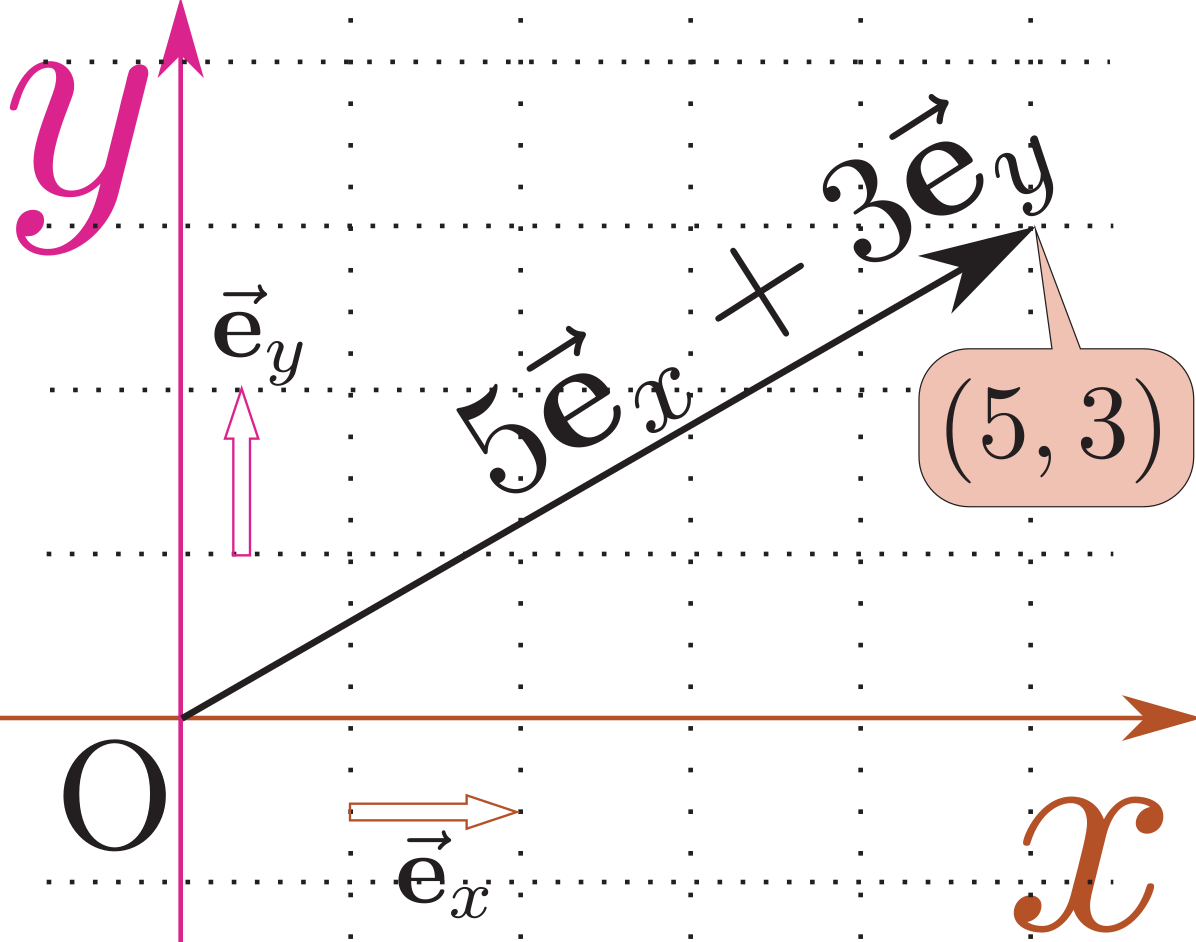
 を思い出そう。横線を含む漢字が「行」で、縦線を含む漢字が「列」である。
を思い出そう。横線を含む漢字が「行」で、縦線を含む漢字が「列」である。