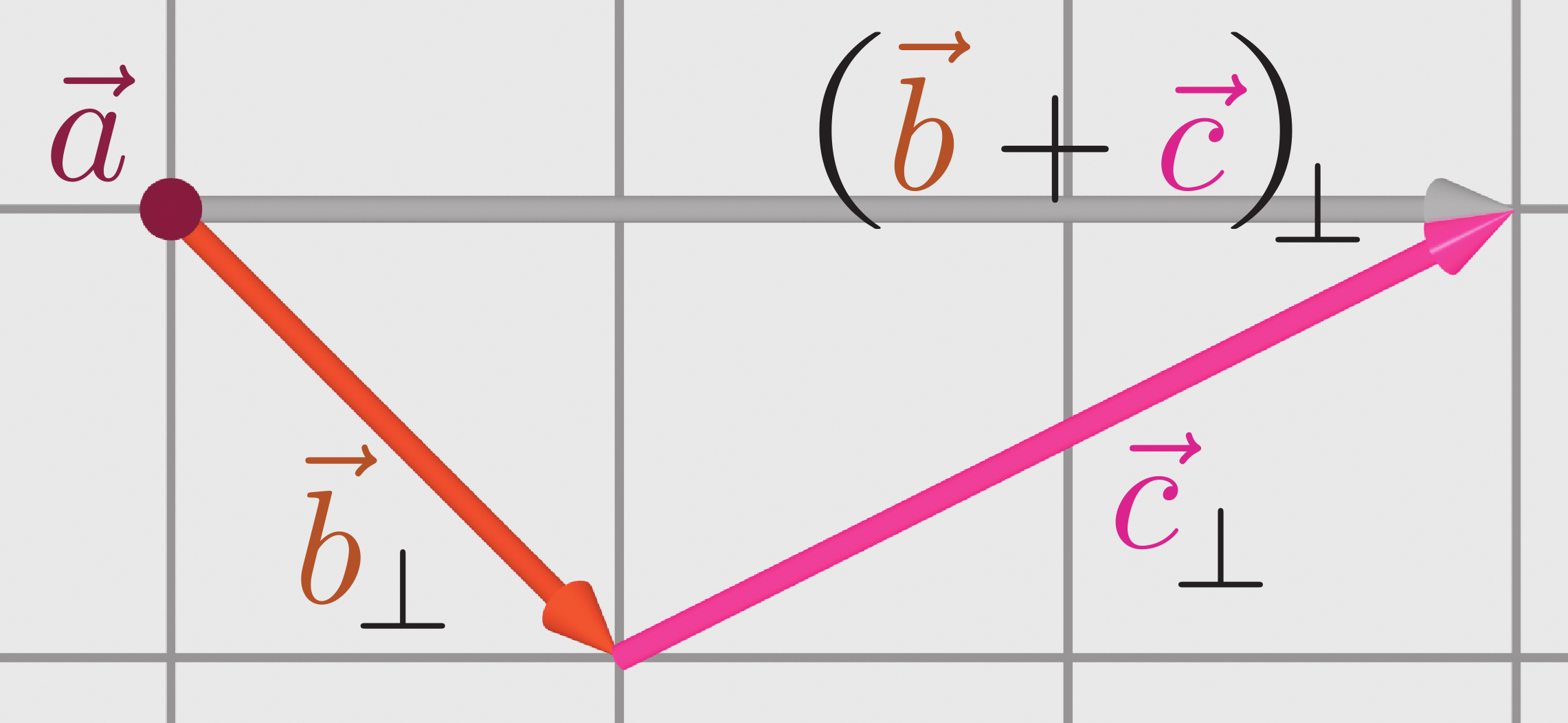外積に関する定理などの説明ビデオ↓
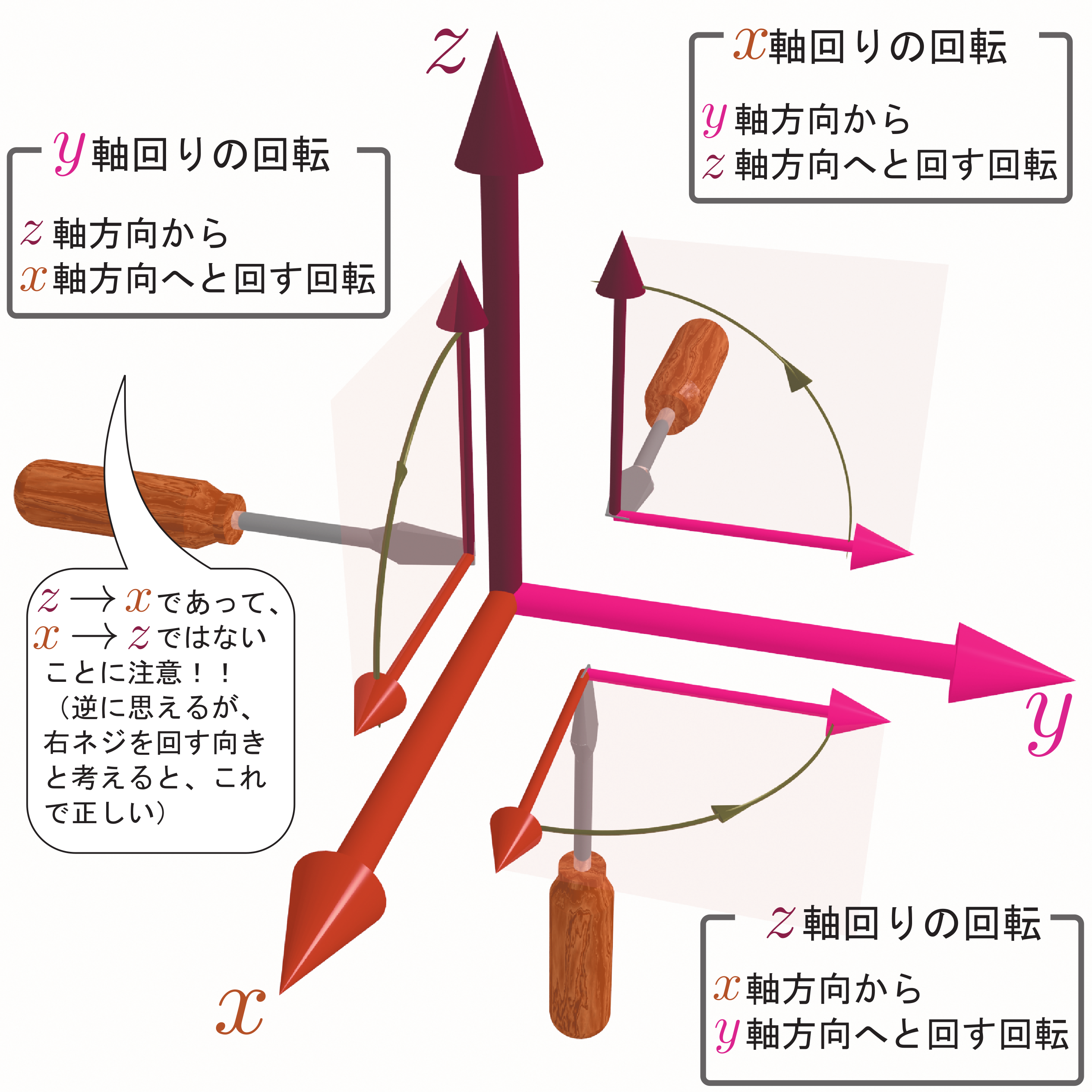
3次元のベクトルの場合、
\begin{equation}
\begin{array}{ll}
\\
\ve_x\times\ve_y=\ve_z,~~~
& \ve_y\times\ve_x=-\ve_z,\\
\ve_y\times\ve_z=\ve_x,~~~
& \ve_z\times\ve_y=-\ve_x,\\
\ve_z\times\ve_x=\ve_y,~~~
& \ve_x\times\ve_z=-\ve_y
\end{array}
\label{cycliceq}
\end{equation}
という関係になる。
これらの式は1行目の式をサイクリック置換すれば他の式も得られるようになっている。
「$x$を$y$に、$y$を$z$に、$z$を$x$に」という変更

を「サイクリック置換」と呼ぶ。
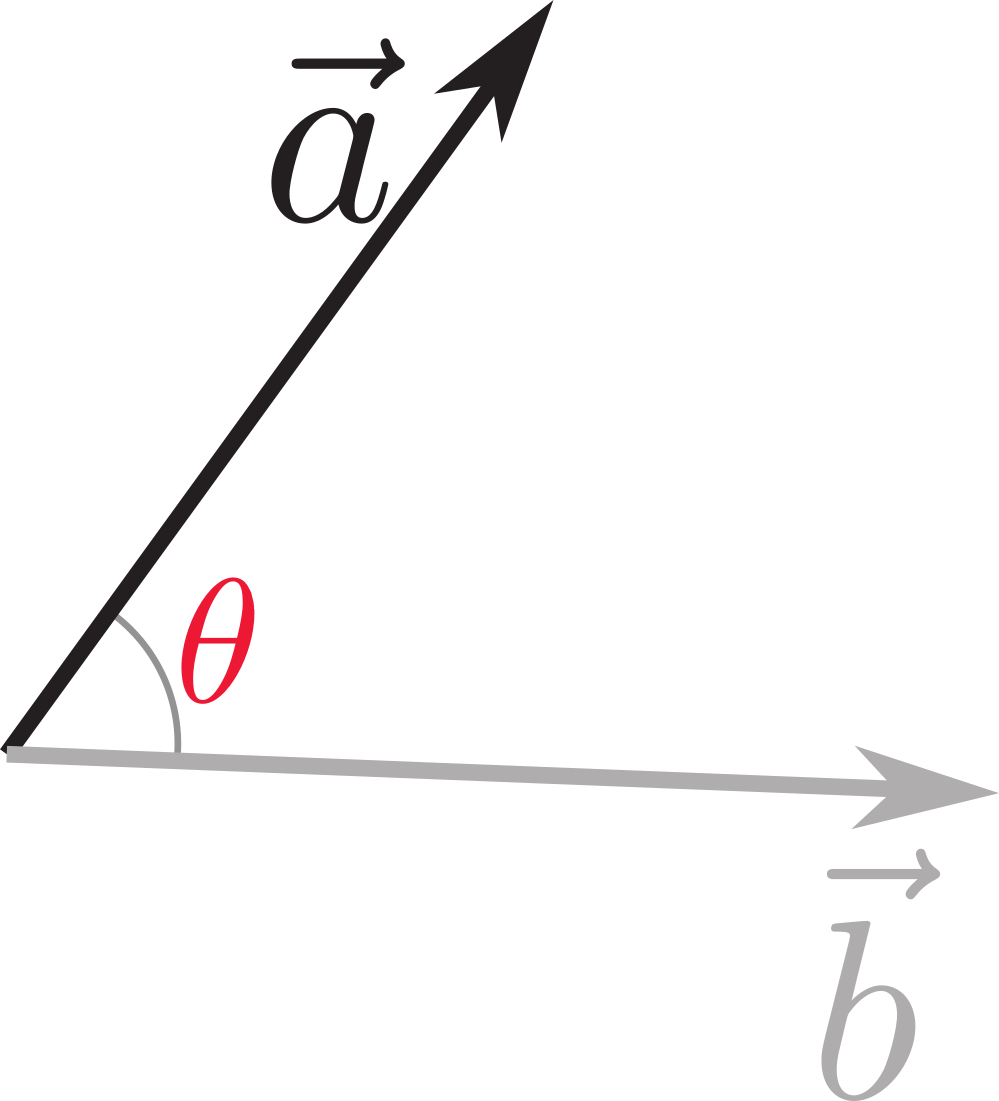
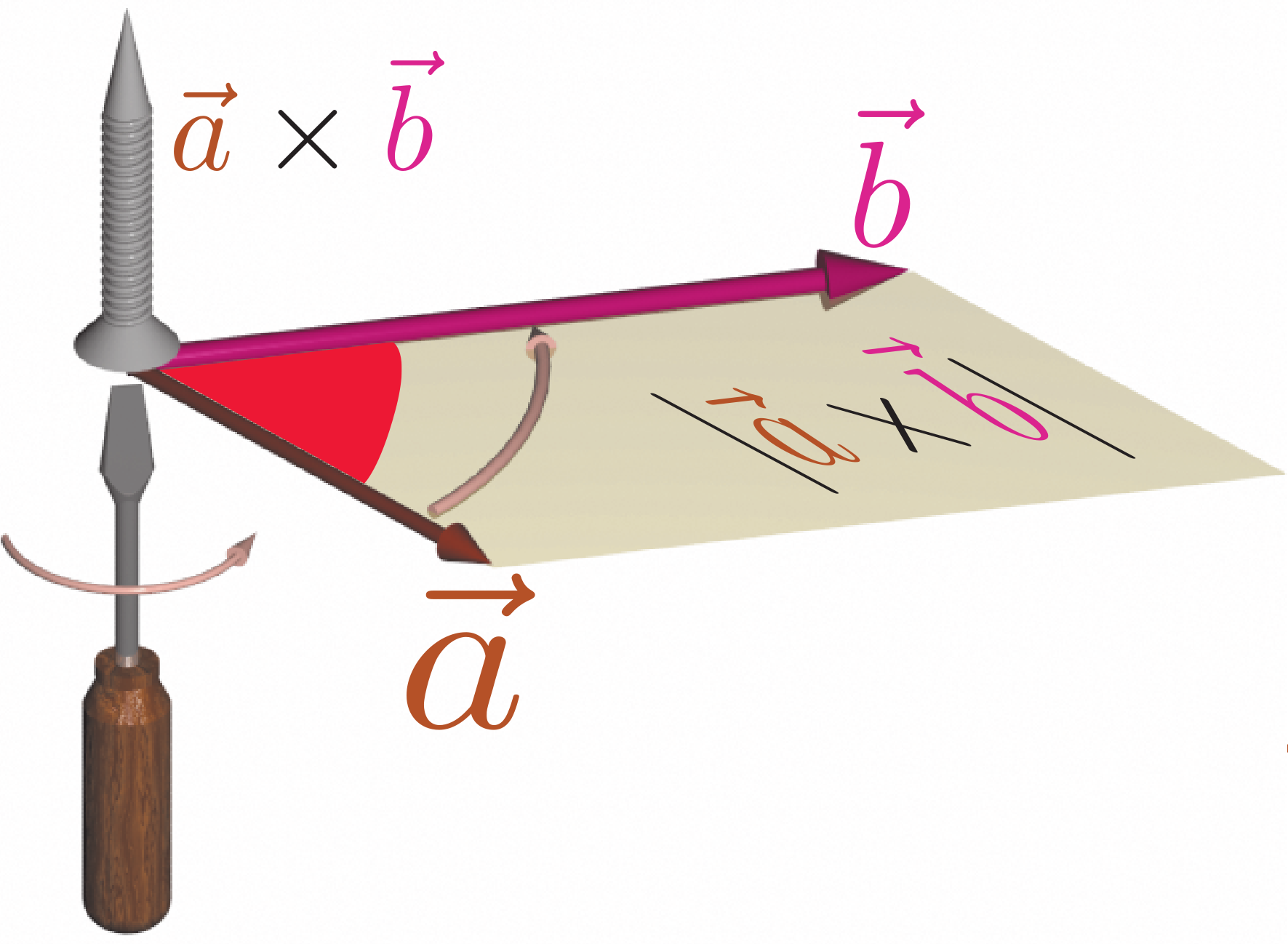
同じ方向を向いているベクトルどうしの外積は0である。平行四辺形の面積という意味を考えれば、「同じ方向を向いている2本のベクトルの作る面積は0」ということから納得できる(数式で考えるならば$\theta=0$である)。特に$\xcol{\vec a}\times\ycol{\vec b}=\vec 0$であっても$\xcol{\vec a}$も$\ycol{\vec b}$も零ベクトルでない場合があることには注意しよう。
ベクトルの掛算については注意すべきことがたくさんあるが、特に普通の掛算との違いとして「戻せない演算である」ことに注意したい。普通の数の掛算は「$a$を掛ける」後に「$a$で割る」ことで元に戻せる($a=0$の場合は除く)。しかし外積は(内積も)そうはいかない。そもそも外積に対応する「割る」という演算は存在しない。その理由は明白で「違うベクトルなのに$\xcol{\vec a}$と外積を取ると結果が同じになってしまう」、すなわち、
$$
\ycol{\vec b}\times \xcol{\vec a} = \vec c\times \xcol{\vec a}~~~~~
であるが、~~~~
\ycol{\vec b}\neq \vec c
$$
ということが(いくらでも)あり得るのである。この点を忘れると、
$$
\xcol{\vec a}\times(\vec x+\ycol{\vec b})=\xcol{\vec a}\times\vec c~~~~から~~~~
\vec x+\ycol{\vec b}=\vec c
$$
のような間違った計算を「うっかり」やってしまうことになる。
外積の交換・結合・分配法則
外積についても三つの法則が成り立つかどうか考えよう。
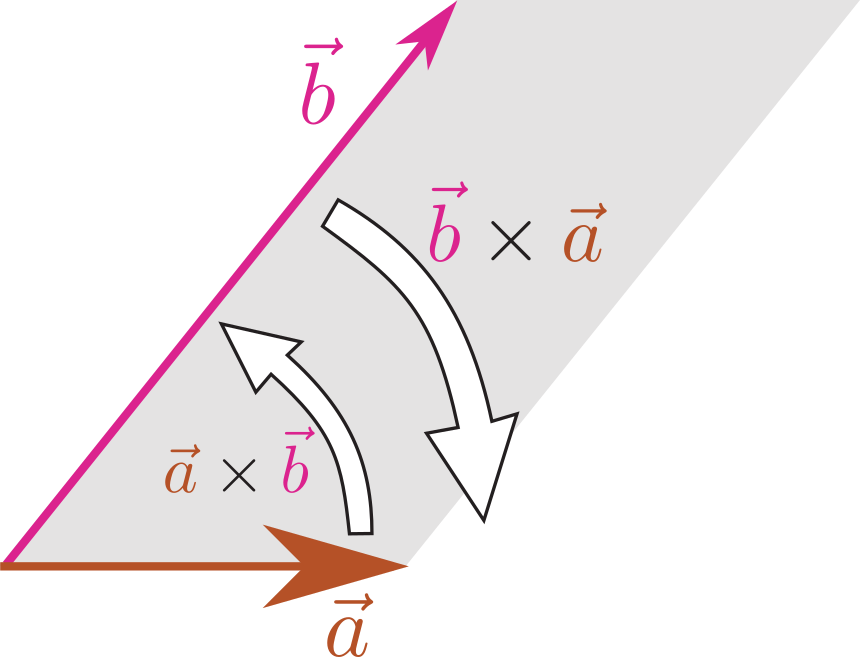
交換法則(成り立たない)
$\xcol{\vec a}\times \ycol{\vec b}$はいわば「$\xcol{\vec a}$というベクトルを$\ycol{\vec b}$の方向に力を加えて回す向き」なのに対し、$\ycol{\vec b}\times \xcol{\vec a}$はその逆で「$\ycol{\vec b}$というベクトルを$\xcol{\vec a}$の方向に力を加えて回す向き」であり、この二つは逆の作用である。
しかし、平行四辺形の面積には違いがないので、絶対値は等しい。よって、
\begin{equation}
\xcol{\vec a}\times\ycol{\vec b}= - \ycol{\vec b}\times \xcol{\vec a}\label{gaisekikoukan}
\end{equation}
が成立する(外積の定義には$\sin \theta$が含まれているが、$\sin (-\theta)=-\sin \theta$からも以上のことはわかる)。3次元では外積の結果のベクトルが逆を向く。
結合法則(意味がない)
2次元の外積は計算結果がスカラーなので$\xcol{\vec a}\times(\ycol{\vec b}\times \zcol{\vec c})$のような計算はできないので結合法則にはそもそも意味がない。
3次元の外積で結合法則は成り立たない例を一つあげておこう(法則が成り立つことを示す時は一つの成り立つ例を出してもダメ(他に成り立たない場合があるかもしれない)であるが、成り立たないことを示すのなら、成り立たない例が一つあればそれで十分)
\begin{equation}
\ve_x \times(\ve_y\times\ve_y)=0
\end{equation}
である(括弧の中の$\ve_y\times\ve_y$が0だから)。一方、
\begin{equation}
(\gunderbrace{\ve_x \times\ve_y}_{=\ve_z})\times\ve_y=\ve_z \times \ve_y = -\ve_x
\end{equation}
となって0ではない。
分配法則(成立する)
分配法則に関しては下のアプリをやってみてください。操作方法は内積のものとほぼ同じなので省略します。終わったら「戻る」で戻ってくること。
アプリは2次元の話なので、3次元の場合も含め、以下で説明しよう。
分配法則は、外積についても成立する。式で書くと
外積の分配法則
\begin{equation}
\zcol{\vec a}\times(\xcol{\vec b}+\ycol{\vec c})=\zcol{\vec a}\times\xcol{\vec b}+\zcol{\vec a}\times \ycol{\vec c}\label{gaisekibunpai}
\end{equation}
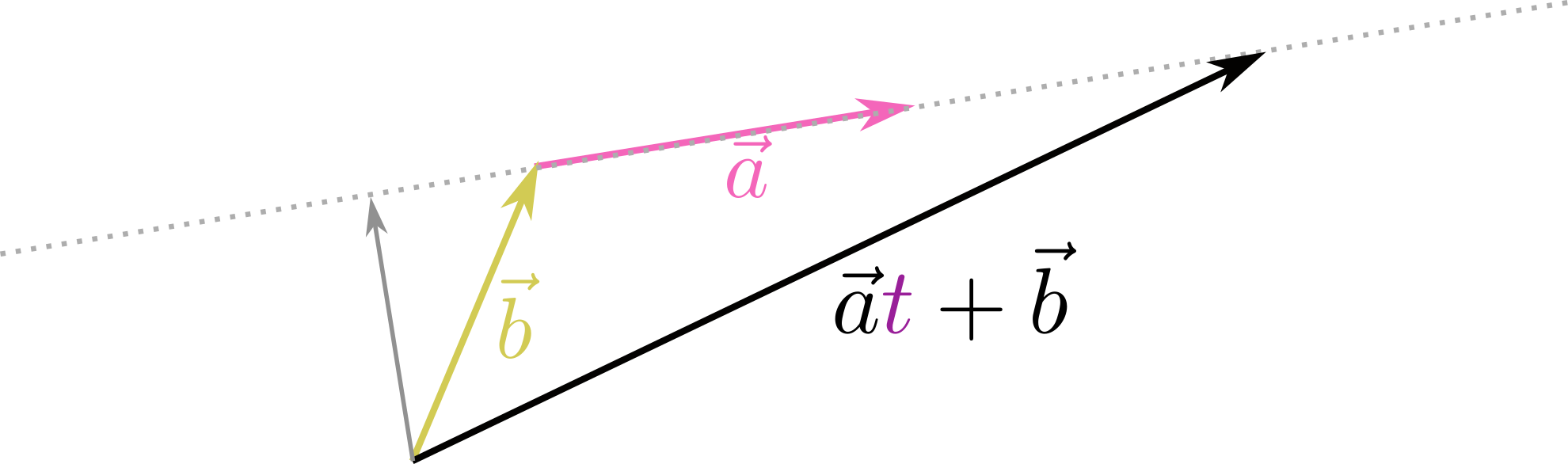
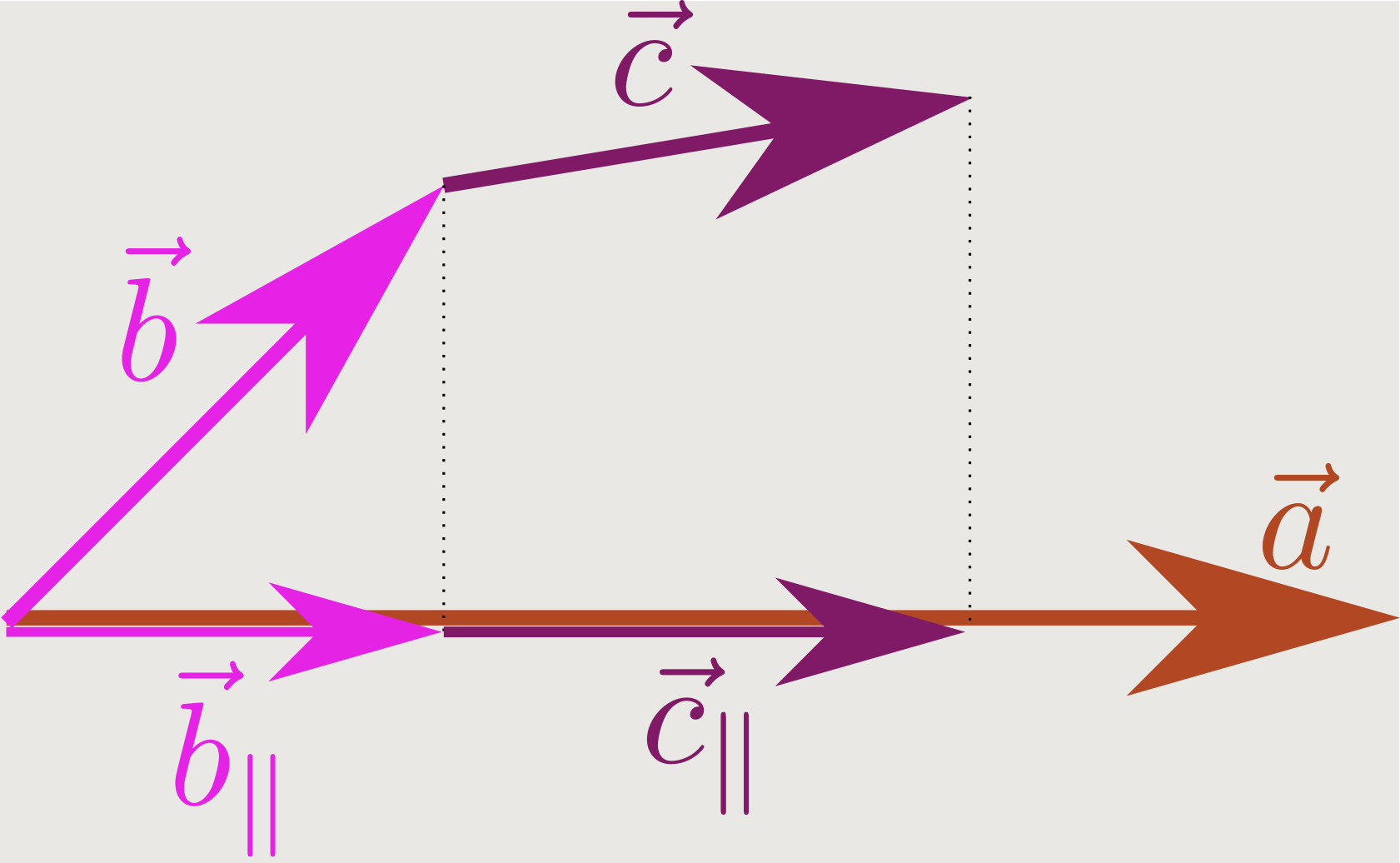
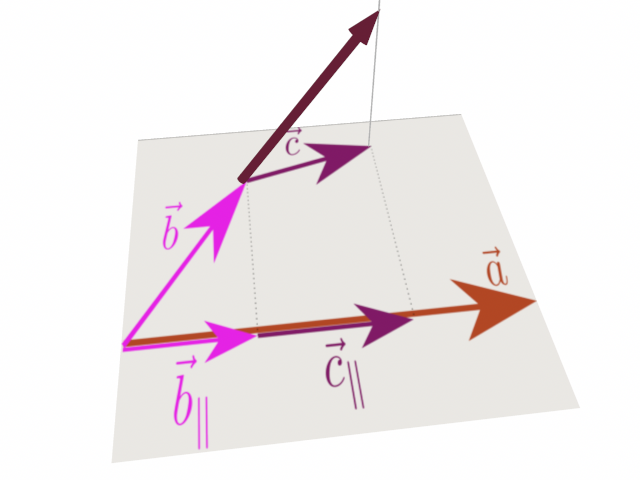
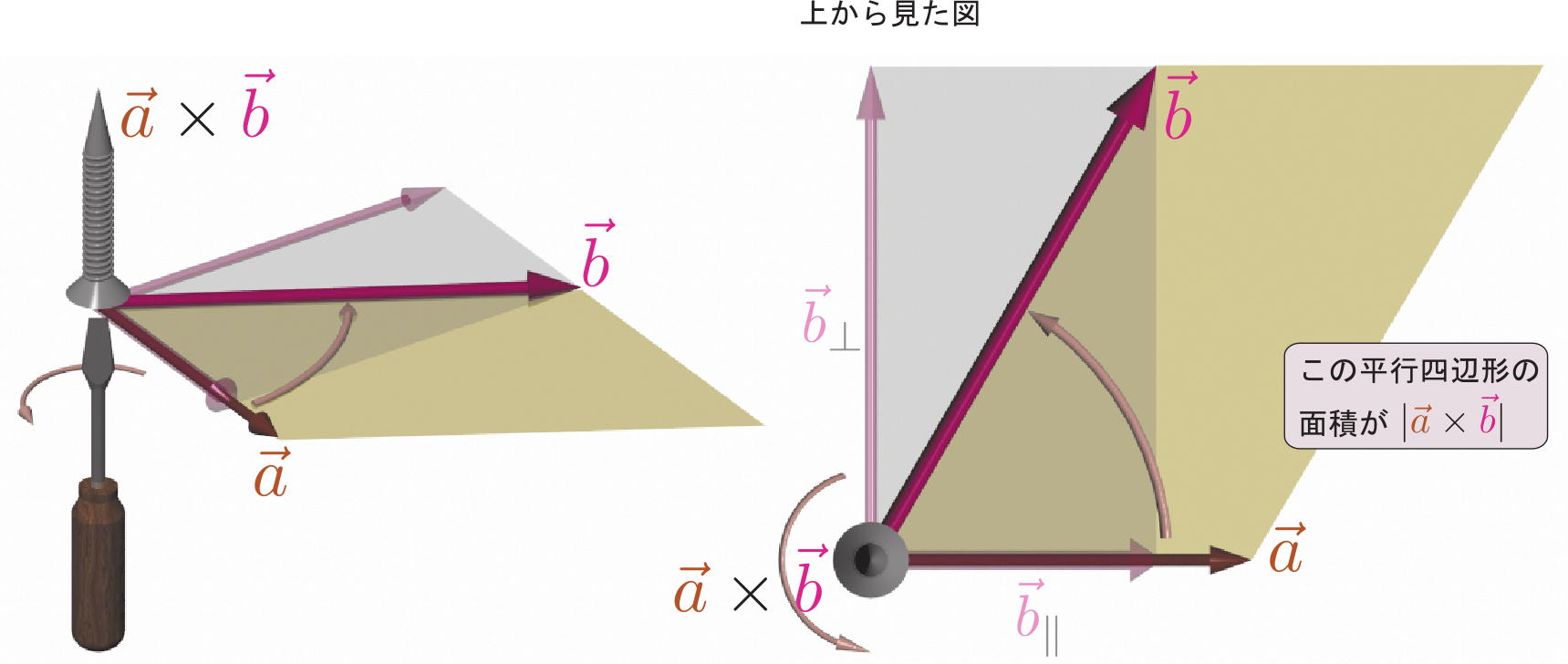
である。三つのベクトルを次の図のように考えよう。
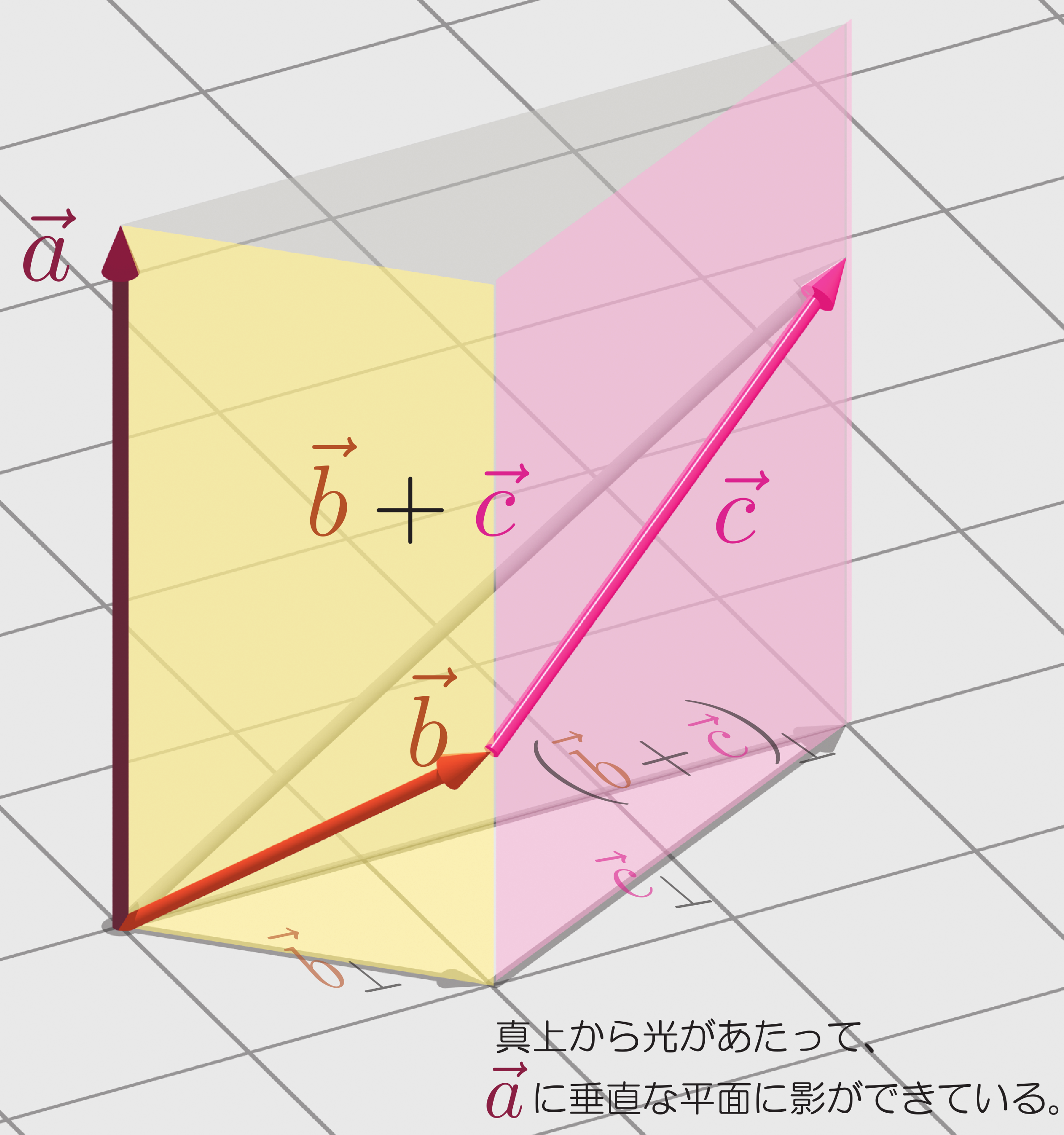
外積を取るときに計算に関与してくるのは$\zcol{\vec a}$に垂直な成分のみであるから、図に描いた「影」すなわち$\zcol{\vec a}$に垂直な面への射影が関係してくる。垂直な成分を${}_\bot$をつけて表すと、$\vec b_\bot,\vec c_\bot$と$(\vec b+\vec c)_{\bot}$は次の図(上の図を$\zcol{\vec a}$の向かう方向から見下ろしたところと思えばよい)のような関係にある。
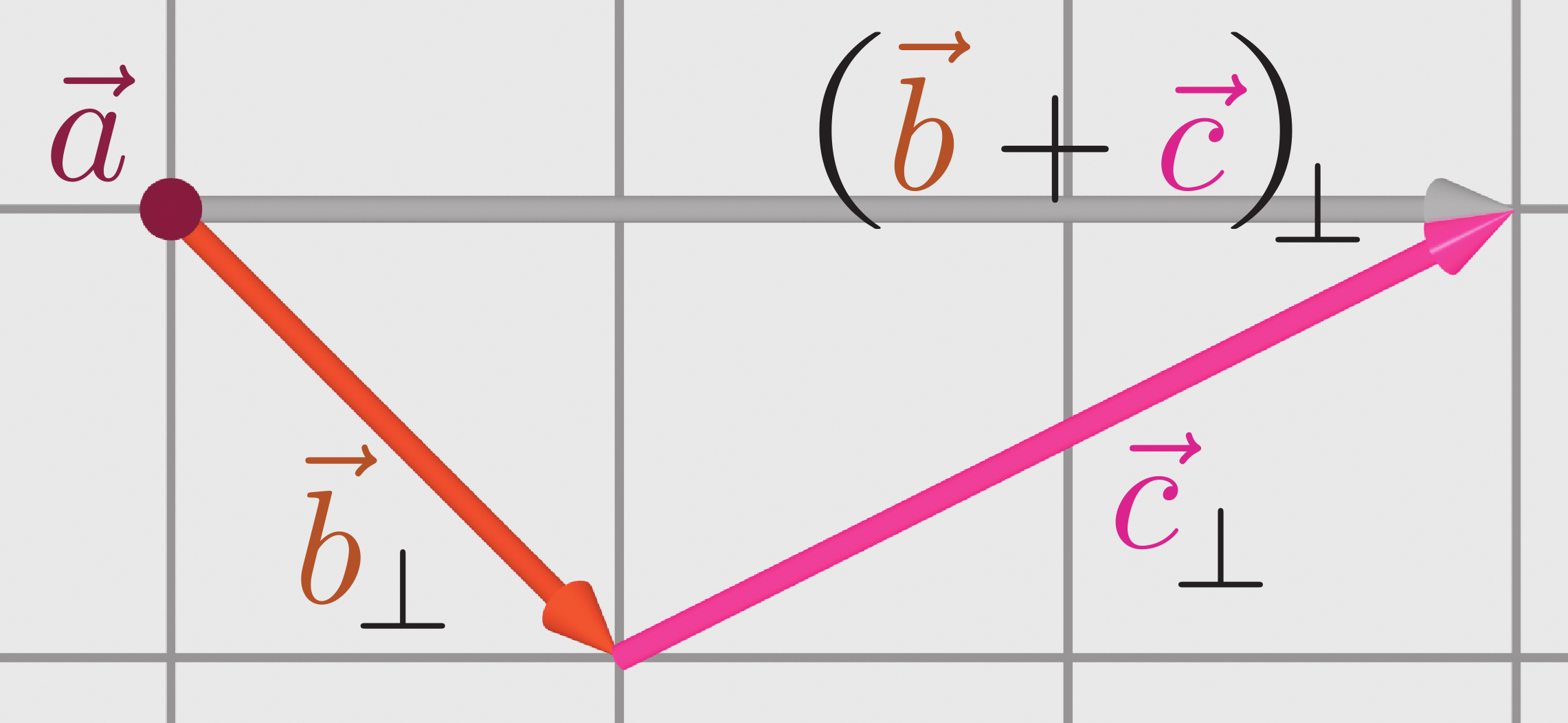
よって、$(\xcol{\vec b}+\ycol{\vec c})_\bot$は$\xcol{\vec b}_\bot+\ycol{\vec c}_\bot$とも書けることに注意しよう。すなわち「足算する」と「射影する」の順番はどちらが先でも結果は同じである。
$\zcol{\vec a}$と平行な成分は外積を取る時点で消えてしまうので、分配法則の成立を示すには、
\begin{equation}
\zcol{\vec a}\times(\xcol{\vec b}+\ycol{\vec c})_\bot=\zcol{\vec a}\times\xcol{\vec b}_\bot+\zcol{\vec a}\times \ycol{\vec c}_\bot\label{abcbot}
\end{equation}
を示せば十分である。
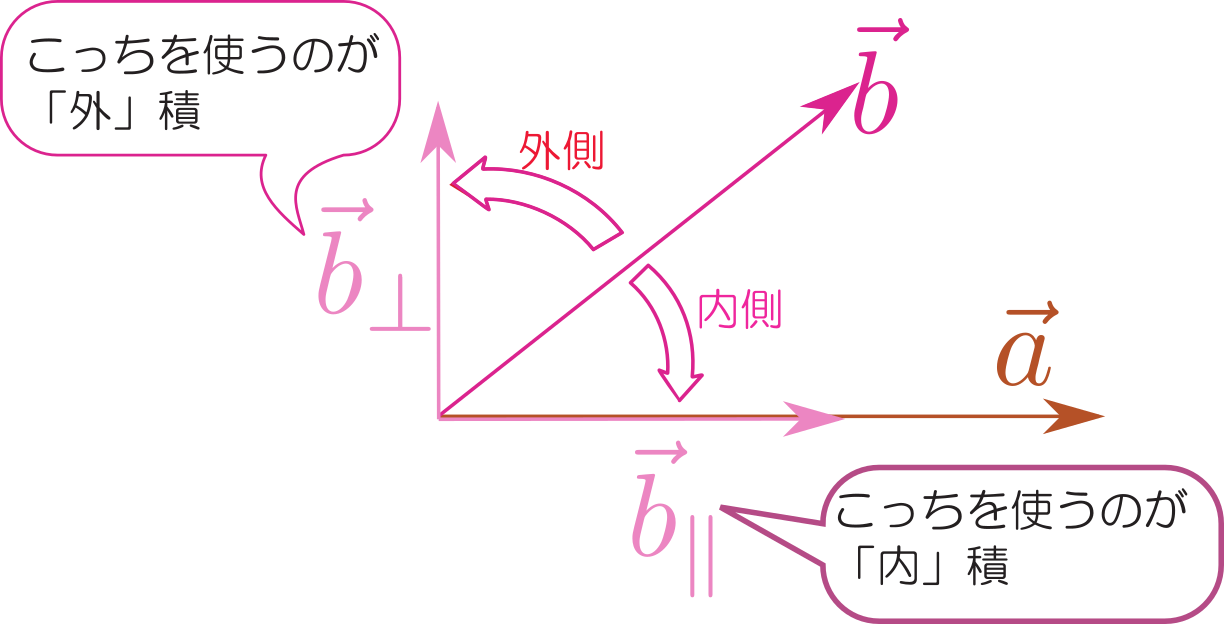
$|\zcol{\vec a}\times\xcol{\vec b}|=|\zcol{\vec a}||\xcol{\vec b}_\bot|$}のような式が成立するから、上の式に現れる三つのベクトルの大きさは、

のような三つの長方形の面積となる(足算が成立するのは面積ベクトルに対してであって、面積の大きさそのものに対しては成立しないことに注意)。
一番左の図に示した長方形の面積$|\zcol{\vec a}\times(\xcol{\vec b}+\ycol{\vec c})_\bot|$は、$|\zcol{\vec a}\times(\xcol{\vec b}+\ycol{\vec c})|$と書いても同じ値である。そしてそれぞれのベクトルの向きは面の法線の方向を向く。我々が示したいのは、(\ref{abcbot})が成立することである。つまり、外積の分配法則は三角柱の三つの側面の面積に関する法則にもなっているのである。
具体的な計算でも確認しておく。三角柱を真上から見た図で考えよう。

三つのベクトル$\xcol{\vec b}_\bot,\ycol{\vec c}_\bot, (\xcol{\vec b}+\ycol{\vec c})_\bot$が三角形を作っている。$\zcol{\vec a}\times\xcol{\vec b}_\bot,\zcol{\vec a}\times \ycol{\vec c}_\bot,\zcol{\vec a}\times(\xcol{\vec b}+\ycol{\vec c})_\bot$($\zcol{\vec a}\times\xcol{\vec b},\zcol{\vec a}\times \ycol{\vec c},\zcol{\vec a}\times(\xcol{\vec b}+\ycol{\vec c})$と書いても同じ)も三角形を作る。$\xcol{\vec b}_\bot$から$\zcol{\vec a}\times\xcol{\vec b}$をつくるという計算は「上から見て反時計回りに90度回して、$|\zcol{\vec a}|$を掛ける」という計算になる(図は$|\zcol{\vec a}|=1$の場合で描いた)。
$\zcol{\vec c}_\bot,(\ycol{\vec b}+\zcol{\vec c})_\bot$に関しても同様のことが言えるので、$\zcol{\vec a}\times\xcol{\vec b},\zcol{\vec a}\times \ycol{\vec c},\zcol{\vec a}\times(\xcol{\vec b}+\ycol{\vec c})$というベクトルはちゃんと図のとおりに三角形を作る。これで、分配法則が証明できた。
以上で第3回の授業は終わりです。
物理数学I webclass
この感想・コメントシートに書かれたことについては、代表的なものに対しては次のページで返答します。
なお、webClassに情報を載せていますが、授業があった日の午後7時より約1時間、オンラインオフィスアワーとしてzoomを開いてます。質問や相談などがある人は来て話してください。
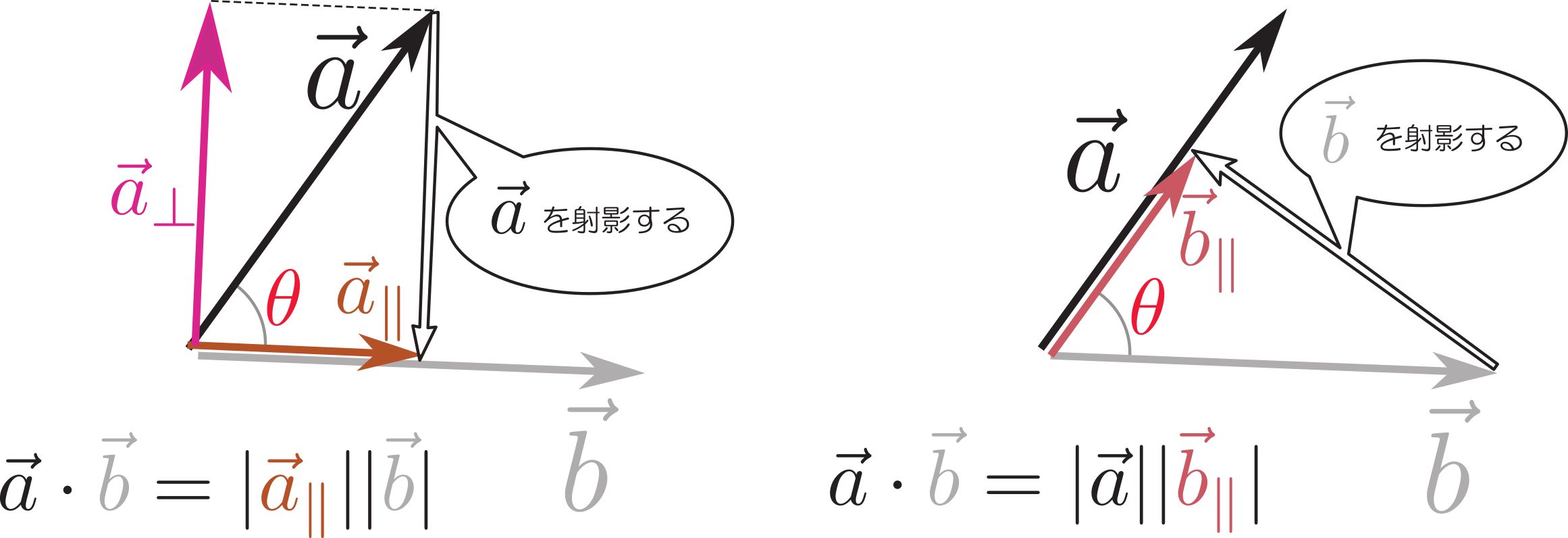



 を「サイクリック置換」と呼ぶ。
を「サイクリック置換」と呼ぶ。