「物理数学Ⅰ」2021年度講義録第4回

前回の感想・コメントシートから

　前回の授業の「感想・コメント」の欄に書かれたことと、それに対する返答は、

にありますので見ておいてください。

　では、前回の続きから。

外積の成分表示での計算法

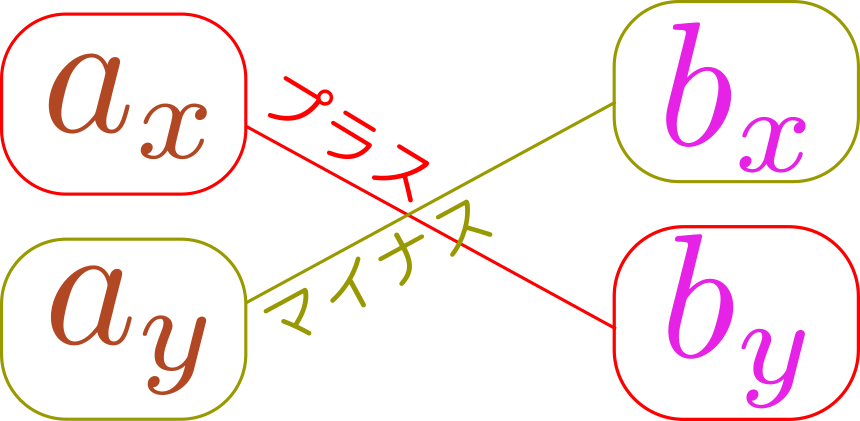
　分配法則が成立するおかげで、2次元ベクトルを$\xcol{\vec a}=\xcol{a_x}\ve_x+\xcol{a_y}\ve_y$と$\ycol{\vec b}=\ycol{b_x}\ve_x+\ycol{b_y}\ve_y$とすると、 \begin{equation} \begin{array}{rl} \xcol{\vec a}\times \ycol{\vec b} =&\left(\xcol{a_x}\ve_x+\xcol{a_y}\ve_y\right)\times\left(\ycol{b_x}\ve_x+\ycol{b_y}\ve_y\right)\\[2mm] &+\gunderbrace{\xcol{a_x}\ve_x\times \ycol{b_x}\ve_x}_{=0} +\xcol{a_x}\ve_x\times \ycol{b_y}\ve_y\\ &+\xcol{a_y}\ve_y \times \ycol{b_x}\ve_x +\gunderbrace{\xcol{a_y}\ve_y \times \ycol{b_y}\ve_y}_{=0}\\ =&\xcol{a_x}\ycol{b_y} \ve_x\times \ve_y +\xcol{a_y} \ycol{b_x} \ve_y \times \ve_x\\ =& \xcol{a_x}\ycol{b_y}-\xcol{a_y}\ycol{b_x} \end{array} \end{equation} のように外積が計算できる。2次元の外積という計算は、ベクトルの成分で言うと「$x$成分と$y$成分の積を、符号を変えて足す」という量になる。「外積には、同じ方向の成分は効かない」ということを思い出すと、$\xcol{a_x}\ycol{b_x}$のような項が出てこないことに納得が行くだろう。

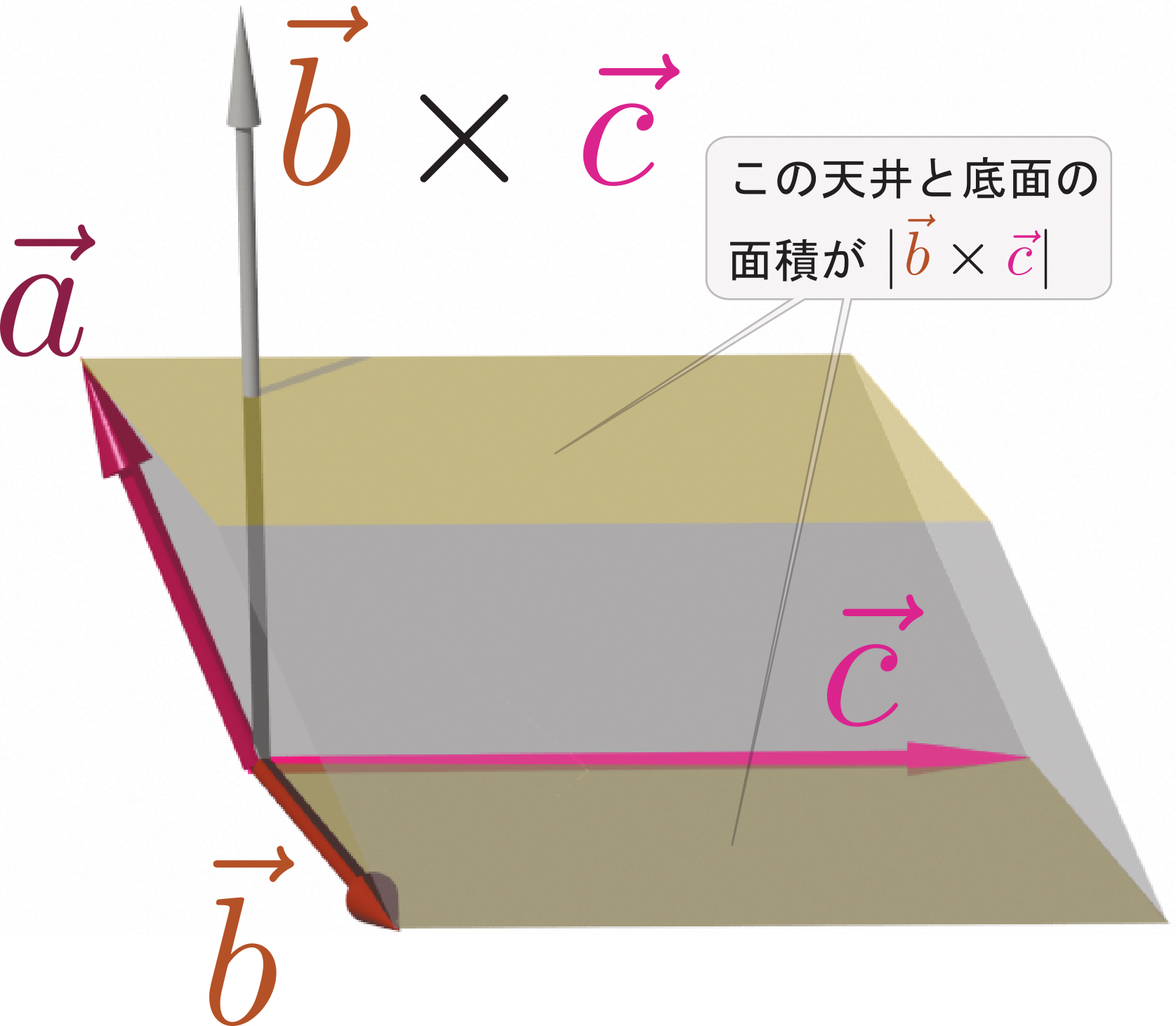
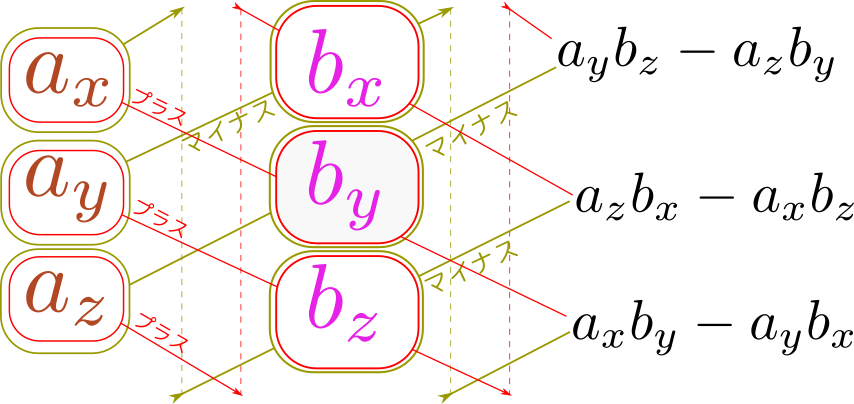
　二つの3次元ベクトル$\xcol{\vec a}=\xcol{a_x}\ve_x+\xcol{a_y}\ve_y+\xcol{a_z}\ve_z$と$\ycol{\vec b}=\ycol{b_x}\ve_x+\ycol{b_y}\ve_y+\ycol{b_z}\ve_z$の外積を計算する。まず \begin{align} \xcol{\vec a}\times \ycol{\vec b}=& \left(\xcol{a_x}\ve_x+\xcol{a_y}\ve_y+\xcol{a_z}\ve_z\right)\times \left(\ycol{b_x}\ve_x+\ycol{b_y}\ve_y+\ycol{b_z}\ve_z\right) \\ =& \kesi{\xcol{a_x}\ve_x\times \ycol{b_x}\ve_x} +\xcol{a_x}\ve_x\times \ycol{b_y}\ve_y +\xcol{a_x}\ve_x\times \ycol{b_z}\ve_z\\ +&\xcol{a_y}\ve_y\times \ycol{b_x}\ve_x +\kesi{\xcol{a_y}\ve_y\times \ycol{b_y}\ve_y} +\xcol{a_y}\ve_y\times \ycol{b_z}\ve_z\\ +&\xcol{a_z}\ve_z\times \ycol{b_x}\ve_x +\xcol{a_z}\ve_z\times \ycol{b_y}\ve_y +\kesi{\xcol{a_z}\ve_z\times \ycol{b_z}\ve_z} \end{align} となる。同じ方向を向いたベクトルどうしの外積は0となることを使って消せる。 \begin{equation} \begin{array}{ll} \\ \ve_x\times\ve_y=\ve_z,~~~ & \ve_y\times\ve_x=-\ve_z,\\ \ve_y\times\ve_z=\ve_x,~~~ & \ve_z\times\ve_y=-\ve_x,\\ \ve_z\times\ve_x=\ve_y,~~~ & \ve_x\times\ve_z=-\ve_y \end{array} \end{equation} という関係式を使って、 \begin{equation} \begin{array}{rl} & \xcol{a_x}\ycol{b_y}\gunderbrace{ \ve_x\times \ve_y}_{\ve_z} +\xcol{a_x}\ycol{b_z}\gunderbrace{\ve_x\times \ve_z}_{-\ve_y} +\xcol{a_y}\ycol{b_x}\gunderbrace{\ve_y\times \ve_x}_{-\ve_z} \\ +&\xcol{a_y}\ycol{b_z}\gunderbrace{\ve_y\times \ve_z}_{\ve_x} +\xcol{a_z}\ycol{b_x}\gunderbrace{\ve_z\times \ve_x}_{\ve_y} +\xcol{a_z}\ycol{b_y}\gunderbrace{\ve_z\times \ve_y}_{-\ve_x} \end{array}\end{equation} となり、

というのが答えである。

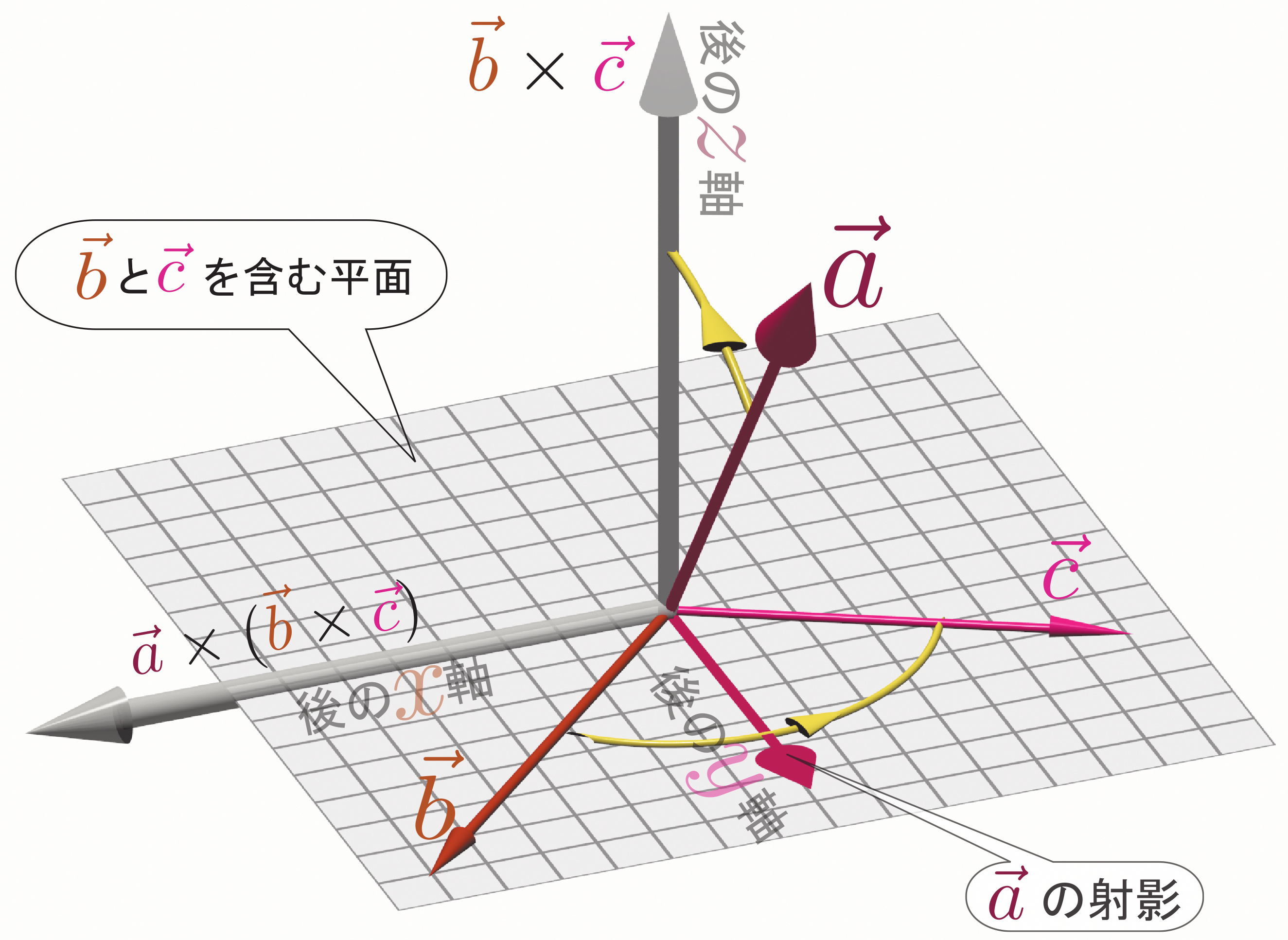
　このような$\xcol{\vec a},\ycol{\vec b}$の成分それぞれについて1次の式の形で書けるということから、「線形結合を作ってから外積を取ることと、外積を取ってから線形結合を作ることは同じ（$(\alpha\xcol{\vec a}+\beta\ycol{\vec b})\times\zcol{\vec c}=\alpha\xcol{\vec a}\times \zcol{\vec c}+\beta\ycol{\vec b}\times\zcol{\vec c}$および$(\zcol{\vec c}\times\alpha\xcol{\vec a}+\beta\ycol{\vec b})=\alpha\zcol{\vec c}\times\xcol{\vec a}+\beta\zcol{\vec c}\times\ycol{\vec b}$）」という性質がある。

　よって、外積（実は内積も）は双線形である。

　3次元の外積の成分の式$\xcol{\vec a}\times \ycol{\vec b}=\left(\xcol{a_y}\ycol{b_z}-\xcol{a_z}\ycol{b_y}\right)\ve_x+\left(\xcol{a_z}\ycol{b_x}-\xcol{a_x}\ycol{b_z}\right)\ve_y+\left(\xcol{a_x}\ycol{b_y}-\xcol{a_y}\ycol{b_x}\right)\ve_z$は、たくさんの項があってごちゃごちゃして見えるかもしれないが、この項は一定のルールで作られている。

　図に示すなら以下のような感じだ。

　数式の方の規則性も見ておこう。すべての項は$\xcol{a_{い}}\ycol{b_{ろ}}\ve_{は}$という式になっているが、その下付き添字（${}_い,{}_ろ,{}_は$）には$x,y,z$が1個ずつ入っていて、「い→ろ→は」が、という順番（$x,y,z$の偶置換）のときはそのまま、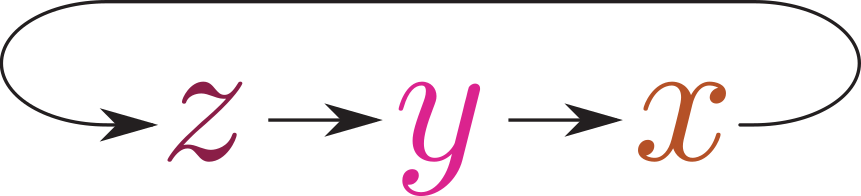という順番（$x,y,z$の奇置換）のときはマイナス符号をつけて、足すという計算をしている。

　「という順番」とは、$x,y,z$のどれから始めてもいいが、矢印の順番に三つを踏破する、という意味である（全部書いてしまうと、$\xcol{x}\to \ycol{y}\to \zcol{z}$と$\ycol{y}\to \zcol{z} \to \xcol{x}$と$\zcol{z}\to \xcol{x} \to \ycol{y}$である）。

　あるいは

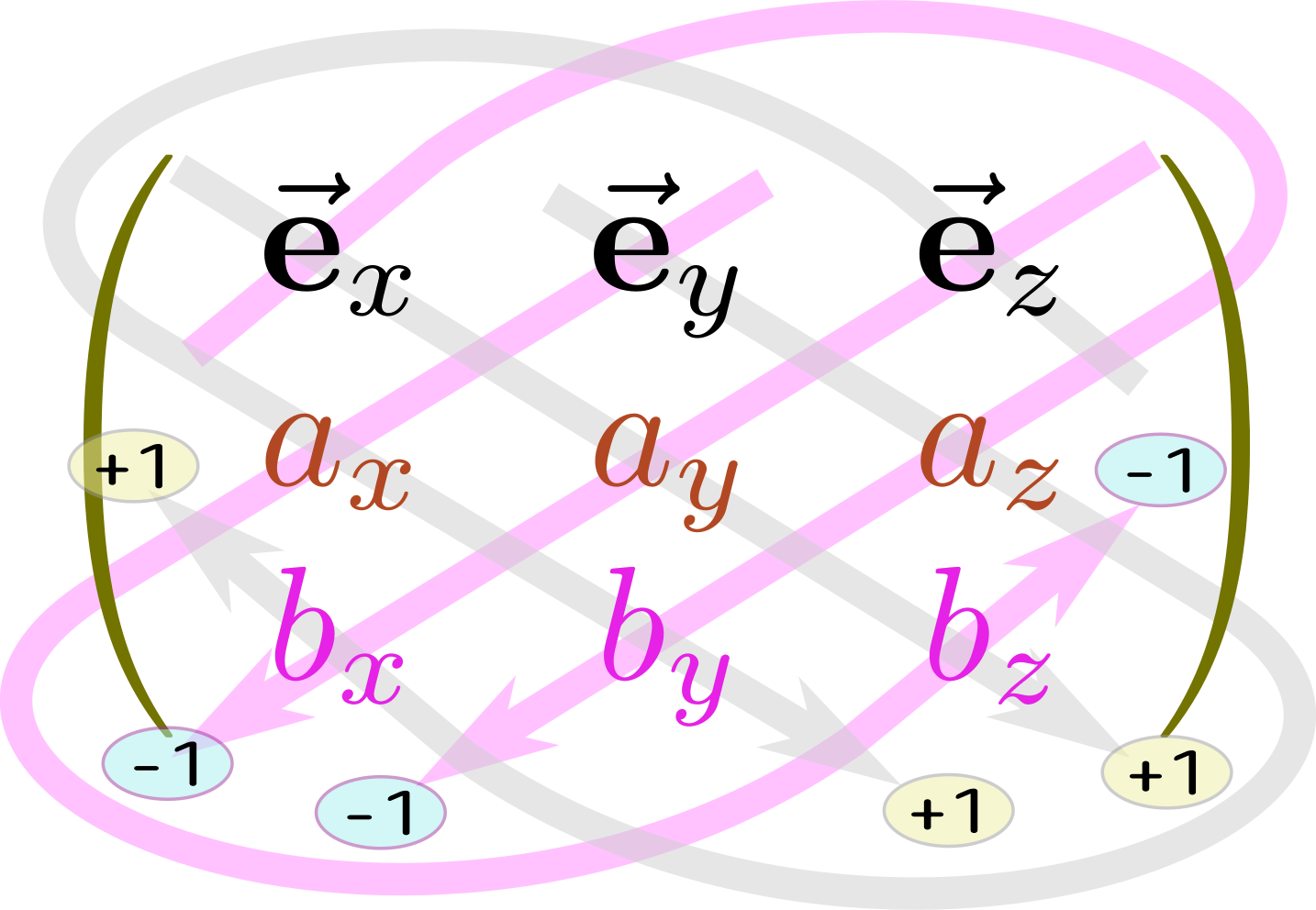
のように基底ベクトルとベクトルの成分を並べて、「各行から一つずつ選んで掛け算する」「偶置換の順番のときは$+1$、奇置換の順番のときは$-1$を掛ける」というルールにしたがって可能なすべての組合せを足していく、という操作を行った結果が外積である、と考えてもよい。

レヴィ・チビタ記号

レヴィ・チビタ記号

レヴィ・チビタ記号

　外積（そしてこれから先に出てくる行列式）を表現するために便利な記号として、「レヴィ・チビタ記号（Levi-Civita symbol）」を以下のように定義する（ただし以下の定義は3次元の場合である。

　この定義からわかるように、$\epsilon_{ijk}$は、添字$i,j,k$の中に同じものがあると0になる（例：$\epsilon_{113}=0$）。また、

を持つ（両辺が偶置換でたどりつけることはすぐに確認できる）。隣り合う添字を取り替えると符号が逆になる（$\epsilon_{ijk}=-\epsilon_{jik},\epsilon_{ijk}=-\epsilon_{ikj}$）のは定義から明らかであるが、隣り合っていない添字（$\epsilon_{ijk}$の$i$と$k$）も同様である。それは \begin{equation} \epsilon_{ijk}=-\epsilon_{jik}=\epsilon_{jki}=-\epsilon_{kji} \end{equation} のようにして確認できる。つまり、レヴィ・チビタ記号はどの添字の交換に対しても反対称である（交換しても同じであるとき「対称」、交換すると符号が変わる（絶対値は同じ）とき「反対称」と言う）。

この記号を使って書くと、 \begin{equation} (\xcol{\vec a}\times\ycol{\vec b})_i = \sum_{\dum[rcolor]{j},\dum[thetacolor]{k}}\epsilon_{i\,\dml[rcolor]{j}\dml[thetacolor]{k}}\xcol{a_{\dmr[rcolor]{{j}}}}\ycol{b_{\dmr[thetacolor]{{k}}}} \end{equation} と書くことができる。実際$i=1$の場合を計算してみると \begin{equation} (\xcol{\vec a}\times\ycol{\vec b})_1 = \epsilon_{123}\xcol{a}_{2}\ycol{b}_{3} +\epsilon_{132}\xcol{a}_{3}\ycol{b}_{2}=\xcol{a}_{2}\ycol{b}_{3}-\xcol{a}_{3}\ycol{b}_{2} \end{equation} となる(2,3も同様)。

　この記号を使って外積を表現すると \begin{align} \xcol{\vec a}\times\ycol{\vec b}= \sum_{\dum[xcolor]{i},\dum[ycolor]{j},\dum[zcolor]{k}=1}^3\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}}\ve_{\dmr[xcolor]{i}}a_{\dmr[ycolor]{j}} b_{\dmr[zcolor]{k}} \end{align} になる。$\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}\dml[zcolor]{k}}$を掛けて足すという操作が、前ページに描いた図の操作と同じことなのである。

　順序は逆になったが、2次元の外積も

を使って、2次元の外積を \begin{align} \xcol{\vec a}\times\ycol{\vec b}= \sum_{\dum[xcolor]{i},\dum[ycolor]{j}=1}^2\epsilon_{\dml[xcolor]{i}\dml[ycolor]{j}}a_{\dmr[xcolor]{i}} b_{\dmr[ycolor]{j}} \end{align} と書くことができる。ちょっと先走って行列の書き方を使っておくと、 \begin{align} \xcol{\vec a}\times\ycol{\vec b}= \mtx{\xcol{a_x}&\xcol{a_y}}\mtx{0&1\\-1&0}\mtx[c]{\ycol{b_x}\\\ycol{b_y}} \end{align} となる（2次元のレヴィ・チビタ記号は行列で表すこともできる）。

　こうなると4次元以上はどうなるの？---と聞きたくなるところだが、それはずっと後で考えよう。

前回の感想・コメントシートから スカラー3重積

スカラー3重積

　ベクトルの内積・外積に関するいくつかの公式を示す。

という式を考えよう。

　内積は交換するので、この式は$(\ycol{\vec b}\times \zcol{\vec c})\cdot\xcol{\vec a}= (\zcol{\vec c}\times \xcol{\vec a})\cdot\ycol{\vec b} =(\xcol{\vec a}\times \ycol{\vec b})\cdot\zcol{\vec c}$と書いても同じことである。ベクトル三つをつかって結果がスカラーなのでこの名前で呼ぶ。

　この式には

のような幾何学的意味がある。三つのベクトル$\zcol{\vec a},\xcol{\vec b},\ycol{\vec c}$の根本を揃えた平行六面体を考えると、$\ycol{\vec b}\times\zcol{\vec c}$は$\ycol{\vec b}$と$\zcol{\vec c}$が作る平行四辺形の面積の大きさを持ち、その法線の方向を向いたベクトルである。それと$\xcol{\vec a}$の内積を取った結果$\xcol{\vec a}\cdot(\ycol{\vec b}\times\zcol{\vec c})$は、$|\ycol{\vec b}\times\zcol{\vec c}|$という底面積に、$|\xcol{\vec a}|\cos\theta$（$\theta$は$\xcol{\vec a}$と$\ycol{\vec b}\times\zcol{\vec c}$の角度）という高さを掛けたものであるから、この三つのベクトルで作った平行六面体の体積である。どれを底面に選んでも面積は同様に計算できるから、残り二つと等しいこともわかる。

$\xcol{\vec a}\cdot(\ycol{\vec b}\times \zcol{\vec c}) = \ycol{\vec b}\cdot(\zcol{\vec c}\times \xcol{\vec a}) = \zcol{\vec c}\cdot(\xcol{\vec a}\times \ycol{\vec b})$が平行六面体の体積であることを反映して、$\xcol{\vec a},\ycol{\vec b},\zcol{\vec c}$が線形従属である場合、この値は0になる。このことを計算で確認せよ。答えがわかったら開くこと。

　線形従属だということは、$\vec c=\alpha\vec b+\beta \vec c$となるような$\alpha,\beta$が見つけられるということ。

　$\vec c=\alpha\vec a+\beta \vec b$を代入すると、 \begin{align} \xcol{\vec a}\cdot(\ycol{\vec b}\times\goverbrace{(\alpha\vec a+\gunderbrace{\beta \vec b}_{外積で0})}^{\vec c}) = \alpha \xcol{\vec a}\cdot\gunderbrace{(\ycol{\vec b}\times \vec a)}_{\xcol{\vec a}と垂直}=0 \end{align} となる。$\ycol{\vec b}\cdot(\zcol{\vec c}\times \xcol{\vec a})$も同様。 \begin{align} \goverbrace{(\alpha\vec a+\beta \vec b)}^{\zcol{\vec c}}\cdot\gunderbrace{(\xcol{\vec a}\times \ycol{\vec b})}_{\vec aとも\vec bとも垂直}=0 \end{align}

video

　上の三つの式をレヴィ・チビタの記号を使う書き方で表現する方法の説明を、ビデオと文章で示す。

\begin{align} \xcol{\vec a}\cdot(\ycol{\vec b}\times\zcol{\vec c})=& \sum_{\dum[rcolor]{i},\dum[thetacolor]{j},\dum[phicolor]{k}}\xcol{a_{\dml[rcolor]{{i}}}} \epsilon_{\dmr[rcolor]{i}\dml[thetacolor]{j}\dml[phicolor]{k}}\ycol{b_{\dmr[thetacolor]{{j}}}} \zcol{c_{\dmr[phicolor]{{k}}}}\\[5mm] \ycol{\vec b}\cdot(\zcol{\vec c}\times\xcol{\vec a})=& \sum_{\dum[rcolor]{i},\dum[thetacolor]{j},\dum[phicolor]{k}}\ycol{b_{\dml[rcolor]{{i}}}} \epsilon_{\dmr[rcolor]{i}\dml[thetacolor]{j}\dml[phicolor]{k}}\zcol{c_{\dmr[thetacolor]{{j}}}} \xcol{a_{\dmr[phicolor]{{k}}}}\\[5mm] \zcol{\vec c}\cdot(\xcol{\vec a}\times\ycol{\vec b})=& \sum_{\dum[rcolor]{i},\dum[thetacolor]{j},\dum[phicolor]{k}}\zcol{c_{\dml[rcolor]{{i}}}} \epsilon_{\dmr[rcolor]{i}\dml[thetacolor]{j}\dml[phicolor]{k}}\xcol{a_{\dmr[thetacolor]{{j}}}} \ycol{b_{\dmr[phicolor]{{k}}}} \end{align} となる。

　$\sum$の足し上げに使っている添字$\dum[rcolor]{i},\dum[thetacolor]{j},\dum[phicolor]{k}$はダミー添字なので、添字を変えてもよい。つまり、$\sum_{\dum[rcolor]{i}}（なんとか）\!_{\dum[rcolor]{i}}$と書いても、$\sum_{\dum[thetacolor]{j}} （なんとか）\!_{\dum[thetacolor]{j}}$と書いても、内容は変わらない。これを使って上の2個目と3個目の式の$\dum[rcolor]{i},\dum[thetacolor]{j},\dum[phicolor]{k}$を書き換えると、 \begin{align} \xcol{\vec a}\cdot(\ycol{\vec b}\times\zcol{\vec c})=& \sum_{\dum[rcolor]{i},\dum[thetacolor]{j},\dum[phicolor]{k}}\xcol{a_{\dml[rcolor]{{i}}}} \epsilon_{\dmr[rcolor]{i}\,\dml[thetacolor]{j}\dml[phicolor]{k}}\ycol{b_{\dmr[thetacolor]{{j}}}} \zcol{c_{\dmr[phicolor]{{k}}}}\\[5mm] \ycol{\vec b}\cdot(\zcol{\vec c}\times\xcol{\vec a})=&\goverbrace{ \sum_{\dum[rcolor]{i},\dum[thetacolor]{j},\dum[phicolor]{k}}\ycol{b_{\dml[thetacolor]{{j}}}} \epsilon_{\dmr[thetacolor]{j}\,\dml[phicolor]{k}\dml[rcolor]{i}}\zcol{c_{\dmr[phicolor]{{k}}}} \xcol{a_{\dmr[rcolor]{{i}}}}}^{\dum[rcolor]{i}\to\dum[thetacolor]{j},\dum[thetacolor]{j}\to \dum[phicolor]{k},\dum[phicolor]{k}\to\dum[rcolor]{i}と置換}\\[5mm] \zcol{\vec c}\cdot(\xcol{\vec a}\times\ycol{\vec b})=&\goverbrace{ \sum_{\dum[rcolor]{i},\dum[thetacolor]{j},\dum[phicolor]{k}}\zcol{c_{\dml[phicolor]{\zcol{k}}}} \epsilon_{\dmr[phicolor]{k}\,\dml[rcolor]{i}\dml[thetacolor]{j}}\xcol{a_{\dmr[rcolor]{{i}}}} \ycol{b_{\dmr[thetacolor]{{j}}}}}^{\dum[rcolor]{i}\to\dum[phicolor]{k},\dum[thetacolor]{j}\to \dum[rcolor]{i},\dum[phicolor]{k}\to\dum[thetacolor]{j}と置換} \label{epsilonijkjki} \end{align} のように、$\xcol{a},\ycol{b},\zcol{c}$に付いた添字を共通化して和記号の中身を$\begin{cases} \epsilon_{\dml[rcolor]{i}\dml[thetacolor]{j}\dml[phicolor]{k}}\xcol{a_{\dmr[rcolor]{{i}}}} \ycol{b_{\dmr[thetacolor]{{j}}}}\zcol{c_{\dmr[phicolor]{{k}}}} \\ \epsilon_{\dml[thetacolor]{j}\dml[phicolor]{k}\dml[rcolor]{i}}\xcol{a_{\dmr[rcolor]{{i}}}} \ycol{b_{\dmr[thetacolor]{{j}}}}\zcol{c_{\dmr[phicolor]{{k}}}} \\ \epsilon_{\dml[phicolor]{k}\dml[rcolor]{i}\dml[thetacolor]{j}}\xcol{a_{\dmr[rcolor]{{i}}}} \ycol{b_{\dmr[thetacolor]{{j}}}}\zcol{c_{\dmr[phicolor]{{k}}}} \end{cases}$とすることができる。

　レヴィ・チビタ記号は \begin{equation} \epsilon_{ijk}=\epsilon_{jki}=\epsilon_{kij} \end{equation} を満たすから、これでスカラー3重積の式が示せたことになる。

レヴィ・チビタ記号 ベクトル3重積

ベクトル3重積

　次に、外積を二回行う計算である

を示そう。

　上の式を、まず立体的に図を描いて考えてみよう。

以下の計算の説明ビデオが↓

　計算過程で現れる$\xcol{\vec b}\times\ycol{\vec c}$は$\xcol{\vec b}$と$\ycol{\vec c}$を含む平面の法線ベクトル（$\xcol{\vec b}\to \ycol{\vec c}$と右ネジを回すときにネジが進む向き）である。計算結果である$\zcol{\vec a}\times(\xcol{\vec b}\times\ycol{\vec c})$は$\zcol{\vec a}\to(\xcol{\vec b}\times\ycol{\vec c})$と右ネジを回すときにネジが進む方向を向く。その結果は$\xcol{\vec b}\times\ycol{\vec c}$と垂直になるはずだから、答えのベクトルはこの平面の上にある。

ここで「$\xcol{\vec b}$と$\ycol{\vec c}$が平行だったらどうしよう？」という点に気づいた人もいるかもしれない。その場合、$\xcol{\vec b}\times\ycol{\vec c}=0$だから、この後の計算は全く意味がない。しかしその時、右辺の$(\zcol{\vec a}\cdot\ycol{\vec c})\xcol{\vec b} - (\zcol{\vec a}\cdot\xcol{\vec b})\ycol{\vec c}$も0である（そのことは$\ycol{\vec c}=k\xcol{\vec b}$と代入すればすぐに確認できる）。だからその場合でも公式は成り立つので心配はない。

　よってこの答は、後で求める定数$\beta,\gamma$を使って \begin{equation} \zcol{\vec a}\times(\xcol{\vec b}\times\ycol{\vec c})= \beta\xcol{\vec b} + \gamma\ycol{\vec c} \end{equation} という形で書ける。$\zcol{\vec a}\times(\xcol{\vec b}\times \ycol{\vec c})$は$\zcol{\vec a}$とも垂直であることを使うと、 \begin{equation} \beta\zcol{\vec a}\cdot \xcol{\vec b} + \gamma\zcol{\vec a}\cdot \ycol{\vec c}=0 \end{equation} であるから、$\beta:\gamma=(\zcol{\vec a}\cdot \ycol{\vec c}):-(\zcol{\vec a}\cdot \xcol{\vec b})$である。そこで$\beta=\alpha(\zcol{\vec a}\cdot\ycol{\vec c}),\gamma=-\alpha(\zcol{\vec a}\cdot\xcol{\vec b})$と置くことにして、 \begin{equation} \zcol{\vec a}\times(\xcol{\vec b}\times\ycol{\vec c})= \alpha \left( ( \zcol{\vec a}\cdot\ycol{\vec c}) \xcol{\vec b} -(\zcol{\vec a}\cdot \xcol{\vec b}) \ycol{\vec c} \right) \end{equation} までわかった。

　ここまでは図形で考えたから、どういう座標系で考えるかによらず、正しい式であるが、最後に残った未知数$\alpha$を求めるために、ここで座標系を設定することにしよう。ベクトル$\zcol{\vec a}$の方向に$\zcol{z}$軸をとって、$\zcol{\vec a}=(0,0,\zcol{a_z})$とする。すると左辺の$\xcol{x}$成分は \begin{align} -\zcol{a_z}(\xcol{\vec b}\times\ycol{\vec c})_y= -\zcol{a_z}(\xcol{b_z}\ycol{c_x}+\xcol{b_x}\ycol{c_z}) \end{align} となる。一方右辺の$\xcol{x}$成分は（$\zcol{\vec a}\cdot\ycol{\vec c}=\zcol{a_z}\ycol{c_z},\zcol{\vec a}\cdot \xcol{\vec b}=\zcol{a_z}\xcol{b_z}$なので） \begin{align} \alpha \left(\zcol{a_z}\ycol{c_z}\xcol{b_x}-\zcol{a_z}\xcol{b_z}\ycol{c_x}\right) \end{align} である。見比べると$\alpha=1$がわかる（$\ycol{y}$成分、$\zcol{z}$成分についてもこの式が正しいことはすぐに確認できる）。

以下にレヴィ・チビタ記号を使った計算の説明を示す。ビデオは↓

　レヴィ・チビタ記号を使った計算でも、この式を示すことができる。$\zcol{\vec a}\times(\xcol{\vec b}\times\ycol{\vec c})$の$i$成分は \begin{equation} \sum_{\dum[xcolor]{j},\dum[ycolor]{k}} \epsilon_{i\dml[xcolor]{j}\dml[ycolor]{k}} \zcol{a_{\dmr[xcolor]{j}}} \goverbrace{\sum_{\dum{m}\dum{n}}\epsilon_{\dmr[ycolor]{k}\,\dml[zcolor]{m}\dml{n}}\xcol{b_{\dmr[zcolor]{m}}}\ycol{c_{\dmr{n}}}}^{\xcol{\vec b}\times\ycol{\vec c}のk成分} \end{equation} と表すことができる。ここで \begin{equation} \sum_{\dum[ycolor]{k}} \epsilon_{ij\dml[ycolor]{k}} \epsilon_{\dmr[ycolor]{k}mn}=\delta_{im}\delta_{jn}-\delta_{in}\delta_{jm}\label{epep} \end{equation} を示すことができる。

証明はここを開くと出てくる。

　まず以下の式(A) \begin{align} \epsilon_{ijk}\epsilon_{\ell mn} = \delta_{i\ell}\delta_{jm}\delta_{kn} +\delta_{im}\delta_{jn}\delta_{k\ell} +\delta_{in}\delta_{j\ell}\delta_{km} -\delta_{i\ell}\delta_{jn}\delta_{km} -\delta_{im}\delta_{j\ell}\delta_{kn} -\delta_{in}\delta_{jm}\delta_{k\ell}\label{epseps}~~~~~{({\rm A})} \end{align} を示し、$k$と$\ell$を等しくして足し上げると上の式が出てくることを示そう。

　$i,j,k$が$1,2,3$の置換であり、$\ell,m,n$も$1,2,3$の置換であるときにのみ、 $\epsilon_{ijk}\epsilon_{\ell mn}$は0ではない。$i,j,k$が$1,2,3$およびそのサイクリック置換なら$1$、$1,3,2$およびそのサイクリック置換なら$-1$と考えると、 \begin{align} \epsilon_{ijk}\gunderbrace{\epsilon_{1 23}}_1 = \delta_{i1}\delta_{j2}\delta_{k3} +\delta_{i2}\delta_{j3}\delta_{k1} +\delta_{i3}\delta_{j1}\delta_{k2} -\delta_{i1}\delta_{j3}\delta_{k2} -\delta_{i2}\delta_{j1}\delta_{k3} -\delta_{i3}\delta_{j2}\delta_{k1}\label{eonetwothree} \end{align} という式を作ることができる（これで$i,j,k$のうちどれか二つが等しいときには0という性質も持っている）。

この式を、求めたい式(A)に$\ell=1,m=2,n=3$を代入したものだと解釈する。元の式をもう一度見ると \begin{align} \epsilon_{ijk}\epsilon_{\ell mn} = \delta_{i\ell}\delta_{jm}\delta_{kn} +\delta_{im}\delta_{jn}\delta_{k\ell} +\delta_{in}\delta_{j\ell}\delta_{km} -\delta_{i\ell}\delta_{jn}\delta_{km} -\delta_{im}\delta_{j\ell}\delta_{kn} -\delta_{in}\delta_{jm}\delta_{k\ell} \end{align} であるが、この式はちゃんと$\ell,m,n$に関する反対称も持っていて、$\ell m n$が$123$の偶置換なら(A)と同じ式になり、$123$の奇置換なら(A)と符号が反対の式になる（$\ell,m,n$の中に等しいものがあれば0になるということも満たしている）。

　後はこの式で$\ell=k$として$k$を足し上げる。 \begin{align} \sum_{k=1}^3 \epsilon_{ijk}\epsilon_{k mn} = \sum_{k=1}^3\left( \delta_{ik}\delta_{jm}\delta_{kn} +\delta_{im}\delta_{jn}\delta_{kk} +\delta_{in}\delta_{jk}\delta_{km} -\delta_{ik}\delta_{jn}\delta_{km} -\delta_{im}\delta_{jk}\delta_{kn} -\delta_{in}\delta_{jm}\delta_{kk} \right) \end{align} となるが、足し算されることにより$\delta_{kk}\to 3$と置き換えられることを使うと、 \begin{align} \sum_{k=1}^3 \epsilon_{ijk}\epsilon_{k mn} =& \delta_{in}\delta_{jm} +3\delta_{im}\delta_{jn} +\delta_{in}\delta_{jm} -\delta_{im}\delta_{jn} -\delta_{im}\delta_{jn} -3\delta_{in}\delta_{jm}\nonumber\\ =&\delta_{im}\delta_{jn}-\delta_{in}\delta_{jm} \end{align} が導かれる。

　こうして$\zcol{\vec a}\times(\xcol{\vec b}\times\ycol{\vec c})$の$i$成分は \begin{equation} \begin{array}{rl} \sum_{\dum[rcolor]{j},\dum[thetacolor]{m},\dum[phicolor]{n}}\zcol{a_{\dml[rcolor]{j}}}\xcol{b_{\dml[thetacolor]{{m}}}} \ycol{c_{\dml[phicolor]{{n}}}} \left(\delta_{i\dmr[thetacolor]{m}}\delta_{\dmr[rcolor]{j}\dmr[phicolor]{n}}-\delta_{i\dmr[phicolor]{n}}\delta_{\dmr[rcolor]{j}\dmr[thetacolor]{m}}\right) =& \sum_{\dum[rcolor]{j}}\left( \zcol{a_{\dml[rcolor]{{j}}}}\xcol{b_{\kuro{i}}} \ycol{c_{\dmr[rcolor]{j}}}- \zcol{a_{\dml[rcolor]{{j}}}} \xcol{b_{\dmr[rcolor]{{j}}}} \ycol{c_{\kuro{i}}} \right) \end{array} \end{equation} となる。これは$(\zcol{\vec a}\cdot\ycol{\vec c})\xcol{\vec b}-(\zcol{\vec a}\cdot\xcol{\vec b})\ycol{\vec c}$の$i$成分である。

　$(\zcol{\vec a}\cdot\ycol{\vec c})\xcol{\vec b}$では、$\zcol{\vec a}$と$\ycol{\vec c}$は内積だから「$\zcol{a}$と$\ycol{b}$のダミーの添字は足しあげられている」と表現する。一方、$-(\zcol{\vec a}\cdot\xcol{\vec b})\ycol{\vec c}$の方では「$\zcol{a}$と$\xcol{b}$のダミーの添字は足し上げられている」となる。ダミーの添字が足し上げられていることをよく（「添字」を「脚」と表現して）「脚が潰れている」と表現する。逆に$(\zcol{\vec a}\cdot\ycol{\vec c})\xcol{\vec b}$では、「$\xcol{b}$の脚は潰れていない」し、$-(\zcol{\vec a}\cdot\xcol{\vec b})\ycol{\vec c}$では「$\ycol{c}$の脚は潰れていない」と言う。

スカラー3重積 その他の内積・外積に関する式

その他の内積・外積に関する式

　次に外積と外積の内積に関する式 \begin{equation} (\xcol{\vec a}\times \ycol{\vec b})\cdot(\zcol{\vec c}\times\thetacol{\vec d})= (\xcol{\vec a}\cdot\zcol{\vec c})(\ycol{\vec b}\cdot\thetacol{\vec d}) -(\xcol{\vec a}\cdot\thetacol{\vec d})(\ycol{\vec b}\cdot\zcol{\vec c})\label{gaisekidousi} \end{equation} を示そう。スカラー3重積の式を使って、 \begin{equation} (\xcol{\vec a}\times \ycol{\vec b})\cdot(\zcol{\vec c}\times \thetacol{\vec d}) =\zcol{\vec c}\cdot(\thetacol{\vec d}\times (\xcol{\vec a}\times \ycol{\vec b})) \end{equation} とする。$\thetacol{\vec d}\times (\xcol{\vec a}\times \ycol{\vec b})$にベクトル3重積の式を使えば、以下を得る。 \begin{equation} =\zcol{\vec c}\cdot( (\thetacol{\vec d}\cdot \ycol{\vec b})\xcol{\vec a}-(\thetacol{\vec d}\cdot\xcol{\vec a})\ycol{\vec b} ) =(\xcol{\vec a}\cdot \zcol{\vec c})(\ycol{\vec b}\cdot \thetacol{\vec d})-(\xcol{\vec a}\cdot \thetacol{\vec d})(\ycol{\vec b}\cdot \zcol{\vec c}) \end{equation}

　最後に

を示そう。同じ式を、$ (\xcol{\vec a}\times\ycol{\vec b})\times\zcol{\vec c}+(\ycol{\vec b}\times\zcol{\vec c})\times\xcol{\vec a}+(\zcol{\vec c}\times\xcol{\vec a})\times\ycol{\vec b}=0$と書いてもよい。

　証明は以下のようにして行なう。ベクトル3重積の式を使うと、この式の中に$\xcol{\vec a}$と同じ方向を向いた項が二つ、$\ycol{\vec b}\times(\zcol{\vec c}\times\xcol{\vec a})$から来る$-(\ycol{\vec b}\cdot\zcol{\vec c})\xcol{\vec a}$と$\zcol{\vec c}\times(\xcol{\vec a}\times\ycol{\vec b})$から来る$(\zcol{\vec c}\cdot\ycol{\vec b})\xcol{\vec a}$があり、これらが消し合うことがわかる。$\ycol{\vec b},\zcol{\vec c}$と同じ方向を向いた項についても同様である。

　$\zcol{\vec c}$が常に最後に来るように順番を変えることで、 \begin{align} \xcol{\vec a}\times(\ycol{\vec b}\times\zcol{\vec c}) -\ycol{\vec b}\times(\xcol{\vec a}\times\zcol{\vec c}) =(\xcol{\vec a}\times\ycol{\vec b})\times\zcol{\vec c}\label{jacobitwo} \end{align} と書き直せる。外積に限らず、「3つの項に2項演算を施す順番を変えて輪を取ると0になる」形の式が成り立つとき、それは「ヤコビ恒等式(Jacobi identity)」と呼ばれる。

　この式は、$\zcol{\vec c}$に対して$\boxed{\xcol{\vec a}\times}$という演算と$\boxed{\ycol{\vec b}\times}$という演算を左から施すときに、順番を替えたことによる差が$\boxed{(\xcol{\vec a}\times\ycol{\vec b})\times}$という演算になる、と言っている。この「演算子を掛ける順番を交換して差を取る」という操作をした結果を表す演算を「交換関係(commutation relation)または交換子(commutator)」と呼び、演算$\ope{A}$と演算$\ope{B}$の交換関係を \begin{align} \ope{A}(\ope{B}f)-\ope{B}(\ope{A}f)= \left[\ope{A},\ope{B}\right]f \end{align} と表現する（$f$は演算子の掛かる相手である）。交換関係の表記を使うと、ヤコビ恒等式を \begin{align} \left[\boxed{\xcol{\vec a}\times},\boxed{\ycol{\vec b}\times}\right]\zcol{\vec c} =\boxed{(\xcol{\vec a}\times\ycol{\vec b})\times}\zcol{\vec c} \end{align} と書くことができる。ヤコビ恒等式が成り立つことは、「二つの演算の交換関係が、別のパラメータを使った同種の演算になる」ということを示している。

ベクトル3重積 平面図形と内積・外積

平面図形と内積・外積

　以下ではベクトルを使って図形を表現する方法について考えていこう。

2次元の内積・外積と直線

　2次元平面上の直線を数式で表す方法として、

• (1)方程式$a\xcol{x}+b\ycol{y}=c$（←これを満たす点の集合が考えている直線）
• (2)媒介変数表示$\begin{cases}x\kakko{\tcol{t}}=k_x\tcol{t}+x_0\\y\kakko{\tcol{t}}=k_y\tcol{t}+y_0\end{cases}$（←$\tcol{t}$を変化させると直線上を動く）

がある。媒介変数表示では、$\tcol{t}$が独立変数で、$x,y$は$\tcol{t}$を決めると決まる、関数である（なので、$x\kakko{\tcol{t}}$のように書く）。一方(1)の方程式では、$\xcol{x},\ycol{y}$が変数。ただし、二つの変数の間に関係がついている。これらをベクトルを使って書き直すことを考えよう。

↑図は$\vec k=\mtx[c]{-2\\1},\vec k_\bot=\mtx[c]{1\\2}$の場合で描かれている。

　媒介変数表示の方は$x,y$成分が並んだ形をしているので、すぐにベクトルで書き直すことができて、 \begin{align} \gunderbrace{\mtx[c]{x\\y}}_{\vec x}=\gunderbrace{\mtx[c]{k_x\\ k_y}}_{\vec k}\tcol{t}+\gunderbrace{\mtx[c]{x_0\\y_0}}_{\vec x_0} \end{align} となる。短くこんなふうに短く書いてこそベクトルを使う甲斐があるというものだ。書けば$\vec x=\vec k\,\tcol{t}+\vec x_0$となる（物理でよく使う、等速直線運動のときの式$\vec x=\vec v\tcol{t}+\vec x_0$である）。

　ベクトル$\vec k=\mtx[c]{k_x\\k_y}$は直線の伸びていく方向を表すベクトルで、この直線の「方向ベクトル(direction vector)」と呼ばれる。

　媒介変数表示から媒介変数（パラメータ）$\tcol{t}$を「消す」と方程式$a\xcol{x}+b\ycol{y}=c$が得られるはずである。せっかくベクトル表記を作ったし、ベクトルの公式もたくさん求めておいたのだから、ベクトルの計算（内積・外積）を使ってやってみよう。「$\tcol{t}$を消す」ために、「$\vec k$と内積を取ったら消えるようなベクトルを見つけて内積を取る」という戦略を取る。すなわち、$\vec k_\bot\cdot \vec k=0$になるベクトル$\vec k_\bot$を見つけて、 \begin{align} \vec k_\bot\cdot \vec x=\gunderbrace{\vec k_\bot\cdot \vec k}_{=0}\,\tcol{t}+\vec k_\bot\cdot \vec x_0 \end{align} のような計算をするか、「$\vec k$と外積を取る」という計算 \begin{align} \vec x\times \vec k=\gunderbrace{\vec k\times \vec k}_{=0}\,\tcol{t}+\vec x_0\times \vec k \end{align} をすれば$\tcol{t}$が消える。

　第1の内積を使う方法を使ったならば、$\vec k_\bot=\mtx[c]{a\\ b}$で$\vec k_\bot\vec x_0=c$とすれば \begin{align} \goverbrace{a\xcol{x}+b\ycol{y}}^{\vec k_\bot\cdot\vec x}=\goverbrace{c}^{\vec k_\bot\cdot\vec x_0}\label{axbckbot} \end{align} が出てくる。

　第2の外積を使う方法を使ったならば$\vec k=\mtx[c]{-b\\ a}$}で$\vec x_0\times \vec k=c$とすれば \begin{align} \goverbrace{a\xcol{x}+b\ycol{y}}^{\vec x\times\vec k}=\goverbrace{c}^{\vec x_0\times\vec k}\label{axbck} \end{align} が出てくる。

　つまり、直線の方程式$a\xcol{x}+b\ycol{y}=c$の左辺は、ベクトル$\mtx[c]{a\\b}$とベクトル$\mtx[c]{\xcol{x}\\ \ycol{y}}$の内積だったと考えることもできるし、ベクトル$\mtx[c]{-b\\a}$と$\mtx[c]{\xcol{x}\\\ycol{y}}$との外積だったのだと考えることもできる。

　方向ベクトル$\vec k$と垂直なベクトル$\vec k_\bot$（今の場合$\mtx[c]{a\\b}$であった）をこの直線の「法線ベクトル(normal vector)」垂直を表す「normal」は「普通」と混同しそうだが、そういう言葉を使うことになっているので仕方ない。と呼ぶ。$\vec k_\bot=\mtx[c]{a\\b}$とすると、これと直交するベクトルの一例は$\vec k=\mtx[c]{-b\\a}$である。

　この式は、内積の分配法則を使って \begin{align} \vec k_\bot\cdot(\vec x-\vec x_0)=0\label{naisekisen} \end{align} と書き直すことができる。この式は「$\vec k_\bot$と$\vec x-\vec x_0$の内積が0である（すなわちこの二つのベクトルが直交する）」と述べていることになる。

　方向ベクトルが$\mtx[c]{-b\\a}$であることを求めるには、2次元のベクトルである$\mtx[c]{a\\ b}$をあえて3次元ベクトル$\mtx[c]{a\\[-1mm]b\\[-1mm]0}$にして、$\mtx[c]{0\\[-1mm]0\\[-1mm]1}$と外積を取るという方法もある。 \begin{align} \mtx[c]{0\\0\\1} \times\mtx[c]{a\\b\\0} =\mtx[c]{-b\\ a\\0} \end{align} である。なお、ここで外積の順番を逆にするとできあがる法線ベクトルは$\mtx[c]{b\\-a}$になる。$-1$倍になっただけで、法線ベクトルであるという性質は変わらない。

線分とベクトル

　位置ベクトルが$\vec x_0,\vec x_1$である2点を通る線分（直線ではなく）上の点は \begin{align} \xcol{\vec x}=(1-\tcol{t})\vec x_0 + \tcol{t}\vec x_1 \end{align} と表現できる。方向ベクトルが$\vec k=\vec x_1-\vec x_0$になっていると考えることもできる。$\tcol{t}=0$なら$\xcol{\vec x}=\vec x_0$、$\tcol{t}=1$なら$\xcol{\vec x}=\vec x_1$であることはすぐわかる。$\tcol{t}$がすべての実数であればこの式は直線を表すが、$0\le\tcol{t}\le1$の範囲に限ることにより「位置ベクトルが$\vec x_0,\vec x_1$である2点を結ぶ線分上の点」を表している。

　2本の直線（$\xcol{\vec x}=\vec x_{01}+\vec v_1\tcol{t}$と$\ycol{\vec x}=\vec x_{02}+\vec v_2\scol{s}$）の交点を求めるには、この2式を連立方程式として解けばよい。成分でやるよりベクトル表示を使った方が見通しがいい。まず引き算を行って、 \begin{align} \vec 0=\vec x_{01}-\vec x_{02}+\vec v_1\tcol{t}-\vec v_2\scol{s} \end{align} とする。パラメータ$\tcol{t}$と$\scol{s}$を求めたいから、上の式と$\vec v_1,\vec v_2$との外積をそれぞれ取って \begin{align} 0&=\vec v_1\times (\vec x_{01}-\vec x_{02})-\vec v_1\times \vec v_2\scol{s}\\ 0&=\vec v_2\times (\vec x_{01}-\vec x_{02})+\vec v_2\times \vec v_1\tcol{t} \end{align} となる。$\vec v_1\times\vec v_2=0$だと困ったことになるこうなるのは2直線が平行なときなので、交点が求まらなくなって困るのは当然である。が、そうではないとすればこれで$\tcol{t},\scol{s}$が決まる。これから決まる$\tcol{t}={\vec v_2\times (\vec x_{01}-\vec x_{02})\over \vec v_2\times \vec v_1},\scol{s}={\vec v_1\times (\vec x_{01}-\vec x_{02})\over \vec v_1\times \vec v_2}$を元の式に代入した結果 \begin{align} {\vec x} =\vec x_{10}+\vec v_1{\vec v_2\times (\vec x_{01}-\vec x_{02})\over \vec v_2\times \vec v_1} =\vec x_{20}+\vec v_2{\vec v_1\times (\vec x_{01}-\vec x_{02})\over \vec v_1\times \vec v_2}\label{koutents} \end{align} が交点の位置ベクトルである。

三角形とベクトル

　位置ベクトルが$\vec r_1=\mtx[c]{x_1\\y_1},\vec r_2=\mtx[c]{x_2\\y_2},\vec r_3=\mtx[c]{x_3\\y_3}$である三つの点を頂点とする三角形について考えていこう。

　3つの辺は

のように、 \begin{align} \xcol{\vec a}&=\vec r_2-\vec r_1=\mtx[c]{x_2-x_1\\y_2-y_1},\\ \ycol{\vec b}&=\vec r_3-\vec r_2=\mtx[c]{x_3-x_2\\y_3-y_2},\\ \zcol{\vec c}&=\vec r_1-\vec r_3=\mtx[c]{x_1-x_3\\y_1-y_3} \end{align} の3本のベクトルで表現されることになる。このとき、 \begin{align} \xcol{\vec a}+\ycol{\vec b}+\zcol{\vec c}=0 \end{align} が成り立つことに注意せよ。

のように「辺$\xcol{a}$と辺$\ycol{b}$の境界である頂点から、辺$\zcol{c}$を見る角度」を$C$と表現することにする（角度$A,B$も同様）。

　角度Cの$\sin,\cos$に関して \begin{align} \xcol{\vec a}\times \ycol{\vec b}&=\xcol{a}\ycol{b}\sin\left(\pi-C\right)=\xcol{a}\ycol{b}\sin C\\ \xcol{\vec a}\cdot\ycol{\vec b}&=\xcol{a}\ycol{b}\cos\left(\pi-C\right)=-\xcol{a}\ycol{b}\cos C \end{align} が成り立つ（これも、角度$A,B$についても同様）。

　三角形の面積は、外積を使うと \begin{align} S={1\over 2}\left|\xcol{\vec a}\times \ycol{\vec b}\right|={1\over 2}\left|\ycol{\vec b}\times \zcol{\vec c}\right|={1\over 2}\left|\zcol{\vec c}\times \xcol{\vec a}\right|\label{threeS} \end{align} のように3通りの方法で表現することができる。この三つの表現が等しいことは、 \begin{align} \xcol{\vec a}\times \ycol{\vec b} = \xcol{\vec a}\times(-\zcol{\vec c}-\xcol{\vec a}) =-\xcol{\vec a}\times \zcol{\vec c} -\underbrace{\xcol{\vec a}\times \xcol{\vec a}}_{\vec 0}=\zcol{\vec c}\times \xcol{\vec a} \end{align} のように外積の性質から証明できる。また、\式{threeS}を$\xcol{a}\ycol{b}\zcol{c}$で割ると、 \begin{align} {S\over\xcol{a}\ycol{b}\zcol{c}} =&{1\over 2\xcol{a}\ycol{b}\zcol{c}}\left|\xcol{\vec a}\times \ycol{\vec b}\right|={1\over 2\xcol{a}\ycol{b}\zcol{c}}\left|\ycol{\vec b}\times \zcol{\vec c}\right|={1\over 2\xcol{a}\ycol{b}\zcol{c}}\left|\zcol{\vec c}\times \xcol{\vec a}\right|\nonumber\\ =&{1\over 2\zcol{c}}\sin C={1\over 2\xcol{a}}\sin A={1\over 2\ycol{b}}\sin B\label{seigen} \end{align} となって、これから正弦定理 \begin{align} {\sin C\over \zcol{c}}={\sin A\over \xcol{a}}={\sin B\over \ycol{b}} \end{align} が得られる。

　余弦定理の方は、 \begin{align} \zcol{c}^2=&\zcol{\vec c}\cdot\zcol{\vec c} =(\xcol{\vec a}+\ycol{\vec b})\cdot(\xcol{\vec a}+\ycol{\vec b}) =\xcol{\vec a}\cdot\xcol{\vec a} +2\gunderbrace{\xcol{\vec a}\cdot\ycol{\vec b}}_{\xcol{a}\ycol{b}\cos\left(\pi-C\right)} +\ycol{\vec b}\cdot\ycol{\vec b} =\xcol{a}^2+\ycol{b}^2-2\xcol{a}\ycol{b}\cos C \end{align} のようにして内積の式から導くことができる。

円とベクトル

　円周上の一点の位置ベクトルを$\xcol{\vec x}$、円の中心の位置ベクトルを$\vec c$とすると、 \begin{align} \left|\xcol{\vec x}-\vec c\right|=R \end{align} あるいは \begin{align} \left(\xcol{\vec x}-\vec c\right) \cdot \left(\xcol{\vec x}-\vec c\right) =R^2 \end{align} がその満たすべき方程式である。

　中心$\vec c$から、距離$R$移動したとする。その移動の変位を$\vec R_1$とすれば、その点の位置ベクトルは$\vec c+\vec R_1$である。円の反対側の点は$\vec c-\vec R_1$と書くことができるが、その点も当然、円周上にある。以下の方程式が成り立つことはすぐに示すことができる。 \begin{align} \left(\xcol{\vec x}-(\vec c+\vec R_1)\right) \cdot \left(\xcol{\vec x}-(\vec c-\vec R_1)\right) =0\label{enchokkaku} \end{align}

　これを示すには、スカラーに対してよく使う$(a+b)(a-b)=a^2-b^2$のベクトル版である$(\vec a+\vec b)\cdot(\vec a-\vec b)=\vec a\cdot \vec a-\vec b\cdot \vec b$を使えばよい（証明はすぐできる）。

　内積ではなく外積だと、$(\vec a+\vec b)\times(\vec a-\vec b)=\vec a\times \vec a-\vec b\times\vec b$とはならず、$(\vec a+\vec b)\times(\vec a-\vec b)=2\vec b\times\vec a$となる。これも証明はすぐできる。

　この式の幾何学的意味は「$\xcol{\vec x}-(\vec c+\vec R_1)$と$\xcol{\vec x}-(\vec c-\vec R_1)$は直交する」ということで、これは確かに図を描くと「直径に対する円周角は直角$\left({\pi\over 2}\right)$である」ということだと納得できる。幾何学的に出てくる関係式を、ベクトルの式からも出すことができる。ここで、ベクトルで計算するときに、成分一個一個を計算する必要は全くない（たとえば$\vec c$と表現すれば、その$x$座標と$y$座標を両方書いて計算する必要はないのである）という点が重要で、ベクトルで表したときの大きな御利益である。

その他の内積・外積に関する式 3次元空間の図形と内積・外積

3次元空間の図形と内積・外積

　2次元空間の直線は前項の通りだが、3次元では、方向ベクトルを使った方の表現は、そのまま成分を三つに増やせばよく、 \begin{align} \gunderbrace{\mtx[c]{\xcol{x}\\ \ycol{y}\\ \zcol{z}}}_{\vec x} =\mtx[c]{k_x\tcol{t}+x_0\\ k_y\tcol{t}+y_0 \\ k_z\tcol{t}+z_0} =\gunderbrace{\mtx[c]{k_x\\k_y\\k_z}}_{\vec k}\tcol{t}+\gunderbrace{\mtx[c]{x_0\\y_0 \\z_0}}_{\vec x_0} \end{align} となる。しかし、法線ベクトルを使った表現ではうまく行かない。3次元では「あるベクトルに垂直である点を通る直線」を決めても一つに決まらないからである。3次元で「法線ベクトルと通る点を一つ決めると決まる」のは、次に述べる平面である。

　3次元内で「直線」を指定するには二つの条件がいる。上の式は$\vec x-\vec x_0=\vec k\tcol{t}$という式になるから、これから$t$を消すなら、 \begin{align} \tcol{t}={x-x_0\over k_x}={y-y_0\over k_y} ={z-z_0\over k_z} \end{align} のように$\tcol{t}$を求める式を作ることになる。これがよく使われる3次元での直線の式である。$\tcol{t}$は消してしまったので、この式は2本の等式である。3次元空間で2本の式による制約を加えたので、残る次元は1になる（つまり線）。

3次元空間内の面

　既に述べたように、3次元空間で1の条件だけをつけたのでは、結果は面（2次元の存在）になる。3次元空間内で法線ベクトル$\vec n=\mtx[c]{a\\b\\c}$をもち、ある一点$\vec x_0=\mtx[c]{x_0\\ y_0 \\ z_0}$を通る平面の方程式は \begin{align} \mtx[ccc]{a&b&c}\mtx[c]{\xcol{x}-x_0\\ \ycol{y}-y_0\\ \zcol{z}-z_0}=&0\\ \vec n\cdot(\vec x-\vec x_0)=&0\\ a\xcol{x}+b\ycol{y}+c\zcol{z}=&\gunderbrace{ax_0+by_0+cz_0}_{d} \end{align} である（上の式はみな同じ意味である）。

　なお、やはり一つだけの条件をつけた、 \begin{align} |\vec x-\vec x_0|^2 =(\vec x-\vec x_0)\cdot(\vec x-\vec x_0)=R^2 \end{align} は（円ではなく）球面になる。

　なお、webClassに情報を載せていますが、授業があった日の午後7時より約１時間、オンラインオフィスアワーとしてzoomを開いてます。質問や相談などがある人は来て話してください。

平面図形と内積・外積 受講者の感想・コメント

受講者の感想・コメント

　webclassでのアンケートによる、感想・コメントなどをここに記します。

　青字は受講者からの声、赤字は前野よりの返答です。

　主なもの、代表的なもののみについて記し、回答しています。

外積に関する定理など